考虑艇体变形影响的轴系合理校中
毛卫
海军装备部,北京 100841
0 引言
准确计算由于潜器的艇体变形所引起的轴承变位[1]并采用合理的校中方法,对提高潜器轴系校中的质量意义重大。
合理校中,即将轴系按照轴承载荷合理分配的原则确定轴承跨距、标高等轴系布置参数,该状态下的轴系运行更加稳定。该方法被水面船舶轴系校中广泛采用[2],并考虑了艇体变形的影响[3-5];但目前潜器的轴系校中采用的仍然是传统的直线校中方式,而且未考虑艇体变形对轴系校中的影响,由此带来如下一些问题:
1)直线校中是将轴承座看作刚体,不考虑轴承座的变形和轴承载荷的合理分配,仅通过控制轴段法兰的偏移和曲折来安装轴系,在使用过程中容易导致轴承磨损加剧、轴系振动增加[6]。
2)未考虑艇体变形对轴系校中的影响,使得轴系在实际运行过程中的校中状态与计算校核状态不一致,轴系实际的运行状态不可控。在工程实际中,艇体受支撑状态、装载状态、深水压力和环境温度等众多因素的影响,会导致艇体变形,造成轴承变位,改变轴系校中的状态。传统的直线对中安装方式已不能满足潜器轴系的使用要求,必须采用考虑艇体变形的合理校中。
目前,计算轴承变位的普遍方法是在轴系区域内对艇体模型进行简化处理,将耐压壳体简化为圆柱体和圆锥体[7]进行简单的估算,但其结果的准确性不能满足开展精确轴系校中设计的要求,必须研究一种能准确计算轴承变位的方法。本文将通过建立整艇有限元模型,计算潜器在满载、极限工作水深状态下,在重力和静水压力共同作用下艇体的变形情况。为使计算结果更加准确,将在计算中使艇体处于正浮状态,并在重心处施加固支边界条件。同时,本研究还将提出“共线程度”的概念,由此通过艇在水下的结构变形计算结果获得轴承支点处的变位值。通过将艇体变形导致的轴承变位作为校中计算的边界条件,并利用有限元法,以各轴承载荷合理分配为目标,开展轴承布置优化计算,可以实现考虑艇体变形影响的轴系合理校中计算。
艇体变形对轴系校中影响较大、合理校中计算方式更加合理[8-10],这是共识,因此,本文的重点不是去讨论考虑与不考虑艇体变形校中结果的差异、直线校中与合理校中的差异,而是针对现在潜器轴系校中存在的问题,研究准确计算轴承相对变位的方法,实现计及艇体变形的轴系合理校中,以为工程实践提供技术参考。
1 模型
1.1 轴系模型
某试验潜器推进轴系由推力轴、推力中间轴和艉轴连接而成,校中模型如图1所示。图中:表示轴系各轴承;↓表示集中质量,包括螺旋桨、弹性联轴器;↑表示轴承反力。
1.2 艇体有限元模型
模型潜器基本结构由耐压艇体、内部舱壁、浮筏基座、内部上层甲板和艉部结构等组成,整个结构总体上是由板、加强筋拼装而成,因此在进行有限元建模时,基本结构各部分采用板单元和梁单元模拟。
对于模型潜器上的设备,按最大程度接近设备实际工作状态进行简化的原则建模。
模型潜器基本结构和系统有限元模型如图2所示。

图1 模型潜器推进轴系模型Fig.1 Propulsion shafting model of a submersible vehicle

图2 模型潜器有限元模型Fig.2 FE model of a submersible vehicle
2 艇体变形计算及分析
2.1 边界条件
利用三维有限元计算方法计算模型艇满载、极限工作水深状态下的艇体变形。考虑重力和静水压力的作用,忽略温度变化引起的载荷,潜器艇体结构的受力情况如图3所示。

图3 模型艇受力图Fig.3 Sketch of load distribution
为消除由于计算误差等原因造成的刚体位移,影响计算结果的准确性,在整艇的重心处施加固定约束,如图4所示。

图4 重心处施加固定约束示意图Fig.4 Sketch of a fixed constraint at the center of gravity
经计算,固定点约束反力如表1所示。

表1 固定点约束反力Tab.1 Constraint reactions at fixed point
2.2 艇体艉部变形计算
通过整艇变形的计算,得到艉部4个轴承处艇体结构相对变形,从而为轴系校中计算提供轴承的相对变位。艉部4个轴承的位置以及与轴承相连的轴承套管、基座等的结构如图5所示,轴承对轴的作用力则使用相当刚度的三向弹簧来模拟,支撑点分别在艇体结构节点1~4处。
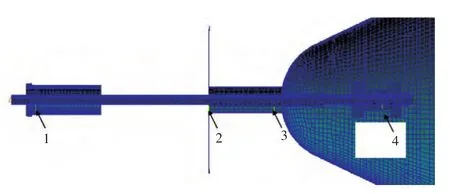
图5 艉部4个轴承的位置图Fig.5 Position sketch of the four bearings
利用三维有限元计算软件,计算整艇湿表面结构在上述边界条件下的垂向静态变形情况,计算时,将艇的重心位置设定为固定约束,艇体表面采用均布载荷,考虑重力的影响。计算结果如图6所示。

图6 整艇湿表面结构垂向变形图Fig.6 Sketch of whole hull wet surface static deformation in vertical direction
艉部4个轴承的位置以及与轴承相连的轴承套管、基座等结构垂向变形的有限元计算结果如图7所示。

图7 轴承处结构垂向变形图Fig.7 Vertical deformation of the structures connected to bearings
4个轴承处艇体结构垂向位移随着距艇体最艉端距离的不同其变化趋势如图8中的粗实线所示。由图8可以看出,4个轴承处艇体结构的垂向位移均较大,相邻各点的位移变化也较大,但是,这些量是在研究整艇的刚度等问题时所关心的。研究轴系校中问题,关心的是各轴承支撑点的相对共线程度,是一种相对量,以轴系中任意两个相邻轴承的连线为基准线,确定轴系各轴承相对基准线的位移,即为各轴承之间的共线程度的定量表示,此数据同时作为轴承变位值代入轴系校中计算中。为说明如何得到该相对量,在图8粗实线的基础上,作如下辅助图,如图8中的细实线所示。首先,过A点(对应节点4)和B点(对应节点3)作直线,以过AB的直线为基准线,然后,过C点(对应节点2)和D点(对应节点1)向直线AB作垂线段。由于艇体为小变形,轴承支点所在平面做平断面转动,那么这两个垂线段的长度就是所要的相对量,也是轴系校中计算所需要的相对变形量。
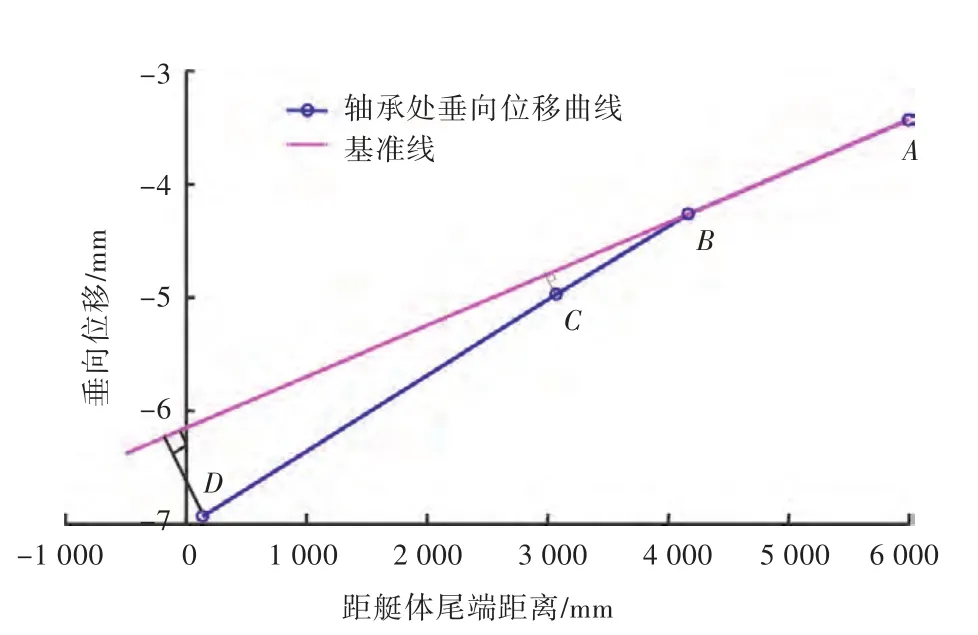
图8 艉部4个轴承处艇体结构垂向位移相对量图Fig.8 Vertical relative displacements of the structures at stern bearings
根据图8,得到艉部4个轴承处艇体结构垂向位移的相对量,如表2所示。

表2 艉部4个轴承处艇体结构垂向位移的相对量Tab.2 Vertical relative displacement of the structures at stern bearings
3 计入艇体变形的轴系校中
合理校中计算的过程是一种优化计算的过程,以使支撑螺旋桨的艉管后轴承的轴承负荷最小作为优化目标,以各轴承的负荷允许范围、轴段弯曲应力允许范围以及艉管后轴承支撑点处截面转角允许范围作为优化约束条件。本文所用轴系合理校中的基本计算过程如下:
1)建立轴系有限元模型,获得质量、刚度以及外力等矩阵,确定各轴承的初始变位情况,形成轴系模型模块及轴系校中计算模块;
2)利用优化算法对轴承变位情况进行样本选择,反复调用轴系校中计算模块,直至满足约束条件并达到目标函数的结果出现,即获得轴系合理校中计算的结果。
合理校中优化计算的约束条件如下:
1)橡胶轴承的允许比压不大于0.3 MPa;
2)油润滑金属轴承的允许比压不大于0.8 MPa;
3)每个轴承均为正反力,且均大于相邻两跨轴重量(G)的20%;
4)螺旋桨轴、艉轴和中间轴附加弯曲应力不大于20 MPa;
5)在艉管后轴承支点处,轴段转角不大于3.5×10-4rad。
目前常用的轴系校中计算是将轴承支撑看作刚性支撑,未考虑轴承的径向支撑刚度。在本文的轴系校中计算模块中,是将轴承视为弹性支撑,根据轴承的类型及结构赋予合适的刚度值。合理校中计算的内容有:
1)轴承合理变位的确定;
2)轴承受力状态计算及各截面处的弯矩、剪力、转角、挠度等;
3)弹性曲线;
4)轴承负荷影响系数。
3.1 基本参数
水润滑艉轴承下4点支撑,轴承支点取L/4(L为轴承长度),校中计算计入艇体变形和轴承刚度。轴承的基本参数如表3所示,轴承单元属性如表4所示,外载荷和轴承负荷影响系数分别如表5和表6所示。
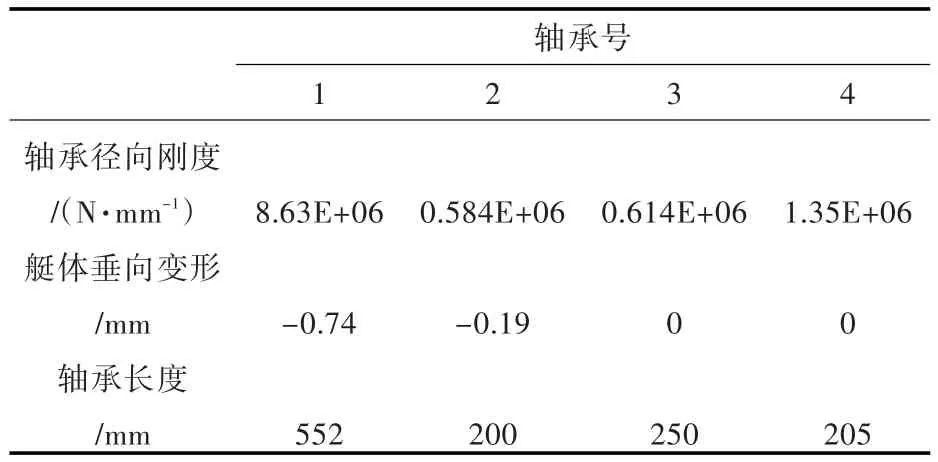
表3 轴承基本参数Tab.3 Basic parameters of bearings

表4 轴系的单元属性Tab.4 Element attributes of the shafting

表5 轴系受到的外部载荷Tab.5 Outer loads on shafting
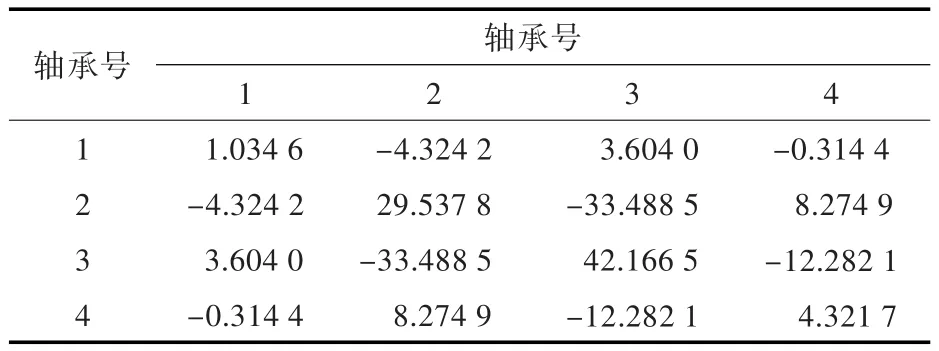
表6 轴承负荷影响系数Tab.6 Influence coefficients of bearing reaction
3.2 轴系安装状态下的校中计算(螺旋桨全浸水)
表7中,“G”表示该轴承左右两轴段间的外加载荷及自重之和,轴承支反力之和是23.79 kN,表中轴承挠度为考虑艇体变形和轴承刚度后的实际挠度。安装时,1#、2#、3#轴承位于理论中心线上,4#轴承变位为理论中心线向上0.4 mm。轴承状态计算结果如表7所示。
在水润滑艉轴承下4点支撑这种情况时:
1)轴承的负荷小于轴承的允许比压;

表7 法兰连接时轴承状态Tab.7 Bearing status when flange in connecting condition
2)每个轴承均为正反力,且均大于相邻两跨轴重量(G)的20%;
3)螺旋桨轴(艉管轴)最大附加弯曲应力为7.467 MPa;
4)中间轴最大附加弯曲应力为1.160 MPa;
5)在艉管后轴承支点处,艉轴与艉管后轴承的相对倾角为-2.933×10-4rad。
从表7中两组支反力计算结果可以看出,采用直线校中安装的轴系,2#轴承载荷偏小,不满足支反力不小于相邻轴段重量20%的要求,通过考虑艇体变形及轴承刚度的合理校中,使所有轴承载荷均满足合理要求。
弹性曲线/弯矩曲线图(考虑艇体变形和轴承刚度)如图9所示。
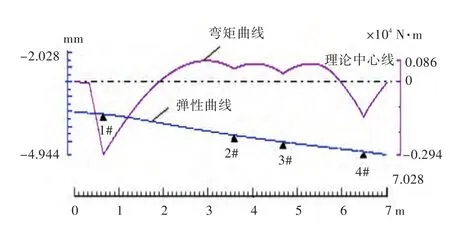
图9 轴系校中弹性曲线Fig.9 Elastic curve and bending moment curve of shafting alignment
4 结 论
1)潜器在满载、极限工作深度条件下,艇体结构变形成“拱形”,即距离艇体重心越远,垂向位移越大。
2)本文提出了“共线程度”的概念,将艇体结构变形计算结果转化为轴承相对变位数据,获得了艇体变形对轴承变位的影响。
3)轴系校中计算结果表明,考虑艇体变形和轴承刚度的合理校中方法能够保证轴系校中状态参数均在合理范围内,而直线校中状态安装的轴系会存在某一个轴承载荷偏小的问题。
[1]American Bureau of Shipping.Guidance notes on propulsion shafting alignment[R].Houston,2006.
[2]周瑞平.超大型船舶推进轴系校中理论[D].武汉:武汉理工大学,2005.
[3]耿厚才,郑双燕,陈建平.大型船舶船体变形对轴系校中的影响分析[J].船舶工程,2010,32(5):7-9.GENG Houcai,ZHENG Shuangyan,CHEN Jianping.Influence analysis of large vessel hull deformation on shafting alignment[J].Ship Engineering,2010,32(5):7-9.
[4]MURAWSKI L.Shaft line alignment analysis taking ship construction flexibility and deformations into consideration[J].Marine Structures,2005,18(1):62-84.
[5]LOW K H,LIM S H.Propusion shaft alignment method and analysis for surface crafts[J].Advances in Engineering Software,2004,35(1):45-58.
[6]石磊,薛冬新,宋希庚.计入船体变形影响的轴系动态校中研究[J].大连理工大学学报,2011,51(3):375-380.SHI Lei,XUE Dongxin,SONG Xigeng.Study of dynamic shafting alignment considering ship hull deformations[J].Journal of Dalian University of Technology,2011,51(3):375-380.
[7]俞强,郭全丽.潜器轴系校中计算研究[J].船海工程,2003(6):32-34.YU Qiang,GUO Quanli.On alignment calculation of the submersible shafting[J].Ship&Ocean Engineering,2003(6):32-34.
[8]王贤峰,周继良.船舶推进轴系动态校中与仿真研究[J].船舶工程,1996(4):25-29.WANG Xianfeng,ZHOU Jiliang.Simulation of dynamic alignment for marine propulsion shafting[J].Ship Engineering,1996(4):25-29.
[9]耿厚才.船舶轴系的动态校中计算[J].中国造船2006,47(3):51-56.GENG Houcai.Dynamic alignment calculations for marine shafting[J].Shipbuliding of China,2006,47(9)51-56.
[10]徐立.船舶轴系合理校中的最优化设计[J].船海工程,2001(4):36-38.XU Li.Optimum design for rational aligning of the ship's shaft system[J].Ship&Ocean Engineering,2001(4):36-38.

