基于改进的接触爆炸毁伤模型的航空母舰不沉性评估
张凯,胡玉龙,熊治国,王健,赵永振,朱旭
1 海军驻上海地区舰炮系统军事代表室,上海 200136
2 中国舰船研究设计中心,湖北武汉 430064
0 引 言
在航空母舰的方案设计阶段进行不沉性评估是该阶段生命力设计与控制的重要内容。传统的不沉性评估主要是在指定破舱组合下,要求其满足确定性校核规范的要求[1-2];但这种不沉性校核方式中指定破舱组合的方法没有正确地反应航空母舰遭受武器毁伤下的破舱特性,也没有考虑多发武器命中下的破舱特性,而且,确定性的校核手段也不能对航空母舰毁伤后的生存能力给出定量评价指标,已经不能满足现代舰船生命力设计和评估的要求。针对上述问题,本文拟研究开发航空母舰遭受单发和双发武器命中时的舱室毁伤模型,并在此基础上分析双发毁伤位置变化对航空母舰浮态的影响;最后,从满足不沉性校核规范和考虑动态海浪环境对破损航空母舰的不利影响两方面建立毁伤后航空母舰的残存概率模型。该方法将可作为航空母舰方案设计阶段不沉性设计与评估的方法和手段。
1 接触爆炸毁伤模型
1.1 结构毁伤模型
军舰的毁伤分接触爆炸毁伤和非接触爆炸毁伤2种。接触爆炸毁伤是指航空母舰在执行任务的过程中遭受来自水下和空中武器的直接命中而发生局部结构的破坏,从而导致舱室进水、倾斜或沉没;非接触爆炸毁伤主要指武器在舰船附近水中爆炸产生的冲击波和气泡脉动等的联合作用使船体产生振荡而发生的总体结构的破坏[3]。就航空母舰总是以战斗编队形式执行任务的特点来看,其主要威胁来自各种反舰导弹和制导鱼雷,它们对航空母舰的破坏主要以接触毁伤为主。本文将上述武器对航空母舰的攻击在船体中纵剖面图中简化为了毁伤半径为r0、圆心坐标为(x0,z0)的圆形靶区(图 1),并记为毁伤参数(x0,z0,r0,index),其中,index=1表示毁伤在舰右舷,index=0表示毁伤在舰左舷。根据圆形靶区范围和水密横舱壁以及甲板的分布,可以得到由毁伤造成的毁伤区域,该毁伤区域实际上是由靶区外且离靶区最近的边界(水密横舱壁和甲板)围成的几何区域,该几何区域由一系列区域甲板构成,这里的区域甲板是指由水密横舱壁与甲板分割形成的空间区域,如图1所示。
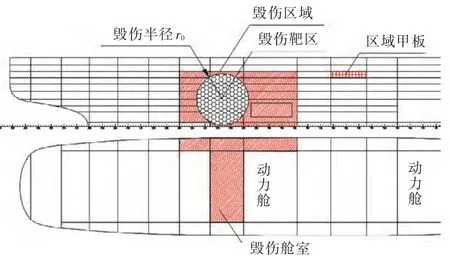
图1 舱室毁伤模型Fig.1 Damaged model of cabins
在中纵剖面视图上,首先通过干涉算法判断毁伤区域内每一个区域甲板是否与圆形靶区有重叠来判断该区域甲板是否毁伤。由于部分区域甲板内有左、右主纵舱壁,区域甲板被分成左、右边舱及中舱,因此,若毁伤区爆心(x0,z0)在区域甲板内,则该区域甲板爆炸一侧的边舱和中舱均破损,若爆心(x0,z0)不在该区域甲板内,则只有爆炸一侧的边舱破损;若区域甲板内不存在左、右主纵舱壁,则该区域甲板将完全破损进水。
在给定船型参数和毁伤参数下,需要自动甄别破损舱室并计算其几何要素;由于呆木、球鼻艏、大外飘,等使得航空母舰结构复杂,从而导致航空母舰一部分舱室的几何构型也十分复杂,不利于舱室数据的提取。根据舱室在中纵剖面投影的形状,本文将舱室按照几何构型分成了6类,如图2所示。图中i和 j分别表示甲板和水密横舱壁的索引值,是通过判断舱室两端横剖线的最低点的z坐标与i和 j甲板高度的关系来划分。第1类舱室由甲板和横舱壁交叉分割形成,绝大多数的舱室属于第1类;剩余的5类舱室是由水密横舱壁、甲板和呆木(或艏部外飘)共同分隔形成,舱室各剖面的型值数据读取方式各不相同,其中第6类未形成舱室,没有型剖面数据。需要指出的是,当航空母舰的动力舱处于毁伤区域时,由于航空母舰的动力舱尺寸比一般舱室大,特别是在垂直方向上贯穿多层甲板,因此,就需要重新修正动力舱室的型剖面数据,将动力舱处理为高度方向上贯穿多层甲板的整体舱室。

图2 舱室几何构型分类Fig.2 Geometrical categories of cabins
1.2 双发接触爆炸毁伤
航空母舰及其编队执行作战任务时往往面对的是敌方制导武器的多批次饱和攻击,因此,应该考虑多发武器命中下的航空母舰易损性评估。而双发武器毁伤是航空母舰易损性评估中的典型评估环境,航空母舰遭受双发武器命中时,对破坏区域的甄别要分为2种情形:情形1是两发武器毁伤靶区相距较远,毁伤区域不发生干涉;情形2是双发毁伤靶区相隔较近,导致毁伤区域发生干涉,如图3所示。

图3 双发毁伤干涉示意图Fig.3 Scheme of interference between double hits
对于毁伤情形1,可以对两次毁伤导致的破损舱室的几何要素进行单独计算后累加得到;对于情形2,则需要对毁伤干涉区域内的舱室进行干涉甄别,以免重复计算。本文在编制程序时,对上述问题进行了如下处理:首先,判断双发所造成的毁伤区是否重叠,不重叠时,毁伤区舱室数据互不影响;当毁伤区有重叠时,在进行第2发毁伤区舱室的数据读取时要考虑该毁伤舱室所在区域甲板在第1发中是否毁伤,同时,还要考虑舱室所在区域甲板内是否有主纵舱壁、第1发爆心是否在该区域甲板、第2发的爆心是否在该区域甲板等条件,上述选择条件的组合决定了双发毁伤中第2发造成的破损舱室的数据。破损舱室数据读取流程图如图4所示。
2 毁伤对航空母舰浮态的影响
2.1 数学模型
根据静力学的相关知识,舰船漂浮在水面平衡的条件为:
1)舰船的重力G与浮力γV大小相等,即合力的主矢量T=0;
2)舰船的重力G与浮力γV的作用线在同一条铅垂线上,且方向相反,即合力的主矩M=0。
因此,舰船的平衡方程满足式(1)。

式中,Mx,My和 Mz分别表示力矩 M 在随船坐标系上的分量。对式(1)进行数学展开可得舰船破损(未破损)状态下的隐函数形式的平衡方程:


图4 双发毁伤破损舱室数据读取流程Fig.4 Flow chart of reading damage cabins data in double hits condition
式中,mxz,mxy和myz分别是关于破损(未破损)舰船几何要素的非线性函数。方程组(2)中,第1个方程为垂向平衡方程,第2个方程为横向平衡方程,第3个方程为纵向平衡方程。该方程组表示舰船平衡时的浮态参数(Tm,ϕ,θ)所确定的水线面应该满足的条件。其中:Tm为平均吃水;ϕ为横倾角;θ为纵倾角。
航空母舰破损稳性的计算采用“自由纵倾”时的最小稳性计算模型。即当航空母舰遭受毁伤后,平衡于浮态参数不为0(即 tan ϕ≠0,tan θ≠0)的水线面位置,在做等体积倾斜至某角度α时,该位置时的稳性计算转换为求该过程中舰船所做功的最小值,即
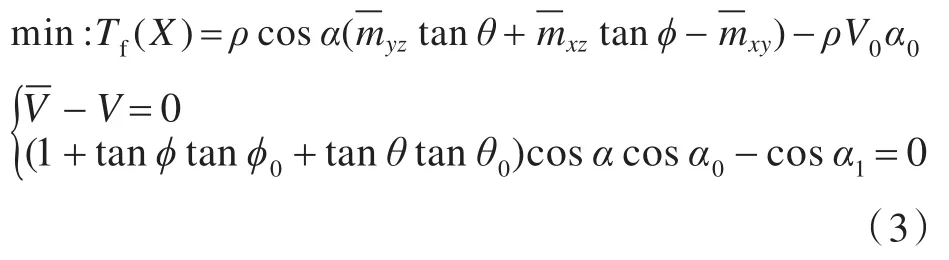
式中:设计变量 X=(Tm,tan ϕ,tan θ)为浮态参数;myz,mxz和mxy上的横线表示破损状态的相关函数;ρ为海水密度;V0为破损舰船稳定平衡时的排水体积;为舰船破损后横摇过程中的排水体积;V为舰船未破损时的排水体积;(ϕ0,θ0)为破损舰船稳定平衡时的横倾角和纵倾角;(ϕ,θ)为倾斜过程中舰船的横倾角和纵倾角,破损稳性数值计算过程中选取有限个离散点来计算;α0为平衡时的水线面倾角,且满足
α1为倾斜时水线面与平衡时水线面之间的夹角,由球面三角形几何关系,有

舰船破损后浮态与稳性的数值计算方法参见文献[4-6],本文不再赘述。
2.2 破损航空母舰与舱室几何要素计算
在求解航空母舰破损浮态和稳性过程中,需要分别计算船体和各个破损舱室在给定浮态参数下的水线面和水下体积几何要素,用以迭代求解非线性的浮态和稳性方程。本文中采用二维横剖线型来表达航空母舰的船型,会出现当水线面与船体的交线(交点)刚好在两个计算剖面之间时无法求解而导致计算精度较低的问题;文献[7-8]采用增加计算剖面数的方法来提高计算精度,但计算效率大大降低。针对这一问题,本文采用线性插值的方法先求出水线面与船体的交线(交点)的纵向坐标,然后使用该横剖线之前计算得到的数据点坐标,并利用样条插值的方法得到该临界位置处横剖线与水线面位置的交点,最后采用Green公式来计算破损舰船和破损舱室水线面和水下体积几何要素。图5为按照上述原理用程序计算得到的某浮态下破损航空母舰和破损舱段内的进水水线面示意图。
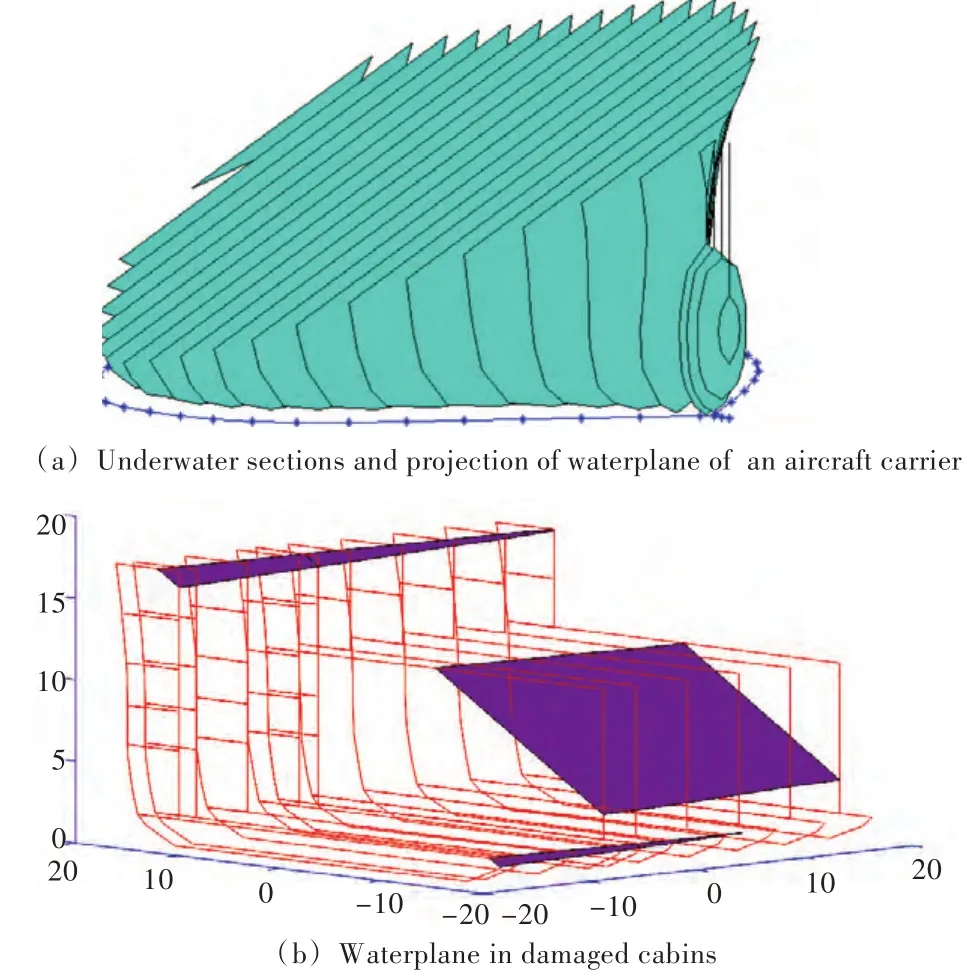
图5 破损舰船和舱室几何要素Fig.5 Geometrical characteristics of ship and cabins
其中:图5(a)为航空母舰在毁伤参数为(0,8,8,1)时发生破损进水稳定平衡后,航空母舰各横剖面水下部分以及水线面在绝对坐标系中的水平面上的投影示意图;图5(b)为随船坐标系下毁伤参数为(0,8,8,1)时破损舱段内破损舱室进水示意图,其中一部分舱室被海水完全充满,另一部分未被海水完全充满而存在自由液面,采用Green公式逐个计算破损舱室的进水体积和舱内水线面几何要素并累加得到航空母舰所有破损舱室的进水体积和水线面等几何要素。
2.3 双发毁伤对航空母舰浮态的影响
航空母舰作为大型主战舰艇,往往会遭受敌方武器的多批次饱和攻击;因此,研究航空母舰遭受多发武器毁伤具有重要意义。根据上述开发的航空母舰多发毁伤模型,本节将研究航空母舰在遭受双发武器接触爆炸毁伤下浮态的变化特性。双发毁伤采用第1发毁伤位置固定,第2发毁伤位置在全舰纵向和垂向变化时的仿真模型,并通过二维插值得到航空母舰浮态随第2发毁伤位置变化时的响应曲面。在两次双发毁伤仿真中,仿真1中的第1发毁伤参数(x0,z0,r0,index)为(100,8,8,1),即靶心在舰舯前部100 m,高度8 m;仿真2中第1发毁伤参数(x0,z0,r0,index)为(-100,8,8,1),即靶心在舰舯后部 100 m,高度8 m;两次仿真中的第2发毁伤位置在全舰变化时,得到航空母舰吃水增量、横倾角和纵倾角的响应曲面分别如图6~图8所示。在图6~图8中,浅色曲面为仿真1对应的响应曲面,深色曲面为仿真2对应的响应曲面。
图6为吃水增量的响应曲面。由图中可知,两次仿真中吃水增量的总体变化趋势基本一致,当第2发毁伤在船舯部、船舯部前后各50~60 m处时,仿真1和仿真2下的吃水增量同时达到最大;因此,从保证航空母舰不沉性的角度,需将舷侧防护区的长度至少涵盖到距船舯前后各50~60 m的危险区域。
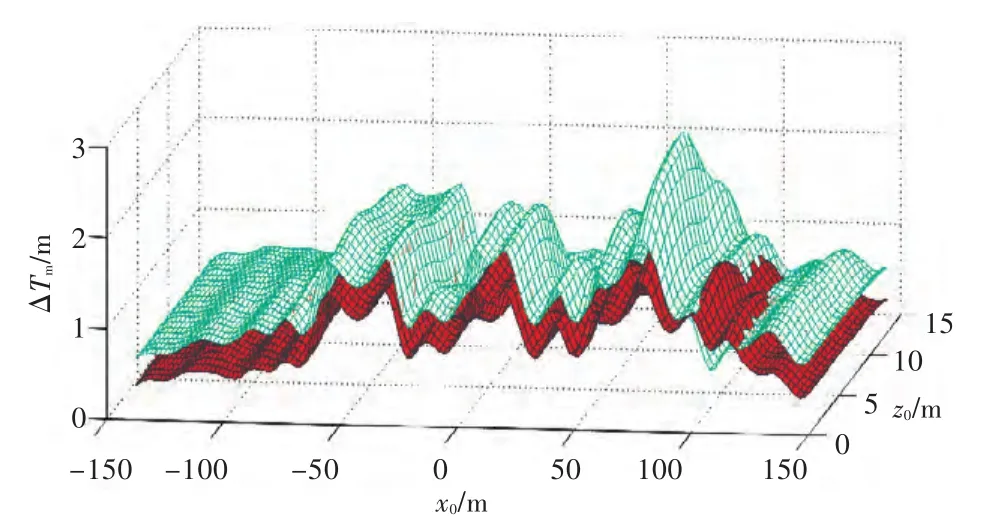
图6 吃水增量响应曲面Fig.6 Response surface of increased draft
图7为横倾角的响应曲面。由图可知,两种仿真模型下的横倾角变化趋势基本一致。当第2发毁伤在船舯部接近水线附近位置时,仿真2下的横倾角更显著;而当第2发毁伤不在船舯部位置时,仿真1下的横倾角更显著。当毁伤发生在动力舱所在区域时,两种仿真下的横倾都加剧,这主要是由于动力舱段沿纵向跨度较长,且高度方向贯穿多层甲板,从而导致破损大量进水的缘故。

图7 横倾角响应曲面Fig.7 Response surface of heeling angle
图8为纵倾角的响应曲面。当第2发毁伤在船舯以后区段时,仿真2下的纵倾角幅值更大;当第2发毁伤在船舯以前区段时,仿真1下的纵倾角幅值更大;在仿真1中,当第2发毁伤发生在船舯部前100 m处时(此时第1发毁伤与第2发毁伤在同一区域),纵倾角幅值最大达到1.5°左右;而在仿真2中,当双发毁伤发生在同一区域时,纵倾角没有恶化到该种程度。造成这种现象的原因是航空母舰艏部型线宽度收缩,导致区域甲板的宽度逐渐减小,且该收缩区的长度较大,导致在这部分区域甲板内没有设置主纵舱壁,因此当艏部发生毁伤时,区域甲板完全破损进水,特别是当双发毁伤发生在同一区域时,导致破损进水更为严重,从而加剧纵倾。

图8 纵倾角响应曲面Fig.8 Response surface of trimming angle
综合上述双发毁伤仿真对航空母舰浮态的影响分析,可以得到对航空母舰分舱和总布置设计的一些建议:
1)水线附近的舱室毁伤后对航空母舰浮态的影响比较大,应加强水线附近舱段的结构防护设计。
2)动力舱的设计应尽可能对称分布在船舯两端或靠近船舯部,并加强动力舱段的结构防护设计,防止毁伤大量进水造成较大的横/纵倾角,保持航空母舰的机动力。
3)在水线附近的高度范围内,特别是在舰舯前部,尽可能增大舷侧防护区的长度,以减小毁伤贯穿整个宽度范围内的舱段的概率。
4)航空母舰舯部毁伤后对舰的浮态影响较为严重,因此,对航空母舰舯部应尽可能加强防护设计。此外,尽可能不将易燃、易爆品舱室(燃油舱、弹药舱)布置在距航空母舰艏、艉部40 m区域范围内。
3 毁伤航空母舰的残存概率模型
目前,各国海军使用的破损稳性校核规范都是确定性的校核规范,无法对舰船抵御破损后稳性损失的能力给出定量评价,不能直接用于舰船方案的生命力定量评估。例如,美海军于上世纪70年代提出的DDS-079不沉性校核规范,对不同船长舰艇的破损长度和范围都做了定量的限制,同时对主要功能舱室的渗透率也做了进一步的规范要求[2],并给出了不同设计水线长度下舰船的破损浮态和动稳性校核准则。在动稳性方面,该规范是通过对破损稳性力臂—风倾力臂曲线上的面积A1与面积A2的比值大于或等于1.4来限定。目前,世界各国海军的舰船不沉性校核规范都是引用或以该规范为基础制定的;因此,本文以该规范作为研究的参考规范。根据本文所开发的武器毁伤不沉性计算程序,并按照DDS-079规范,得到毁伤参数为(0,6.5,7.5,1)时的稳性校核图,如图9所示。图中:C点为破损后的静平衡点,对应的横倾角ϕ=6.53°;D点为稳性力臂与风倾力臂的交点,并按照规范向后取25°角作为回复角至E点,D点和E点之间稳性力臂曲线与风倾力臂曲线之间所夹的面积为A2;D点沿横倾角轴正向至最大稳性力臂对应的横倾角处为B点,D点和B点之间稳性力臂曲线与风倾力臂曲线之间所夹的面积为A1;二者的面积之比A1/A2=3.43。通过仿真计算可知,该毁伤想定下的破损航空母舰满足DDS-079不沉性规范的要求。
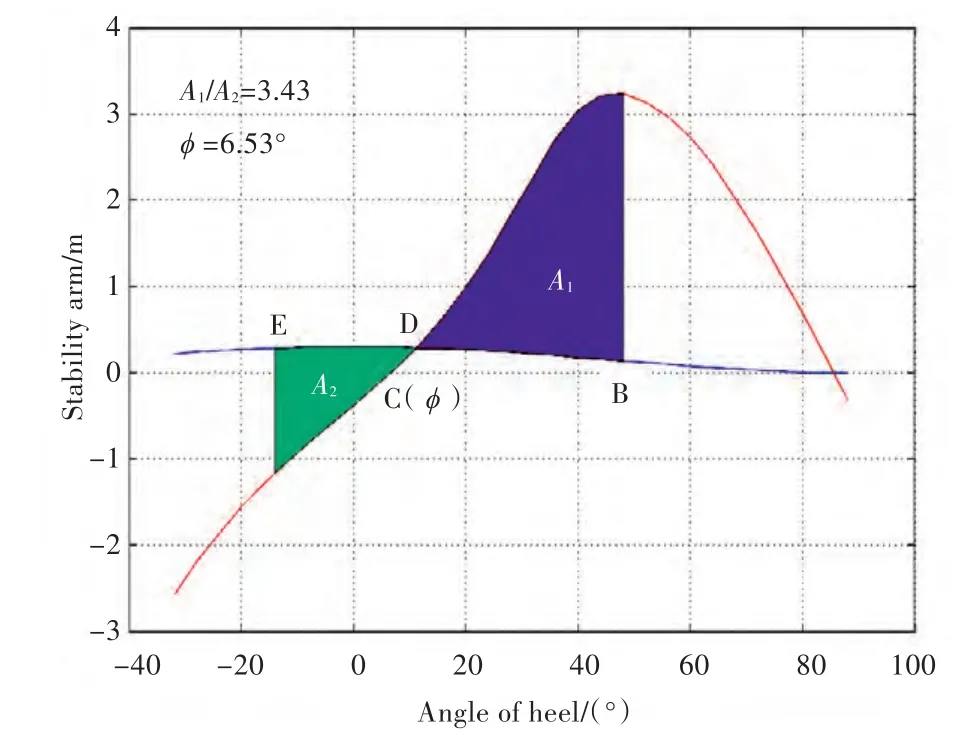
图9 破损稳性规范图解Fig.9 Figure of damage stability criteria
上述不沉性校核规范没有对航空母舰毁伤后的生存能力给出定量的评价,而且该规范的校核没有考虑海浪环境对破损舰船的影响。实际上,由于航空母舰遭受毁伤后破损区域较大,波浪的动态特性使得海水不断被抬高而注入破损舱室中是破损航空母舰在波浪中残存概率计算的主要考虑因素。研究人员采用了一种“准静态”的方法来研究波浪对破损航空母舰生存能力的影响[9-11],该方法认为船舶处于静稳定平衡后,由于波浪的动态特性使得海水被抬高进入破损舱内,当舱内进水达到某一临界质量时,船舶处于“无法回复”的临界状态,在该状态时船舶的稳性曲线刚好没有正的回复力臂。研究人员通过数值仿真和模型试验得出临界进水质量主要由舰船破损时所处海域的有义波高Hs决定的结论。因此,为了更客观地从稳性的角度来研究毁伤对航空母舰生命力的影响,不仅要考虑破损后航空母舰的稳性要满足军用规范的校核要求,还必须要求破损航空母舰能够有效抵御波浪的动态特性对不沉性的不利影响这一因素。目前,美、英等国的破损稳性校核规范都是建立在海况为有义波高Hs=8 ft(2.44 m)的基础上。当破损后航空母舰的稳性满足美国海军DDS-079破损稳性规范时,本文认为航空母舰的基础残存概率为作战海域内有义波高Hs满足Hs<8 ft时的概率,即此时基础残存概率为P0=P(Hs<8 ft);同时,为了考虑波浪动态特性的影响,需要考虑航空母舰机库大门位置离海面的高度。因此,用下式来表示从不沉性的角度评价毁伤后航空母舰的残存概率:

式中:D为机库甲板所在的高度;T'm为破损航空母舰的平均吃水;min F为破损航空母舰稳定平衡时相对于机库甲板高度的最小干舷;F0为安全储备(ft),且有 F0=0.1+0.5×(Hs(0.99)-8),其中Hs(0.99)表示海域中不超过某一有义波高的概率为0.99时对应的有义波高。本文建立的上述不沉性评估模型在满足现有不沉性军用规范的基础上,考虑了使用海况和航空母舰机库甲板这一结构特性对航空母舰毁伤后的影响,从而建立起对毁伤航空母舰生存能力的定量评价模型,满足航空母舰设计过程中不沉性多方案评估的需求。
根据上述基于武器毁伤的不沉性求解模型和残存概率模型,计算了7种毁伤工况下的浮态和残存概率,结果如表1所示。计算过程中,假定航行海区为西太平洋海域,其有义波高 Hs满足Hs<8 ft时的概率为0.85。计算结果中,第1种工况为图9所对应的毁伤参数时的浮态和残存概率;其余6种仿真工况中,3个为单发毁伤仿真,3个为双发毁伤仿真,且均为右舷毁伤。由计算结果可知,在所有毁伤参数下,航空母舰的不沉性均能满足确定性校核规范,同时在3次单发毁伤仿真中,航空母舰的残存概率在舯部毁伤时最低,在3次双发毁伤中,当舯部和艏部同时毁伤时其残存概率最低。

表1 计算结果Tab.1 Calculation results
4 结 语
本文针对航空母舰分舱方案设计过程中的不沉性评估问题,提出了基于接触爆炸毁伤的单发和双发舱室毁伤模型,能较好地模拟实际武器毁伤造成的破损舱组,克服了传统不沉性计算中指定破损舱组的方法;同时,为了解决传统不沉性确定性校核方法无法对航空母舰遭受毁伤后的生存能力给出定量评价的问题,提出了同时考虑规范校核和海浪对毁伤航空母舰不利影响等因素的残存概率模型,为航空母舰的易损性和生命力评估提供了参考手段。
[1]RIOLA J M,PÉREZ R.Warship damage stability criteria case study[J].Journal of Maritime Research,2009,6(3):75-100.
[2]SURKO S W.An assessment of current warship damaged stability criteria[J].Naval Engineers Journal,1994,106(3):120-131.
[3]LEE D,LEE S S,PARK B J,et al.A study on the framework for survivability assessment system of damaged ships[J].Ocean Engineering,2005,32(8):1122-1132.
[4]林焰,李铁骊,纪卓尚.破损船舶自由浮态计算[J].大连理工大学学报,2001,41(1):85-89.LIN Yan,LI Tieli,JI Zhuoshang.Ship damage floating calculation[J].Journal of Dalian University of Technology,2001,41(1):85-89.
[5]胡丽芬,马坤,张凤香.破损舰船浮态稳性实时计算研究[J].武汉理工大学学报:交通科学与工程版,2009,33(6):1160-1163,1182.HU Lifen,MA Kun,ZHANG Fengxiang.Study on real-time calculation of stability for damaged warship[J].Journal ofWuhan University of Technology:Transportation Science and Engineering,2009,33(6):1160-1163,1182.
[6]陈德志.船舶破损稳性计算方法研究[D].大连:大连理工大学,2004.
[7]张明霞.基于NURBS曲面的船舶破舱稳性计算方法研究[D].大连:大连理工大学,2002.
[8]陆丛红,林焰,纪卓尚.遗传算法在船舶自由浮态计算中的应用[J].上海交通大学学报,2005,39(5):701-705,710.LU Conghong,LIN Yan,JI Zhuoshang.Application of genetic algorithm in ship free floatation calculation[J].Journal of Shanghai Jiaotong University,2005,39(5):701-705,710.
[9]SANTOS T A,GUEDES S C.Numerical assessment of factors affecting the survivability of damaged ro-ro ships in waves[J].Ocean Engineering,2009,36(11):797-809.
[10]VASSALOS D,GUARÍN L.Designing for damage stability and survivability-contemporary developments and implementation[J].Ship Science and Technology,2009,3(5):59-72.
[11]PAPANIKOLAOU A,ELIOPOULOU E.On the development of the new harmonised damage stability regulations for dry cargo and passenger ships[J].Reliability Engineering and System Safety,2008,93(9):1305-1316.

