有限差分法求解薛定谔方程

宫建平

（晋中学院 信息技术与工程学院，山西晋中 030600）

0 引言

在量子力学中,对于一些简单的量子体系,如一维无限深势阱、线性谐振子、氢原子等体系的薛定谔方程可以严格求解,得到描述体系的精确的状态波函数和能量.但大多数量子体系的哈密顿算符都比较复杂,薛定谔方程一般得不到精确的解析解，有时能级可以给出解析表达式，但却无法得到波函数的解析表达式.因此,研究和发展薛定谔方程的计算方法就具有重要的意义.

由于有限差分法可以处理在几乎所有形式的势能函数中运动的粒子,并且因为计算主程序并不依赖于势能函数的具体形式，因此可以进行相对精确的计算,对于确定量子体系的束缚态能级和相应的波函数是一种非常有效的计算方法.近年来人们对有限差分法求解本征值问题进行了研究[1～2],但由于有限差分法求解的边界条件是假设计算区间的端点的波函数为零,这相当于在区间端点加上一无穷高的势垒,所以解总是存在的,但这里给出的解并不一定是原来给定势下的束缚态的解.本文对这一问题进行详细的讨论.

1 束缚态薛定谔方程的有限差分算法

根据有限差分法中的二阶微分中心差分算符可以将一维薛定谔方程写作

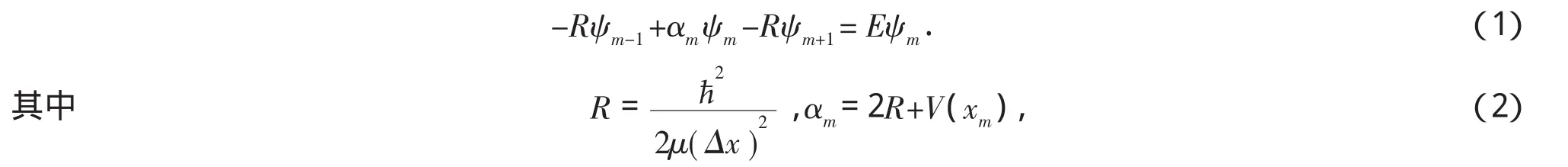
当取m=0，1，2，3，…，M.并且注意到满足条件 ψ0=ψM=0，则由（1）式得到一系列线性方程式，这样将本征值方程离散化为矩阵方程

我们将相对复杂的方程就转化为矩阵S的对角化问题,利用计算机数值计算可以容易将矩阵S的本征值和本征函数同时求出.

我们以线性谐振子为例讨论,线性谐振子的能量本征值方程为

为方便起见，引入无量纲变量ξ代替x，它们的关系是

薛定谔方程可改写为下面无量纲的形式

令,ψm=ψm(ξm)，ξm=ɑ+mΔξ，1≤m≤M，边界条件写成

实际上取ψ0=ψM=0（8）式得到一系列线性方程式

2 计算间隔的选择与波函数的归一化

在（10）式的计算中计算间隔直接影响本征值精度，并且发现计算间隔不同时所得的波函数曲线也会发生变化.图1是在区间[-5，]5内计算间隔分别取0.1，0.01，0.005时的波函数曲线，相应的能量本征值分别为0.4997ħω，0.5000ħω,0.5000ħω.如果要求精度精确到0.0001ħω，那么计算间隔取作0.01应该能够达到要求，因为在所要求的精度内，再减小计算间隔已经不再影响能量本征值的大小.

在图1中我们用点划线、虚线和点线绘制计算间隔为0.1、0.01和0.05时的波函数曲线，但是从波函数曲线看，当计算间隔减小时它的形状仍然随着计算点数的增加而变化，峰值逐渐减小.

波函数随着计算点数的变化而变化，这种不确定性可通过波函数的归一化解决，归一化系数可以利用数值积分求得.当然数值积分不可能像解析解一样积分区间取为(-∞，∞)，但因为在计算区间之外波函数全为零，所以积分区域可以选择为(x0，xM).经过归一化后的波函数相当于在解析解中确定了归一化常数，波函数应该是唯一的（当然仍可差一相位因子）.

图1中归一化后的波函数曲线是在区间[-5，]5内计算间隔分别取0.1、0.01和0.005时的波函数曲线，其本征值不变.图1中计算间隔取0.1、0.01和0.005时均使用细实线绘制，我们发现不同计算间隔的波函数曲线完全重合，并与解析解绘制的波函数完全一致.

计算间隔并不是固定的,它随着对本征的精度要求和具体的势函数不同而不同.正确的计算间隔应该是在本征精度要求范围内计算间隔变化不引起本征值变化为宜.

图1 计算间隔分别取0.1、0.01和0.005时分别用点划线、虚线和点线绘制未归一化的波函数曲线,用实线绘制的归一化波函数曲线，归一化波函数的曲线重合在一起.

3 计算区间的选择

由于在有限差分计算中，计算区间的端点假定ψ0=ψM=0，这相当于在计算区间的端点人为地加入一无穷高的势垒.只有当此无穷高的势垒不影响原来势中运动粒子的运动状态时才能得出正确的结论.如果位于端点处的无穷高势垒不影响粒子的运动状态，从物理上来讲应该是该粒子的运动区域应小于计算区间，就是说粒子不可能到达无穷高的势垒附近.这也就是说在计算区间的端点附近波函数应该已经为零而不是在端点处才等于零.从另一方面说，由于在计算区间外的波函数为零，所以波函数的导数亦为零，由波函数及波函数导数连续的条件，可知在计算区间的端点处的波函数导数亦应该是零，在真实的势中运动的粒子在任何地方导数都应该是连续的.与无限深势阱中运动的粒子不同，在无限深势阱中粒子可以运动到阱壁附近，所以在阱壁处波函数才降为零，当然此种情况下，波函数的导数并不连续.

图2、图3是对一维谐振子势利用有限差分法计算区间分别取[-2，2]、[-4，4]和[-6，6]得到的波函数曲线，其对应的本征值分别为λ=1.0739、λ=1.0000和λ=1.0000，则相应的能量本征值分别为0.5369ħω、0.5000ħω和0.5000ħω.由于在计算区间[-2，2]的端点谐振子的波函数并不为零，这说明在区间的端点人为地加上两无穷高的势垒对粒子的运动产生了影响，所以得出了错误的结果.当计算区间扩大为[-4，]4和[-6，6]，在接近计算区间的端点时波函数已经为零，因而位于端点的两无穷高的势垒并不影响问题的解，所以得出符合要求的本征值与波函数.

如果给出一个较为严谨的标准，应该要求在计算区间的端点波函数的导数为零.这样才能使有限计算区间端点波函数与计算区间外的波函数（波函数为零）光滑连接.实际情况也的确如此，图3分别给出了上述波函数对应的导数曲线，从图3看出当计算区间取为[-2，]2时,它的端点处波函数的导数并不为零（图3中的点划线表示），实际上从图2可以发现计算区间取为[-2，2]时端点的波函数曲线的斜率不为零（图2中的点划线表示），而从图2给出的区间取为[-4，4]、[-6，6]时波函数曲线（图中用实线和点线表示）在计算端点处均为零，从图3都能看出波函数导数曲线在计算区间的端点也均为零（图中用实线和点线表示）.

图2 计算区间取为[-2，2]、[-4，4]和[-6，6]时的波函数曲线分别用点划线、实线与点线绘制.

图3 计算区间取为[-2，2]、[-4，4]和[-6，6]时的波函数导数曲线分别用点划线、实线与点线绘制.

如果计算区间与计算间隔选取合适，那么当扩大计算区间时得到的本征值应该保持不变，并且计算区间扩大后的波函数与原来计算区间的波函数在相同区域内应该完全重合.这说明我们假定的边界条件ψ0=ψM=0（在端点的无穷高势垒处）并未影响原来粒子的运动，同时它们对应的波函数导数曲线也应该重合.如图2、图3所示.图2中计算区间分别取[-4，4]和[-6，6]绘制了两不同区间的波函数，其中区间[-4，4]和[-6，6]的波函数分别用实线与点线绘制，而图3给出了相应的波函数导数曲线.从图2和图3中可以看出在相同的区间[-4，4]内波函数和它们的导数是完全重合的.

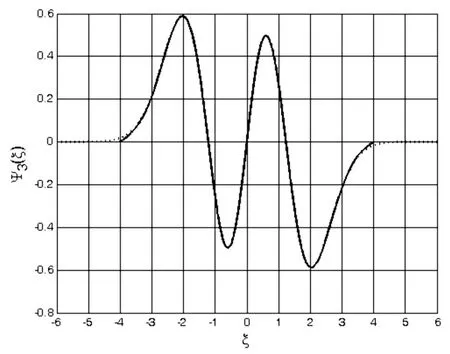
图4 计算区间取为[-4，4]和[-6，6]时,分别用实线和点线绘制的n=3的波函数曲线.

图5 计算区间取为[-4，4]和[-6，6]时,分别用实线和点线绘制的n=3的波函数的导数曲线.

另外，对于相同的势，随着粒子能量的提高，粒子活动的范围变大，计算区间将随之扩大，所以适合于低能级的计算区间，并不适合高能级的粒子.比如计算区间[-4，]4适合低能级的情况，但对于较高能级n=3时计算所得的能量本征值为E=3.5016ħω，其波函数曲线和波函数导数曲线如图4、图5所示，当计算区间取为[-4，4]时，波函数（图4中用实线表示）在两端点处等于零，但接近端点处的区域并不为零，而导数曲线在两端点并不等于零（图5中用实线表示）.从本征值和波函数及导数曲线来看，计算区间[-4，4]并不适合n=3的情况.但如果计算区间扩大为[-6，6]时，计算所得的本征值为E=3.5000ħω，而波函数与对应的波函数导数曲线如图4和图5中的实线所示.此时得到的能量本征值与波函数与解析解的是一致的.

4 非线性谐振子的势

下面我们用有限差分法讨论非线性谐振子的束缚态问题[3].假定非线性谐振子的势为：

为方便起见，引入无量纲的变量ξ代替x，它们的关系是如（6）式所示.令

非线性谐振子的哈密顿方程为可改写为

当β取0.1时，我们利用有限差分法求解本征值方程（14）式.计算时保持计算密度Δx=0.005不变,计算区间分别取[-5，5]和[-6，6]，得到的本征值均为0.4843，其波函数如图6所示，图中实线和点线分别表示计算区间取[-5，5]和[-6，6]时的波函数.虽然在变化计算区间时本征值并没有发生变化，但如果比较图6中的实线和点线可以看出在计算区间重合的区域内[-5，5]两者的波函数并不重合，并且波函数在计算区间左端点时，并不是在接近端点时已经为零，而是在端点处才突然降为零.将计算区间取为[-5，5]和[-6，6]的波函数的导数曲线绘制出来，如图7所示，发现它们的导数在左端点处均不为零，根据前面的讨论，我们判断在β取0.1时,并不存在束缚态.相同的讨论发现当β取1时，也不存在束缚态.

实际上对应于计算区间[-5，5]和[-6，6]的计算结果应该相当于在下述势中粒子运动的结果：

图6 计算区间取为[-5，5]和[-6，6]时的波函数曲线分别用实线与点线绘制.

图7 计算区间取为[-5，5]和[-6，6]时的波函数导数曲线分别用实线与点线绘制.插图为β=0.1时的势能曲线.

运动.在（16）和（17）所表示的势阱中运动，粒子的能级也为0.4843ħω.

图7绘制出β取0.1时的势能曲线.从图中可看出当β=1时，即Kmax=1.8519，文献[4]表1所说的对应于n=2的能级已经大于2ħω，即已经大于势左端的极大值Vmax=Kmaxħω=1.8519ħω，这种能量的粒子是不可能处于束缚态的.同理当β=1时，由于Vmax=Kmaxħω=0.0185ħω所以也不可能存在文献[4]表1中的束缚态能级.

实际上对于势为对称分布的情况，一般总存在至少一个束缚态，但如果势的分布并不对称，可能并不存在束缚态.根据有限差分法的计算和上述讨论，我们可以断定在β＞0.1时实际上并不存在束缚态能级.

当β取0.09时，即Vmax=Kmaxħω=2.2862ħω，计算区间取[-5，5]得到的第一个本征值E0=0.4877(ħω)，对应的波函数和波函数的导数如图8、图9中实线所示.计算区间取[-6，6]得到的本征值仍然是E0=0.4877(ħω)，对应的波函数和波函数的导数如图8、图9中点线所示.

图8 当β=0.09时，计算区间取为[-5，5]和[-6，6]时的波函数曲线分别用实线与点线绘制.

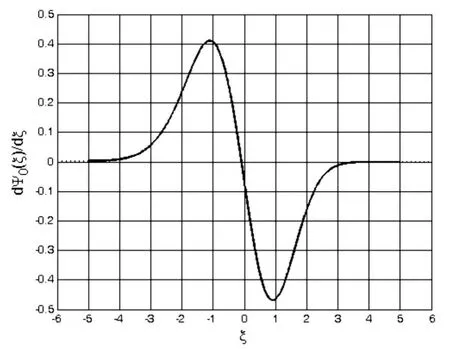
图9 当β=0.09时,计算区间取为[-5，5]和[-6，6]时的波函数对应的导数曲线分别用实线与点线绘制.

从图8和图9可以看出，两者在区间[-5，]5内是重合的,而两区间的波函数的导数在端点均为零.从此可以判断存在一个束缚态,不过通过计算可知此时并不存在更高级的束缚态.

4 总结

有限差分法求解定态薛定谔方程存在一系列的解,但这些解是否是满足给定势函数的束缚态解却需要进行考察.如果是束缚态的解，波函数应该在接近端点时已经为零，而不是在端点处突然降为零，这就要求在端点处波函数的导数应该为零.如果增大计算区间，得到的本征值应该基本不变，波函数在相同的计算区间内应该重合，如果在计算区间变化时波函数形态不同或者波函数的导数在区间端点不为零则有限差分法得到的解并不是原来给定势函数中运动粒子束缚态的解.

［1］刘建军，翟利学.有限差分法解能量本征方程［J］.北京工业大学学报，2008，34（3）：325～331.

［2］陈皓，高明，汪青杰.用有限差分法解薛定谔方程［J］.沈阳航空工业学院学报,2005,22（1）：87～88.

［3］白占国,刘 鹏,刘 平,等.用自洽平均值法计算非线性谐振子本征值［J］.大学物理，2008，27（9）：4～6.

［4］孙素涛,白志明.利用自洽平均值近似法巧解非线性谐振子问题［J］.大学物理,2010，29（6）：18～20.

［5］王小林.薛定谔方程的定态解与非定态解［J］.绵阳师范学院学报,2004（5）：47～48.