舰载光电伺服设备的系统辨识研究

周俊鹏，李 焱，王一卉，陈 娟

（长春工业大学 电气与电子工程学院，吉林 长春 130012）

1 引 言

可信度高的系统辩识获取电机机械时间常数Tm和固有放大倍数K的精度高，从而得到的电机传递函数模型准确。Tm的倒数是速度环的第二个拐点与调节器构成的系统影响BODE图低频段的走势，根据自控原理低频段增益及其走势直接影响系统稳态精度和动态精度，获得准确的Tm和K，能使控制模型准确，从而稳态、动态精度相对越高。常规系统辩识方法均从直流电机微分方程出发，并没有给出具体实施方案和实施过程［1－2］，只是利用电流与时间的关系图得到电流值的63.2%，其对应的时间即为机械时间常数而电机空载条件下运行，测出空载机械特性计算出电动机转动惯量，进而从导出公式中计算出Tm，但此方法只能适应具有大转动惯量的电机，没有太大的实用价值［3］。利用最小二乘构造俩参数线性方程，求出机械时间常数，其计算过程繁琐，只适用于某些电机而不具有普遍性［4］，构造更复杂的三参数最小二乘线性方程，仅仅从理论出发，没有实际工程背景，并不具有实用价值［5］。利用扫频法测出系统输入与输出的关系，在MATLAB中的simulink环境下开发递推最小二乘在线系统辩识，有其应用的局限性，精度不是很高［6］，卡尔曼滤波辩识算法，虽然给出来精度，但运算量过大，不利于舰载伺服系统对Tm的获取［7］。另外，有些方法导出Tm和时间的积分关系，将积分转化为梯形面积，但没有给出可信度、精度和工程可行性［8］。设计并利用Origin中近似逼近e指数函数拟合方法，其拟合误差小于0.1，可信度达到96%以上，解决了上述传统方法在获取电机机械时间常数精度低，可信度不高的问题。该项技术成功地应用在项目中，其拟合阶跃法对获取电机机械时间常数有很好的通用性和借鉴性。

2 伺服系统实现

2.1 PC104硬件平台

选X86架构的PC104嵌入式计算机作为目标机的伺服控制系统核心处理器，128M的CF卡作为外部程序机为核心处理器，128M的CF卡作为外部程序存储器。显控系统硬件实物如图1所示。分别设计定义了16C754四路串口的基地址分别为0x330、0x348、0x298、0x240，中断号分别为0x04、0x05、0x03、0x07。定义了82C55按照A路输入，B、C路输出的方式工作，基地址为0x3e0。FPGA为显控系统各芯片提供地址译码，并在外部准秒脉冲同步基础上产生16、25、400Hz的内部分频信号。通过INTEL 82559ER的网络控制芯片与外部通道台进行UDP网络的信息交互。

如图1所示，此硬件作为伺服系统辨识的平台，进行软件开发。

2.2 软件实现

由旋转变压器反馈出来的速度码值用aa＿0来表示，速度环开环输出码值用axk来表示。在TL16C754A口中断程序中设定axk的码值，编码器的采样周期0.0025s，这样就可以得到旋转变压器反馈速度值aa＿0。在程序的主函数中设置输出函数fprintf（fp1，"%04d%08.4lf%06ld／n"，＋＋Store＿Counter，aa＿0，encodera＿0），便于读出旋转变压器的值，流程图如图2所示。在CCS3.3中通过选择存盘操作可以得到DAT文件，即可直接用word的EXCEL文件打开，选择适当值。

人机交互界面采用多任务机制，具有优先级且任务间具备同步优点；多任务间的通信；中断延迟、任务切换、驱动程序延迟等操作系统行为是可知和可预测的。见人机交互界面图3，可以在界面上方便的显示、修改Tm和K值，不用编译函数体。

图2 A口中断流程图Fig.2 Flow chart of port A interruption

图3 人机交互界面图Fig.3 Man－machine interface diagram

此显控系统中右面前4列分别对应Tm、K、精度可信度，可见此人机交互界面直接读取Tm和K，及相关参数方面非常方便实用。

3 系统辨识的研究分析

3.1 近似逼近e指数函数理论依据

根据电压平衡方程式和负载为零时转矩平衡方程式，以及机电时间常数、电气时间常数计算公式可得：

其中：Tm为机电时间常数，Te为电气时间常数，Ω（t）为电机角速度，Ua为电机端电压。

其中：Ce为电动势常数，Φ为磁通量。

零初始条件下对式（1）做拉氏变换可得：

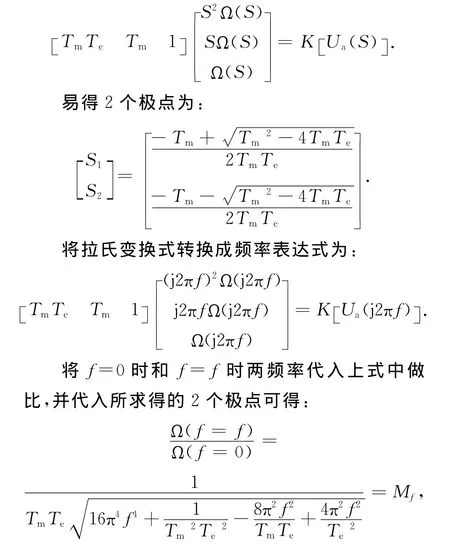
其中：Mf为电压频率为f时电机的角速度与电压频率为0时电机角速度的比值。由上式可得：

此公式作为阶跃法拟合曲线公式的依据。

3.2 近似逼近的e指数系统辨识模型

对于公式法带来的不便，且大多方法逼近真实值的精度很低，利用Origin拟合e指数函数方法其可信度高达96%以上，而且e指数的函数表达式用计算机很容易实现。在OriginPro7.0中根据公式：

将速度输出码值通过e指数函数转化成连续函数。根据式（2）使用拟合函数为：

其中：Y为旋转编码器反馈速度码值（即aa＿0的值），X为对应码值的序号。

P1、P2为最终需要拟合的未知量对应的机械时间常数和固有放大倍数。这样就可以通过测量得到的输出速度码值和对应的码值序号，通过式（3）以及 Origin拟合转换出未知量 P1、P2，得到最终的近似逼近e指数函数，从而获得高可信度和精度的系统辨识。

其中：P1，P2为通过Origin拟合出来的数值，axk为开环输出速度码值，T为采样周期800Hz。

4 Origin拟合实现及分析

4.1 系统辨识实现过程

为提高获得Tm和K的准确性，在试验中正向、反向各测两次，最后取平均值经过计算即可得到所需时间常数和放大倍数。在中断程序中设置速度开环输出的码值axk＝5000（正向），axk＝－5000（反向），用旋转变压器得到的2000多组值，导入originPro中，通过拟合可得所需近似逼近e指数函数，从而计算出Tm和K。

图4～图7中横轴为旋转变压器的码值所对应的序号值，纵轴为旋转变压器输出的码值，黑实线代表真实值曲线，红虚线代表按照近似逼近e指数函数300次连续逼近拟合后的曲线。从阶跃曲线中可以看出正向第一次拟合低码段，与真实曲线有细微的偏差。反向第一次测量其低码段有不明显的偏离，四幅拟合曲线图中的中高码段与真实曲线基本完全重合。可见应用Origin软件，按照近似逼近e指数函数去逼近真实曲线的效果很好。从图4和图6旁边的小放大图中可清楚看到。

图4 正向第一次拟合曲线图Fig.4 Positive first fitting curves picture

图5 正向第二次拟合曲线图Fig.5 Positive second fitting curves picture

图6 反向第一次拟合曲线图Fig.6 Negative frist fitting curves picture

图7 反向第二次拟合曲线图Fig.7 Negative second fitting curves picture

4.2 系统辨识精度分析

为方便得到试验结论，从Origin中提出数据得到表1，从表1中可清晰看出可信度都大于96%，误差均小于0.1，完全满足工程中所需精度要求。另外，可从表1中计算出P1的平均值为11067.22867，P1的误差平均值为0.0954。P2的 误差平均值为0.0257，P2的平均值为1530.074615。通过式（4）和式（5）最终得到电机固有放大倍数为：K＝2.2134，由于旋转变压器采样频率为800Hz即0.00125s可知电机机械时间常数为1.9126s。所求值亦可在前述显控系统中显示。

表1 试验数据拟合值表Tab.1 Test data fitted value

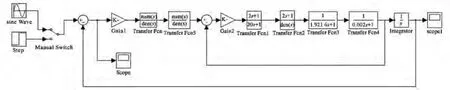
图8 光电经纬仪模型方框图Fig.8 Optical－electrionic theodolite model block diagram

4.3 控制精度对比分析

常规法计算机械时间常数公式为

其中：GD2为转动惯量，R为电阻，Ce为电动势常数，Cm为电磁转矩常数，Φ为磁通量。将厂家给出的电机常数带入式（6）中得Tm＝1.9987s。光电经纬仪要求最大角速度48°／s，最大角加速度22°／s2，经计算可得到等效正弦，将此参数带入图8的Sine Wave中。再分别将常规公式法得到的Tm＝1.9987和由e指数拟合阶跃法得到的Tm＝1.9216带入图8中的 Transfer Fcn4中，通过以上实际模型，经由 MATLAB中的SIMULINK仿真得到如图9（a）、（b）所示。

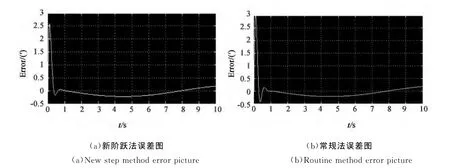
图9 跟踪误差对比图Fig.9 Tracking error comparsion picture

从图9中可清晰看到常规法最大误差3′，e指数阶跃法最大误差为2.5′，跟踪误差明显得到改善。

5 结 论

经过试验对比分析可知，用e指数拟合的阶跃法误差小于0.1，其置信度达到96%以上，弥补了公式法获取Tm上的种种不足，并且克服了其他方法获取Tm困难、可信度和精度不高的难题。从跟踪误差对比图中可看到新方法得到误差减小0.5’，可看到此方法在提高跟踪精度方面的优越性。同时方便的得到放大倍数K，电机电气时间常数Te可通过万用表测得，从而得到电机传递函数。在开发的人机交互界面上方便的修改、显示系统辩识结果。此方法在实际应用中方便、可行、有效，能够满足项目对Tm的精度需要。对系统辩识具有很好的通用性和借鉴性。

［1］苗本健.伺服电动机动态参数辨识问题［J］.伺服控制，2013（1）：39－41.Miao B J.Servo motor dynamic parameter identification problem ［J］.Servo Control，2013（1）：39－41.（in Chinese）

［2］蔡莎莎，毛晓明，陈志勇，等.同步电机调速系统参数辩识研究进展与展望［J］.广东电力，2012，25（10）：29－32.Cai S S，Mao X M，Chen Z Y，et al.Research progress and prospect of reference identification of synchronous motor speed control system ［J］.Guangdong Power，2012，25（10）：29－32.（in Chinese）

［3］张文海.伺服电动机的时间常数问题［J］.微特电机，2012，40（8）：75－76.Zhang W H.Time constant problem of servo motor［J］.Emotorcn，2012，40（8）：75－76.（in Chinese）

［4］冯清青.永磁直流电机测试系统研究［D］.哈尔滨：哈尔滨工程大学，2012.Feng Q Q.Research on permanent magnetic DC motor testing system ［D］.Harbin：Harbin Engineering University，2012.（in Chinese）

［5］刘琼.直流伺服系统模型及其辩识［J］.电气传动自动化，2012，34（6）：18－21.Liu Q.The model and identification of DC servo system ［J］.Electric Drive Automation，2012，34（6）：18－21.（in Chinese）

［6］张升.永磁无刷直流电机速度控制与模型参数辩识研究［D］.北京：北方工业大学，2013.Zhang S.Speed control and model parameters identification study of permanent magnet brushless DC motor［D］.Beijing：North China University of Technology，2013.（in Chinese）

［7］王建峰，张天宏.基于 MATLAB／XPC的直流电机参数辩识及双闭环控制研究［J］.测控技术，2011，30（12）：32－36.Wang J F，Zhang T H.Study on parameter identification of DC motor and double closed loop control based on MATLAB／XPC ［J］.Measurement ＆ Control Technology，2011，30（12）：32－36.（in Chinese）

［8］魏彤，郭蕊.自适应卡尔曼滤波在无刷直流电机系统辩识中的应用［J］.光学精密工程，2012，20（10）：2308－2314.Wei T，Guo R.Application of adaptive Calman filter in Brushless DC motor system identify－cation［J］.Optics and Precision Engineering，2012，20（10）：2308－2314.（in Chinese）

［9］喻冬梅，幸明强，汪建兵.无刷直流电动机Tm和Tl测量方法［J］.舰船科学技术，2011，33（10）：86－88.Yu T M，Xing M Q，Wang J B.Brushless DC motor Tmand Tlmeasurement method［J］.Ship Science and Technology，2011，33（10）：86－88.（in Chinese）

［10］潘先喜.永磁同步电机的伺服控制系统研究与实现［D］.武汉：武汉理工大学，2011.Pan X X.Research and implementation of control system of permanentmagnet synchronous motor servo［D］.Wuhan：Wuhan University of Technology，2011.（in Chinese）

［11］李焱，曹立华，王弟男.惯导平台下舰载光电搜索跟踪系统的控制［J］.光学精密工程，2011，19（5）：1126－1123.Li Y，Cao L H，Wang D N.Controlling of shipborne optoelectronic searching and tracking system based on inertial navigation platform ［J］.Optics and Precision Engineering，2011，19（5）：1126－1133.（in Chinese）

［12］李焱，陈涛，曹立华.舰载光电设备跟踪掠海目标的控制［J］.光学精密工程，2010，18（5）：936－941.Li Y，Chen T，Cao L H.Control of ship－based optoelectronic equipment for tracking near－sea targets［J］.Opticsand Precision Engineering，2010，18（5）：936－941.（in Chinese）

［13］赵磊，王学亮，巩岩.基于FPGA的液晶显示屏测试用标准白场装置［J］.液晶与显示，2014，29（1）：94－100.Zhao L，Wang X L，Gong Y.FPGA based white field apparatus for LCD calibration［J］.Chinese Journal of Liquid Crystals and Displays，2014，29（1）：94－100.（in Chinese）

［14］赵梓权，王瑞光，郑喜凤，等.LED显示屏的色域校正［J］.液晶与显示，2013，28（1）：92－98.Zhao Z Q，Wang R G，Zheng X F，et al.Color Gamut correction of LED Displays［J］.Chinese Journal of Liquid Crystals and Displays，2013，28（1）：92－98.（in Chinese）