从学生认知水平入手 用矛盾运动规律教学——《圆的周长》的教学设计与思考

游家水

（游家水：广州市越秀区署前路小学 广东广州510080 责任编辑：李士飞）

《圆的周长》是人教版义务教育课程六年级上册第四单元 《圆》第二节的内容。从单元编排上看，第四单元知识内容分为三部分：认识圆、圆周长、圆面积，本课时既是对圆认识的继续深化，又为圆面积的研究奠定基础。从“周长”知识体系编排上看，本课时是在三年级上册学习了周长的一般概念以及长方形、正方形周长计算的基础上做进一步研究。学生从学习直线图形到学习曲线图形，不论是内容还是研究问题的方法，都有所变化。教材通过对圆周长的研究，使学生初步认识研究曲线图形的基本方法，同时渗透“化曲为直”的转化思想和“类比猜想”的合情推理方法。

一、学生已有的知识经验

学生在三年级已经学习了周长的意义及测量周长的方法，有计算直线图形周长的知识基础，对曲线图形的周长也有较为深刻的认识，因此学生对于理解圆周长的意义、测量圆周长的方法都具有较丰富的认知经验。他们乐于接受化曲为直的数学思想，通过引导基本能够运用滚圆法、绕绳法等方法测量圆周长。

但六年级学生思维仍处于以具体形象思维为主的阶段，其抽象逻辑能力和合情推理能力还处于发展之中，学生往往缺乏思维的自觉性，缺乏主动调度相关旧知，自主迁移类推知识方法的能力。

对于推导圆周长计算公式而言，虽然学生认知结构中已有“封闭平面图形的周长可能与其图形内的某些线段具有倍数关系”的数学观念，“长方形、正方形的周长与其图形内的某些线段具有倍数关系”这一类比原型与方法例证，通过类比由加法交换律推导出乘法交换律、由加法结合律推导出乘法结合律的实践经验基础，以及学生画圆时所获得的旧知——“半径、直径决定圆的大小，半径、直径越长，圆的周长就越长，面积就越大”的知识经验，但就大多数学生而言，要求其借助类比猜想，在探索圆周长计算公式的过程中有意识地从“圆周长与什么有关”、“为什么要研究圆的周长与直径关系”、“周长与直径有什么关系”三个核心问题切入开展自主探究，进而理解圆周率的意义常常存在较大的困难。因此，教师在教学中要给学生提供必要的指导，以帮助学生进行探究。

二、运用矛盾运动规律学习新知

小学生学习数学的过程，其实质是一种矛盾运动，是学生发现矛盾、分析矛盾、解决矛盾的过程。学生学习新知识，当原有的知识、技能、方法不能解决面临的新数学现象、数学问题时，矛盾就出现了，从而产生认知冲突。这时，学生就会产生强烈的学习需要与求知欲望，从而充分调动相关旧知来解决问题。而当问题解决后，新问题会随之出现。瑞士著名心理学家皮亚杰就曾经指出：“任何认识，在解决了前面的问题后，又会提出新的问题。”

基于这一认识，本课采取了以下的教学策略：在“呈现矛盾—分析矛盾—解决矛盾”的过程中，激发学生的学习需要与求知欲。在“分析矛盾—解决矛盾”的过程中，渗透数学思想方法，培养学生初步逻辑思维能力和合情推理能力。把教学过程看作是“呈现矛盾—分析矛盾—解决矛盾”的过程。教学时注意创设问题情景，适时呈现矛盾，让学生在“冲突—平衡—再冲突—再平衡”的循环往复心理过程中，积极主动地参与知识的发生、形成与发展过程，提高分析问题和解决问题的能力，发展学生的空间观念，拓展学生的认知结构。

（一）创设情境，建立概念

创设问题情境，激发学生的求知欲望，并通过摸、指、描等体验活动，充分地建立圆周长概念。

首先，呈现问题情境：喜羊羊和灰太狼来到草地上跑步比赛，灰太狼是沿着正方形的花坛跑；喜羊羊沿着圆形的花坛跑。学生自然明确，灰太狼所跑的路程是正方形的周长，是我们已经学过的知识；喜羊羊所跑的路程是圆的周长，是我们本节课要研究的知识，揭示课题。其次，让学生感受新知识。让学生拿出圆形学具看一看、摸一摸、说一说、描一描圆周长，体会圆的周长的含义。

（二）实验探究，获取新知

新授环节以“呈现矛盾—分析矛盾—解决矛盾”为教学主线，在发现矛盾到解决矛盾的过程中，突出教学重点、突破教学难点。

1.测量实验，产生需要

在测量法的教学环节中，通过提供的典型材料，让学生体会到有的圆可以用“绕绳法”或“滚动法”等方法来测量出它的周长，渗透了“化曲为直”的数学思想方法。但同时也认识到“绕绳”、“滚动”等测量方法的局限性，引发其探索研究“计算公式”的必要性，使之带着问题学习新知识，探索解决问题的方法与途径，实现认知平衡。

2.再次实验，探究新知

圆周率是探究圆周长计算公式的中介点，它既反映了圆周长与直径的关系，同时利用圆周率，可以求出周长，因此理解圆周率的意义及其价值是推导计算公式的关键。在本环节，我设计了导向明确的问题，使学生再次经历呈现矛盾—分析矛盾—解决矛盾的过程，经历自主探究新知的学习过程。当学生在探索圆周长计算公式之时，直线图形周长的研究方法与曲线图形周长的研究方法不同，怎样寻找圆周长的计算公式？新的矛盾再次产生，这时可以适时地启发学生借助直线图形周长的规律：直线图形的周长与其图形内的某些线段存在倍数关系，由此类比：圆周长与直径是否也存在倍比关系？再次引发学生的认知冲突，指引探究的方向。

首先，我让学生想一想：圆周长与什么有关？引导学生回忆：画圆的时候，半径决定圆的大小，在同圆中直径是半径的2倍，所以圆的周长与圆的半径和直径都有关系，先研究周长和直径的关系。

第二步，我向学生抛出“圆的周长和直径有什么关系？”这一获取新知的核心矛盾，引导学生类比猜想：长方形的周长是它长加宽的和的2倍，正方形的周长是它边长的4倍，学生可能会猜想出圆的周长与直径之间可能也存在这样的倍数关系。那么圆的周长与直径的比值会不会是一个固定不变的数呢？板书：C÷d=□。

第三步是引导学生猜想，通过几何推理确定周长与直径关系比值的范围 （如下图）。

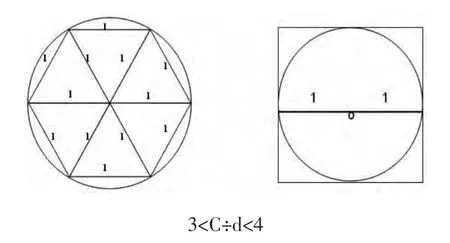
第四步是运用数据验证推理。学生四人小组分工合作，测量出圆周长，用计算器计算比值，并填写完成下表。

测量对象 圆的周长 圆的直径 周长与直径的比值圆1圆2圆3

学生实验后并汇报周长与直径的比值，发现：圆的周长是直径的3倍多一些。由于测量周长、直径时，总存在测量的误差，因此难以找到圆周长与直径的确切比值，怎样才能找到它们的比值呢？

第五步是介绍刘徽的“割圆术”，让学生体会随着圆内接多边形的边数增加，多边形周长近似于圆周长，渗透极限的数学思想；介绍祖冲之的圆周率，认识圆周率是一个无限不循环小数，用π来表示。并借数学文化激发学生的爱国情怀，培养民族自豪感。

第六步是推导出圆周长的计算公式：我们知道C÷d=π，所以可以推导出C=πd或C=2πr。

（三）多层练习，巩固新知

练习设计分为四个层次：第一层次是基本练习，安排运用公式计算圆的周长的题目，反馈学生对新知识的掌握情况。第二层次是安排两道看图求周长的题目，再次运用公式计算圆的周长，巩固新知，形成技能。第三层次是选择题，巩固圆周率的概念，知道π是一个无限不循环的小数；理解圆周率是一个定值，不受圆大小的影响；利用圆周率的近似值进行估算，体现解决问题的灵活性。第四层次是利用所学知识解决实际问题。包括：直接利用计算公式解决问题；利用计算公式解决变式练习；计算公式的逆向运用，培养学生逆向思维。

整个教学过程是以逻辑严密的数学问题为主线，以学生的学习认知基础为出发点，适时地创设问题情境，使学生经历多次“呈现矛盾—分析矛盾—解决矛盾”的过程，让学生在“冲突—平衡—再冲突—再平衡”的循环往复心理过程中，积极主动地参与知识的发生、形成与发展过程，提高分析问题和解决问题的能力，发展学生的空间观念，拓展学生的认知结构。