具有P-Laplacian算子的分数阶微分方程多点边值问题
宋利梅
(嘉应学院数学学院,广东梅州 514015)
0 引言
随着非线性科学的发展,人们发现用分数阶微分方程更能准确地描述一些自然现象的变化规律.因此,研究分数阶微分方程对解决非线性问题意义重大[1~2].而分数阶微分方程边值问题是分数阶微分方程理论的重要问题之一,近年来已经成为研究热点.相关的研究文献很多[3~8],文献[8]利用 Banach压缩映射原理研究了具有P-Laplacian算子的分数阶微分方程边值问题.

i=2,3,…,[α]-1,其中 φp是一个p-Laplacian 算子,φp(s)=|s|p-1s,p > 1.φq= φ-11,CDα表示α阶Caputo分数阶导数.1<α∈ℝ是一个常数.f∈C([0,1]× ℝ,ℝ )是非线性函数.受上述文献启发,本文研究具有P-Laplacian算子的分数阶微分方程多点边值问题,

解的存在性,其中1<α<2,CDα是α阶Caputo分数导数.ai>0,(i=1,2,…,m -2),0 < ξ1< ξ2< … <ξm-2<1,f∈C([0,1]×ℝ,ℝ )是非线性函数,φp是一个 P -Laplacian 算子.φp(s)=|s|p-1s,p>1,φq=由φp的表达式易得,φp为定义在ℝ上的严格单调递增的连续算子.
1 预备知识
定义1[3]连续函数u:(0,∞)→ℝ 的α >0阶Riemann-Liouville分数积定义为
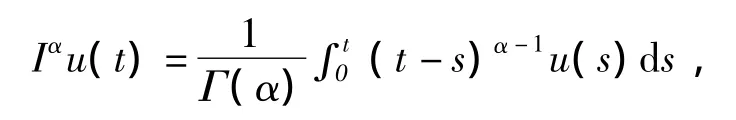
其中Γ(·)为Gamma函数.
定义2[3]连续函数u:(0,∞)→ℝ 的 α >0阶Caputo分数阶导数定义为
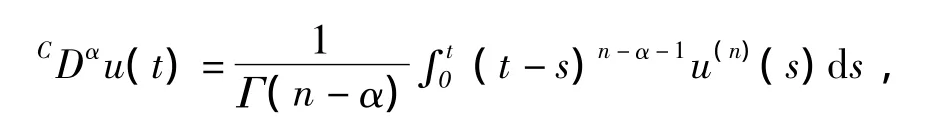
其中Γ(·)为Gamma函数.n为大于或等于α的最小整数.
注 1 IαIβf(t)=Iα+βf(t);DαIαf(t)=f(t).α >0,β >0,f∈L(0,1);B 是 Beta 函数,且 B(u,y)=
引理 1[3]假设 u∈Cn[0,1],那么
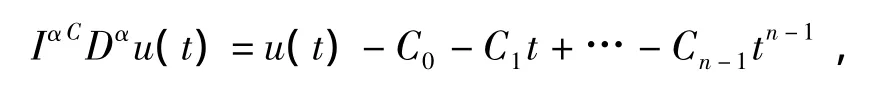
其中 Ci∈ℝ,i=1,2,…,n,n 是大于或等于 α 的最小整数.
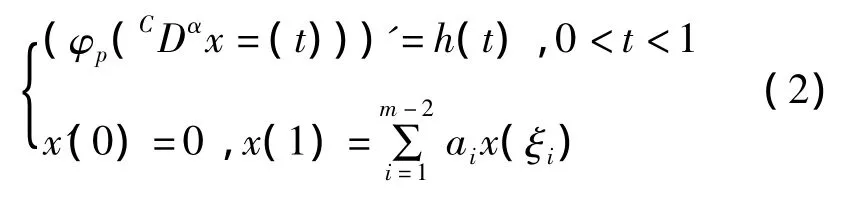
等价于积分方程

证明 由Caputo分数阶导数定义知CDαx(0)=0,对方程(φp(CDαx(t)))'=h(t)两边从 0 到 t积分,得 φp(CDαx(t))=h(s)ds,CDα(t)=φq(h(s)ds).根据引理 1,有 x(t)=Iα(φq(h(s)ds))+C0+C1t.由注 1,得
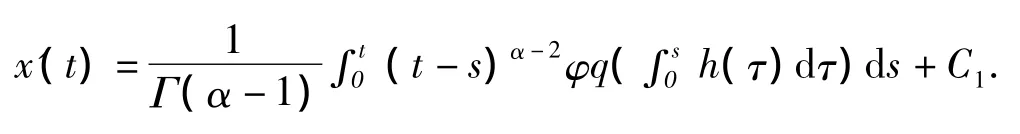
反过来,也很容易证明积分方程(3)的解是边值问题(2)的解.证毕.
本文主要结论的证明需要用到如下p-Laplacian算子的基本性质:
(1)若1<p<2,xy>0,且|x|,|y|>m >0,则

(2)若 p>2,|x|,|y|<M,则

2 主要结论
令 Banach空间 E=C[0,1],其范数为‖x‖:由引理 2 知,x∈E 是边值问题(1)的解当且仅当x∈E是下面积分方程的解.

定义算子 T0:E→E为 T0x(t)=φq(f(s,x(s))ds).再定义T1:E→E为

令T=T1◦T0,那么T:E→E是一个连续紧算子,事实上,由f的连续性知T也是连续的.Ω⊂E是一个有界子集.A>0是一个常数,使得对∀x∈Ω.有‖x‖ <A.令,则对
在当天吃完晚餐之后,我和家人一起来到可以直接看到101大楼的国父纪念馆,此时距离新年的到来还有4个小时,但人已经很多了,他们有的自带板凳,有的在草坪上铺上毯子,有的干脆席地而坐,抢占观看烟火的有利地形,摄影爱好者更是早早地布置妥当,力争拍出璀璨的烟火之美。
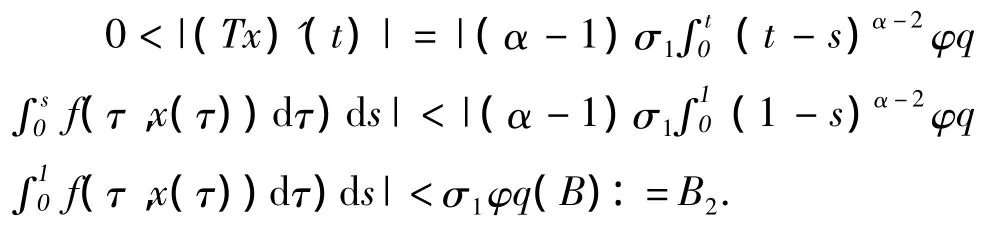
设x∈E,易知x是边值问题(1)的解当且仅当x是T的不动点.如果P>2,那么,有1 <q<2,有下面定理.
(H1)存在常数
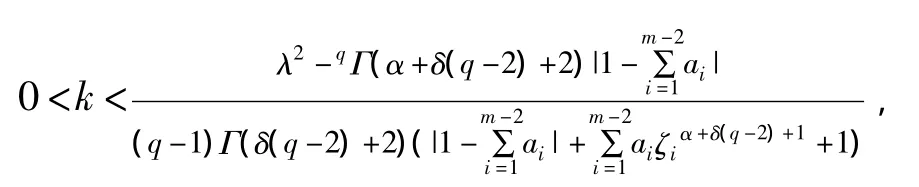
使得


证明 由式(6),有λtδ<f(s,x)ds.(t,x)∈[0,1]×ℝ .由式(4)及 T0的定义,对于任意的 x,y∈E有|T0x(0)-T0y(0)|=0.对 t>0,
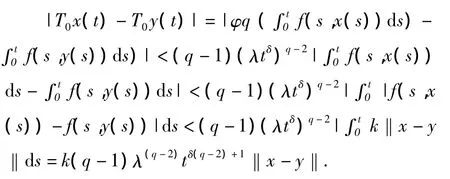
因此
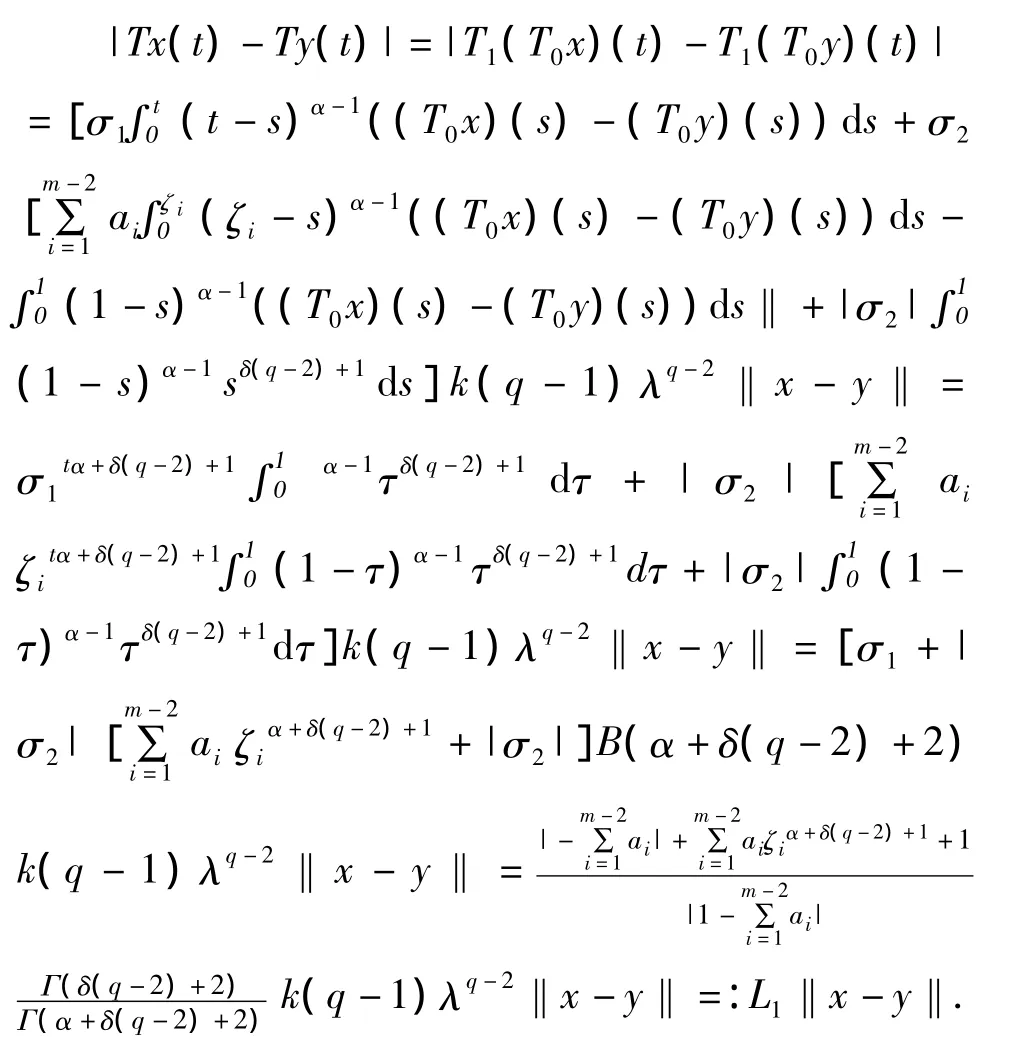
由条件(H1)知0<L<1.从而‖Tx-Ty‖ <L‖xy‖.这样,T:E→E是一个压缩映射.由Banach压缩映射原理,T在E中有唯一的不动点.即边值问题(1)有唯一的解.证毕.
(H2)存在常数λ>0,0使得 f(t,x)< - λδtδ-1,(t,x)∈[0,1]× ℝ,且|f(t,x)- f(t,y)|< k|x - y|,t∈[0,1],x,y∈ℝ .
该定理的证明与定理1的证明类似,略.
(H3)存在非负函数 g∈L[0,1],M:=g(t)dt>0和常数k,o<k<
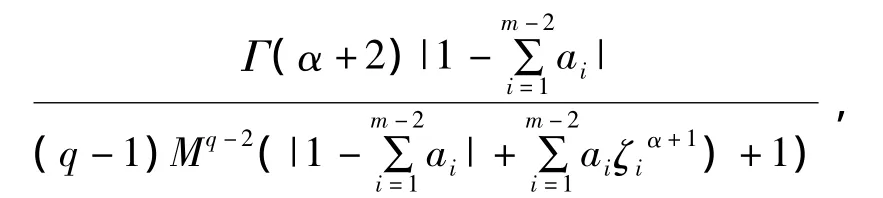
使得


证明 由式(8),对 t∈[0,1],有
|f(s,x(s))ds|<|f(s,x(s))|ds<q(s)ds=M.由(5)和(9),对任意的 x,y∈E,有

因此
|Tx(t)-Ty(t)|=|T1(T0x)(t)-T1(T0y)(t)|τ d τ]k(q-1)Mq-2‖x-y‖ <=:L1‖ x - y‖, 其 中 L1=‖x - y‖=:L1‖x-y‖.由条件(H3)知0 <L1<1,从而‖Tx-Ty‖<L1‖x-y‖.这样,T:E→E是一个压缩映射.由Banach压缩映射原理.T在E中有唯一的不动点.即边值问题(1)有唯一的解.证毕.
作为应用,现举例如下.
例1 考察边值问题


由定理1知,边值问题(10)有唯一解.
例2 考察边值问题.
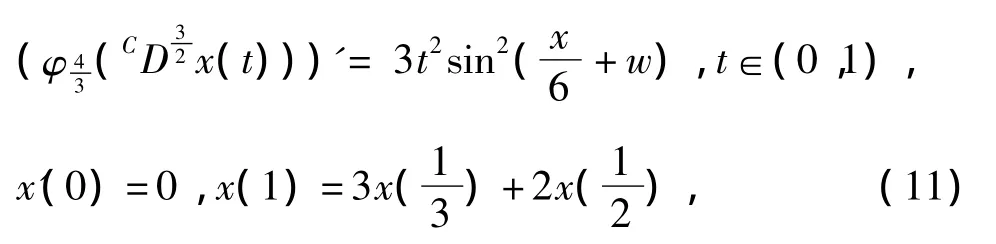
[1]KILBAS A A.SRIVSTAVA H M.TRUJILLO J J.Theorv and Applications of Fractional Differential Equaitions[M].North - Holland Mathematics Studies.Elsevier Science.2006.
[2]PODLUBNY I.Fractional Differential Equantions[M].San Diego.Academic Press.Calif USA.1999.
[3]白占兵.分数阶微分方程边值问题理论及应用[M].北京:中国科学技术出版社,2012.
[4]BAI Z B.LV H S.Positive solutions for boundarv value problem of nonlinear fractional differential eauation[J].J Math Anal Appl..2005,311(2):1202 -1208.
[5]ZHANG S Q.Exostence of a silution for the fracitional differential equantion with nonlinear boundarv conditions[J].Computers and Mathematics with Applications.2011,61(4):1202-1208.
[6]SONG L M.WENG P X.Existence of positive solutions to boundarv value problem for a nonlinear fractional differential equation[J].Chin.Quart.J.of Math.2012,27(2):293-300.
[7]CHEN T Y.LIU W B.An anti- periodic boundarv value problem for the fractional differential eauation with a p-Laplacian oquacian operator[J].Applied Mathemayics Letters.2012,25(11):1671 -1675.
[8]LIU X P.JIA M.XIANG X F.On the solcabilitv of a fractional differential equation model involving the p-Laplacian operator[J].Computer and Mathematics with Applications .2012,64(10):3267 -3275.

