考虑斜拉索松弛的盘绕式伸展臂振动模型

韩建斌 黄 海 马海波

(北京航空航天大学 宇航学院，北京100191)

盘绕式伸展臂是一种空间伸展臂，广泛用于太阳电池阵、探测臂等空间伸展机构.伸展臂完全展开后形成三角形截面桁架结构，依靠横杆、纵杆、斜拉索的相互作用保持稳定.但其结构特点又与普通桁架不同:

1) 横杆处于弯曲状态[1－2]，此时虽然承受一定压力，但拉压刚度很小[3];

2)斜拉索处于拉紧状态，不能承受压力，在变形较大时会发生松弛现象[4－6].

进入应用以来，针对伸展臂展开状态下的变形及振动特性研究[3，7－9]一直是盘绕式伸展臂研究工作的重要内容.但由于斜拉索的松弛造成刚度的改变[10]，使得考虑斜拉索松弛的伸展臂振动研究有一定难度.理论上针对刚度随变形阶跃变化的分段线性刚度系统，在单自由度或多自由度下已有较为合适的方法可以借鉴[11－14]，但应用在连续系统下还需要一定的变换.

本文以北航微小卫星用盘绕式伸展臂为对象，在Ansys环境下建立了有限元模型，分别计算了斜拉索松弛前后两种结构下的伸展臂基频.为研究振幅较大而使结构不断变换时盘绕式伸展臂的基频特性，建立满足分段线性刚度特性的等效连续梁模型.使用等价线性化方法，并代入斜拉索松弛判据及松弛前后两种结构下的基频，得到伸展臂等效振动频率随端部振幅的变化关系.最后利用Ansys的瞬态分析对上述等效频率结果进行了仿真验证.该模型探讨了一种考虑斜拉索松弛时盘绕式伸展臂振动的初步的研究方法，研究了斜拉索松弛对伸展臂振动系统的影响，可以作为对盘绕式伸展臂进行振动控制的理论基础.

1 盘绕式伸展臂有限元建模介绍

本文以图1所示盘绕式伸展臂为研究对象.

图1 盘绕式伸展臂

盘绕式伸展臂包括纵杆、斜拉索、横框等部件.横框由铰链、横杆组成三角形框架，其中横杆与铰链之间为铰接状态，在研究横杆变形时按照两端简支处理.

模型结构示意图如图2所示，由横杆、纵杆、斜拉索及铰链等部分组成.3根纵杆在铰链位置可以绕OA，OB，OC旋转，横杆与铰链之间为铰接状态.以铰链B为例，AB，BC杆对应的铰接轴为BD，BE.

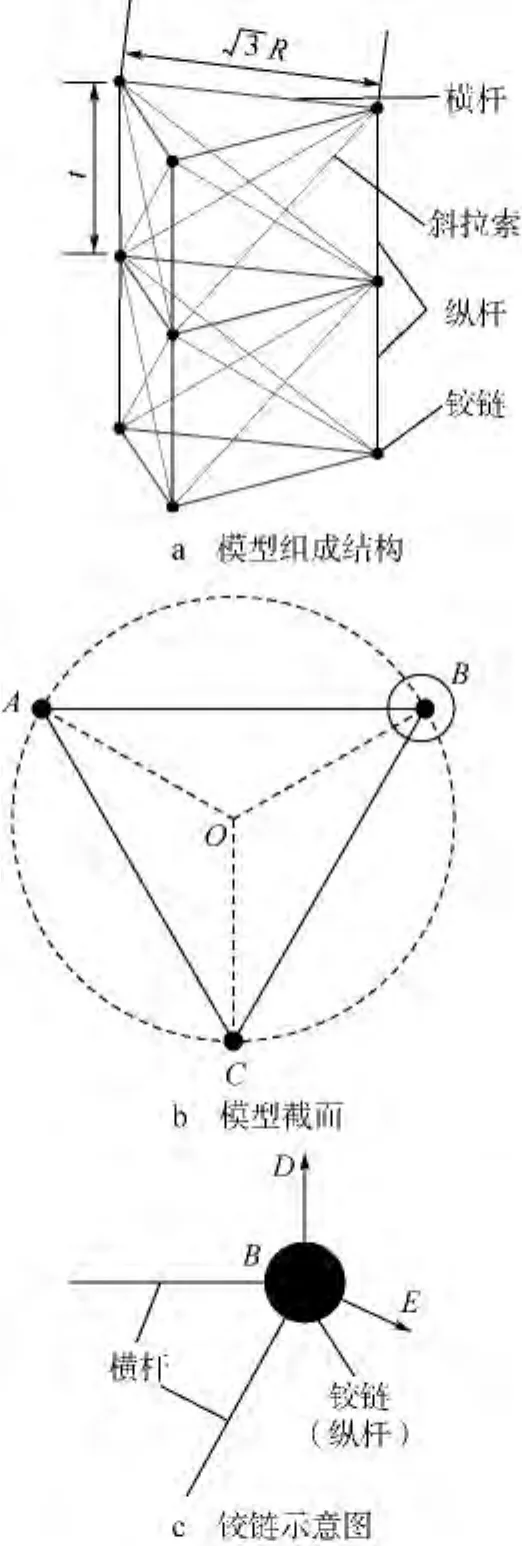
图2 模型结构示意图

盘绕式伸展臂和普通桁架不同，其横杆处于弯曲状态，斜拉索受拉张紧但不承受压力.针对这两点的处理方法如下.

1.1 弯曲横杆及预紧力建模方法

盘绕式伸展臂在展开后及振动过程中，由于预紧力的作用，横杆始终保持弯曲状态，如图3a所示.此时横杆处于材料力学中的压杆屈服状态，两端连线方向等效拉压刚度较小，因此相关文献中按照恒力建立横杆模型[8].图3b所示为两端简支压杆受压屈服前后的受力与变形关系.伸展臂展开后，横杆处于图3b的虚线框所示受力状态[3].

图3b的横轴为横杆两端距离减小量与原长的比值.文献[15]利用弹性细杆的Kirchhoff动力学给出了两端简支压杆弯曲后压力与变形的公式，可以准确描述图3b虚线框内的曲线:

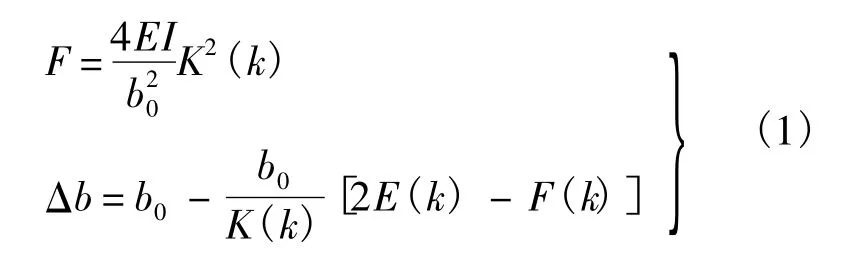
式中，EI为压杆弯曲刚度;b0为直线状态压杆全长;k为随压杆弯曲程度增大而变大的量;K(k)，E(k)，F(k)为关于 k的椭圆积分[15].

根据式(1)，在保证横杆长度、截面积不变的情况下，可以计算出一个满足图3b虚线框曲线内受力与变形关系的等效弹性模量Eeq.将Eeq作为横杆材料的弹性模量.

图3 横杆弯曲状态及弯曲前后张力变化曲线

在多数有限元软件中预紧力可以用设置初始应变的方法很方便地加载[9]，因此本文通过为横杆设置初始应变加载预紧力.

弯曲横杆的作用在于利用其承载能力对变形的不敏感，来保证预紧力大小的一致[1].考虑实际上预紧完成后横杆弯曲程度并不是很大，因此横杆此时所受压力和横杆作为压杆的欧拉失稳载荷Fcr相近，即在盘绕半径、节距、横杆刚度及横杆的连接方式确定的情况下，预紧力是确定的.因此横杆的初始应变设置为

设置横杆的预应变为－εini，相当于横杆发生－εini大小的应变后长度为b.此时横杆对两端有Fcr大小的张力，如图4a所示.因此设置－εini之后相当于给伸展臂施加了图4b所示的静力载荷.

用静力分析可以得到含预应力的盘绕式伸展臂模型.

1.2 斜拉索松弛处理

在变形较大时，单侧斜拉索会发生松弛现象.Ansys的Link10单元可以设置为单向受拉杆单元，但在模态分析中不考虑非线性特性，Link10仍然作为普通可拉压杆件处理.针对斜拉索松弛后的盘绕式伸展臂结构进行如下分析.

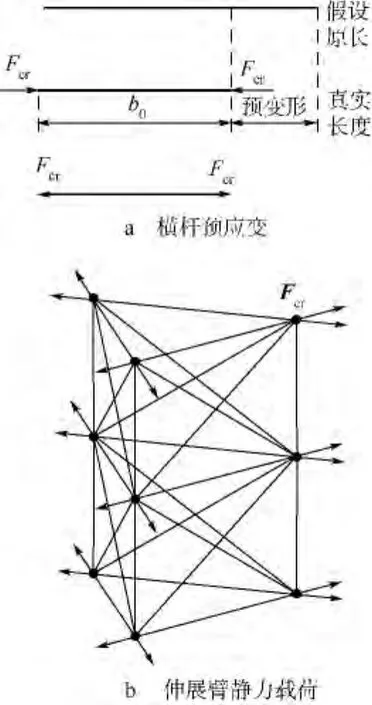
图4 横杆预应力示意图

通常斜拉索拉压刚度较大，因此当桁架横向有很小变形时，斜拉索即开始松弛.此时分析其受力情况可忽略桁架整体的横向变形影响.以带斜拉索的二维桁架为对象进行分析，当顶端受横向力F作用使得斜拉索松弛时，将松弛拉索去除，将拉紧索按杆件建模.如图5所示(实线F).

图5 二维桁架变形分析

图5a中斜线为不受压的绳索，图5b斜线为单根可拉压杆.设节距为t，斜杆长为l，CD长为b.图5 中:

通常桁架两端均连接刚性部件，因此忽略AB，CD两根杆件的变形.由单位载荷法可以计算图5a和图5b的端部横向位移，二者均为

同理可以证明，当横向力反向时(图5虚线F)，图5a和图5b的端部横向位移仍为式(4).

由此可以说明单根斜杆与2根交替张紧的斜拉索作用相同，两种结构的整体横向刚度相同.因此对2根斜拉索交替松弛的结构进行模态分析时，为了不在结构中加入斜拉索这种非线性单元，用1根可拉压杆代替2根斜拉索进行建模.

1.3 盘绕式伸展臂有限元模型

针对北航微小卫星用盘压杆建立有限元模型.用上述方法处理弯曲横杆、斜拉索等盘绕式伸展臂的特殊元素，在Ansys环境下建立有限元模型.横杆选用Link8单元，斜拉索用Link10单元.其中Link8为Ansys中三维轴向拉伸-压缩杆单元，具有两个节点，不考虑弯曲及扭转.Link10和Link8相似，但可以设置为单向受压或受拉(可用于静力及瞬态分析)，因而很适合用于斜拉索建模.在下文模态分析部分，Link10单元按普通可拉压杆件处理，在静力及瞬态分析部分可以设置为单向受拉单元.

通过给Link8单元设置－εini大小的初始应变来设置预紧力.纵杆选用普通梁单元Beam188，且每节纵杆分3段建立.铰链按点质量建模[8]，使用Mass21建立.

此外一般伸展臂端部会连接一定的刚性部件，因此将最终模型一端的3个铰链固定，自由端3根横杆按普通杆件建模，E=3.387×104MPa，且无初始应变.

各单元详细参数见表1.

表1 模型详细参数

图6 斜拉索松弛前伸展臂有限元模型

计算斜拉索松弛后盘绕式伸展臂的结构频率时，用Link10单元建立单根杆单元，代替2根交替松弛的斜拉索建模，见图7.

图7 斜拉索松弛后伸展臂有限元模型

1.4 模态计算

对上述盘绕式伸展臂模型进行模态分析.计算预紧状态下伸展臂的模态需要考虑预应力.在Ansys中先后进行静力和模态分析，并在二者的设置中打开预应力效应选项(PSTRES ON)，即可得到预紧状态下伸展臂的模态结果.用图6、图7所示模型分别进行上述计算，得到模型第1阶振动模态如图8所示.

图8 盘绕式伸展臂模态分析结果

图8a所示斜拉索松弛前伸展臂基频为f1=49.15 Hz.图8b所示单侧斜拉索松弛状态的伸展臂基频为f2=0.452 Hz.二者相差很大，这是因为盘绕式伸展臂的横杆处于压杆屈服状态，使其等效拉压刚度很小(见1.1节弯曲横杆建模)，使得斜拉索松弛后的横向刚度极小[9].以斜拉索松弛前后这两种结构的频率为条件，计算振幅较大时盘绕式伸展臂结构不断变换的等效频率.

2 盘绕式伸展臂非线性振动分析

由上述分析可知斜拉索松弛前后的两种结构的基频不同.当振幅较大时，盘绕式伸展臂必然在两种结构间不断变换.下文首先研究斜拉索松弛时伸展臂的变形大小，在此基础上建立考虑斜拉索松弛的盘绕式伸展臂振动模型.此外当振型为第2阶以上时，各层斜拉索松弛情况较为复杂.且系统的振动能量主要体现在第1阶振型.因此如未特别说明，下文只考虑伸展臂第1阶振型.

2.1 斜拉索松弛时的盘绕式伸展臂变形

利用上文建立的斜拉索松弛前的伸展臂模型(图6)进行仿真计算，得出斜拉索松弛判据.

固定底端，在另一端铰链A上加载横向力F.在长度方向上均匀选择3根发生松弛的斜拉索a，b，c，研究其受力变化，如图9 所示.

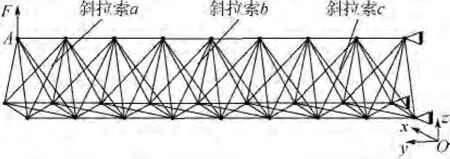
图9 盘绕式伸展臂横向变形计算模型

以A点横向位移为横轴，斜拉索拉力为纵轴画出曲线如图10所示.

由于伸展臂是从预紧状态发生变形的，图10中3根斜拉索拉力初始值都不是0.3条曲线几乎完全重合，在端部位移达到δ时同时变为0，表示3根斜拉索同时发生松弛.图10曲线是根据表1数据建立模型得到的结果，δ≈0.64 mm.

在只考虑第1阶振型的情况下，将δ作为斜拉索是否松弛的判断标准:端部位移大于δ时，斜拉索发生松弛.此外由于盘绕式伸展臂的横向刚度与变形方向无关[5，16]，因此变形方向改变时斜拉索松弛判据不变.

2.2 振幅较大时盘绕式伸展臂的等效频率

当端部位移大于δ时，伸展臂刚度发生变化，这是一个典型的分段线性刚度系统[11，17].在长细比较大时，盘绕式伸展臂的整体振型同连续梁结构相同.在保证整体振型及边界条件一致的条件下，将伸展臂等效为一段悬臂梁结构.斜拉索松弛前后的两种结构的振动方程如下所示:

式(5)、式(6)分别与图6、图7两种结构对应，对应的第1阶频率分别为fa1，fb1;(EJ)1，(EJ)2分别为斜拉索松弛前后的等效刚度;为盘绕式伸展臂平均线密度.

伸展臂在发生一定变形后刚度变为(EJ)2.其惯性力变化示意图如图11所示.

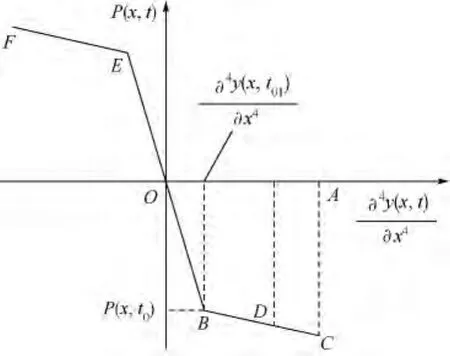
图11 分段惯性力

伸展臂在E，B间振动，惯性力可以表示为

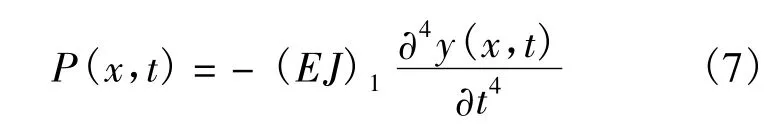
以D点为例计算BC段惯性力.在B点基础上考虑(EJ)2的作用，即

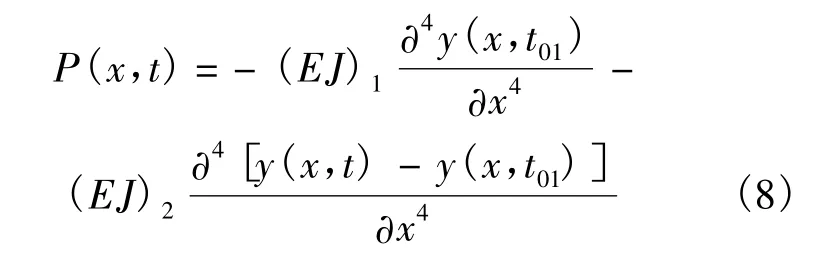
设伸展臂在O→C振动过程中在t02时刻斜拉索松弛.E→F→E过程惯性力可以表示为

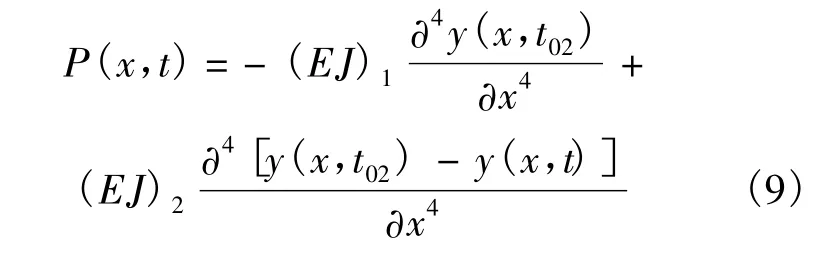
E，B点伸展臂变形关于平衡位置对称，有

因此式(9)可以转化为

B→C→B过程有 y(L，t) ＞δ，E→F→E 过程有 y(L，t) ＜ － δ.可以用 y(L，t)代替 t01，t02表示斜拉索是否松弛.得斜拉索松弛后的振动方程:

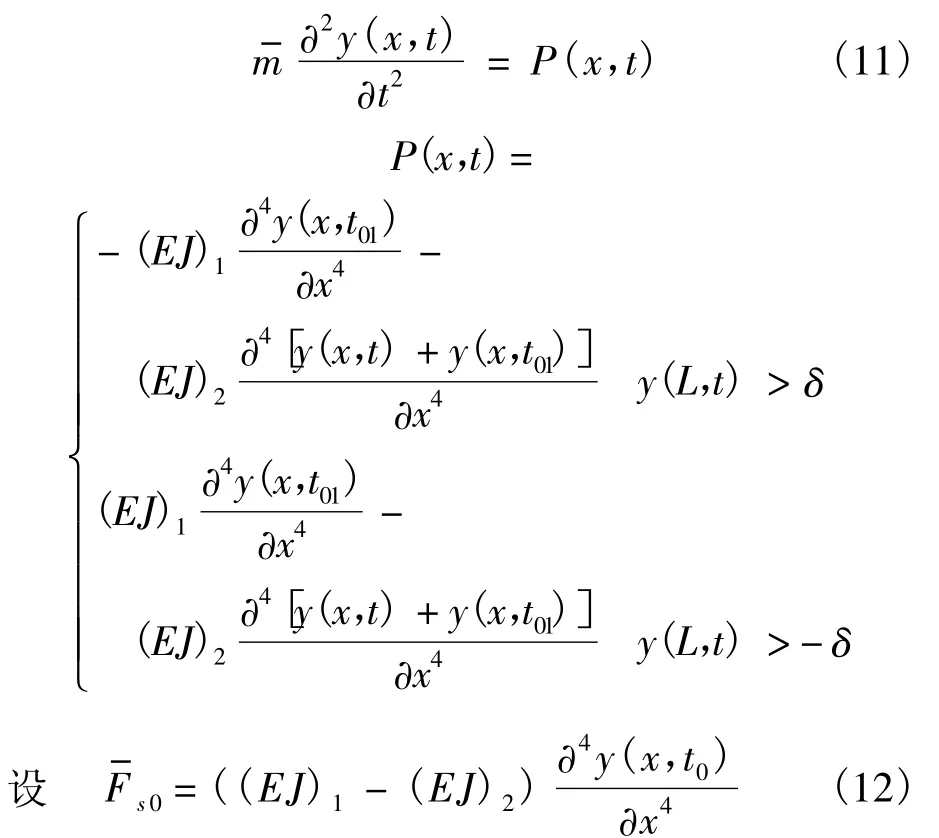
结合式(7)、式(11)、式(12)，在只考虑盘绕式伸展臂以式(5)的第1阶振型振动时，振动方程可以表示为

式中Y1(x)为式(5)的第1阶振型函数，将式(14)代入式(13)可以得到

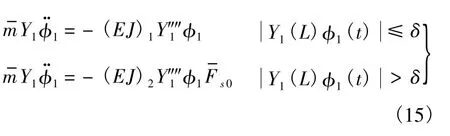
将式(15)两端同乘以Y1(x)，沿x方向积分得到

式中

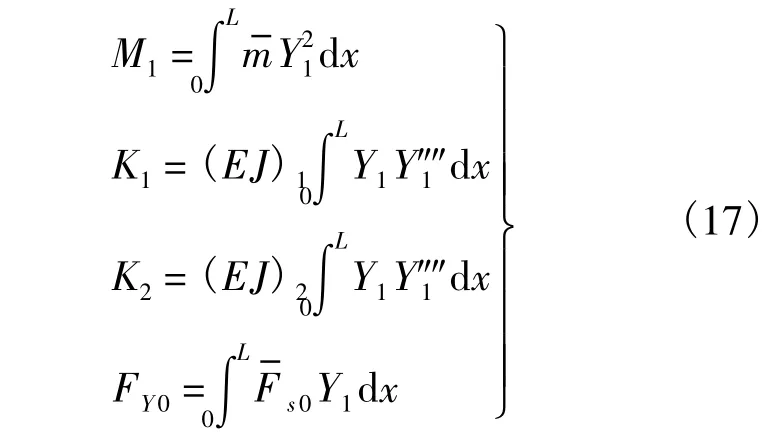
由于Y1(x)是式(5)的振型函数，因此式(5)表示的悬臂梁基频:

同时对于悬臂梁来说，Y1(x)只与边界条件有关，因此同样是式(6)的振型函数[18].对应悬臂梁基频:

根据文献[14]的等价线性化法，设非线性方程(16)的近似解为

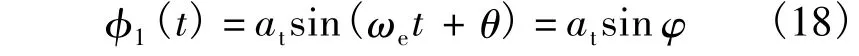
P1(t)可改写为以下形式:

式中φe为与斜拉索松弛瞬间等效梁端部振幅对应的相位角.

端部位移为

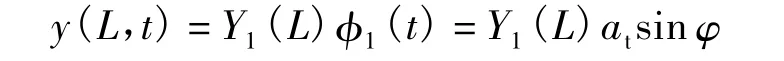
事实上Y1(L)at就是端部振幅A.则相位角φe为

系统的等价刚度可以由下式求得[14]:

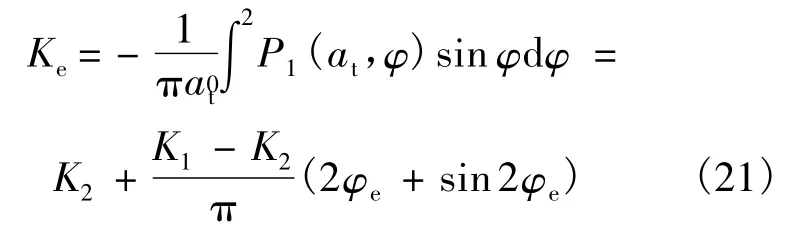
从而得到系统的等效频率:

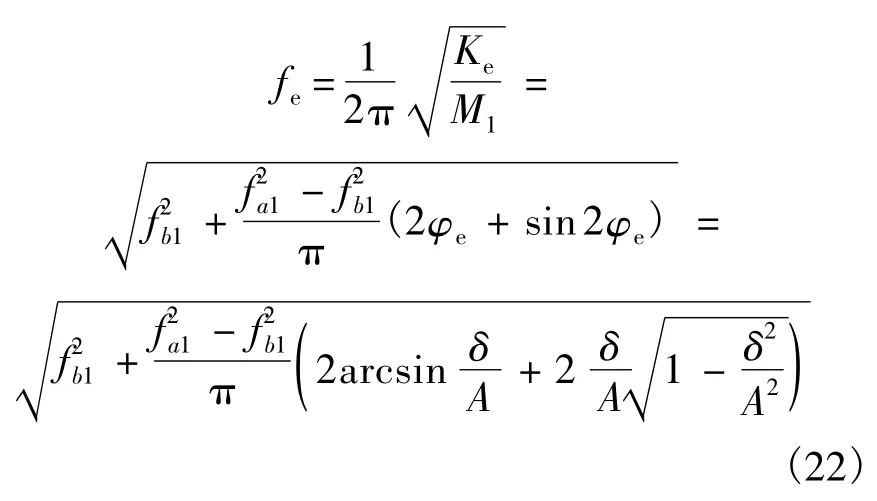
式(22)表明在如式(16)所示的分段刚度非线性系统内，等效频率和线性系统的频率概念有所不同.不再是系统的固有特性和系统变形大小有关.

3 Ansys瞬态分析

用上文建立的斜拉索松弛前的盘绕式伸展臂Ansys模型(见图6)进行时域分析，对上述结果进行验证.斜拉索使用的Link10单元在瞬态分析中可以体现只受拉的特性.如图9所示在A点加载横向力F.作用0.02s后去除F，计算伸展臂之后的运动.以A点位移表示伸展臂振动，如图12所示.

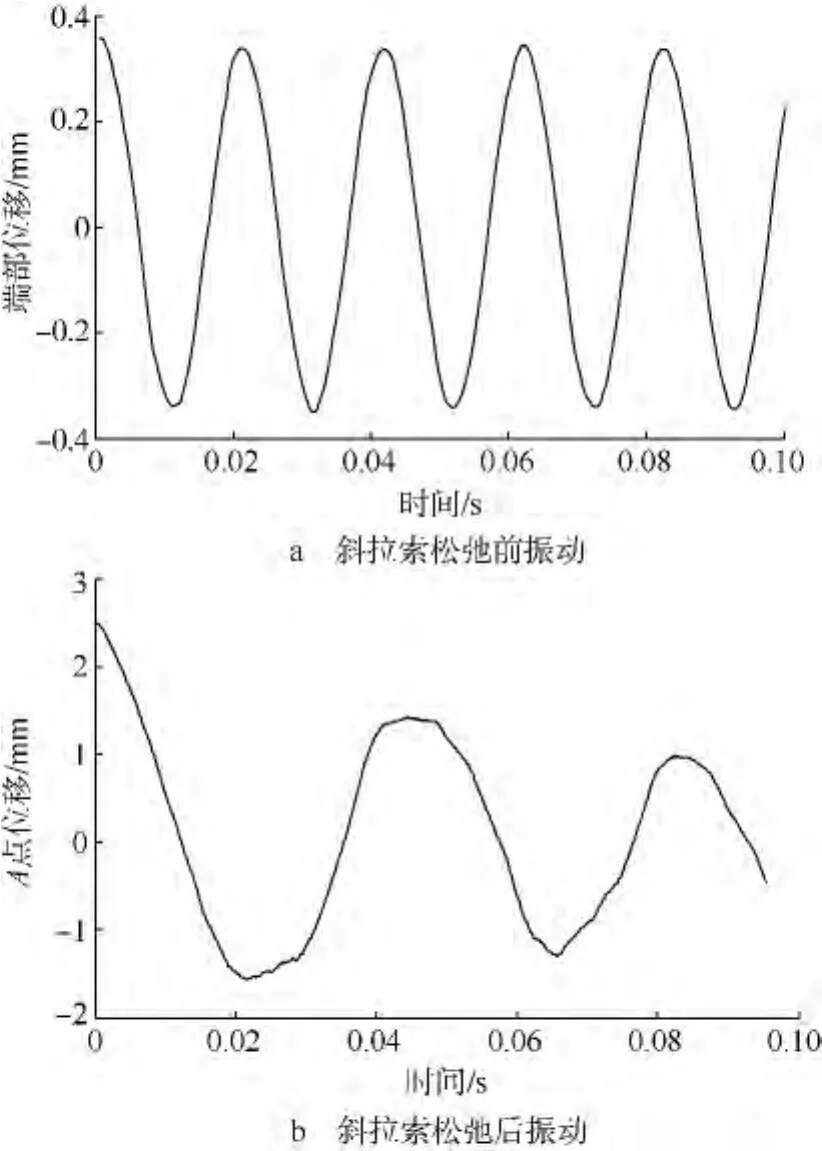
图12 Ansys瞬态分析结果

图12a中伸展臂端部振幅为0.34 mm，小于斜拉索松弛判据(δ≈0.64 mm).此时斜拉索没有松弛，振动频率约为48.59 Hz.

图12b伸展臂端部振幅大于δ，斜拉索已经松弛，振动频率约为29.58 Hz.

从图12可以看出，二者振动频率相差很大.改变F大小，可以得到与不同振幅对应的振动曲线，从而得到与振幅对应的频率.仿真频率结果及按式(22)计算得到的频率结果如表2所示.

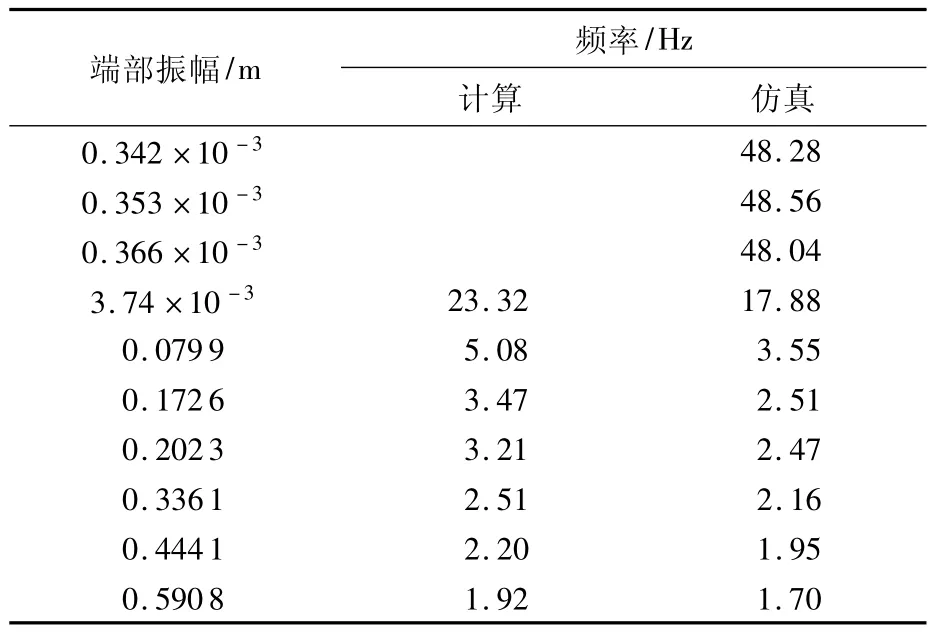
表2 盘绕式伸展臂频率变化

将表2数据画成曲线如图13所示.

图13 盘绕式伸展臂振动频率随端部振幅的变化

可见瞬态分析结果与上文推导的等效频率基本吻合，频率随端部振幅增大而呈指数趋势减小，并逐渐趋近于斜拉索松弛后的频率fb1.

4 结论

盘绕式伸展臂完全展开后形成稳定的三角形桁架结构，但其特有的弯曲横杆、可松弛斜拉索的特点使得振幅较大时伸展臂频率发生改变.振幅越大频率越小，并且趋向于一个斜拉索松弛后的频率.本文建立的盘绕式伸展臂振动模型指出了斜拉索松弛对伸展臂振动性能的影响，并且验证了一种考虑斜拉索松弛时盘绕式伸展臂振动特性的研究方法.该模型可用于评估外部干扰力对盘绕式伸展臂性能的影响，同时在确定工作环境的外部干扰力条件下，可应用该模型给出盘绕式伸展臂的刚度设计要求.

References)

[1]Murphy D，Trautt T，McEachen M，et al.Progress and plans for system demonstration of a scalable square solar sail[C]//Advances in the Astronautical Sciences.Maui，Havaii:Univelt Inc，2005，119(1):51 －68

[2]Murphy D M，Macy B D，Caspar J L.Demonstration of a 10-m solar sail system[C]//45th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆ Materials Conference.Palm Springs，California:AIAA，2004:698 －708

[3]Murphy D M，Murphey T W.Scalable solar-sail subsystem design concept[J].Journal of Spacecraft and Rockets，2003，40(4):539－547

[4]Greschik G.Truss beam with tendon diagonals-mechanics and designs[J].AIAA Journal，2008，46(3):557 － 567

[5]Murphey T W.Symbolic equations for the stiffness and strength of straight longeron trusses[C]//47th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics＆ Materials Conference.Reston，VA:AIAA，2006:6298 －6311

[6]郭宏伟，刘荣强，邓宗全.柔性索对空间索杆铰接式伸展臂性能影响分析[J].哈尔滨工业大学学报，2010，42(1):55－59

Guo Hongwei，Liu Rongqiang，Deng Zongquan.Influence of flexible cable on performance of space cable-strut deployable articulated mast[J].Journal of Harbin Institute of Technology，2010，42(1):55－59(in Chinese)

[7]Chen T，Wang J T.Modeling of triangular lattice space structures with curved battens[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics ＆ Materials Conference.Austin，Texas:AIAA，2005:2096 －2109

[8]McEachen M E，Trautt T A.Confirmation of new analytics for ultra-light lattice column strength using a 40-m flight article[C]//50th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics＆ Materials Conference.Reston，VA:AIAA，2009:2169-1－18

[9]Wang J，Li D X，Jiang J P.Finite element modeling and modal analysis of coilable mast[J].Applied Mechanics and Materials，2012，226-228:299 －302

[10]Jones T C，Smith H B，Mikulas M，et al.Finite element modeling and analysis of large pretensioned space structures[J].Journal of Spacecraft and Rockets，2007，44(1):183 －193

[11]Jiang D，Pierre C，Shaw S W.Large-amplitude non-linear normal modes of piecewise linear system[J].Journal of Sound and Vibration，2004，272(3):869 －891

[12]闫政涛，翁雪涛，朱石坚，等.刚度分段线性系统的自由振动解析研究[J].噪声与振动控制，2010，30(6):18 －22

Yan Zhengtao，Weng Xuetao，Zhu Shijian，et al.Analytical solution of free vibration of systems with piecewise linear stiffness[J].Noise and Vibration Control，2010，30(6):18 － 22(in Chinese)

[13]吕娜玺.两自由度分段线性系统模态分析[D].兰州:兰州交通大学，2012

Lü Naxi.Normal modal analysis for a two degrees-of-freedom piecewise linear systems[D].Lanzhou:Lanzhou Jiaotong University，2012(in Chinese)

[14]闻邦椿，李以农，徐培民.工程非线性振动[M].北京:科学出版社，2007:32－37

Wen Bangchun，Li Yinong，Xue Peimin.Engineering nonlinear vibration[M].Beijing:Science Press，2007:32 －37(in Chinese)

[15]刘延柱.弹性细杆的非线性力学:DNA力学模型的理论基础[M].北京:清华大学出版社，2006

Liu Yanzhu.Nonlinear mechanics of thin elastic rod:theoretical basis of mechanical model of DNA[M].Beijing:Tsinghua University Press，2006(in Chinese)

[16]张淑杰，李瑞祥，丁同才.盘绕式杆状展开机构的设计与力学分析[J].力学季刊，2006，27(2):341 －347

Zhang Shujie，Li Ruixiang，Ding Tongcai.Design and mechanical analysis of coilable lattice mast[J].Chinese Quarterly of Mechanics，2006，27(2):341 －347(in Chinese)

[17]Jiang D，Pierre C，Shaw S W.Large-amplitude non-linear normal modes of piecewise linear systems[J].Journal of Sound and Vibration，2004，272(3-5):869 －891

[18]张亚辉，林家浩.结构动力学基础[M].大连:大连理工大学出版社，2007

Zhang Yahui，Lin Jiahao.Fundamentals of structural dynamics[M].Dalian:Dalian University of Technology Press，2007(in Chinese)