飞机结构MSD失效概率的敏感性分析
杜永恩 王生楠
(西北工业大学 航空学院,西安710072)
可靠性分析是结构分析的重要内容,是评估结构安全性能的主要手段.概率方法是进行可靠性分析最精确也是最常用的方法,对各随机变量的联合概率分布函数在安全(失效)域内进行积分即可得到结构的安全(失效)概率.各随机变量对概率响应的影响不同,因此其在可靠性分析中的“重要性”也不同.通过概率敏感性分析,可以定量地分析各随机变量对概率响应的影响,进而确定可靠性分析中最“关键”的因素,作为结构设计和维护的重要参考依据.2006年起,文献[1-2]等开始了对概率敏感度的分析研究,定义了一种衡量失效概率对随机变量的敏感度概念,并给出了计算方法.2010年文献[3]通过概率敏感度分析对损伤容限分析的随机参数进行了重要性分类,并将该方法应用于T-38机翼分析.
广布疲劳损伤是影响老龄飞机结构完整性的重要因素.在同一元件上同时存在多条疲劳裂纹的情况称为多部位损伤(MSD,Multiple Site Dam-age),是导致广布疲劳损伤的重要源之一.通常对MSD结构进行寿命分析是通过裂纹萌生的S-N曲线分别确定各部位的裂纹萌生寿命,然后通过裂纹扩展分析得到结构的全寿命[4-11].MSD结构初始裂纹萌生的位置不同会对结构在给定寿命下失效概率产生影响,通过分析失效概率对不同部位裂纹萌生寿命对数均值和应力的敏感性可以量化各部位结构可靠性的影响,从而确定对结构安全最关键的部位.关于MSD结构疲劳损伤的概率敏感性分析,国内尚未见相关文献.本文通过定义核函数建立各应力集中位置裂纹萌生寿命对数均值和应力对失效概率的敏感性分析模型,采用Monte-Carlo模拟的方法计算概率敏感度.
1 概率敏感性
通常分析结构的失效概率是通过对各随机变量的联合概率密度函数在失效域进行积分得到:

式中,x为随机变量向量;g(x,t)为断裂准则确定的功能函数,g(x,t)≤0表示结构在使用时间为t时失效.定义函数:

则结构的失效概率为
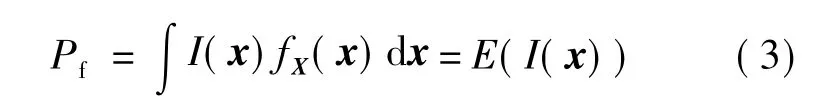
文献[1-2]通过结构失效概率对各随机参数的偏微分定义无量纲的概率敏感性因子为

该因子的物理意义为单位随机参数变化对应的失效概率的线性变化量.例如,随机参数 μi增加1%,则失效概率的增加量为

若各随机变量为独立分布的,则联合概率密度函数为

式中n为随机变量个数.则对于随机变量Xi所对应的参数θi,式(4)中的概率敏感性因子中的微分可通过下式计算:


式中κθi为一个核函数,定义如下:

该函数只与相应的随机变量xi及其参数θi有关,可对各随机变量分别独立计算.
Monte-Carlo模拟是结构疲劳可靠性分析的一种常用概率方法,通过确定性算法得到每个抽样的分析结果I(xj)(j=1,2,…,M),则对某随机变量xi的参数θi,其对失效概率的敏感性因子可通过下式得到:

式中M为Monte-Carlo模拟次数.该算法利用了概率分析的结果,只需在其上增加少许计算量即可得到失效概率对有关参数的概率敏感度.
2 MSD结构的概率敏感性分析
在MSD结构中,可能出现裂纹的位置定义为关键位置.设关键位置的个数为k个,每个关键位置的裂纹萌生寿命定义为该部位裂纹尺寸超过最小可检裂纹尺寸aini时的使用时间.在位置i,恒幅载荷下裂纹萌生的寿命公式为

式中,Ni为恒幅载荷循环数;σi为对应位置的最大应力;m和Ci是该位置的材料常数.在裂纹萌生的概率模型中,Ci为随机变量,其服从对数均值为μ,对数标准差为s的对数正态分布.
由式(10)可得

则各裂纹萌生寿命也服从对数正态分布,其概率密度函数为
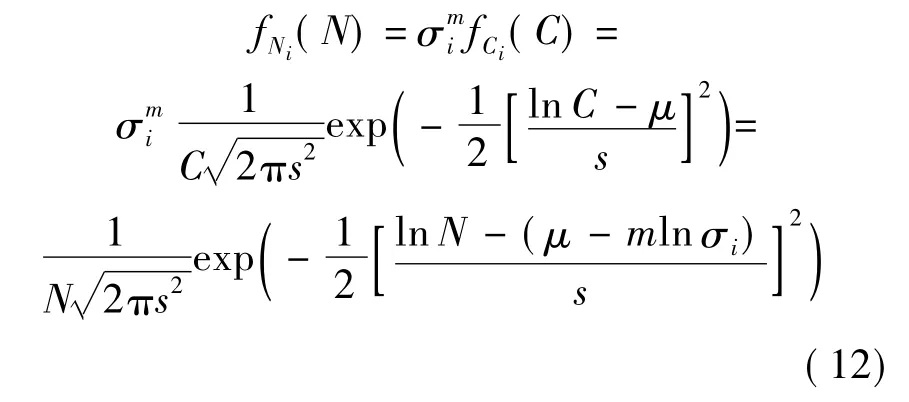
其对数均值为ωi=μ-mlnσi,对数标准差为s.
在材料确定的情况下,关键部位的应力大小是决定裂纹萌生寿命的关键因素,通过分析结构失效概率对各关键部位裂纹萌生寿命的对数均值ωi和应力σi的敏感性,可量化各位置对结构可靠性的影响,从而确定对结构安全影响最大的位置,为结构设计和改进提供参考.对于参数和σi,式(8)中核函数分别为

函数图像如图1和图2所示.

图1 最大应力核函数

图2 裂纹萌生寿命对数均值核函数
将式(13)代入式(9)中,即可得到失效概率对各部位萌生寿命对数均值和应力的敏感性,从而确定对可靠度影响最大的部位.
3 共线多孔板失效概率敏感性分析
采用以上提出的概率敏感性分析方法,选取飞机结构中易发生MSD的共线多孔板进行分析.算例的几何构形如图3所示,材料选用2027-T3铝合金,其主要材料性能值列于表1.对模拟试件两端施加σ=152.6 MPa的恒幅载荷,计算其在给定使用时间下的失效概率及其对可能出现裂纹位置初始应力和各裂纹萌生寿命对数均值的概率敏感度.

图3 共线五孔结构几何构形图

表1 主要的材料参数
各孔水平方向的左右边缘是可能出现裂纹的位置,将这些位置由左至右分别编号为1~10.通过有限元计算可得各位置最大应力和裂纹萌生寿命的对数均值为

通过Monte-Carlo模拟进行概率分析得到的在不同寿命下的结构失效累积概率如图4所示.

图4 累积失效概率
将Monte-Carlo模拟每次抽样的Xi和模拟结果I(Xi)代入式(13)和式(9)即可得失效概率对各部位应力和裂纹萌生寿命对数均值的敏感度.经计算得到给定寿命N=1.55×105时失效概率对各部位应力和裂纹萌生寿命对数均值的敏感度如表2所示(由于板的对称性,只选取部位1~5的数据进行分析)

表2 概率敏感度S
这表示当最大应力和裂纹萌生寿命的对数均值增加1%时,结构在N=1.55×105时失效概率提高S×0.01.由表2中可以看出失效概率随着最大应力的增大而提高,随着萌生寿命对数均值的增大而降低,这与实际情况是相符的.不同寿命下失效概率对各部位最大应力和裂纹萌生寿命对数均值的敏感度如图5和图6所示.

图5 失效概率对最大应力的敏感度

图6 失效概率对裂纹萌生寿命对数均值的敏感度
对比图5~图6中曲线可以看出失效概率对位置1(边缘孔外端)的最大应力和裂纹萌生的对数均值敏感度明显高于其他部位,而对其他各部位的敏感度大体相同,这说明该部位对结构的疲劳可靠度影响最大.在进行结构设计时,通过改善几何构型降低该部位应力水平或提高该部位强度达到提高结构可靠度的最大效果.
4 结论
1)通过分析MSD结构失效概率对不同部位裂纹萌生寿命对数均值和应力的敏感性可以量化各部位结构可靠性的影响,从而确定影响结构安全的最关键部位.
2)本文的共线多孔板模拟结构显示边缘孔外端的应力和裂纹萌生寿命对数均值对结构失效概率影响最大,是影响结构安全的最关键部位.
References)
[1]Millwater H R,Osborn W R.Probabilistic sensitivities for fatigue analysis of turbine engine disks[J].International Journal of Rotating Machinery,2006:28487-1-12
[2]Millwater H R.Universal properties of kernel functions for probabilistic sensitivity analysis[J].Probabilistic Engineering Mechanics,2009,24(1):89-99
[3]Millwater H R,Wieland D H.Probabilistic sensitivity-based ranking of damage tolerance analysis elements[J].Journal of Aircraft,2010,47(1):161-171
[4]Moukawsher E J,Grandt Jr A F,Neussl M A.Fatigue life of panels with multiple site damage[J].Journal of Aircraft,1996,33(5):1003-1013
[5]Silva L F M,Goncalves J P M,Oliveira F M F,et al.Multiplesite damage in riveted lap-joints:experimental simulation and finite element prediction[J].International Journal of Fatigue,2000,22(4):319-338
[6]Cherry M C,Mall S,Heinimann B.Residual strength of unstiffened aluminum panels with multiple site damage[J].Engineering Fracture Mechanics,1997,57(6):701-713
[7]Wang G S.Analysing the onset of multiple site damage at mechanical joints[J].International Journal of Fracture,2000,105(3):209-241
[8]Shkarayev S.Probabilistic method for the analysis of widespread fatigue damage in structures[J].International Journal of Fatigue,2005,27(3):223-234
[9]Shi P,Mahadevan S.Corrosion fatigue and multiple site damage reliability analysis[J].International Journal of Fatigue,2003,25(6):457-469
[10]王传胜,张建宇,鲍蕊,等.飞机结构多部位损伤发生的可能性分析[J].北京航空航天大学学报,2006,32(8):899-902
Wang Chuansheng,Zhang Jianyu,Bao Rui,et al.Reliability analysis on structures with multiple site damage[J].Journal of Beijing University of Aeronautics and Astronautics,2006,32(8):899-902(in Chinese)
[11]闫晓中,王生楠,黄汉超.飞机结构发生多处损伤的概率分析方法[J].机械强度,2012,34(6):881-885
Yan Xiaozhong,Wang Shengnan,Huang Hanchao.Probability analysis method for aircraft structures containing multiple site damage[J].Journal of Mechanical Strength,2012,34(6):881-885(in Chinese)

