基于有向无圈图的敏捷卫星姿态机动策略
唐忠兴 韩 潮
(北京航空航天大学 宇航学院,北京100191)
敏捷卫星对地观测姿态机动策略问题随着对地观测卫星的发展得到了新的关注.与传统对地观测卫星相比,敏捷卫星不仅具有侧摆方向上的机动能力,还具有俯仰方向,甚至偏航方向上的快速机动能力,能够实现快速、准确指向目标的特点.敏捷卫星具有多自由度姿态机动的特点,使得其工作模式更加复杂多样.面对较大的目标观测区域,敏捷卫星利用其俯仰+滚转的快速姿态机动能力,能够在同轨运行过程中多次扫描目标区域的不同子区域,进行同轨拼幅观测,从而完成对目标区域的扫描观测.面对多个点目标集中分布在一轨两侧的任务也面临同样的观测问题.
文献[1-2]对敏捷卫星的观测工作模式进行了研究,总结了各种工作模式的特点,但对其姿态机动策略问题的研究并没有涉及.
文献[3-11]针对敏捷卫星的成像调度问题做了较为系统的研究分析,针对一天或更长的任务周期,考虑每天、每轨成像时间约束,星上存储容量约束,能源消耗约束,载荷指向约束,以及姿态机动能力约束等约束条件,分别采用约束满足模型、混合整型规划模型、图论模型等进行建模与求解.同时对几种常见的求解算法的效率和特点进行比较分析.
利用图论模型对成像调度问题进行建模的优点是其形式简单,具有成熟高效的多项式时间求解算法.文献[3-4]应用图论的方法对敏捷卫星的成像调度进行了建模求解,但是,文献[3]只考虑了观测目标数目最大化,并不能切实反映覆盖收益最大化,且没有对机动时间消耗进行优化;而文献[4]对姿态机动时间只进行固定假设.
本文将目标的观测时间窗口离散化成一系列带有条带信息的时刻点,并应用一种时间序的有向无圈图来描述敏捷卫星的同轨拼幅观测和同轨多点连续观测两种工作模式的姿态机动策略问题,建立相应的有向无圈图论模型.通过求解该有向无圈图中的最优路径来获得所需要的问题的解决方案,即满足观测覆盖收益最大化同时机动时间消耗最小的姿态机动策略方案.
1 敏捷卫星对地观测工作模式
1.1 同轨拼幅观测
同轨多条带拼接成像工作模式是利用敏捷卫星快速姿态机动能力,使卫星实现同轨多次同向推扫拼接成像,扩大单轨观测范围[2,12].
图1形象地描述了敏捷卫星同轨拼幅观测工作模式,假设目标观测区域为ABCD,卫星观测载荷视场角为β,在t1,t2,t3时刻,通过姿态机动,分别对条带1~3进行推扫,从而完成对目标区域ABCD的同轨拼幅扫描观测.

图1 同轨3次拼幅观测空间示意图
如果目标区域更大,则需要考虑区域划分问题.如图2所示,以星下点轨迹为基线,两侧以幅宽d为距,把目标区域划分成1~6个子区域(条带),按照滚转方向依次对条带进行编号,Ii=1,2,…,6,每个子区域的起始扫描点和终止扫描点分别为,起始扫描时刻和终止扫描时刻分别为.星下点轨迹在目标区域外时也类似.区域目标的条带划分算法请参见文献[12].

图2 区域划分方式
1.2 同轨多点连续观测
点目标是可以通过一个载荷幅宽完成成像的目标.同轨多点连续观测成像工作模式是利用卫星的快速姿态指向能力,实现对分布较为集中的多个点目标的快速成像,主要适用于同轨内距离星下点轨迹较近的多个成像点的观测任务[2].
敏捷卫星同轨多点连续观测工作模式如图3所示,在卫星同一次轨道上时,有比较集中的多个点目标D1~D20,利用敏捷卫星在俯仰和滚转方向上的姿态快速机动能力,在t1~t13时刻,依次实现对点目标D1,D3,D4,D5,D7,D9,D12,D13,D14,D15,D16,D17,D20的成像.
进行敏捷卫星姿态机动优化策略求解之前,预先将区域目标划分成若干个条带,或将每个点目标转化成一个固定扫描时长的条带,因此,本文将敏捷卫星同轨拼幅观测问题和同轨多点连续观测问题经过划分条带的预处理,统一为敏捷卫星多条带观测姿态机动优化策略问题.

图3 同轨多点连续观测空间示意图
2 问题描述
2.1 已有资源
任务目标过境时段[ts,te].条带,数目n.本文所研究问题中,同轨拼幅观测问题的区域目标所划分的条带数目,以及同轨多点连续观测问题所处理的点目标数目都比较少,一般n不大于20.
2.2 设计参数
第i次所要观测条带的Ii,以及视轴指向所要观测条带观测点的时刻ti,其中i=1,2,…,i≤n.
2.3 约束条件
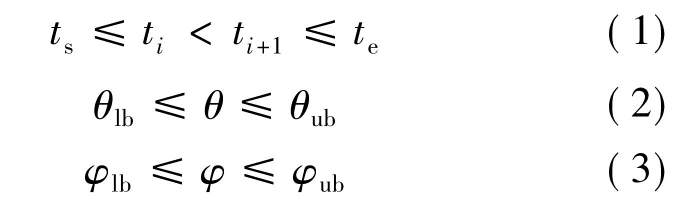
式中,θ为姿态机动完成后的滚转角;φ为姿态机动完成后的俯仰角;θup,θlb和φup,φlb分别表示滚转角和俯仰角的上下界.
考虑姿态机动能力和成像卫星的轨道高度,本文所研究问题的时间资源大约200 s左右,因此只考虑姿态机动能力约束.
2.4 优化目标
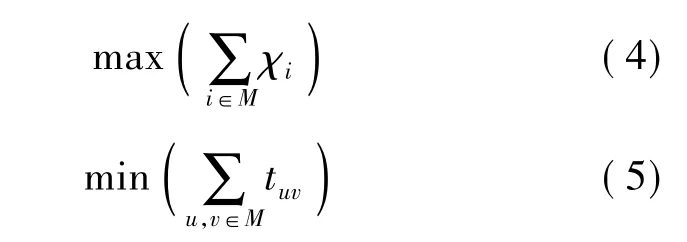
式中,在同轨拼幅观测模式下,χi为条带覆盖百分比,在同轨多点连续观测模式下,χi为点目标的权值.当优化目标(4)相同时,需要优化次优化目标(5),即姿态机动策略的机动时间消耗的总和.式(4)和式(5)中,集合M表示姿态机动策略所观测的条带编号集合.
3 问题求解
不同的起始机动时刻对应于不同的俯仰机动角度,为此,本文首先将各条带的可见时间段以一定的时间步长进行离散化.然后,利用这些带有条带信息标志的条带起始扫描时刻点为节点构造需要的时间序有向无圈图G(V,E,F),这样,将起始扫描时刻引入到机动时间的计算中,使得机动时间的影响更加符合实际应用.本文采用时间序有向无圈图的最优路径搜索方法进行求解.
3.1 时间序有向无圈图的构造
记时间序有向无圈图G(V,E,F),V为节点集,E为有向边集,F为边的权值,定义节点v(tob,I,χ)为各条带离散化的时刻即带有条带信息的起始扫描时刻,各个节点的条带信息包括条带编号I及条带覆盖百分比χ.将所有节点按起始扫描时刻tob的先后顺序进行排序,并添加两个虚拟节点分别表示源点s(0,-1,0)和汇点e(0,-2,0);对这些节点进行拓扑编号,s节点编号为0,依次递增到e节点,假设编号为Q(即共有Q+1个节点).定义guv为节点u和节点v之间的有向边,当u,v满足以下条件:
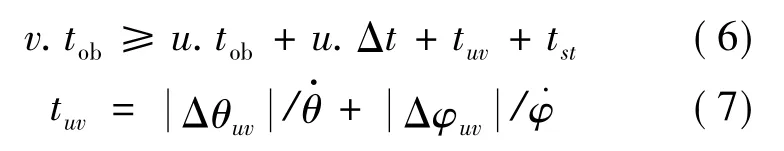
式中,guv相应的权值wuv为机动时间tuv;机动稳定时间tst在条带划分时与条带时长u.Δt进行综合考虑;和分别表示滚转角速度和俯仰角速度.在对条带进行划分时已经考虑了姿态最大机动角度约束式(2)和式(3),因此,图G中连通的路径即表明已满足姿态机动的约束条件.关于姿态机动滚转角Δθuv和俯仰角Δφuv的算法请参见文献[12].
定义一条从源点s开始,结束于节点v的路径P(L,C,{s,a1,a2,…,v}),L为路径P的长度,如式(4)所示,C为路径的消耗,如式(5)所示,{s,a1,a2,…,v}为路径P的各个节点.
敏捷卫星多条带观测姿态机动策略优化问题的求解转换为在图G(V,E,F)中,寻找一条从源点s到汇点e的最优路径p,即长度最长的路径,同时满足路径中各个节点的条带编号I不重复,即每个条带目标最多扫描观测一次.这里,需要对终止于同一节点的“优路径”进行定义.
定义1“优路径”:对终止于节点j的两条路径:p(Lp,Cp,{s,ap1,ap2,…,j},q(Lq,Cq,{s,aq1,aq2,…,j}).
当满足以下条件之一时,路径p优于路径q,即路径p是优路径:

表明路径长度更长,观测覆盖收益更大;当路径长度相等时,路径消耗更小,机动时间消耗更小.
3.2 最优路径搜索流程
应用图论中的Dijkstra算法的思想[13]进行最优路径搜索,从源点s出发,依照节点的拓扑编号次序,扩展路径到其可行的后续节点,并不断更新从源点s到各个节点的最优路径,最终获得从源点s到汇点e的最优路径.
图4给出基于时间序有向无圈图的最优路径搜索流程图.
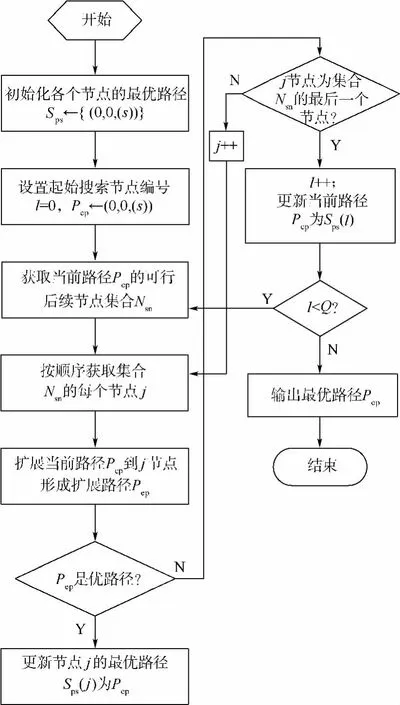
图4 最优路径搜索流程图
4 仿真算例
本节通过两个算例来仿真验证敏捷卫星多条带观测姿态机动策略算法的有效性和可行性.
4.1 同轨拼幅观测算例
4.1.1 初始条件
纪元时刻:2012-01-01T12:00:00.
任务目标过境时段:

目标区域:由表1中7个点围成的多边形区域.

表1 目标区域
轨道:半长轴a=7078140.000 m,偏心率e=0.0,轨道倾角iic=98.188°,升交点赤经Ω=101.389°,近地点幅角ω= 0.0°,平近点角M=0.0°.
姿态机动能力:俯仰 ± 35°,滚转 ± 30°,角速度 3 (°)/s.
载荷视场角:4°.
离散时间步长:0.5 s.
4.1.2 仿真结果
表2给出了最优路径结果.根据表2的最优路径结果,算法给出的姿态机动策略如图5所示,表现姿态滚转角和俯仰角的变化过程,可以看出,策略满足姿态机动能力约束.时间轴以第1次开始机动时刻为基准.相应的仿真结果二维视图如图6所示,显示了卫星在轨运行对目标的观测情况,仿真结果验证了本文算法的可行性.

表2 同轨拼幅观测算例最优路径结果
由表3的仿真结果可以看出,进行同轨拼幅观测姿态机动策略后,覆盖百分比得到了很大的提升,从16.43%提升到了99.083%,接近100%全部扫描覆盖目标区域.

图5 同轨拼幅观测算例姿态机动策略
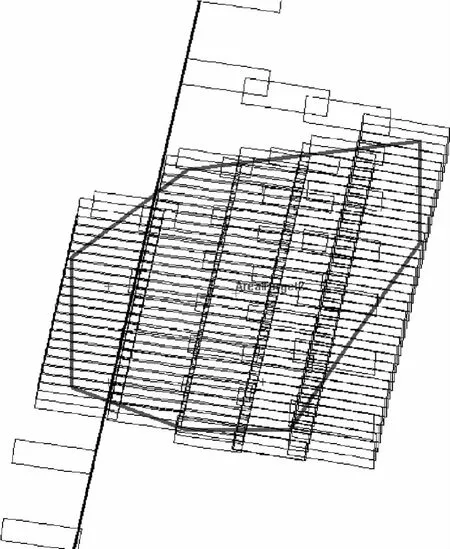
图6 同轨拼幅观测算例仿真结果二维视图

表3 累积覆盖百分比比较 %
4.2 同轨多点连续观测算例
4.2.1 初始条件
纪元时刻,轨道,姿态机动能力,载荷视场角,离散时间步长等参数,与4.1.1节的参数相同.其他不同的参数如下.
任务目标过境时段:
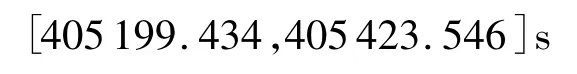
点目标:表4中的20个点目标,权值全为1;
点目标扫描时长:2.0 s.
4.2.2 仿真结果
表5给出了最优路径结果.图7是相应的机动策略.图8显示了仿真结果的二维视图.
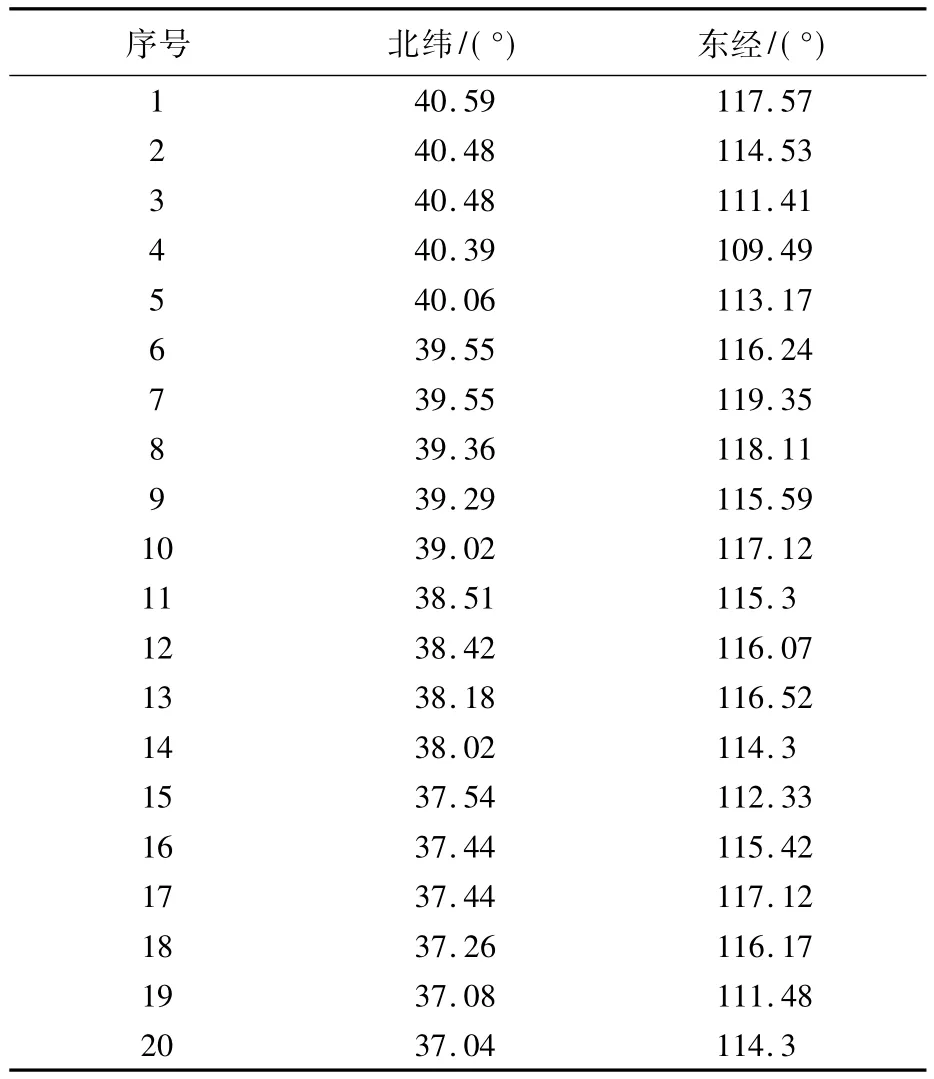
表4 点目标列表

表5 同轨多点连续观测算例最优路径结果
由表6的仿真结果可以看出,通过预置侧摆角度,可以观测到的点目标数目为4,而进行同轨多点连续观测姿态机动策略后,观测点目标数目得到了很大的提升,扫描观测了全部点目标.

表6 观测点目标数目比较

图7 同轨多点连续观测算例姿态机动策略

图8 同轨多点连续观测算例仿真结果二维视图
为了对算法的计算效率进行分析,分别对5,10,15,20个点目标进行姿态机动策略计算,离散时间步长分为 0 .5,1.0,2.0,4.0 s,计算结果都能够完成所有目标的观测,相应的计算时间和机动消耗时间结果如表7所示,计算条件是Inter i5 2.4 GHz,RAM 6 GB 的PC机.
从表7可以看出,随着离散度的细化以及目标数目的增加,计算消耗时间呈指数增加,而机动消耗时间随着离散度的细化,能够得到一定的改善.
本文处理的目标数目较少,一般不大于20个目标,考虑计算效率,可以采用2.0s或4.0s的离散度,既能保证观测目标数目,机动消耗时间也不会增加太多,而且计算时间较短.
采用文献[12]的基于粒子群算法分段优化的敏捷姿态机动策略,对两种模式的算例进行计算,与本文采用的方法进行比较,其中粒子群算法的种群规模为10,种群代数为100,结果如表8所示.
从表8可以看出,对于同轨拼幅观测模式的算例,二者结果相差不多.对于同轨多点连续观测模式的算例,本文算法能够提升优化目标.

表7 不同离散度时算法计算效率s

表8 文献[12]方法和本文方法结果比较
从上面的仿真算例和分析可以看出,敏捷卫星多条带观测姿态机动策略算法能够实现对目标区域的同轨拼幅观测,较大地提升了对目标区域的覆盖百分比;能够实现对多点目标的连续观测,较大地提升了观测点目标数目,说明了本文提出的敏捷卫星多条带观测姿态机动策略算法在敏捷卫星对地观测任务应用中的可行性.
5 结论
1)本文提出的基于时间序有向无圈图的敏捷卫星多条带观测姿态机动策略算法能够有效求解敏捷卫星同轨拼幅观测、同轨多点连续观测两种工作模式的成像问题.
2)算法的求解结果和求解效率与模型的离散度有关.一方面,算法的求解结果随着离散化程度的细化而改善;另一方面,算法的求解效率随着离散度的细化而下降,特别是当目标数目规模较大的情况更加明显.因此应合理选择离散度.
3)与采用粒子群算法的分段优化的算法相比,本文采用的算法表现更优.
4)本文研究为敏捷卫星的成像任务应用提供了一个简便而有效的姿态机动策略算法.
References)
[1]Baudoin A.Beyond spot 5:pleiades,part of the French-Italian program orfeo[C]//The 20th Int Archives Photogrammetry and Remote Sensing Congr.Istanbul,Turkey:ISPRS,2004:260-267
[2]张新伟,戴君,刘付强.敏捷遥感卫星工作模式研究[J].航天器工程,2011,20(4):32-38
Zhang Xinwei,Dai Jun,Liu Fuqiang.Research on working mode of remote sensing satellite with agile attitude control[J].Spacecraft Eengineering,2011,20(4):32-38(in Chinese)
[3]Gabrel V,Moulet A,Murat C,et al.A new single model and derived algorithms for the satellite shot planning problem using graph theory concepts[J].Annals of Operations Research,1997,69:115-134
[4]Mancel C,Lopez P.Comlex optimization problems in space systems[C]//13th International Conference on Automated Planning&Scheduling(ICAP'03).Trento,Italy:ICAP,2003:1-5
[5]Li Y,Xu M Q,Wang R X.Scheduling observations of agile satellites with combined genetic algorithm[C]//Third International Conference on Natural Computation.Piscataway,NJ:IEEE,2007,3:29-33
[6]陈英武,白保存,贺仁杰,等.遥感卫星任务规划问题研究现状与展望[J].飞行器测控学报,2008,27(5):1-8
Chen Yingwu,Bai Baocun,He Renjie,et al.A survey on mission planning for remote sensing satellites[J].Journal of Spacecraft TT&C Technology,2008,27(5):1-8(in Chinese)
[7]王钧,陈慧中,左怀玉,等.基于时间序有向图的对地观测卫星成像预调度[J].兵工学报,2008,29(5):608-614
Wang Jun,Chen Huizhong,Zuo Huaiyu,et al.Pre-scheduling for imaging requests of earth observing satellites based on time ordered acyclic directed graph[J].ACTA Armamentarii,2008,29(5):608-614(in Chinese)
[8]Wang P,Reinelt G,Gao P,et al.A model,a heuristic and a decision support system to solve the scheduling problem of an earth observing satellite constellation[J].Computers&chemical Engineering,2011,61(2):322-335
[9]Romain G B,Gabrel V,Antoine F.Building a really executable plan for a constellation of agile earth observation satellites[EB/OL].[2013-06-18].http://www.congrex.nl/11c05/Papers/GrassetBourdel_paper.pdf
[10]Wu G H,Liu J,Ma M H,et al.A two-phase scheduling method with the consideration of task clustering for earth observing satellites[J].Computers&Operations Research,2013,40(7):1884-1894
[11]Beaumet G,Gabrel V,Charmeau M C,et al.Feasibility of autonomous decision making on board an agile earth-observation satellite[J].Computational Intelligence,2011,27(1):123-139
[12]唐忠兴,韩潮.敏捷卫星同轨拼幅观测姿态机动策略研究[C]//第一届高分辨率对地观测学术年会——卫星遥感与应用优秀论文集.北京:高分辨率对地观测学术委员会,2012:3-14
Tang Zhongxing,Han Chao.Study on the attitude maneuver strategy for the agile satellite in one-orbit strips-jointed observation mode[C]//The 1st High Resolution Earth Observation Annual Conference:Satellite Remote Sensing and Application.Beijing:HREOAC,2012:3-14(in Chinese)
[13]王桂平,王衍,任嘉辰.图论算法理论、实现及应用[M].北京:北京大学出版社,2011:131-147
Wang Guiping,Wang Yan,Ren Jiachen.Graph theory,implement and application[M].Beijing:Peking University Press,2011:131-147(in Chinese)

