悬浮月尘的遮挡模型
陈 阔 李 娜 冯华君 徐之海
(浙江大学 现代光学仪器国家重点实验室,杭州310027)
人类在月球表面的活动会致使月尘悬浮,尤其是月球探测器的着陆和行进[1].由于月尘颗粒的形状不规则性以及其静电性[2],它在光电器件表面的附着以及在其工作空间的悬浮会造成严重的设备性能和效率的降低.国内外对附着月尘的遮挡模型进行了不同的研究[3-5],文献[1]最早提出了附着月尘对光电器件的单粒度遮挡模型,并将其拓展到多粒度遮挡模型,文献[5]提出附着月尘的简化模型,并研究了对太阳能电池的遮挡影响.同理,当月尘悬浮在光电器件的工作光路中时,必然会对光能量产生衰减,因此,研究悬浮月尘对光电器件的遮挡效应非常必要.
1 附着月尘的遮挡
文献[1]提出的附着月尘的遮挡示意图,如图1所示.

图1 附着月尘的遮挡模型示意图
月尘附着在某光电器件的光学表面上,光学表面的有效工作面积为A,月尘颗粒的受光面积为α,颗粒总数为N,平均光吸收率为γ,它表征了月尘颗粒的散射能力,可通过实验手段测量[1].易知光电器件的光学表面上某点未被遮挡的概率为P=(1-γα/A)N,为简化运算引入无量纲变量j=A/(γα),得
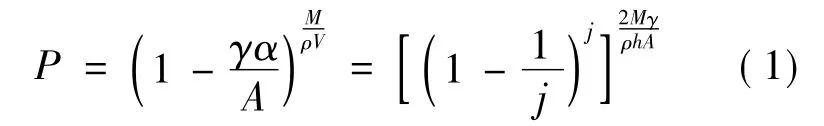
式中,M为月尘颗粒的总质量;ρ为月尘颗粒的体密度;V为单颗月尘的体积;h为月尘颗粒在垂直光学表面方向上的平均高度,是统计平均值,其误差取决于采样月尘颗粒的数目.
为衡量附着月尘对光学表面的遮挡影响,可利用光学表面前后光照度的变化量,因此设图1中光学表面前方入射光的光照度为Ei,光学表面后方出射光的光照度为Eo,继而得
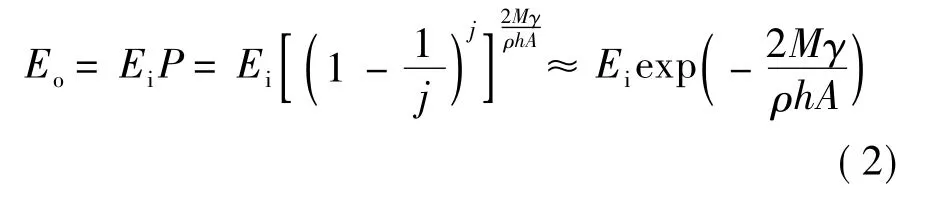
式中,由于A≫α,即满足j→+∞,此时指数函数关系成立.
综上所述,建立了附着月尘的遮挡模型,当已知光电器件的有效工作面积、附着月尘的总质量、月尘颗粒的体密度、垂直光学表面方向上的平均高度、平均光吸收率这5个物理量时,可计算月尘颗粒附着在光电器件的光学表面上时,该光学表面的透过率τ:

2 悬浮月尘的遮挡
2.1 单粒度遮挡模型
基于附着月尘的遮挡模型,本文建立了悬浮月尘的遮挡模型,其工作结构如图2所示.在立体空间内均匀悬浮着质量为M的月尘颗粒,光线从立体空间-z的方向入射,沿+z方向出射,记立体空间的z方向(光照方向)长度为l,垂直于z方向的横截面的面积为A.

图2 悬浮月尘的遮挡模型示意图
考虑月尘颗粒为单粒度颗粒群,其粒度大小为d,α=π(d/2)2.考虑月尘颗粒在立体空间内x,y,z3个方向上的运动是随机的,且假设立体空间内存在垂直于z方向的某一横截面S,那么单颗月尘对该横截面的遮挡概率为α/A,又知单颗月尘恰好落在横截面S上的概率是d/l,因此立体空间内某点未被单颗月尘遮挡的概率p为

它的物理意义是:保持立体空间的体积不变,将其在x,y方向上拉伸l/d倍,在z方向上压缩到单颗月尘的粒度d,形成由l/d个面积为A的小平面拼成的大平面L,它未被单颗月尘遮挡的概率也是p.
同理得到大平面L上某点未被N颗单粒度月尘颗粒所遮挡的概率PL为

如果再次将大平面L还原为立体空间,并令此立体空间某点未被N颗单粒度月尘颗粒遮挡的概率为Ps,且它不等于PL.因为若在某一光线上同时存在多于一颗月尘颗粒,它们之间必然会发生遮挡,但是由于月尘颗粒的散射效应[6-7],前一颗月尘的散射光不会完全被后一颗月尘遮挡.为描述散射效应在遮挡模型中的影响,本文引入反向修正因子κ,将Ps表达为

参考式(1)、式(2)的简化过程,同样引入式(7)所示的无量纲变量j,将其代入式(6)可简化Ps,因此得到单粒度悬浮月尘对立体空间遮挡时,该立体空间的透过率为

式中,月尘参数M和ρ同附着月尘的遮挡模型,利用立体空间的透过率可衡量悬浮月尘对立体空间的遮挡影响.
2.2 多粒度遮挡模型
事实上,月球表面与地球完全不同的大气环境和土壤环境等使月尘具有独特的成分、颗粒形状和尺寸,根据NASA的资料,月尘的粒度大小从1 μm分布到1000 μm[8-10],因此单粒度的遮挡模型不能完全准确地描述悬浮月尘对立体空间的遮挡影响,需根据月尘的粒度分布特性,建立多粒度悬浮月尘的遮挡模型.
如图2所示,立体空间内悬浮的多粒度月尘颗粒的总质量为Mtotal,假设有n种粒度的月尘颗粒,粒度大小分别为d1,d2,…,di,…,dn;颗粒个数分别为N1,N2,…,Ni,…,Nn;相应的受光面积分别为α1,α2,…,αi,…,αn,令多粒度月尘颗粒的平均粒度为¯d,可将式(6)拓展到多粒度模型,得到立体空间内某点未被多粒度月尘颗粒遮挡的概率为

同理定义式(10)所示的无量纲变量ji,式中i=1,2,…,n代表第i种粒度的月尘颗粒.将式(10)代入式(9)化解,并设粒度大小为di的月尘颗粒质量为Mi,得到立体空间内某点未被多粒度月尘颗粒遮挡的概率为

若已知多粒度月尘颗粒的粒度分布函数,或通过测量等手段得到,并记为F(di),那么可计算在该粒度分布下月尘的归一化质量为

式中Vi表示粒度大小为di的单颗月尘的体积.根据粒度分布函数的概念,结合式(11)和式(12),可计算多粒度悬浮月尘对立体空间遮挡时,该立体空间的透过率为

综上所述,本文建立了悬浮月尘的遮挡模型,通过计算指定立体空间的透过率来衡量悬浮月尘的遮挡量.经测量或已知月尘颗粒的粒度分布后,采用多粒度遮挡模型可准确地计算悬浮月尘的遮挡量,若未知粒度分布函数,亦可利用单粒度遮挡模型近似计算.
3 实验及结果
3.1 悬浮月尘遮挡的仿真实验
为分析月尘环境下,悬浮月尘对光电器件的遮挡影响,本文建立了分析悬浮月尘遮挡影响的物理仿真实验环境,实验装置如图3所示.实验月尘采用根据美国宇航局的资料数据制作的模拟月尘[11-12],光源采用照度恒定的灯箱,光照度的测量采用标准的照度测量仪.本文设计了内部立体空间体积为8 cm×8 cm×25 cm的透明玻璃组件,它的作用是使月尘在该立体空间内悬浮,从而模拟月球表面上的悬浮月尘.

图3 悬浮月尘遮挡的仿真实验装置
本文悬浮月尘的仿真遮挡实验分为以下4个步骤:
1)开启恒定灯箱,当玻璃组件内为空时,读取照度测量仪读数,记为Ei;
2)取质量为M的月尘颗粒,放在玻璃组件内并开启玻璃组件,令内部的月尘悬浮,待月尘颗粒稳定悬浮后再次读取照度测量仪的读数,并记为Eo;
3)重复步骤2)k次,最后得到被测月尘的质量分别为M1,M2,…,Mk时,照度测量仪的读数依次为Eo1,Eo2,…,Eok;
4)根据式(8)和式(13)计算总共k次实验中,立空间的透过率τo1,τo2,…,τok.
本文设计了3组悬浮月尘的仿真实验,采用平均粒度为281 μm,292 μm,304 μm的模拟月尘,分别进行6次测试,得到6组不同悬浮密度下立体空间的透过率,如图4~图6所示,其中ρv为立体空间内的月尘悬浮密度,τ为在8 cm测量距离处的立体空间透过率.

图4 悬浮月尘仿真实验1结果

图5 悬浮月尘仿真实验2结果

图6 悬浮月尘仿真实验3结果
从图4~图6中可以看到,实验1的典型测量结果为当月尘的悬浮密度达到3.58 mg/cm3时,立体空间透过率为0.545;实验2的典型测量结果为当悬浮密度达到3.89 mg/cm3时,透过率为0.504;实验3的典型测量结果为当悬浮密度达到4.02 mg/cm3时,透过率为0.518.当立体空间的透过率下降到0.5时,可理解为此时悬浮月尘颗粒的遮挡量,相当于在立体空间内放置了一块透过率为0.5的滤光片,使其通光能量衰减一半.
3.2 结果及分析
已知模拟月尘的粒度分布函数[1]为F(d)=3/d4,那么分别通过式(8)和式(13)计算悬浮月尘单粒度、多粒度遮挡模型中立体空间的理论透过率,其中月尘的体密度ρ以及归一化质量Mdist根据美国宇航局的月尘参数,分别取值3.01 g/cm3和3.25×10-5μg.
本文提出的反向修正因子κ,实质是衡量悬浮月尘颗粒的散射作用,因月尘颗粒维度远大于光波长从而发生米氏散射.由于月尘颗粒数目较多,可使用统计平均值来表征月尘的该项特征,这与使用平均光吸收率[1]表征附着月尘的透过率原理相同.
利用仿真实验中的模拟月尘参数,计算单粒度模型中立体空间的理论透过率与月尘悬浮密度的关系,以及多粒度模型立体空间的理论透过率与月尘悬浮密度的关系,理论计算结果参见图4~图6.
在3组仿真实验中,理论模型中的反向修正因子κ取定值0.39,实验选择了不同粒度的月尘颗粒,并且理论结果都能较好地与仿真实验数据相吻合.这说明,使用0.39作为表征月尘颗粒散射作用的统计平均值时,本文提出的悬浮月尘的遮挡模型能准确地表达月尘的悬浮密度与立体空间透过率的关系.同时多次仿真实验检验了反向修正因子κ的稳定性,进而验证了本文提出的悬浮月尘的遮挡模型的正确性与可靠性.
根据本文的悬浮月尘的遮挡模型,被测立体空间内,当悬浮月尘的密度等于1 mg/cm3时,在测量距离为8 cm处,它对光电器件的遮挡率约为10%~20%,可认为此时光电器件能够正常工作;当悬浮月尘的密度增大为10 mg/cm3时,在测量距离为8 cm处,它对光电器件的遮挡率约为80%~90%,那么认为此时光电器件已经不能正常工作.利用本文的悬浮月尘遮挡模型,能够对月尘影响下的光电器件的工作性能做出恰当的评估.
4 结论
本文通过理论分析和仿真实验,研究了立体空间内悬浮月尘的遮挡.结果表明:
1)测量光路中月尘的悬浮密度,可计算月尘对光能量的遮挡量大小;
2)光路中光能量的相对透过率随月尘悬浮密度的增加呈指数衰减的趋势;
3)悬浮月尘遮挡模型能对光电器件的能量利用率进行评估,进而有效地避免月尘带来的重大影响和灾害.
本课题的下一步研究工作是分析月尘的散射理论、复杂形状因子以及波长选择性,并拓展月尘遮挡模型.
References)
[1]Katzan C M,Edwards J L.Lunar dust transport and potential interactions with power system components[R].NASA-CR-4404,1991
[2]Walton O R.Adhesion of lunar dust[R].NASA/CR—2007-214685,2007
[3]Gaier J R.The effects of lunar dust on EVA systems during the Apollo missions[R].NASA/TM 213610,2005
[4]Katzan C M,Stidham C R.Lunar dust interactions with photovoltaic arrays[C]//Frederik C K.Photovoltaic Specialists Conference,Conference Record of the Twenty Second IEEE.Las Vegas,NV:IEEE,1991,2:1548-1553
[5]庄建宏,王先荣,冯杰.月尘对太阳电池的遮挡效应研究[J].航天器环境工程,2010,27(4):409-411
Zhuang Jianhong,Wang Xianrong,Feng Jie.Overlapping effect of lunar dust sediment on solar cell[J].Spacecraft Environment Engineering,2010,27(4):409-411(in Chinese)
[6]王雪艳.基于米氏散射理论的粒度测试算法研究[D].西安:西安工业大学,2011
Wang Xueyan.Research on particle size test algorithm based on Mie theory[D].Xi’an:Xi’an Technological University,2011(in Chinese)
[7]杨娟.悬浮颗粒数的质量分布信息模型及其应用[D].南京:南京理工大学,2008
Yang Juan.The mass distribution information model and application for aerosol counting[D].Nanjing:Nanjing University of Science and Technology,2008(in Chinese)
[8]CarrierrⅢ W D.Particle size distribution of lunar soil[J].Journal of Geotechnical and Geoenvironmental Engineering,2003,129(10):956-959
[9]CarrierⅢ W D.Lunar soil grain size distribution[J].The Moon,1973,6(3/4):250-263
[10]Gromov V.Physical and mechanical properties of lunar and planetary soils[J].Earth Moon and Planets,1998,80(1/3):51-72
[11]李蔓,童靖宇,沈志刚,等.模拟月尘制备及其物理和力学性质研究[J].航天器环境工程,2012,29(5):532-535
Li Man,Tong Jingyu,Shen Zhigang,et al.Preparation and mechanical properties of lunar simulant[J].Spacecraft Environment Engineering,2012,29(5):532-535(in Chinese)
[12]姚日剑,王先荣,王鹚.月球粉尘的研究现状[J].航天器环境工程,2008,25(6):512-515
Yao Rijian,Wang Xianrong,Wang Yi.A revier on lunar researches[J].Spacecraft Environment Engineering,2008,25(6):512-515(in Chinese)

