六边形孔蜂窝梁挠度的实验与有限元分析

张春玉,　沈　岩,　赵延林,　宋海通

(黑龙江科技大学 建筑工程学院, 哈尔滨 150022)



六边形孔蜂窝梁挠度的实验与有限元分析

张春玉,沈岩,赵延林,宋海通

(黑龙江科技大学 建筑工程学院, 哈尔滨 150022)

以研究蜂窝梁的挠度特征及其计算方法为目的,设计扩张比k=1.65的六边形开孔蜂窝梁,利用实验与有限元软件ANSYS探讨简支蜂窝梁在均布荷载作用下的挠度变化,获得了蜂窝梁的挠度变化规律、破坏特征,并将实验、有限元模拟及我国《钢结构设计规范》征求意见稿给出的挠度公式,三者得出的临界荷载进行对比。结果显示,实验及有限元模拟的结果与规范公式计算结果相差5%～10%,表明规范计算公式具有足够的计算精度。文中采用的ANSYS实体建模方法可以用于蜂窝梁的研究。

蜂窝梁; 挠度; 实验; 有限元分析

0　引　言

蜂窝梁是在实腹工字钢或热轧H型钢的腹板上按一定的连续折线或弧线进行切割、首尾错位组装、焊接而成,是带有一系列孔洞的空腹钢梁。蜂窝梁通过改变截面形式充分提高了钢材的利用效率。与原型实腹工字钢梁相比,蜂窝梁不仅大幅度提高了抗弯刚度,同时钢材用量可节约25%～30%,可降低总的造价15%左右[1]。因此,蜂窝梁被广泛应用于厂房、车库、体育馆、火车站、轮船、桥梁及吊车桥架等工程[2]。蜂窝梁的挠度是反映其整体受力性能的重要指标,通过挠度可以充分了解其刚度特征。国内外一些学者或提出估算法[3],或采用有限元法[4-6],或推导出精确的挠度计算公式[7-8],对蜂窝梁的挠度计算方法进行大量的研究,但很少有人利用实验手段进行研究。为促进我国蜂窝梁设计的规范化,文中利用实验与有限元软件ANSYS模拟分析相结合的方法,将实验、有限元模拟及GB 50017—2012《钢结构设计规范》征求意见稿中蜂窝梁挠度计算公式(F.0.2-11)[9],三者得到的临界荷载进行对比,验证规范给出的挠度公式及ANSYS实体模型SOLID92用于蜂窝梁研究的准确性与适用性。

1　实　验

运用实验手段，研究较大扩张比(k=1.65)的简支蜂窝梁在分级均布荷载作用下沿梁长的挠度变化规律,并与当量实腹梁和原型实腹梁在蜂窝梁临界荷载作用下的挠度进行对比,分析蜂窝梁由于腹板开孔引起的截面削弱对其挠度的影响。

1.1试件设计

采用工字钢I16,钢材的强度等级Q235,六边形开孔,跨度总长(包括安全距离和支座加劲肋宽)2 768 mm,扩张比(蜂窝梁的截面高度H与原型实腹梁的截面高度h之比)k=1.65,开孔数为6,孔间距(相邻两个六边形孔中心点的水平最短距离)360 mm,六边形边长120 mm,蜂窝梁截面尺寸:H×b×dw×d=264 mm×88 mm×6 mm×9.9 mm,其中,b为翼缘宽度,dw为腹板厚度,d为翼缘平均厚度。

蜂窝梁采用简支约束,为了防止边孔因局部剪力过大而首先破坏,在两侧支座处均设置了宽为10 mm的支座加劲肋,并保证边孔最外侧的内角顶点距离支座处的水平最短距离hb≥H,取hb=H=264 mm。为了避免试件在加载过程中产生支座滑移发生危险,在支座加劲肋两侧向外水平方向各预留90 mm的安全距离。

1.2实验方案

沿梁长布置四处侧向支撑,以保证试件在加载过程中不会出现平面外位移,或发生扭转和整体失稳。实验通过三层分配梁在蜂窝梁上翼缘的八点进行加载,模拟均布荷载的实际情况。加载点沿梁长均匀布置,其中，第一层分配梁一根,第二层分配梁两根,第三层分配梁四根,上下层分配梁之间及分配梁与试件之间的荷载通过滚轴来实现传递,简支约束通过滚轴和固定轴来实现。实验加载装置如图1所示。

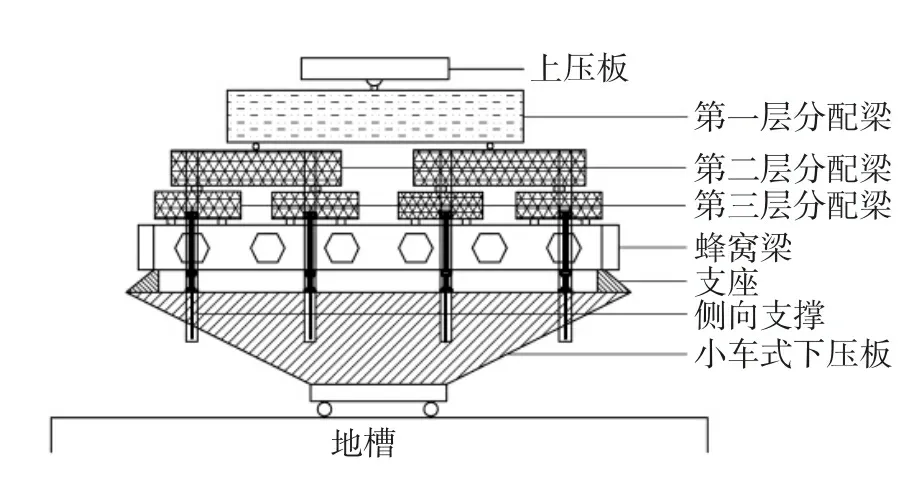
图1　实验加载装置

蜂窝梁的挠度利用百分表测量,简支梁在均布荷载作用下通常在跨中处的挠度最大,此处的挠度也最能反映梁的整体工作性能[10]。由于实验采用扩张比k=1.65的蜂窝梁,由文献[11]可知,开孔对腹板截面的削弱作用较明显,为研究剪切变形对蜂窝梁挠度的影响程度,在边孔和边孔相邻孔处也布置了百分表。在加载过程中，为准确测量试件的实际挠度,必须考虑支座位移对试件挠度的影响。百分表布置如图2所示。

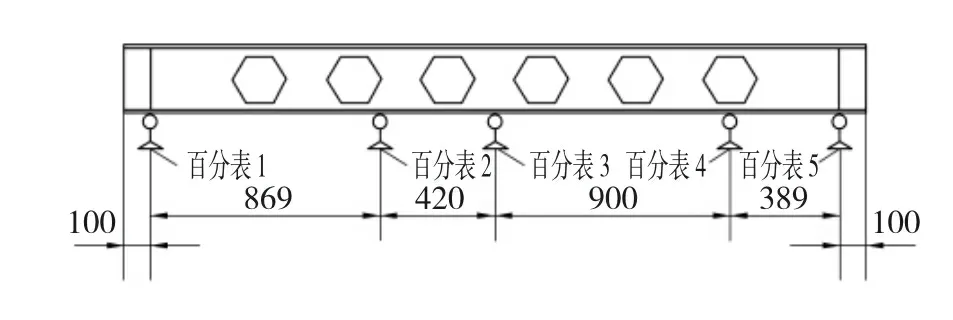
图2　百分表布置

实验采用微机控制电液伺服压力机,加载全过程由专业人员对计算机电液伺服系统进行控制。为使实验各部分具有良好的接触，检查实验仪器仪表是否正常工作及装置是否可靠,在试件正式加载前,取试件理论极限荷载的8%对试件进行预压。实验采用分级加载,每一级加载结束后,稳压4 min,待百分表读数稳定并记录后再进行下一级加载。为研究该蜂窝梁后期的承载能力和变形能力,当试件发生屈服后,仍继续对其加载,直至蜂窝梁破坏时终止实验。

1.3实验现象和数据

试件加载时采用分级荷载控制制度,每级加载增量为4 kN,加载后期每级荷载增量为2 kN。随着荷载的增加,百分表的读数逐渐变大。在加载1～12级即4～48 kN时,蜂窝梁没有发生直观的变形;在加载13～15级即52～60 kN时,梁左侧边孔的翼缘出现波浪形的变形,随后右侧边孔及各加载点处也出现波浪形变形,并且随着荷载的增加,波浪形变形和跨中挠度明显增大,此时每级荷载增量改为2 kN。当荷载加至65.4 kN时,百分表3的读数持续快速增加,试件两边边孔发生显著的剪切变形。此时,认为蜂窝梁已达到屈服,跨中最大挠度为10.130 mm。对蜂窝梁继续进行加载,观察蜂窝梁发生屈服后的挠度变化特征。当荷载加至67.8 kN时,百分表3的读数已无法稳定,蜂窝梁产生较大的挠曲变形,梁左端边孔六边形边线交接位置有两处出现撕裂现象,两边孔上方的第三层分配梁在竖直面内发生明显的转动。考虑到实验人员和仪器的安全,终止实验,最终跨中最大挠度为12.045 mm。

2　有限元模拟

利用有限元软件ANSYS建立与实验构件参数相同的模型,单元类型采用实体单元SOLID92,其具有大变形、大应变、塑性、蠕变和应力刚化等功能,非常适合模拟形状不规则的结构。利用SOLID92进行实体建模,可运用倒圆角等命令使所建模型充分接近蜂窝梁的实际形状。

建立蜂窝梁三维模型时,采用自底而上和自顶而下两种相结合的方式,钢材的弹性模量E=206 GPa,泊松比μ=0.3,应力应变关系采用双折线曲线,钢材塑性阶段的斜率取弹性模量的1/30。建模时忽略焊缝及残余应力的影响,有限元模型考虑了几何非线性和材料非线性。考虑几何非线性,可以准确分析材料的大变形;考虑材料的非线性,可以较详细地分析弯矩和剪力共同作用下的构件挠度变化特征[12]。单元划分采用自由网格划分的方式,支座为简支约束,通过对梁一端的下翼缘约束水平、竖向及侧向三个方向的位移，对另一端约束竖向位移和侧向位移加以实现。并对蜂窝梁翼缘施加侧向约束,这是为了防止构件在荷载作用下发生整体失稳。有限元模型如图3所示。

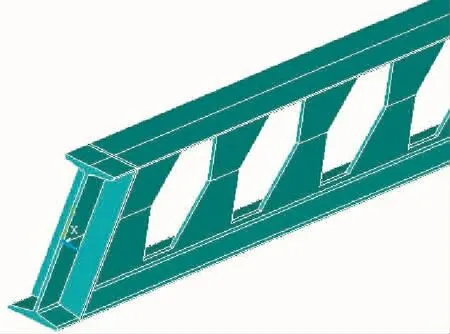
图3　有限元模型

文中采用的荷载为面荷载,大小为750 kN/m2,为精确得到蜂窝梁在允许挠度[v]=10.312 mm时的荷载情况,设置2 500子步对模型进行加载。

3　实验与有限元结果分析

实验研究和有限元分析得出的蜂窝梁荷载-跨中挠度曲线如图4所示。

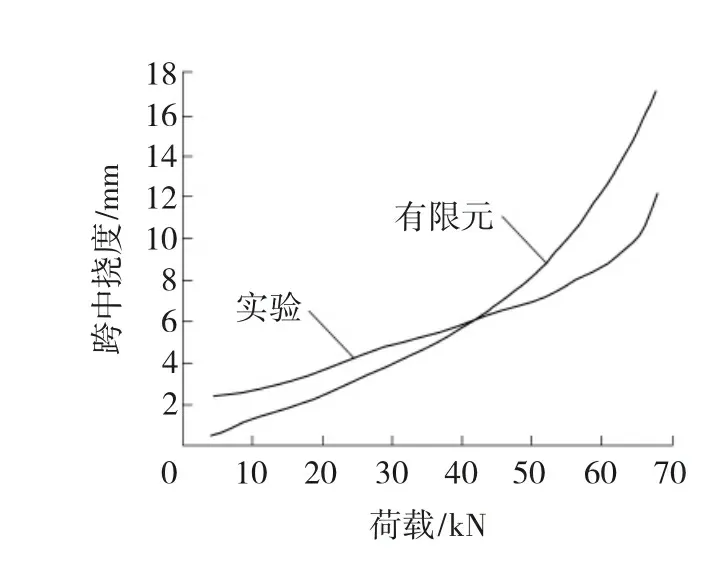
图4　荷载-跨中挠度曲线

由《钢结构设计规范》附录A《结构或构件的变形允许值》可知,蜂窝梁的允许挠度[v]=l/250=10.312 mm,临界荷载取该挠度时对应的荷载计算。由实验所得,当荷载为65.4 kN时,跨中挠度为10.130 mm;当荷载为67.8 kN时,跨中挠度为12.045 mm；跨中挠度为允许挠度10.312 mm时，荷载值由线性内插方法可求得,此荷载为65.63 kN。用类似的方法,利用ANSYS进行实体建模分析得到的临界荷载为55.58 kN。

蜂窝梁挠度达到允许挠度时,对比蜂窝梁挠度结果与实腹梁理论挠度值,结果如表1所示。

表1　蜂窝梁挠度结果与实腹梁理论挠度值对比

注:蜂窝梁1为实验梁,蜂窝梁2为有限元分析梁。

由表1可知,在同跨度的蜂窝梁达到允许挠度时,当量实腹梁在各个测点的挠度为蜂窝梁挠度的15.19%～21.67%,原型实腹梁在各个测点的挠度为蜂窝梁挠度的48.01%～68.49%。这说明扩张比k=1.65的蜂窝梁孔洞对梁腹板截面的削弱严重,过大的扩张比对蜂窝梁挠度贡献并不明显。此时,要充分利用蜂窝梁由于增加截面高度而增加的平面内刚度,另外,还可以通过设置加劲肋等构造措施,对蜂窝梁进行局部加强,从而减小剪切变形产生的挠度。

蜂窝梁发生屈服后,虽然仍具有承载能力和变形能力,但由于其屈服后的挠曲变形增长过快,所以对于扩张比较大的蜂窝梁,在不设置构造措施的情况下,不建议在工程设计时考虑其后期承载能力和变形能力。

利用ANSYS进行实体建模得到的临界荷载值折算为集中荷载为55.58 kN,小于实验所得的临界荷载的15.31%。蜂窝梁达到允许挠度时,临界荷载、百分表2和百分表4处的挠度均适当小于实验所得。这说明利用ANSYS进行实体建模研究蜂窝梁的挠度是安全的,利用ANSYS实体单元对蜂窝梁进行研究具有一定的指导意义。

4　实验和有限元模拟与规范比较

我国GB 50017—2012《钢结构设计规范》征求意见稿中,当扩张比k>1.5时蜂窝梁挠度计算公式为

v=v1+v2+v3=

(1)

式中:v1、v2、v3——弯曲挠度、剪切挠度和剪力次弯矩产生的桥及墩腰转动;

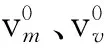
I1——当量实腹梁的毛截面惯性矩;

Ib——桥部空腹截面的惯性矩;

Aw1——当量实腹梁的腹板面积;

AwT——桥部T形截面的腹板面积;

IT——桥部T形截面的惯性矩;

Ip——梁墩的等效惯性矩;

a——桥的跨度；

l1——蜂窝梁的单元长度；

n——蜂窝梁的单元数;

Vi——蜂窝梁第i单元蜂窝孔中点的剪力。

将实验结果及有限元模拟分析结果与式(1)计算结果进行对比。将跨中允许挠度[v]=10.312mm带入式(1),可得临界均布荷载qcr=24.11kN/m。由实验分析得到的蜂窝梁临界均布荷载qcr=25.46kN/m,实验分析结果比式(1)计算结果大5.60%。有限元分析得到的临界均布荷载qcr=21.64kN/m,有限元分析结果比式(1)计算结果小10.24%。上述对比说明，使用式(1)计算蜂窝梁的挠度具有足够的精度。

5　结　论

采用实验和有限元软件ANSYS分析相结合的手段,研究扩张比k=1.65的简支蜂窝梁的挠度特征和挠度计算方法,基于实验与有限元模拟分析及对比结果得到以下结论:

(1)较大的扩张比对蜂窝梁挠度的贡献并不显著,因为开孔对蜂窝梁腹板截面的削弱作用明显,剪切变形产生的挠度较大。

(2)较大扩张比的蜂窝梁在发生屈服后,继续加载时其挠曲变形增长较快,即由弹性阶段进入塑性阶段速度过快,在没有局部加强措施的情况下,不建议在工程设计时考虑其后期承载力和变形能力。

(3)蜂窝梁的破坏形态是局部的屈曲导致结构整体发生失稳破坏。

(4)利用ANSYS的实体单元进行蜂窝梁的研究能较好地反映实际情况,其结果具有一定的指导意义。

(5)当扩张比k>1.5时,使用我国GB50017—2012《钢结构设计规范》征求意见稿中蜂窝梁挠度计算公式(F.0.2-11)计算蜂窝梁的挠度具有足够的精度。

[1]贾连光， 耿琳， 尹晓东. 蜂窝式压弯构件弯矩作用平面内稳定承载力计算的试验验证[J]. 沈阳建筑大学学报， 2009， 25(1)： 61-65.

[2]郑坤龙. 变高度工字截面圆孔蜂窝梁的挠度计算[D]. 长沙： 中南大学, 2007.

[3]何一民. 李鹏鸿, 于力. 蜂窝梁挠度的实用计算方法[J]. 工业建筑, 1994(8): 9-15.

[4]冯春燕, 于大永. 蜂窝梁挠度计算方法研究[J]. 四川建筑科学研究, 2012, 38(1): 65-69.

[5]杨永华, 陈以一. 连续开孔梁的抗弯刚度和挠度的等效计算[J]. 结构工程师, 2006, 22(3): 33-35.

[6]李鹏飞, 姚谦峰. 蜂窝梁应力和挠度计算方法[J]. 建筑结构, 2011, 42(2): 52-55.

[7]张兴杰. 蜂窝梁挠度的简化计算[J]. 四川建筑, 2012, 32(1): 169-171.

[8]李鹏飞, 王新敏, 袁泉, 等. 基于等效面积法的蜂窝梁挠度计算方法研究[J]. 石家庄铁道大学学报： 自然科学版, 2011, 24(3): 8-11.

[9]中冶京诚工程技术有限公司. 《钢结构设计规范》征求意见稿[EB/OL]. (2012-06-30)[2013-08-25]. http://www.gb50017.com/showtopic5443.aspx.

[10]苏益声. 蜂窝钢梁应用研究[D]. 南宁: 广西大学, 2004.

[11]郑懿, 杨俊杰, 王森军, 等. 蜂窝梁的挠度影响因素分析[J]. 浙江工业大学学报, 2007, 35(6): 695-698.

[12]张春玉, 朱柏杰, 乔牧, 等. 六边形孔蜂窝梁抗弯承载力的数值模拟与分析[J]. 黑龙江科技学院学报, 2013, 23(6): 577-580.

[13]姜新佩， 王小燕， 刘丽娜. 预应力碳纤维加固RC梁挠度和裂缝计算[J]. 河北工程大学学报： 自然科学版， 2008(4)： 10-13.

(编辑徐岩)

Experiment and finite-element analysis of deflection of hexagon-hole castellated beams

ZHANGChunyu,SHENYan,ZHAOYanlin,SONGHaitong

(School of Civil Engineering, Heilongjiang University of Science & Technology, Harbin 150022, China)

This paper is concerned specifically with the efforts to delve into the deflection characteristics of castellated beam and its calculation method. The efforts consists of designing the hexagon-hole castellated beams with expansion ratiok=1.65， exploring the deflection changes of simply supported castellated beams subjected to uniform load using experimental and finite element program ANSYS, uncovering the law underlying the deflection change of castellated beams and its damage characteristics, and comparing the deflection formula given in experiment, finite element simulation, and Chinese code for design of steel structure in Chinese draft, as well as critical loads produced by the three. The study reveals the difference in the range of about 5%～10% between the results derived from experiment and finite element simulation and those from the standard formula calculation, suggesting that the standard formula offers enough accuracy. The ANSYS solid modeling method shows promise for the study of castellated beams.

castellated beams; deflection; experiment; finite element analysis

2014-04-22

黑龙江省教育厅科学技术研究项目(12521476)

张春玉(1971-),男,内蒙古自治区阿荣旗人,教授,博士,研究方向:建筑结构设计理论与测试技术,E-mail:hljkjxyzcy@163.com。

10.3969/j.issn.2095-7262.2014.03.019

TU391

2095-7262(2014)03-0312-05

A