围护墙多功能减震结构的地震反应频响分析

朱晓霞，何明胜，石磊巍，郑军伟

（1石河子大学水利建筑工程学院，石河子 832000；2独山子工程建设管理局833600）

为改善调频质量阻尼器（TMD）的鲁棒性，Clark[1]在1988年提出了具有分布频率的多重调谐质量阻尼器（MTMD），此后LgusaT等[2]对此进行了详细的研究，并获得了MTMD系统的摄动解。大量试验和数值分析表明[3-7]，MTMD 的频率范围、阻尼系数和TMD个数是主要影响参数并存在最优问题，只有合理选择MTMD的特征参数，经过合理设计的MTMD系统，才能够有效地减小结构的水平地震反应。分析地震响应一般有时程分析法和频谱分析法，当不同强度的地震波作用时，结构的频率会有很大变化，为了更加全面的分析所测得振动信号，地震反应需要进行频域分析。涂文戈等[8-12]从理论和数值研究对MTMD的频率、模态、振型、频带宽度及场地条件等影响因素进行了研究，指出MTMD适用于高耸和高层结构，地震波的类型、多模态控制、高阶振型及场地条件都对对其地震激励的频谱特性有很大的影响,从而对减震效果也有一定程度的影响。

新型MTMD围护墙多功能减震结构是将普通围护墙与主体结构分离开来,作为TMD子结构墙，并通过脆性抗压件和抗剪件及U型金属阻尼器连接底部设置隔震支座，这种结构的特点是不用另设质量块，且有多种减震功能，做到设置多道防线。我们将脆性抗压件的有效厚度和混凝土强度作为主要影响因素，研究了脆性抗压件的承载力计算方法[13]，通过调整减震结构布置方案，运用SAP2000进行了结构地震反应线性时程分析得出此减震方案具有较好的减震性能[14]。

本文主要研究围护墙多功能减震结构体系的低阶振型模态的地震反应。从理论和试验上验证该体系在频域角度对于减小地震响应的有效性和优越性，并得出其基本参数的影响规律。

1 新型MTMD围护墙多功能减震结构的动力方程

以围护墙TMD为研究对象，地震作用下的结构振动方程：

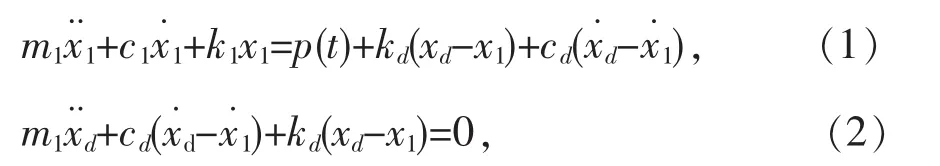
写成矩阵形式

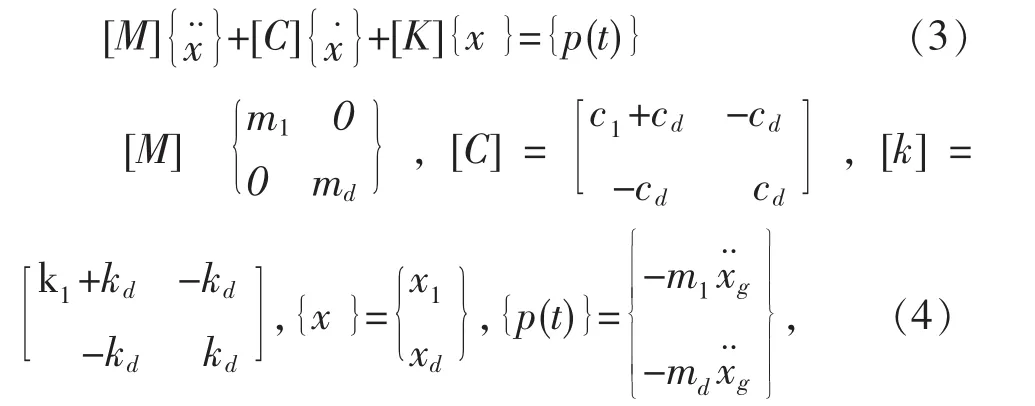
将结构的振动方程（3）进行傅里叶变换得

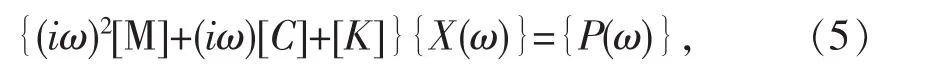
由傅里叶变换后的方程（4）可得

则主框架结构和围护墙结构的传递函数为：

根据随机振动分析，假定基底地震为白噪声，其频谱密度为S0,若忽略主结构阻尼，则主框架结构位移频谱密度及方差分别为：

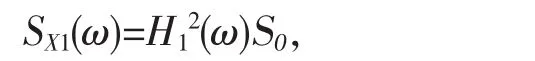
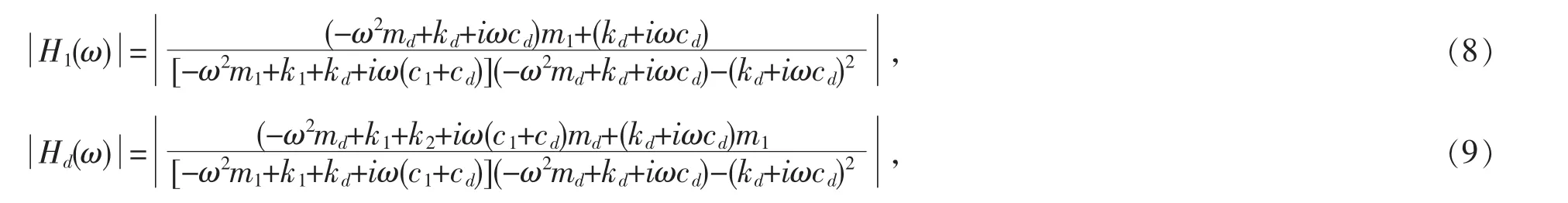
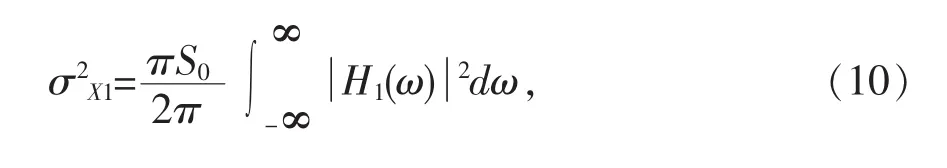
主框架结构与围护墙相对位移δd=x1-xd，其方差为

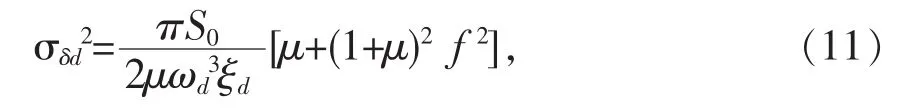
求主结构位移方差最小值，可对式（10）进行求导后可得子结构最优频率比和最优阻尼比为：

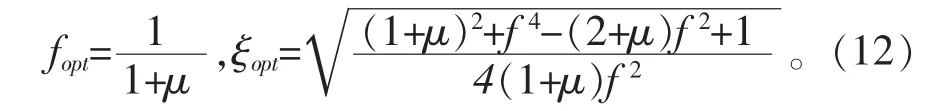
式（12）中：ω1为主结构固有频率；ωd为子结构固有频率；μ为子结构与主结构的质量比；f为子结构与主结构的固有频率比。

由式（12）可知：随着质量比的增大，围护墙的最优频率比逐渐减小；随着频率比的减小，最优阻尼比逐渐增大。

由上述各式可得子结构对新型MTMD围护墙多功能减震结构体系的振动特性（频率、振型、频域传递函数等)的控制效果。当增大子结构的阻尼比，能够减小主结构与子结构相对位移方差，但当阻尼比达到一定数值时，减震效果趋于稳定;当增大TMD个数时，受控结构的频带宽度增大，鲁棒性变好;当质量比增大时，子结构的反向控制力增大，减震效果变好;当频率比减小，共振响应减小，减震效果变好。

2 振动台试验

2.1 结构模型设计

结构模型 （图1）采用A3钢材的钢框架结构，3层单跨钢框架，几何尺寸比例为1∶3，平面尺寸为1.67 m×1.78 m，层高为1 m，总高为3 m，构件均采用各种型钢焊接而成。

楼板质量以C20混凝土配重质量模拟，围护墙为 120 砖墙。 构件截面框架柱：HW100×100×6×8，框架梁：HW150×75×5×7。 框架质量 830 kg，每层楼板质量为680 kg，3层共2040 kg，每片围护墙质量为170 kg。

根据文献[15-17]本试验选择每层2个TMD质量相等的模型。因此仅3层设置TMD，质量比μ约为0.11；2层设置TMD质量比μ约为0.19。TMD刚度主要由U型带片提供，采用2种尺寸（b×t）的阻尼器即 75 mm×3 mm、75 mm×5 mm，2种阻尼器分别为TMD提供的刚度约为：59.5 kN/m，165.2 kN/m，材料为普通A3碳素钢。

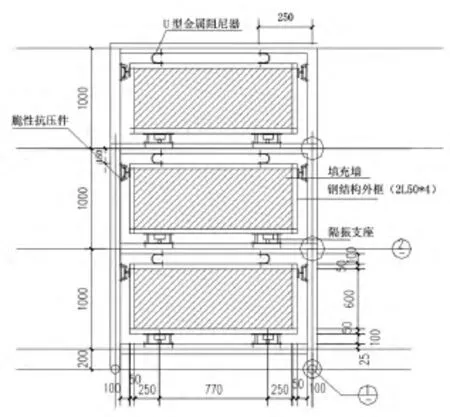
图1 结构模型示意图Fig.1 The schematic diagram of the structure model

模型的相似关系和振动台的主要性能参数见表1和表2。

表1 模型与原型的物理量相似关系Tab.1 Similarity relation of the physical quantities between model and the prototype

表2 振动台的主要性能参数Tab.2 Main performance parameters of shake table

2.2 量测系统急测点确定

2.2.1试验用地震波的确定

采用世界著名的EL-centro波，试验测试沿X跨方向平动,试验根据时间相似常数，将原始地震波沿时间轴压缩为原波的1/3，即10 s。

2.2.2量测系统

试验时模型通过底座牢固安放在模拟地震振动台上。

采用日本鹭宫制作所生产的伺液压式振动台，通过计算机加载控制，采用数字模拟和数字补偿技术使模型得到最佳的地震输入波形。

模型的地震响应用压电加速度传感器、磁致伸缩位移传感器进行量测，并采用INV306D智能信号数据采集分析系统进行数据的采集和分析。

2.3 试验的工况及试验顺序的确定

具体见表3。

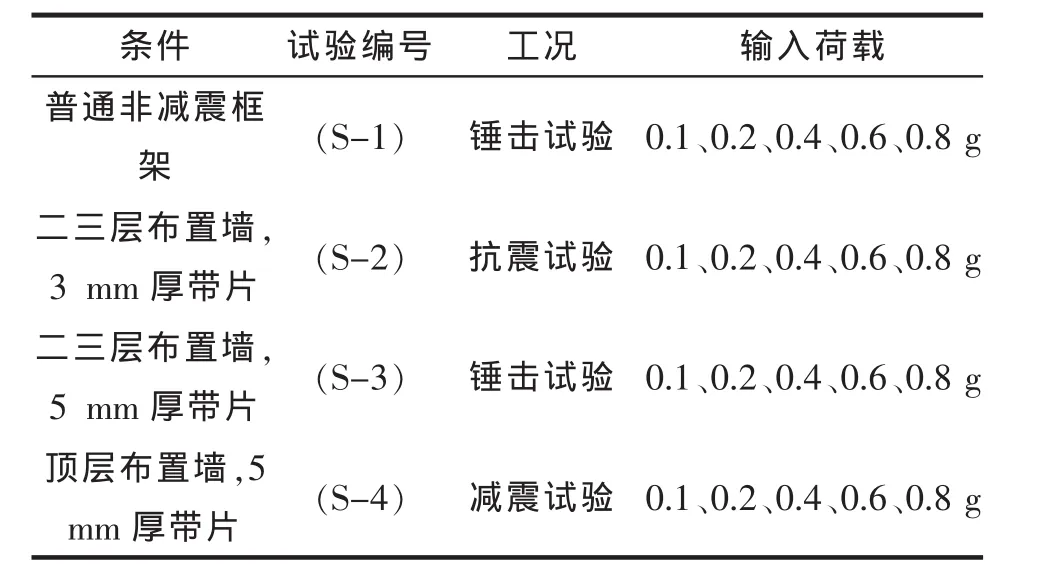
表3 试验工况及顺序Tab.3 Test conditions and order

3 MTMD围护墙多功能减震结构的频响分析

当主框架层数不多时，第一频率对应的响应是主要成分，所以设置子结构围护墙的主要目的是削减第一频率产生的响应。当主框架层数较多时，高阶振型对响应有较大的影响，因此需要设置多个围护墙子结构，可将不同位置的子结构墙调谐到结构不同的频率，得到综合减震的效果。本试验框架只有3层，且当地震作用时，顶层的位移和加速度响应均最大，因此仅对顶层的加速度（位移）响应功率谱密度和频率响应幅值做低阶振型的动力特性分析。

模拟地震波的强度从小到大分别为0.1、0.2、0.4、0.6、0.8 g，选取 0.1、0.4、 0.8 g 作为小震、中震、大震的代表值进行TMD调频减震的频响特性分析。经计算各种减震工况的设置参数：

质量比：μS-2=0.19，μS-3=0.19，μS-4=0.11；

频率比：fS-2=0.574，fS-3=0.301，fS-4=0.585；

最优频率比：fopt（S-2）=0.840，fopt（S-3）=0.840，fopt（S-4）=0.901；

最优阻尼比：ξopt（S-2）=0.524，ξopt（S-3）=0.912，ξopt（S-4）=0.509。

由理论计算得：μ越大，fopt越小，ξ越大，则减震效果越好，可知，减震S-3的减震效果最好。

激励频率与受控频率之比为η=P/ω1，经计算得：η1=0.78， η2=1.388。

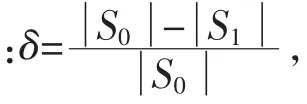
3.1 模型顶层加速度频响分析

图2至5给出了不同强度地震波作用下模型顶层的加速度频响幅值。

由图2至5的响应谱密度和频响幅值在频域的分布特点来看：对于新型MTMD围护墙多功能减震结构，当选择了合适的参数后（这里最主要的参数阻尼比和TMD个数),可以使主框架的响应大幅度的减小，从而达到消能减震的目的。经对比减震结构主框架的功率谱密度明显优于非减震结构，减震结构与非减震结构主频率响应峰值的位置不变，且在主频率处，减震结构的谱密度峰值和频响峰值迅速减小，优化后的控制效果得到增强。峰值对应的响应主频率为 16.55 Hz，η=1.208，η1＜η＜η2， 说明当结构的固有频率ω1较小（η较大时)，子结构能够更好地发挥调谐减震功能，反之，可能会因为框架结构的刚度过大，而使减震效果变差[18]。

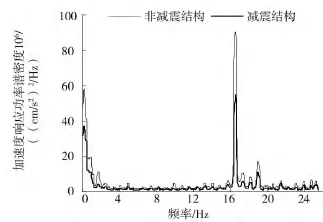
图2 0.4 g El-centro波顶层加速度响应功率谱密度Fig.2 Power spectrum density of acceleration of top layer in 0.4 g EI-centro seismic wave

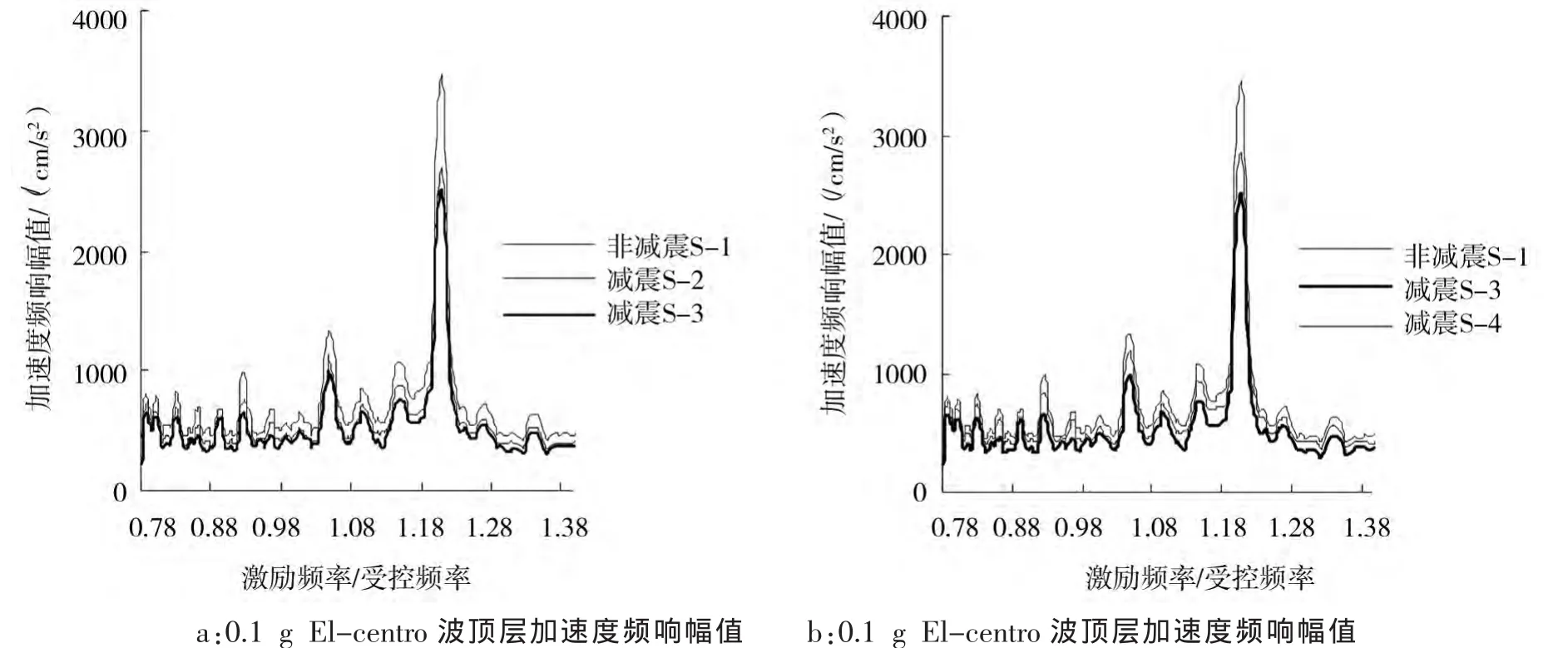
图3 0.1 g alEl-centro波顶层加速度频响幅值Fig.3 Frequency response amplitude of acceleration of top layer in 0.1 g EI-centro seismic wave

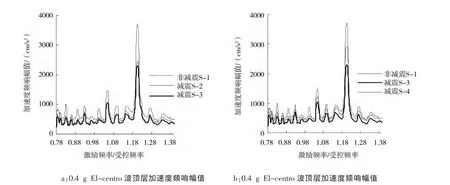
图4 0.4 g alEl-centro波顶层加速度频响幅值Fig.4 Frequency response amplitude of acceleration of top layer in 0.4 gal EI-centro seismic wave

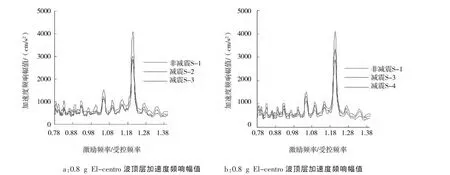
图5 0.8 g El-centro波顶层加速度频响幅值Fig.5 Frequency response amplitude of acceleration of top layer in 0.8 g EI-centro seismic wave

图3至5给出了不同强度地震波作用下模型顶层的加速度频响幅值。图3至图5显示：

（1）当输入地震波加速度为0.1 g时，减震工况S-2、S-3、S-4的峰值降低幅度分别为22.81%、27.41%、17.44%；当输入地震波加速度为0.4 g时，减震工况 S-2、S-3、S-4的峰值降低幅度分别为33.08%、37.72%、21.13%；当输入地震波加速度为0.8 g时，减震工况S-2、S-3、S-4的峰值降低幅度分别为27.17%、29.76%、18.73%。

（2）相比非减震结构，减震结构对于加速度的控制效果都较好，其中以减震工况S-3控制效果最好，在不同强度地震波作用时，以中强度地震波0.4 g的主频响应应峰值降低幅度最大，取得δmax。

对比减震工况S-2和S-3可知，当其它参数不变时，随阻尼比的增大，减震效果越好。对比工况减震S-3与减震S-4可知，阻尼比一定时，TMD个数越多，质量比变大，减震效果越好。减震S-2和减震S-4的减震效果大致相近，但在响应主频率处减震效果相差较大，减震S-2对于加速度响应的控制效果更优，因此，TMD个数对加速度响应控制效果的影响较大。

3.2 模型顶层位移频响分析

图6至9是位移响应功率谱密度和位移频响幅值。

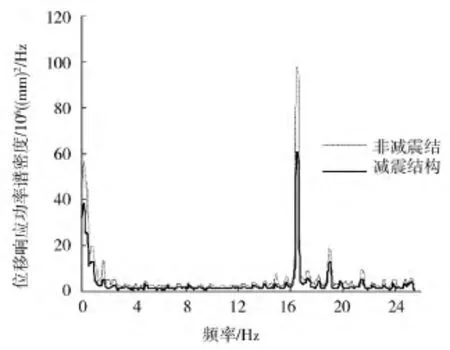
图6 0.4 g El-centro波顶层位移响应功率谱密度Fig.6 Power spectrum density of displacement of top layer in 0.4 g EI-centro seismic wave

从图6至9的位移响应功率谱密度和位移频响幅值可得出和加速度响应分析一致的结论。减震结构主框架的位移功率谱密度更优，在主频率处，减震结构的频响峰值迅速减小。减震结构与非减震结构主频率响应峰值的位置基本不变，位移频响峰值对应的响应主频率为16.5 Hz，η=1.212，与加速度响应的峰值位置基本一致。

由图7至9可知，当输入地震波加速度为0.1 g时，减震工况S-2、S-3、S-4的主频响应峰值处的位移降低幅度分别为19.39%、29.87%、27.86%；当输入地震波加速度为0.4 g时，减震工况S-2、S-3、S-4的峰值降低幅度分别为23.31%、39.97%、36.95%；当输入地震波加速度为0.8 g时，减震工况 S-2、S-3、S-4的峰值降低幅度为 21.37%、35.05%、31.80%。

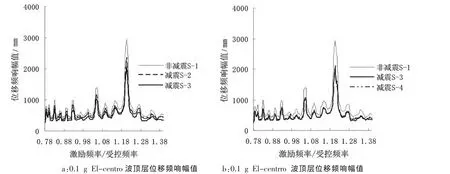
图7 0.1 g El-centro波顶层位移频响幅值Fig.7 Frequency response amplitude of displacement of top layer in 0.1 g EI-centro seismic wave

图8 0.4 g El-centro波顶层位移频响幅值Fig.8 Frequency response amplitude of displacement of top layer in 0.4 g EI-centro seismic wave

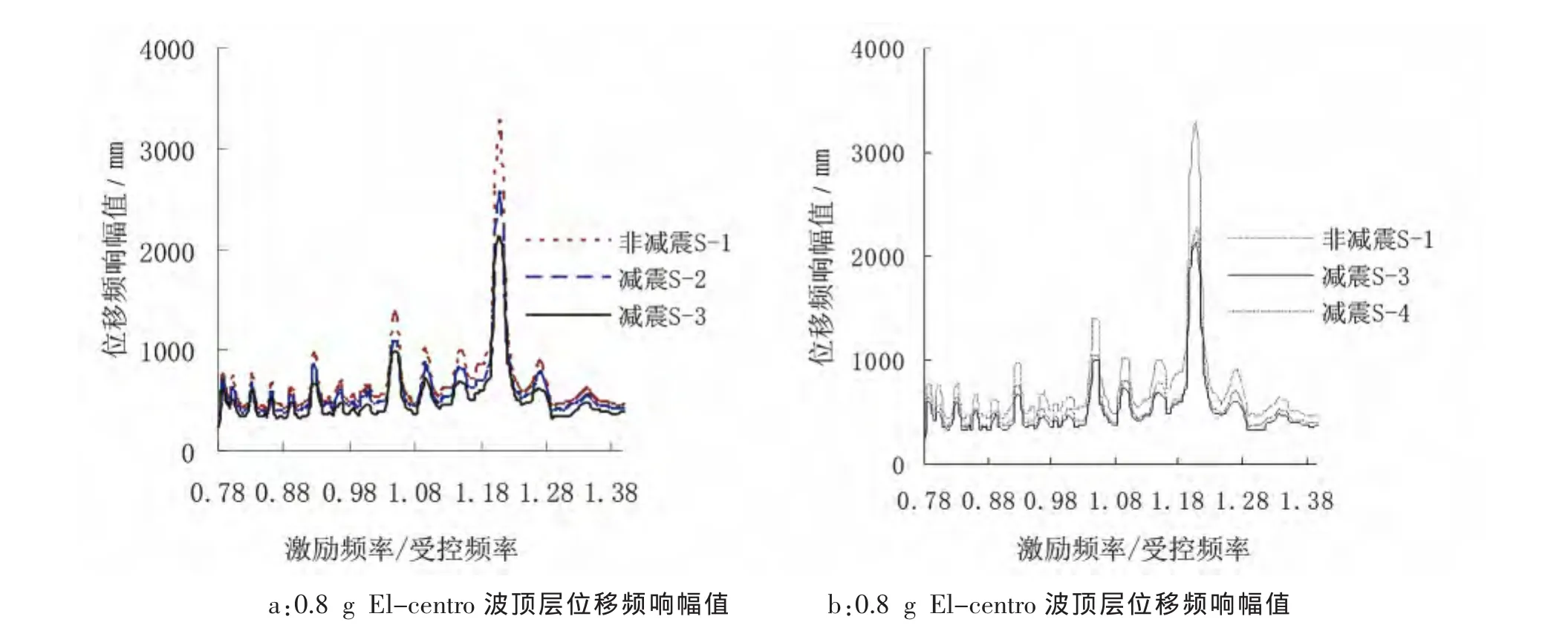
图9 0.8 g El-centro波顶层位移频响幅值Fig.9 Frequency response amplitude of displacement of top layer in 0.8 g EI-centro seismic wave

对比图7至9可知：减震工况S-3的减震效果最优，且在0.4 g时，主频响应峰值的降低幅度最大可达39.97%，取得δmax。减震工况S-4与S-3的减震水平比较相近，其峰值降低幅度可达36.95%，减震工况S-4的减震效果明显优于S-2，说明TMD质量块宜设置在位移向量最大处，阻尼在此减震结构共振区的调谐减震中发挥重要的作用。

对比图3至5和图7至9可知：对于加速度的控制，主频响应峰值处的降低幅度为17.44%～37.71%，而对于位移的控制，主频响应峰值处的降低幅度为19.39%～39.97%，因此减震结构对位移的控制效果略好于对加速度的控制，同时阻尼比对位移控制效果影响较大，而TMD个数对加速度控制效果影响较大。

综上所述，当输入地震波强度较小时，通过脆性抗压件的连接使填充墙能够与主框架一起工作，能够显著提高结构的刚度[19]，控制结构的位移量。随着地震波强度的不断增大，TMD的惯性力增大，对主结构的反作用力也变大，导致脆性抗压件和抗剪件发生破坏，围护墙与主框架分离形成MTMD系统能够发挥调频减震作用。但当地震波强度过大时，这时U型金属带片既有消能作用，又有限位作用，地震作用超过8度设防时，带片进入弹塑性工作状态，此时减震作用是由围护墙子结构的反向惯性力及带片的塑性变形来实现的，减震效果变差。

5 结论

（1）通过建立围护墙多功能减震结构的动力方程以及推导减震结构的频域传递函数和频谱密度可得到各参数在频域方面对此减震结构的减震效果的影响,且主要考虑低阶振型模态的地震反应。

（2）对于加速度和位移的控制，减震结构与非减震结构主频率响应峰值的位置基本不变，且在主频率处，减震结构的谱密度峰值和频响峰值迅速减小，说明优化后的结构控制效果更好，基本达到了削减第一频率响应的目的。

（3）对于加速度的控制，峰值处的减震幅度为17.44%～37.71%；对于位移的控制，峰值处的减震幅度可达19.39%～39.97%。随着输入地震波强度的增大，减震效果先变好后变差，且在400gal时，减震幅度达到最大，符合围护墙多功能减震结构的减震特点及优越性，达到了多种减震功能及设置多道防线的减震目的。

（4）当选择合理参数时，阻尼比对位移反应控制效果影响较大，而TMD个数、质量比对加速度反应控制效果影响较大。从综合的减震效果来看，新型MTMD减震结构对于位移反应的控制更优。

[1]李春祥,熊学玉.用于结构振动控制的MTMD设计模型及最有设计参数[J].四川建筑科学研究,2003,29(3):8-12.

[2]Lgusa T,Xu K.Vibration control using multiple tuned mass dampers[J].Sound and Vibration,1994,175(4):491-503.

[3]蔡国平,孙峰.MTMD控制结构地震反应的特性研究[J].工程力学,2000,17(3):55-59.

[4]李春祥.土木工程结构振动控制的最佳多重调谐质量阻尼器模型[J].四川建筑科学研究,2004,30(1):99-102.

[5]余钱华,胡世德,范立础.桥梁结构MTMD被动控制机理及试验[J].中国公路学报,2008,21(4):50-54.

[6]蔡国平,孙峰.MTMD控制结构地震反应的特性研究[J].工程力学,2000,17(3):55-59.

[7]韩建,金载南,陈景彦,等.多重调频质量阻尼器在控制结构振动中的应用[J].东北电力学院学报,2001,21(4):37-40.

[8]唐柏鉴,李亚明.大跨屋盖结构的竖向MTMD减震控制[J].特种结构,2007,24(1):64-67.

[9]鲁杰,张洵安,秦相军,等.复合MTMD在结构控制中的优化设计[J].广东工业大学学报,2008,25(1):97-100.

[10]涂文戈,邹银生.MTMD对建筑结构多模态控制的减震分析[J].地震工程与工程振动,2003,23(5):174-179.

[11]刘保东,朱晞.MTMD系统抗震控制研究[J].工程力学,2003,20(1):127-130.

[12]叶继红,陈月明,沈世钊.TMD减震系统在网壳结构中的应用[J].哈尔滨建筑大学学报,2000,33(5):10-14.

[13]刘成刚,何明胜,张红彬,等.围护墙多功能减震结构脆性抗压件的承载力计算[J].石河子大学学报:自然科学版,2010,28(2):246-250.

[14]张红彬,何明胜,刘成刚.围护墙多功能减震结构的减震性能[J].石河子大学学报:自然科学版,2009,27(5):637-641.

[15]李春祥.地震作用下基于多准则的最优调谐质量阻尼器[J].上海交通大学学报,2002,36(11):1630-1633.

[16]李春祥.地震作用下高层建筑TMD控制研究与设计[J].上海交通大学学报,1999,33(6):746-749.

[17]李春祥.基于系统参数均匀分布的新型多重调谐质量阻尼器模型[J].上海交通大学学报,2005,39(5):775-781.

[18]张敏.建筑结构抗震分析与减震控制[M].成都:西南交通大学出版社,2007:978-810.

[19]刘玉姝,李国强.带填充墙钢框架结构抗侧力性能试验及理论研究[J].建筑结构学报,2005,26(3):78-84.