Shear velocity criterion for incipient motion of sediment

Francisco J. M. SIMÕES*

U.S. Geological Survey, Geomorphology and Sediment Transport Laboratory, Golden, CO 80403, USA

1 Introduction

The concept of excess shear stress has played a major role in the prediction of sediment transport rates. It is also used in problems involving channel erosion and stable channel design.Underlying this concept is the phenomenon of incipient motion, i.e., the transition from a stationary state to a state of initial (incipient)motion of the sediment particles in response to an increase in the hydrodynamic forces acting on a bed of loose sediment. This hard-to-define critical threshold condition has been approached using diverse physical parameters, such as the shear velocity (U*)and depth-mean velocity (U), but none has proven as popular as the traditional Shields (1936)curve based on the threshold shear stress.

Shields (1936)expressed the critical shear stress for the initiation of motion as a relation between the nondimensional shear stress θ (also called the Shields parameter or the Shields entrainment function)and the grain Reynolds number based on the shear velocity, R*,defined as

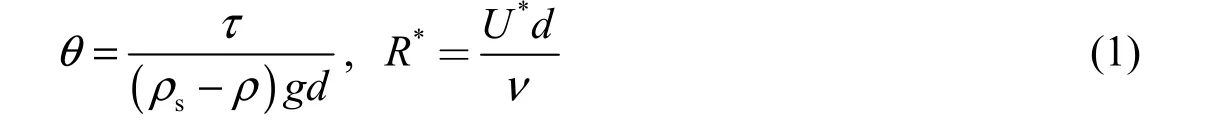
where s is the specific gravity of the sediment, and s=ρsρ. The use of d*eliminates the simultaneous use of U*in the abscissa and the ordinate of the Shields diagram, reducing data scatter and eliminating the need for an iterative process to find θcfor a particular set of hydraulic and sediment conditions.

Substantially more data has been collected subsequent to Shields’ work, significantly expanding the range of experimental conditions. One of the issues that became significant with the arrival of these new experimental sets was the scatter of the data. This scatter is apparent in Fig. 1, where the empirical threshold curves of Paphitis (2001)are plotted against measurement data. Some authors, such as Zanke (2003)and Vollmer and Kleinhans (2007), attempted to explain and predict the disperse nature of the data. However, their analyses are complex and depend on variables that are unknown in most practical applications. Others suggest the use of different dependent variables that are better able to collapse the data into narrower bands, and consequently, are more amenable to conversion to analytic expressions.

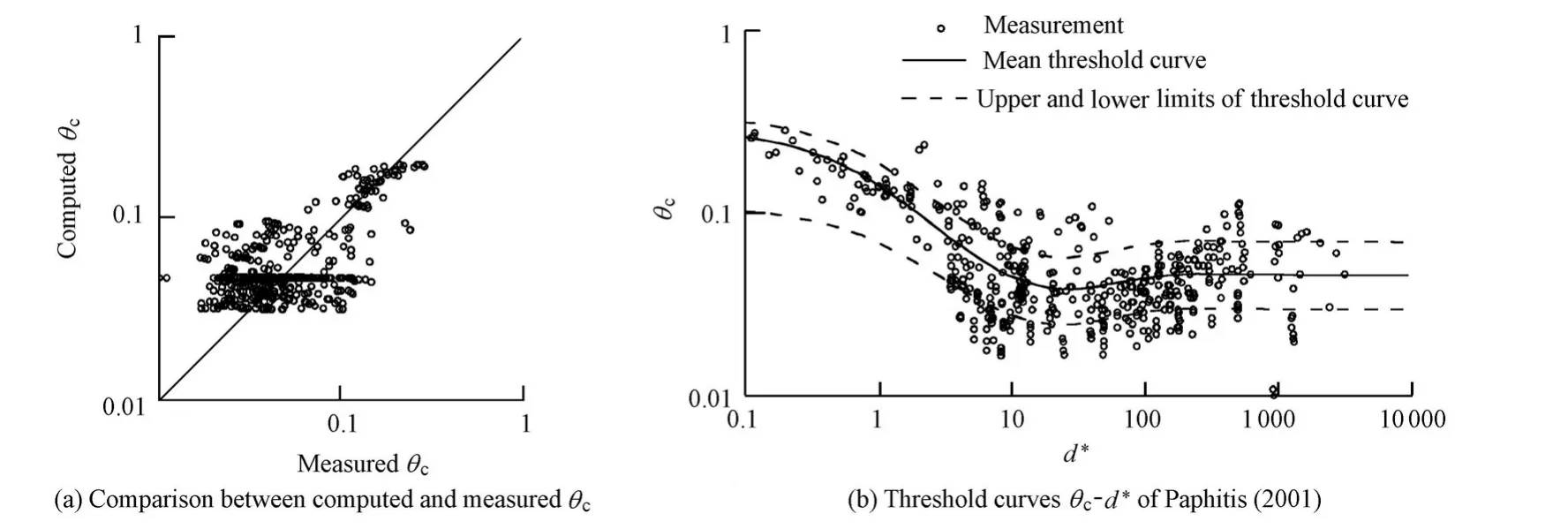
Fig. 1 Shields diagram for incipient motion of Paphitis (2001)and its comparison with measurements

Liu (1958)proposed the use of the movability number of the sediment particle, defined as Λ= U*w , where w is the settling velocity of the individual sediment particle, as an alternative to the Shields parameter, and developed a Λc-R*relation, where Λcis the movability number

2 Previous analyses

While searching for a criterion for the initiation of ripple formation, Liu (1957, 1958)proposed the movability number Λ of the sediment particle. The relation between Λ and θ can be easily shown for spherical particles. For spherical grains,

where Cdis the drag coefficient. With Eq. (3), we can obtain

According to the definition of θ, the relation between Λ and θ can be obtained:

This implies that if θchas a universal curve as a function of R*(or d*), Λ must be Λcfor incipient motion conditions. Furthermore, the fact that Λ is proportional to the square root of θ naturally results in a reduction of data scatter around the curve for Λc.

The movability number has been shown to be an effective alternative to the Shields parameter. Liu (1958)was the first to recast the original Shields diagram into a Λc- R*curve that resulted in narrower bands of data scatter. Collins and Rigler (1982)argued that any method for estimating the threshold of motion should incorporate information about the particle shape and specific gravity, and recommended the particle’s settling velocity as a means to accomplish that. Komar and Clemens (1986)showed that the computation of w for sediment grains is at least as accurate as the determination of the threshold of motion, which relies on a somewhat subjective measurement, and developed a mechanical model of grain pivoting relating the threshold of motion to Λ. They also proposed Λc- R*and Λc- Ξ curves,but a limited amount of data were used, therefore limiting the range of application of their results.

Paphitis (2001)analyzed different types of empirical threshold curves and showed that the use of Λ offers a clear advantage over the use of the Shields parameter and the critical shear velocity. Using the most extensive dataset, he derived a new relation for Λcas a function of the grain Reynolds number:

Using this type of threshold curve, motion is determined to take place when the hydraulic and sediment conditions are such that Λ＞ Λc; otherwise, there is no sediment motion. Eq. (6), which is Eq. (20)of Paphitis (2001), is valid in the range of 0.1 ＜R*＜105, and it is shown in Fig. 2 along with experimental data. Fig. 2(b)shows an improved collapse of the measurements along the analytic curve when compared to the θ-based curve of Fig. 1(b)(the same experimental dataset is used in Figs. 1 and 2). There is, however, still a significant deviation between the experimental data and Eq. (6), especially in the lower range of R*. This may be attributed to the more limited range of data used by Paphitis (2001)in the derivation of Eq. (6),which was limited to the range of R*＞0.1. Another limitation of Eq. (6)resides in the use of R*as the independent variable, whereby U*is present in both Λ and R*.

Fig. 2 Threshold for incipient motion of Paphitis (2001)and its comparison with measurements

Beheshti and Ataie-Ashtiani (2008), who also found Λ to be a more suitable parameter for determining the threshold of motion, tried to eliminate the latter limitation by deriving the following Λc- d*curve:

This equation, which is valid in the approximate range of 0.4 ＜ d*＜ 1000, is shown in Fig. 3.As can be seen from Fig. 3, agreement between measurements and predictions is fair, but this equation shows the wrong behavior for large values of d*(d*＞500)and overpredicts Λcin the lower range of d*.

Fig. 3 Threshold for incipient motion of Beheshti and Ataie-Ashtiani (2008)and comparison with measurements

3 Derivation of new incipient motion equation

The work presented herein is based on experimental data collected independently by many researchers. There are important considerations concerning the definition of the sediment threshold that result in subjectivity and consequential uncertainty associated with such data. It is beyond the scope of the present work to dwell on these issues and the reader is referred to section 6 of Paphitis (2001)for more detailed comments.

In this study, 517 sets of data obtained from many different sources and distinct physical settings were used. The origin of the data and their main characteristics are presented in Table 1, which includes the data used in the original work of Shields (1936)and plotted in Figs. 1 through 3. Not all the data presented in the original sources were used: the sets that did not contain enough information for an accurate calculation of the particle’s settling velocity were discarded. Nonetheless, the sediments associated with the data sets in Table 1, made of natural and artificial grains, offer a variety in shape and density and a sufficient number for statistical significance. Bed configurations also varied from grains of almost a uniform size to mixtures with relatively large sorting coefficients. Most data were collected in controlled laboratory settings, but some were collected in the field. The criterion used for the definition of incipient motion was also varied: visual inspection (a few or all particles moving),extrapolation methods, and stochastic approaches. The reader is referred to the original publications for further details.

Settling velocities were calculated using the procedure given by Dietrich (1982). This method requires knowledge of water temperature, the sediment particles’ shape (the Corey shape factor and Powers’ roundness factor P), and their nominal diameter dN(the diameter of a sphere with the same volume as the particle). The shape parameters had to be estimated (e.g.,P = 6 for spheres and well rounded particles, P = 3.5 for natural sediments, and P = 2 for crushed sediments), and data without enough information for an adequate estimate were discarded. Similarly, when sediment mixtures were used, some authors provided information about the nominal diameter of the mixture, and others did not. In the latter case, a nominal diameter dN=d500.9 was used (d50is the sieve size through which 50% of the sediment passes). Note, however, that d50was always used for calculating d*.

Table 1 Sources of data used in this study

The data in Table 1 were randomly divided into two approximately equal groups in the following manner: the data sets were sorted by their sizes and numbered accordingly (the data set of Collins and Riegler (1982)was assigned number 1, the data set of Pilotti and Menduni(2001)was assigned number 2, etc.), and the data sets with odd numbering were assigned to group 1, while the data sets with even numbering were assigned to group 2. Group 1 is used in this section and group 2 is set aside for validating the new derivation, which is done in the next section.

A nonlinear least-squares procedure was used to accomplish the fit of a curve to the data.The final expression found is

Fig. 4 Derived threshold for incipient motion Eq. (8)and its comparison with measurements

4 Validation of proposed equation

The results shown in Fig. 4 present the goodness-of-fit of the derived curve to the data.However, Eq. (8)represents an empirical fit, and its validity is limited to the specific hydraulic conditions and particle characteristics associated with the data sets used for its derivation.Therefore, this analytic formula must be treated with caution. To determine its predictive ability, it must be validated using data sets that are independent from those used for its derivation. Here, data group 2 is used for that purpose.

Table 2 Statistical goodness-of-fit parameters for different curves

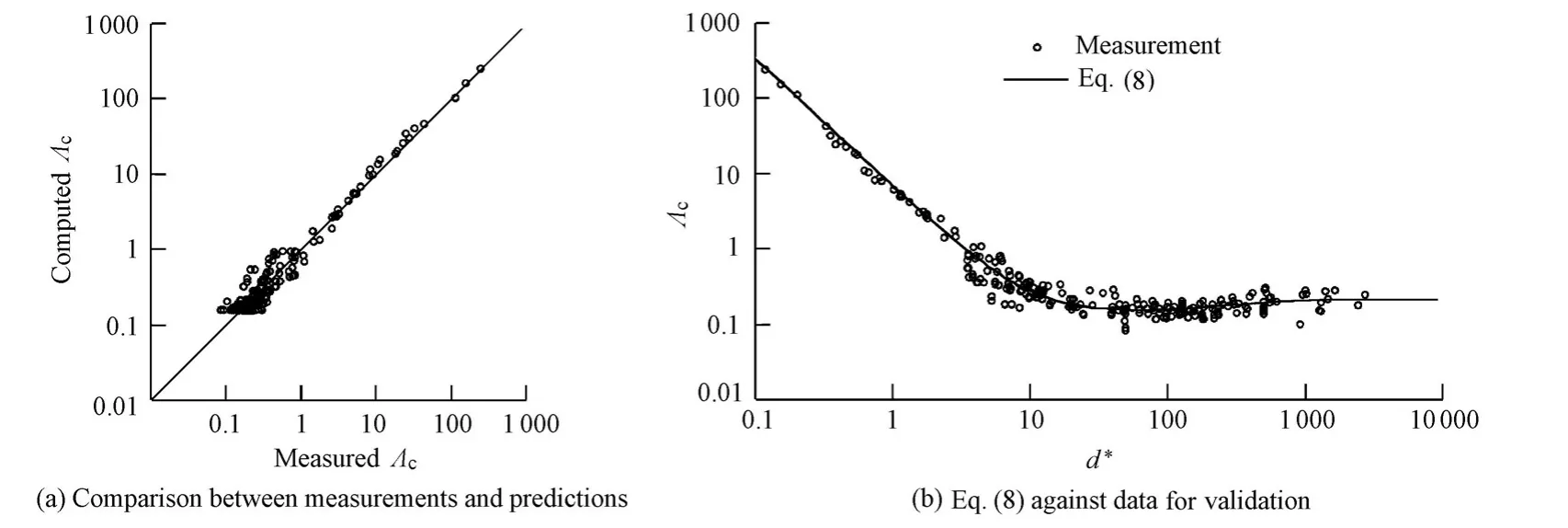
Fig. 5 Validation of Eq. (8)using independent data

It is apparent that the proposed equation provides a statistically significant improvement over the equation of Beheshti and Ataie-Ashtiani (2008), as demonstrated by the respective values of the mean discrepancy ratio and the mean normalized error in Table 2. Additionally,the value of the standard deviation also reflects a larger amount of data scatter present in Beheshti and Ataie-Ashtiani’s (2008)equation. This scatter is also easily discovered by comparing the plots in Fig. 3 with those in Fig. 5.

5 Conclusions

In spite of significant data scatter, empirical threshold-of-motion curves based on the Shields parameter are commonly used in sediment transport theories. Several researchers addressed the issue by replacement of the Shields parameter θ with the movability number Λ.The use of Λ over θ offers several advantages: it incorporates particle shape information and specific density via the use of the settling velocity w; Λ is proportional to θ1/2, therefore reducing data scatter; and Λ is related to turbulence (i.e., to upward and downward turbulent fluctuations), therefore naturally incorporating its effects in the initiation of the motion of sediment particles.

It is necessary to compute the settling velocity for some of the irregularly shaped sediment particles used in this study. The computation of w was done using Dietrich’s (1982)method due to its flexibility in incorporating particle shape and roundness. There are other simpler methods of calculating the sediment particle settling velocity. However, they have smaller ranges of applicability.

This investigation corroborated the view that using Λ does improve the collapse of measured data into a line that is very well defined in a Λc- d*diagram. An empirical expression, Eq. (8), was derived by data fitting. Statistical parameters show a high degree of agreement between the analytic expression and experimental data. We therefore established that this new equation can be used effectively for the computation of the threshold of incipient sediment motion, providing a simple and practical calculation procedure that is more accurate than those based on the traditional Shields parameter.

Ashworth, P. J., Ferguson, R. I., Ashmore, P. E., Paola, C., Powell, D. M., and Prestegaard, K. L. 1992.Measurements in a braided river chute and lobe, 2: Sorting of bed load during entrainment, transport, and deposition. Water Resoures Research, 28(7), 1887-1896. [doi:10.1029/92WR00702]

Bathurst, J. C., Graf, W. H. and Cao, H. H. 1987. Bed load discharge equations for steep mountain rivers.Thorne, C. R., et al. eds., Sediment Transport in Gravelbed Rivers, 453-491. New York: John Wiley & Sons.

Beheshti, A. A., and Ataie-Ashtiani, B. 2008. Analysis of threshold and incipient conditions for sediment movement. Coastal Engineering, 55(5), 423-430. [doi:10.1016/j.coastaleng.2008.01.003]

Carling, P. A. 1983. Threshold of coarse sediment transport in broad and narrow natural streams. Earth Surface Processes and Landforms, 8(1), 1-18. [doi:10.1002/esp.3290080102]

Casey, H. J. 1935a. About Bedload Movement. Ph. D. Dissertation. Berlin: Technischen Hochschule.(In German)

Casey, H. J. 1935b. About Bedload Movement. Berlin: Communications of the Prussian Laboratory of Hydraulics and shipbuilding. (In German)

Collins, M. B., and Rigler, J. K. 1982. The use of settling velocity in defining the initiation of motion of heavy mineral grains, under unidirectional flow. Sedimentology, 29(3), 419-426.

Dey, S., and Debnath, K. 2000. Influence of streamwise bed slope on sediment threshold under stream flow.Journal of Irrigation and Drainage Engngineering, 126(4), 255-263. [doi:10.1061/(ASCE)0733-9437(2000)126:4(255)]

Dey, S., and Raju, U. V. 2002. Incipient motion of gravel and coal beds. Sadhana-Academy Proceedings in Engineering Sciences, 27(5), 559-568.

Dietrich, W. E. 1982. Settling velocity of natural particles. Water Resources Research, 18(6), 1615-1626.[doi:10.1029/WR018i006p01615]

Everts, C. H. 1973. Particle overpassing on flat granular boundaries. Journal of the Waterways, Harbors and Coastal Engineering Division, 99(4), 425-438.

Ferguson, R. I., Prestegaard, K. L., and Ashworth, P. J. 1989. Influence of sand on hydraulics and gravel transport in a braided gravel bed river. Water Resources Research, 25(4), 635-643. [doi:10.1029/WR025i004p00635]

Ferguson, R. I. 1994. Critical discharge for entrainment of poorly sorted gravel. Earth Surface Processes and Landforms, 19(2), 179-186. [doi:10.1002/esp.3290190208]

Gilbert, G. K. 1914. The Transportation of Debris by Running Water. Washington: U.S. Government Printing Office.

Grass, A. J. 1970. Initial instability of fine bed sand. Journal of the Hydraulics Division, 96(3), 619-632.

Hammond, F., Heathershaw, A., and Langhorne, D. 1984. A comparison between Shields’ threshold criterion and the movement of loosely packed gravel in a tidal channel. Sedimentology, 31(1), 51-62.

Komar, P. D., and Clemens, K. E. 1986. The relationship between a grain’s settling velocity and threshold of motion under unidirectional currents. Journal of Sedimentary Research, 56(2), 258-266.

Komar, P. D., and Carling, P. A. 1991. Grain sorting in gravel-bed streams and the choice of particle sizes for flow-competence evaluations. Sedimentology, 38(3), 489-502.

Kramer, H. 1932. Modellgeschiebe und schleppkraft. Ph. D. Dissertation. Dresden: Technischen Hochschule.(In German)

Kramer, H. 1935. Sand mixtures and sand movement in fluvial models. Transactions of the American Society of Civil Engineers, 100(1), 798-878.

Liu, T. Y. 1935. Transportation of the Bottom Load in an Open Channel. M. S. Dissertation. Iowa: University of Iowa.

Liu, H. K. 1957. Mechanics of sediment ripple formation. Journal of the Hydraulics Division, 83(2), 1-23.

Liu, H. K. 1958. Closure: Mechanics of sediment ripple formation. Journal of the Hydraulics Division, 84(5),5-31.

Luque, R. F., and van Beek, R. 1976. Erosion and transport of bed-load sediment. Journal of Hydraulic Research, 14(2), 127-143.

Mantz, P. A. 1975. Low Transport Stages by Water Streams of Fine, Cohesionless Granular and Flaky Sediments. Ph. D. Dissertation. London: University of London.

Meyer-Peter, E., and Müller, R. 1948. Formulas for bed-load transport. Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, 39-64. Delft: IAHR.

Milhous, R. T. 1973. Sediment Transport in a Gravel-bottomed Stream. Ph. D. Dissertation. Corvallis: Oregon State University.

Misri, R. L., Garde, R. J., and Ranga Raju, K.G. 1984. Bed load transport of coarse nonuniform sediment.Journal of Hydraulic Engineering, 110(3), 312-328.

Mizuyama, T. 1977. Bedload Transport in Steep Channels. Ph. D. Dissertation. Kyoto: Kyoto University.

Neill, C. R. 1967. Mean-velocity criterion for scour of coarse uniform bedmaterial. Proceedings of the 12th Congress of the International Association of Hydraulics Research, vol. 3, 46-54. Delft: IAHR.

Paphitis, D. 2001. Sediment movement under unidirectional flows: an assessment of empirical threshold curves. Coastal Engineering, 43(3-4), 227-245. [doi:10.1016/S0378-3839(01)00015-1]

Petit, F. 1994. Dimensionless critical shear stress evaluation from flume experiments using different gravel beds. Earth Surface Processes and Landforms, 19(6), 565-576. [doi:10.1002/esp.3290190608]

Pilotti, M., and Menduni, G. 2001. Beginning of sediment transport of incoherent grains in shallow shear flows. Journal of Hydraulic Research, 39(2), 115-124.

Powell, D. M., and Ashworth, P. J. 1995. Spatial pattern of flow competence and bed load transport in a divided gravel bed river. Water Resources Research, 31(3), 741-752. [doi:10.1029/94WR02273]

Rao, A. R., and Sitaram, N. 1999. Stability and mobility of sand-bed channels affected by seepage. Journal of Irrigation and Drainage Engineering, 125(16), 370-379. [doi:10.1061/(ASCE)0733-9437(1999)125:6(370)]

Shields, A. 1936. Application of Similarity Principles and Turbulence Research to Bedload Movement. Berlin:Wasserbau Schiffbau. (English translation by Ott, W. P., and van Uchelen, J. C., Hydraulics Laboratory,California Institute of Technology)

Talapatra, S. C., and Ghosh, S. N. 1983. Incipient motion criteria for flow over a mobile bed sill. Proceedings of the 2nd International Symposium on River Sedimentation, 459-471. Nanjing: Water Resources and Electric Power Press.

U.S. Waterways Experiment Station (USWES). 1935. Study of River Bed Material and Their Movement: With Special Reference to the Lower Mississippi River. Vicksburg: U.S. Waterways Experiment Station.

Vollmer, S., and Kleinhans, M. G. 2007. Predicting incipient motion, including the effect of turbulent pressure fluctuations in the bed. Water Resources Research, 43(5), W05410. [doi:10.1029/2006WR004919]

Ward, B. D. 1968. Surface Shear at Incipient Motion of Uniform Sands. Ph. D. Dissertation. Tucson:University of Arizona.

Wathen, S. J., Ferguson, R. I., Hoey, T. B., and Werritty, H. A. 1995. Unequal mobility of gravel and sand in weakly bimodal river sediments. Water Resources Research, 31(8), 2087-2096. [doi:10.1029/95WR01229]

White, S. J. 1970. Plane bed thresholds of fine grained sediments. Nature, 228, 152-153. [doi:10.1038/228152a0]

Wilcock, P. R. 1987. Bed-load Transport of Mixed-size Sediment. Ph. D. Dissertation. Cambridge:Massachusetts Institute of Technology.

Yalin, M. S. 1972. Mechanics of Sediment Transport. New York: Pergamon Press.

Yalin, M. S., and Karahan, E. 1979. Inception of sediment transport. Journal of the Hydraulics Division,105(11), 1433-1443.

Yalin, M. S., and da Silva, A. M. F. 2001. Fluvial Processes. Delft: International Association of Hydraulic Research.

Zanke, U. C. E. 2003. On the influence of turbulence on the initiation of motion. International Journal of Sediment Research, 18(1), 17-31.