Risk assessment of water security in Haihe River Basin during drought periods based on D-S evidence theory

Qian-jin DONG*, Xia LIU

1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China

2. Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan University, Wuhan 430072, P. R. China

3. School of Geography and Planning, Sun Yat-sen University, Guangzhou 510275, P. R. China

The D-S evidence theory was established by Shafer (1976) and Dempster (1967). In the D-S evidence theory, information is evidence to support the results of a decision and is not 100% reliable. In addition, the same pieces of evidence may have different contributions to eventual decision making because their weights are different; the weights reflect the relative importance of the evidence. Dempster’s combination rule, which is the foundation of the D-S evidence theory, is as follows:

Risk assessment of water security in Haihe River Basin during drought periods based on D-S evidence theory

Qian-jin DONG*1,2, Xia LIU3

1. State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, P. R. China

2. Hubei Provincial Collaborative Innovation Center for Water Resources Security, Wuhan University, Wuhan 430072, P. R. China

3. School of Geography and Planning, Sun Yat-sen University, Guangzhou 510275, P. R. China

The weights of the drought risk index (DRI), which linearly combines the reliability, resiliency, and vulnerability, are difficult to obtain due to complexities in water security during drought periods. Therefore, drought entropy was used to determine the weights of the three critical indices. Conventional simulation results regarding the risk load of water security during drought periods were often regarded as precise. However, neither the simulation process nor the DRI gives any consideration to uncertainties in drought events. Therefore, the Dempster-Shafer (D-S) evidence theory and the evidential reasoning algorithm were introduced, and the DRI values were calculated with consideration of uncertainties of the three indices. The drought entropy and evidential reasoning algorithm were used in a case study of the Haihe River Basin to assess water security risks during drought periods. The results of the new DRI values in two scenarios were compared and analyzed. It is shown that the values of the DRI in the D-S evidence algorithm increase slightly from the original results of Zhang et al. (2005), and the results of risk assessment of water security during drought periods are reasonable according to the situation in the study area. This study can serve as a reference for further practical application and planning in the Haihe River Basin, and other relevant or similar studies.

risk assessment; water security; drought periods; entropy; D-S evidence theory; evidential reasoning algorithm; Haihe River Basin

1 Introduction

Water security takes into account not only the quantity but also the quality of water resources: it is a status in which water characteristics (including chemical and physical characteristics) and relevant water events are innocuous or at least tolerable to human beings. With increasing demand on water resources, floods, water shortage, and water environmental degradation have become serious threats to water security.

As far as water quantity is concerned, a surplus volume of water usually leads to floods,while an extremely small volume of water tends to cause drought. Compared with floods, droughts are insidious, pervasive (Loáiciga 2005), and irregular, and because droughts often cannot be detected in advance, they tend to lead to more enormous losses than flood events. In fact, drought is a recurring and slow-onset disaster associated closely with the shortage of water resources (Zamani et al. 2006).

The main cause of drought is a prolonged absence, deficiency, or poor distribution of precipitation (WMO 1999). During drought periods, the daily water demand cannot be completely satisfied, and the public often reacts strongly and negatively to the occurrence of water shortage (Merabtene et al. 2002). Therefore, risk management of drought is a necessary and dominant consideration for sustainable development of water resources (Jinno et al. 1995; Cancelliere et al. 1998).

The risk management of drought, including risk assessment of drought, which has been applied widely as an effective support of measurement based on extensive consideration of influencing factors, aids scientific decision making, decreasing the losses caused by drought, and minimizing the harmful effects of drought to a large degree (Huang and Chou 2008; Kao and Govindaraju 2010). Although there has been much research on risk management of water resources since the birth of the risk concept in the 1970s (Lowrance 1976; Rowe 1977; Shang and Wang 2013), the literature rarely deals with risk management of water security during drought periods. The results of risk assessment should be one rather important point of consideration for decisions meant to mitigate risks of water security during drought periods.

Despite the fact that there have been some studies of risk assessment of water security during drought periods, analysis of uncertainties of water security during drought periods is often neglected when assessing risks within drought events. Thus, the uncertainties of water security during drought periods should be considered. Otherwise, the real risk cannot be clarified. Furthermore, due to peculiar probabilistic characteristics of drought (Loáiciga and Leipnik 1996; Chung and Salas 2000), it is believed that many uncertainties exist in water security during drought periods. The common results based on simulation models are also uncertain. Thus, the uncertainties of risk assessment for water security during drought periods should be considered because the results of risk assessment influence the decision to mitigate risks to water security, and the risk to water security during drought periods may be underestimated.

Risk assessment of water security during drought periods tends to use the three indices of reliability, resiliency, and vulnerability, as well as the drought risk index (DRI). The DRI is usually a linear weight function based on the three indices (Mondal and Wasimi 2007; Srdjevic and Obradovic 1995), and it was used in this study because of its compact formulation. However, the relationships between the three indices are not clear in practice, and the physical meanings of the weights of the three indices are also ambiguous. Thus, the weights of the threeindices are difficult to determine and the DRI is also not capable of being calculated objectively. Therefore, in order to solve the problem of weights of the three indices, drought entropy based on the Shannon entropy is presented in this paper. The evidential reasoning algorithm based on the Dempster-Shafer (D-S) theory was used to redesign the DRI with consideration of uncertainties in risk assessment of water security during drought periods. The presented approaches for risk assessment of water security during drought periods have not been discussed in other papers. The real risk during drought periods in the Haihe River Basin is demonstrated in this paper.

2 Water security risk assessment based on drought entropy and D-S evidence theory

2.1 Water security risk assessment index system

The risk to water security during drought periods can be defined simply as a probability that a water supply system cannot satisfy water demand. When water demand is larger than water supply, a risk event occurs. As mentioned above, risk analysis of a water resources system always involves reliability, resiliency, and vulnerability (Moy et al. 1986), which are used to build the DRI of a region. Thus, risk assessment of water security during drought periods is used to determine the DRI, and the DRI represents the risk degree for a certain alternative or region. The DRI is a probability index that reflects the degree of loss due to failure events of water supply systems; the larger the DRI value is, the severer the water shortage will be. Generally, the reliability index (Rel) can be described as the overall system performance over time in evaluating the degree of water demand being satisfied by the water supply system, according to Hashimoto et al. (1982a, 1982b). The resiliency (Res) is a statistical characteristic calculated from all failures that occur. The vulnerability index (Vul) is introduced as a measure of risk effect and severity degree in regard to social and economic systems. More details on these indices can be found in Hashimoto et al. (1982a, 1982b). Therefore, the value of the DRI (IDR) can be obtained as follows:

where ω1, ω2, and ω3are the weights of 1−Rel, 1−Res, and Vul, respectively, andis the failure risk of a water supply system; (1 −Res) is the non-recovery risk of the water supply system; and Vuldescribes the degree of water shortage of the water supply system (Jinno et al. 1995). To obtain the value of the DRI,1ω,2ω, and3ω should be known in advance, and they are usually assumed to be equal to one another (Zhang et al. 2005). However, in fact, weights of the indices should be determined according to the importance of each given factor. This leads us to the problem of determining the weights.

2.2 Determination of values of weights

Generally, weights can be assigned subjectively, based on experts’ knowledge or on the statistics (Sun et al. 2008). In terms of water security during drought periods, if drought is considered to be a passive hazard (WMO 1999), the drought entropy can be presented based on the information entropy proposed by Shannon (1948). That is to say, as information entropy is a measure of uncertainties in a system, the drought entropy quantitatively presents information related to the possibility of a drought event occurring.

Although the Shannon entropy has been used to quantitatively assess uncertainties of hydrologic variables, models of water resources systems, and their parameters (Singh 1997; Harmancioglu and Singh 1998), it has rarely been applied to drought events and risk assessment of water security. Drought entropy is a measure of uncertainties of the water supply system when drought occurs. It also indicates valid information obtained by the water supply system. The amount of obtained information is one of the factors determining the importance and reliability evaluations of certain systems, such as the water supply system. Thus, the above weightsiω (i=1, 2, 3) can be determined objectively by means of drought entropy.

Suppose M is the number of assessment alternatives, L is the number of assessment indices, and X = (xij)M×Lis the original data matrix, where xijis the value of the jth index of the ith assessment alternative. The steps in obtaining the weights based on drought entropy (Dong et al. 2010) are as follows:

Step 1: The original matrix is standardized. Suppose R = (rij)M×Lis the standardized result of the original matrix X, where, for benefit-typed indices we have

and for cost-typed indices, we have

Step 2: Drought entropy of assessment indices is determined. The frequency of the ith assessment alternative and the drought entropy of the jth index are defined as follows:

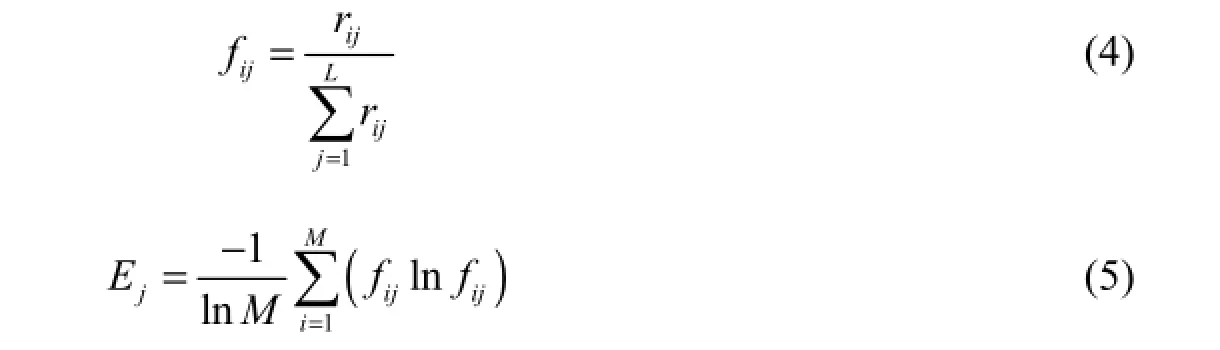
where fijis the frequency of the ith assessment alternative appearing during the generation of a drought hazard, its distribution representing the probabilistic characteristic of droughtevents of water security systems, and Ejis the drought entropy of the jth index, where the larger the value is, the lesser the contribution of the index to generating the hazard.

Step 3: Weights are determined. The weight of the jth index based on drought entropy is as follows:

where 0 ≤ ωj≤ 1 and

2.3 Brief introduction to D-S evidence theory and evidential reasoning algorithm

The D-S evidence theory was established by Shafer (1976) and Dempster (1967). In the D-S evidence theory, information is evidence to support the results of a decision and is not 100% reliable. In addition, the same pieces of evidence may have different contributions to eventual decision making because their weights are different; the weights reflect the relative importance of the evidence. Dempster’s combination rule, which is the foundation of the D-S evidence theory, is as follows:

Suppose m1and m2are two basic probability assignments on an identical frame of discernment based on two independent pieces of evidence; their respective focal elements are B1,B2,… ,Bkand C1,C2,… ,Cl.The new combined basic probability assignment can be obtained according to Dempster’s combination rule using Eq. (7):

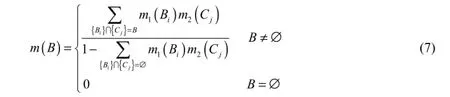
where B is the intersection of focal elements B1,B2,… ,Bkand C1,C2,… ,Cl; ∅ denotes a null set; i= 1,2,… ,k ; and j= 1,2,… ,l .

The evidential reasoning algorithm is based on a multi-attribute evaluation framework and the D-S theory. Without loss of generality, it is assumed that a risk assessment system of water security for drought periods has M alternatives, and each alternative is a status measurement of water security during drought periods in certain regions, denoted by ai( i = 1,2,… ,M ). The risk assessment system of water security during drought periods consists of one upper-level water security factor and L lower-level water security factors: ej( j= 1,2,… , L ) with relative weights W = {ω1,ω2,… ,ωL}. The lower-level water security factors are also called basic water security factors and their weights are obtained with Eq. (6).

The alternative ai(i = 1,2,… ,M ) is assessed to a grade Hnwith a belief degree ofaccording to the water security factors ej( j= 1,2,… ,L ). We denote this with a distributed assessmentwhich is considered a belief function. Hnrepresents the nth assessment grade of the set H (assuming H1is the worst assessment grade, H2is poor, H3is average, H4is good, and H5is the best). In a distributed assessment, it is required that(Wang et al. 2006).the assessment is said to be complete; otherwise, it is incomplete. If, the assessment is one of complete ignorance.

The recursive evidential reasoning algorithm that aggregates L basic attributes for alternative ai( i= 1,2,… ,M )was developed over the past decade (Yang 2001; Yang and Xu 2002a, 2002b; Wang et al. 2006) and is introduced briefly below.

First, the belief degrees are transformed into basic probability masses by combining the relative weights and the belief degrees using the following equations (Yang 2001):

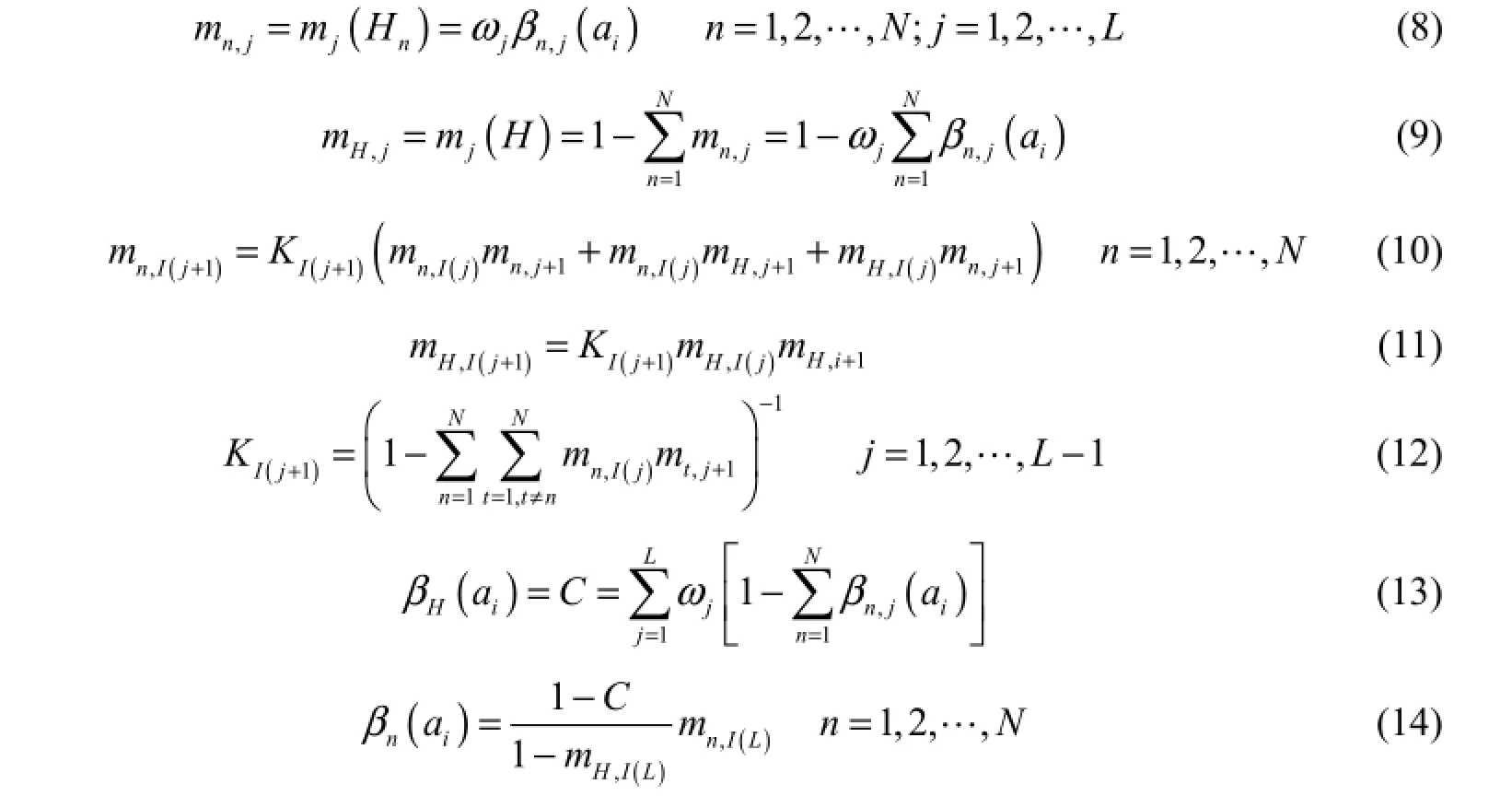
where mn,I(1)= mn,1(n = 1,2,… , N ) and mH,I(1)=mH,1; mn,jrepresents the basic probability mass of aibeing assessed at the assessment grade Hnaccording to the basic water security factor ej; mH,jis not assigned to any individual grades for a certain alternative ai; mn,I(j+1)is a basic probability mass for grade Hnafter integration of the basic water security factor ej; K is a normalization factor; βH( ai) is the unassigned belief degree of any grades on ai; and βn( ai) is the belief degree for grade Hnof ai.

This evidential reasoning algorithm is not only used in a quantitative multi-attribute assessment problem, but also adapted to the qualitative decision problem (Yang 2001), and the quantitative attribute value can be transformed into an equivalent expectation so that thecombination rule of the D-S theory and evidential reasoning algorithm can be used. Assuming that the grade { H1, H2,H3,H4,H5} corresponds to the set {0, 0.25, 0.5, 0.75, 1} and the basic water security factor ejis a profit attribute, then a value hifor ejmay be represented using the following formula (Yang 2001):

where

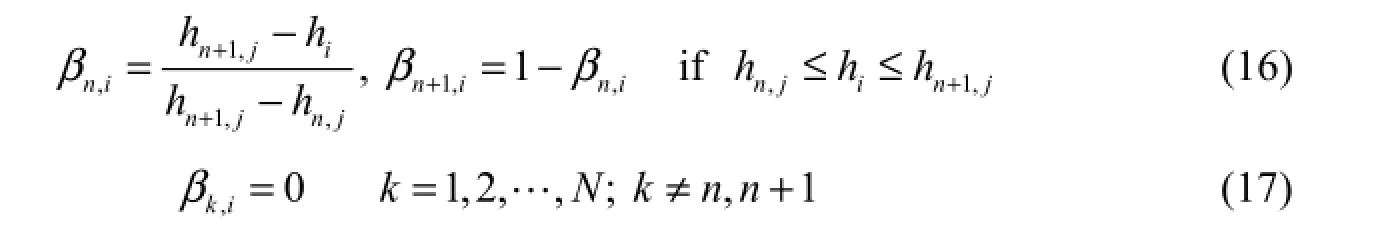
To rank the alternatives, as described by the utility in the intervals, the utility is the preference of the decision maker and is denoted by u(Hn) for the utility of an evaluation grade Hn. Then, the utility of the assessment is obtained with the expected utility of the expectation in the evidential reasoning algorithm, as defined by the following equation:

Therefore, the alternatives can be ranked according to their utilities in the evidential reasoning algorithm.

2.4 Water security assessment during drought periods in evidential reasoning algorithm

Less is known about droughts than floods, as droughts are complex, and it is difficult to identify all the uncertainty factors. Thus, risk assessment with the three indices mentioned above is uncertain or at least imprecise, because there is a degree of uncertainty in the values of the three indices that are obtained through simulation methods or other relevant approaches. To some extent, calculation of the DRI value can be regarded as one kind of information aggregation task, where the D-S evidence theory can work perfectly. The D-S evidence theory has been applied widely to computing the probability of occurrence of an event by integrating independent pieces of information (evidence) (Raje and Mujumdar 2010a). For example, Harp and Vesselinov (2012) utilized the D-S evidence theory to account for imprecise definitions of epistemic uncertainty and provide bounds of the facies probability map in the form of facies belief and plausibility maps; Fu and Kapelan (2011) represented the satisfaction degree of a water distribution network to measure the system performance in terms of the D-S evidence theory; and Raje and Mujumdar (2010b) chose the weighted D-S theory to combine future projections of the regional hydrologic variable in order to express beliefs in some hypotheses, describe uncertainty and ignorance in the system, and provide a quantitative measurement of belief and plausibility in results. Here, the D-S evidence theory and evidential reasoningalgorithm were used to assess water security risks during drought periods. Under the evidential reasoning algorithm, Eq. (1) can be revised as follows:

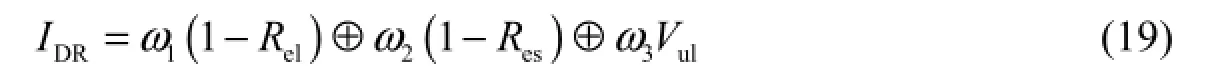
where ⊕ is the operator of aggregation, and the values of IDRare regarded as the utilities of different alternatives.

3 Case study

3.1 Study area

North China has complex natural conditions, intensive human activities, and highly-demanded water resources. Just as described in the well-known saying, “Nine droughts in ten years”, the frequency of drought remained at a high level in North China, notably in the Haihe River Basin (Xia 2002). Drought in the Haihe River Basin has become an urgent issue as its high frequency is caused by the continuous decrease of precipitation and the rapid growth in population. What’s worse, drought has become a bottleneck for social and economic development in this area. Therefore, risk assessment of drought should be one of the most important factors in decisions regarding sustainable development in this area.

The Haihe River Basin consists of four parts: the Luanhe River Basin, the North of Haihe River Basin, the South of Haihe River Basin, and the Tuhaimajia River Basin. Table 1 shows all risk indices during drought periods in the Haihe River Basin for different alternatives, and the data on reliability, resiliency, and vulnerability come from Zhang et al. (2005), who simulated super-long (10 000-year) annual runoff at regions in the Haihe River Basin randomly based on observed runoff from 1956 to 1998, with the mean annual runoff as the truncation level. In Table 1, different regions of the Haihe River Basin are marked as different alternatives; each alternative represents one region. The objective was to obtain the value of the DRI according to Eq. (19), so we first need to obtain the weights of the three indices. Following Eqs. (4) through (6) based on drought entropy, the weights of the three indices 1−Rel, 1 −Res, and Vul, were obtained: ω1= 0.32, ω2= 0.40, and ω3= 0.28.

Table 1 Comparison of risk indices during drought periods in Haihe River Basin for different alternatives

3.2 Calculating steps of DRI value

The original indices of reliability, resiliency, and vulnerability are weighted evidence to support the DRI, assuming the given three indices are all assessed on the same assessment grade H ={H1,H2,H3,H4,H5}. The DRI value of each alternative can be obtained by Eqs. (8)through (14). Taking alternative1A as an example, the calculation steps are as follows:

Step 1: Quantitative data of basic water security factors are transferred to obtain basic probability masses:

A1has three indices, and grade H ={H1,H2,H3,H4,H5}corresponds to the set {0, 0.25, 0.5, 0.75, 1}. The values of the three indices are {0.57, 0.58, 0.36}, because 0.5 ＜ 0.57 ＜ 0.75, so the belief degree of H3isthe belief degree of H4is 0.28, and the belief degrees of A1can be obtained:

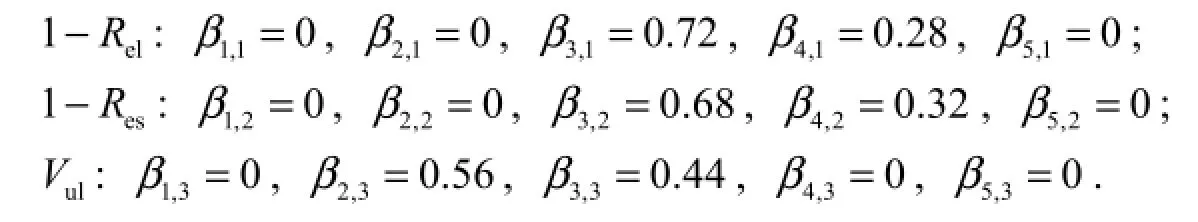
Note that the belief degrees of each index are complete, because 0.72 + 0.28 = 1, 0.68 + 0.32 = 1, and 0.56 + 0.44 = 1. Given the weights of the three indices and Eqs. (8) and (9), the basic probability masses for alternative A1are obtained:

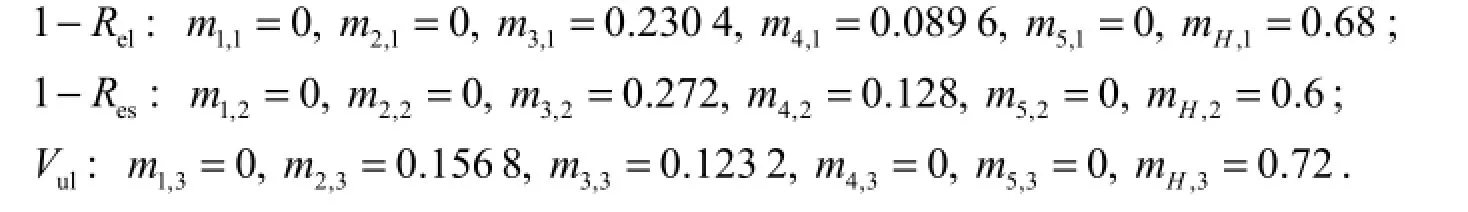
Step 2: The indices in evidential reasoning algorithm are aggregated:

Because there are three indices in each alternative, the aggregation of three indices must be combined twice. Index 1 −Reland index 1 −Resaggregate first, and the results of their aggregation are combined with Vulagain. Since

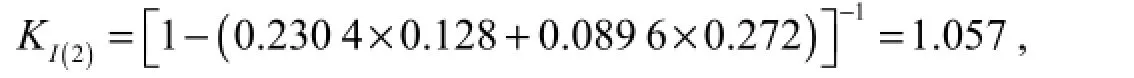
we then have

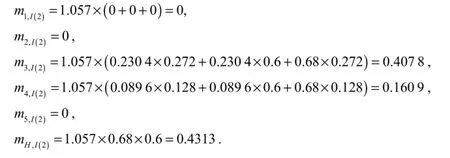
Since

we also have

Step 3: The utility of the alternative is calculated:

Because the belief degree of each index is complete, C= 0 when using Eq. (13), so the combined degrees of belief for the alternativeA1are obtained using Eq. (14) as follows:

The utility of alternative A1is obtained using Eq. (18) as follows:

u(A1) = 0 × 0 + 0.1165 × 0.25 + 0.6839 × 0.5 + 0.1996 × 0.75 + 0× 1 = 0.520 8.

4 Results and discussion

Other alternatives can also be aggregated in the same way as1A. Here, we consider two scenarios: one uses the equal weights to obtain the DRI value based on the evidential reasoning algorithm, and the other uses drought entropy weights to obtain the DRI value, also based on the evidential reasoning algorithm. Thus, the values of the DRI for each alternative under the two scenarios are shown in Table 2. The results of the two scenarios are consistent with the original results obtained by Zhang et al. (2005), and the orders of every alternative remain invariant under two scenarios.

Table 2 Comparison of DRI values of different scenarios

The DRI values of each alternative, revealing the risk degree of water security, imply a severe water shortage problem in the Haihe River Basin (Table 2). To validate the values of the DRI based on drought entropy and the evidential reasoning algorithm, comparison between the evidential algorithm and the original method provided by Zhang et al. (2005) wasconducted. The first comparison was conducted between the original values of the DRI and the values of the DRI obtained with the evidential reasoning algorithm, with both under equal weight, for ω1, ω2, and ω3. Table 2 shows that the results of DRI values of the original method and the evidential reasoning algorithm are highly consistent with each other, though it should be pointed out that the latter values are a little larger than the former except for alternative A3, and that the DRI value of A3using the evidential algorithm is slightly smaller than the original value of the DRI. The reason why the latter values of the DRI are larger than the former may be that the latter results have taken uncertainties of drought into account, and this consideration should reveal the real risk in practice. It is also suggested that the drought risk status of the North of Haihe River Basin (A2) is best, or safest, whether under the original condition or evidential algorithm conditions, while the drought risk status of the Tuhaimajia River Basin is the worst, as proven by the fact that it has the highest vulnerability index among the different alternatives. This comparison demonstrates that the approach using the evidential reasoning algorithm is valid and reliable, and the results obtained with the evidential reasoning algorithm would be more precise and accord with the real facts of the Haihe River Basin because the original values of the DRI may be underestimated, without consideration of uncertainties in water security during drought periods.

Another DRI comparison was conducted between the equal weights and the weights derived from drought entropy (entropy weight) for ω1,ω2, and ω3using the evidential reasoning algorithm. The values of the DRI for each alternative based on drought entropy become larger than the equal weight values for the same evidential reasoning algorithm, which implies that the weights of the three indices have a significant impact on the values of the DRI. The values of the DRI for each alternative are more objective and scientific than the equal weight values because of the utilization of drought entropy. In particular, the increments of the DRI values for A1, A2, and A3under theentropy weight and evidential algorithm scenario are larger than they are under the equal weight and evidential algorithm scenario corresponding to the original DRI values, except that A4increases slightly. The invariant order of the DRI from A1to A4demonstrates the practical situation of different alternatives resulting from the difference of indices for respective alternatives, and the feasibility and validity of the approach of drought entropy weights and the evidential reasoning algorithm can be proven indirectly.

Considering the complexities of drought (Rui et al. 2013), uncertainty factors in water security during drought periods have not been described explicitly and quantitatively. Thus, further research will focus on description and calculation of uncertainties related to drought. Above all, when uncertain factors of water security during drought periods in the Haihe River Basin are considered, the values of the DRI become larger and the status of water security worsens, because the DRI results demonstrate the status of water security and depicts the real risk conditions. Thus, water security risks during drought periods in the Haihe River Basin under deterministic conditions may be underestimated and need more attention.

5 Conclusions

The concept of drought entropy is presented in this paper in order to determine weights of the three indices of reliability, resiliency, and vulnerability. The drought entropy was also used to obtain the weights in a study of the Haihe River Basin. The D-S evidence theory and evidential reasoning algorithm are introduced to consider the uncertainties during risk assessment of water security, and the three indices are regarded as supporting evidence for the DRI. The DRI value was redesigned and calculated under uncertainty conditions. According to the comparison of the DRI values of two scenarios, the preliminary conclusions can be summarized as follows:

(1) The drought entropy can be used to determine the weights of the three indices of reliability, resiliency, and vulnerability, and should have wide application. Although the D-S evidence theory and evidential reasoning algorithm are suited to solving the quantitative and qualitative data aggregation problems, they are powerful tools for dealing with imprecise, incomplete, and uncertain assessment problems, and they are valid for coping with risk assessment of water security during drought periods.

(2) The value of the DRI in risk assessment of water security during drought periods may be underestimated without consideration of uncertainties from the case study of the Haihe River Basin, and it may require more attention to uncertainties related to drought.

(3) The status of water security during drought periods in the Haihe River Basin is very severe and requires more attention and observation in order to mitigate consequent losses.

Cancelliere, A., Ancarani, A., and Rossi, G. 1998. Susceptibility of water supply reservoirs to drought conditions. Journal of Hydrologic Engineering, 3(2), 140-148. [doi:10.1061/(ASCE)1084-0699(1998) 3:2(140)]

Chung, C. H., and Salas, J. D. 2000. Drought occurrence probabilities and risk of dependent hydrologic processes. Journal of Hydrologic Engineering, 5(3), 259-268. [doi:10.1061/(ASCE)1084-0699(2000) 5:3(259)]

Dempster, A. P. 1967. Upper and lower probabilities induced by a multivalued mapping. The Annals of Mathematical Statistics, 38(2), 325-339. [doi:10.1214/aoms/1177698950]

Dong, Q. J., Ai, X. S., Cao, G. J., Zhang, Y. M., and Wang, X. J. 2010. Study on risk assessment of water security of drought periods based on entropy weight methods. Kybernetes, 39(6), 864-870. [doi:10.1108/ 03684921011046627]

Fu, G. T., and Kapelan, Z. 2011. Fuzzy probabilistic design of water distribution networks. Water Resources Research, 47(5), W05538. [doi:10.1029/2010WR009739]

Hashimoto, T., Loucks, D. P., and Stedinger, J. R. 1982a. Robustness of water resources systems. Water Resources Research, 18(1), 21-26. [doi:10.1029/WR018i001p00021]

Hashimoto, T., Stedinger, J. R., and Loucks, D. P. 1982b. Reliability, resiliency, and vulnerability criteria for water resources system performance evaluation. Water Resources Research, 18(1), 14-20. [doi:10.1029/ WR018i001p00014]

Harmancioglu, N. B., and Singh, V. P. 1998. Entropy in environmental and water resources. Herschy, R.W., and Fairbridge, R.W., eds., Encyclopedia of Hydrology and Water Resources, 225-241. Dordrecht: Kluwer Academic Publishers.

Harp, D. R., and Vesselinov, V. V. 2012. Analysis of hydrogeological structure uncertainty by estimation of hydrogeological acceptance probability of geostatistical models. Advances in Water Resources, 36, 64-74. [doi:10.1016/j.advwatres.2011.06.007]

Huang, W. C., and Chou, C. C. 2008. Risk-based drought early warning system in reservoir operation. Advance in Water Resources, 31(4), 649-660. [doi:10.1016/j.advwatres.2007.12.004]

Jinno, K., Xu, Z. X., Kawamura, A., and Tajiri, K. 1995. Risk assessment of a water supply system during drought. International Journal of Water Resources Development, 11(2), 185-204. [doi:10.1080/ 07900629550042399]

Kao, S. C., and Govindaraju, R. S. 2010. A copula-based joint deficit index for droughts. Journal of Hydrology, 380(1-2), 121-134. [doi:10.1016/j.jhydrol.2009.10.029]

Loáiciga, H. A. 2005. Drought, tree rings, and reservoir design. Journal of the American Water Resources Association, 41(4), 949-958. [doi:10.1111/j.1752-1688.2005.tb03779.x]

Loáiciga, H. A., and Leipnik, R. B. 1996. Stochastic renewal model of low-flow stream flow sequences. Stochastic Hydrology and Hydraulics, 10(1), 65-85.[doi:10.1007/BF01581794]

Lowrance, W. W. 1976. Of Acceptable Risk: Science and the Determination of Safety. Los Altos: William Kaufmann.

Merabtene, T., Kawamura, A., Jinno, K., and Olsson, J. 2002. Risk assessment for optimal drought management of an integrated water resources system using a genetic algorithm. Hydrological Processes, 16, 2189-2208. [doi:10.1002/hyp.1150]

Mondal, M. S., and Wasimi, S. A. 2007. Evaluation of risk-related performance in water management for the Ganges delta of Bangladesh. Journal of Water Resources Planning and Management, 133(2), 179-187. [doi:10.1061/(ASCE)0733-9496(2007)133:2(179)]

Moy, W. S., Cohon, J. L., and Revelle, C. S. 1986. A programming model for analysis of the reliability, resiliency, and vulnerability of water supply reservoir. Water Resources Research, 22(4), 489-498. [doi:10.1029/WR022i004p00489]

Raje, D., and Mujumdar, P. P. 2010a. Hydrologic drought prediction under climate change: Uncertainty modeling with Dempster-Shafer and Bayesian approaches. Advances in Water Resources, 33(9), 1176-1186. [doi:10.1016/j.advwatres.2010.08.001]

Raje, D., and Mujumdar, P. P. 2010b. Constraining uncertainty in regional hydrologic impacts of climate change: Nonstationarity in downscaling. Water Resources Research, 46(7), W07543. [doi:10.1029/ 2009WR008425]

Rowe, N. 1977. Risk: An Anatomy of Risk. New York: Wiley.

Rui, X. F., Liu, N. N., Li, Q. L., and Liang, X. 2013. Present and future of hydrology. Water Science and Engineering, 6(3), 241-249. [doi:10.3882/j.jssn.1674-2370.2013.03.001]

Shang, S. H., and Wang, H. J. 2013. Assessment of impact of water diversion projects on ecological water uses in arid region. Water Science and Engineering, 6(2), 119-130. [doi:10.3882/j.jssn.1674-2370. 2013.02.001]

Shannon, C. E. 1948. A mathematical theory of communication. Bell System Technical Journal, 27(3), 379-423. [doi:10.1145/584091.584093]

Shafer, G. 1976. A Mathematical Theory of Evidence. New Jersey: Princeton University Press.

Singh, V. P. 1997. The use of entropy in hydrology and water resources. Hydrological Processes, 11(6), 587-626. [doi:10.1002/(SICI)1099-1085(199705)11:6＜587::AID-HYP479＞3.3.CO;2-G]

Srdjevic, B., and Obradovic, D. 1995. Reliability-risk concept in evaluating control strategies for multireservoir water resources system. Roberts, P. D., and Ellis, J. E., eds., Large Scale Systems: Theory and Applications, 609-613. London: Elsevier.

Sun, R., Huang, H. Z., and Miao, Q. 2008. Improved information fusion approach based on D-S evidence theory. Journal of Mechanical Science and Technology, 22(12), 2417-2425. [doi:10.1007/s12206-008-0801-2]

Wang, Y. M., Yang, J. B., and Xu, D. L. 2006. Environmental impact assessment using the evidential reasoning approach. European Journal of Operational Research, 174(3), 1885-1913. [doi:10.1016/j.ejor.2004.09.059]

World Meteorological Organization (WMO). 1999. Comprehensive Risk Assessment for Natural Hazards. WMO.

Xia, J. 2002. A perspective on hydrological base of water security problem and its application study in north China. Progress in Geography, 21(6), 517-526. (in Chinese).

Yang, J. B. 2001. Rule and utility based evidential reasoning approach for multiattribute decision analysis under uncertainties. European Journal of Operational Research, 131(1), 31-61. [doi:10.1016/S0377-2217(99)00441-5]

Yang, J. B., and Xu, D. L. 2002a. On the evidential reasoning algorithm for multiattribute decision analysis under uncertainty. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 32(3), 289-304.

Yang, J. B., and Xu, D. L. 2002b. Nonlinear information aggregation via evidential reasoning in multiattribute decision analysis under uncertainty. IEEE Transactions on Systems, Man, and Cybernetics, Part A: Systems and Humans, 32(3), 376-393.

Zamani, G. H., Marjan, J. G., and Kiumars, Z. 2006. Coping with drought: Towards a multilevel understanding based on conservation of resources theory. Human Ecology, 34(5), 677-692. [doi:10.1007/s10745-006-9034-0]

Zhang, X., Xia, J., and Jia, S. F. 2005. Water security of drought period and its risk assessment. Journal of Hydraulic Engineering, 36(9), 1138-1142. (in Chinese)

(Edited by Yun-li YU)

This work was supported by the National Natural Science Foundation of China (Grants No. 51190094, 50909073, and 51179130) and the Hubei Province Natural Science Foundation (Grant No. 2010CDB08401).

*Corresponding author (e-mail: dqjin@whu.edu.cn)

Received Jan. 13, 2013; accepted Nov. 11, 2013