Effect of upward seepage on bedload transport rate

Xiao-xie LIU, Yee-Meng CHIEW*

1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

2. School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

Effect of upward seepage on bedload transport rate

Xiao-xie LIU1, Yee-Meng CHIEW*2

1. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, P. R. China

2. School of Civil and Environmental Engineering, Nanyang Technological University, Singapore 639798, Singapore

The paper presents an investigation of injection effects on the bedload transport rate. According to dimensional analysis, two dimensionless groups, an Einstein’s parameter group and a modified densimetric Froude number group, were chosen to examine how injection affects the bedload transport rate. Experimental studies were conducted in an open-channel flume with an upward seepage zone. The sediment particles used for the test were 0.9 mm in diameter. The experimental results show that an increase in the injection velocity causes a reduction in the shear velocity excess, which is defined as the difference between the shear and critical shear velocities, leading to a reduction in the bedload transport rate. The equation for predicting the bedload transport rate in the presence of upward seepage was derived empirically. The proposed prediction method is suitable for engineering practice, since it only requires the undisturbed flow condition, properties of sediment particles, and the injection velocity.

upward seepage; bedload transport rate; shear velocity; shear stress; open-channel flow

1 Introduction

Unlike many manmade canals that are constructed with impermeable material such as concrete, natural alluvial rivers almost inevitably have a permeable boundary. This is due to the porosity in natural materials, either in the form of gravels, sand, silt, or clay. The degree of porosity is dependent on the size, shape, and distribution of the bed and bank materials. Water will often seep through the permeable boundary if there is a difference between the free surface in a river and the adjoining groundwater table. Depending on the direction of the groundwater flow, seepage normal to the boundary can be either in the form of injection (seepage through a channel in the upward direction) or suction (seepage through a channel in the downward direction). The mass and momentum transfers induced by seepage have a significant influence on the flow characteristics and sediment transport behaviors. Generally, the effect of seepage on sediment particle mobility can be divided into three categories, namely, seepage effects on the bed shear stress, critical shear stress, and sediment transport rate.

There are two forces that govern sediment particle movement in a river: the driving forceand resistant force. On the one hand, the driving force is induced by the friction between the flow and sediment bed, which can be represented by the bed shear stress. In the presence of seepage across the sediment bed, many investigators (Oldenziel and Brink 1974; Maclean 1991; Cheng and Chiew 1998; Chen and Chiew 2004; Dey and Nath 2010; Dey et al. 2011) have shown that an upward seepage or injection reduces the bed shear stress, whereas a downward seepage or suction has the opposite effect. The reduction of the bed shear stress with injection is due to the modification of the near-bed flow configuration (Krogstad and Kourakine 2000). In contrast, suction brings high-momentum fluid nearer to the bed, thereby increasing the bed shear stress. Lu et al. (2008) and Liu and Chiew (2012) have provided a summary of these studies.

On the other hand, the resistant force acting on the sediment particle can be represented by the critical shear stress, which is defined as the shear stress needed to initiate sediment entrainment. A single cohesionless particle subjected to seepage will clearly experience an additional seepage force. With injection, the particle is subjected to an upward seepage force. Therefore, the particle becomes lighter and is more easily entrained, resulting in a reduction of the critical shear stress. In the same way, suction induces a downward force, inhibiting particle movement and causing an increase of the critical shear stress. This behavior is explicitly and implicitly discussed in many published studies, e.g., Cheng and Chiew (1999), Dey and Zanke (2004), Xie et al. (2009), and Kavcar and Wright (2009). To this end, Cheng and Chiew (1999) and Liu and Chiew (2012) obtained theoretical equations that were verified using laboratory data for the computation of the critical shear stress of sediment particles subjected to injection and suction, respectively.

Generally, the movement of sediment particles, represented by the sediment transport rate, is related to the difference between the driving and resistance forces acting on the sediment particles, known as the excess net force, Fnet. When Fnetis less than zero, the particles will not move and the sediment transport rate is zero; when Fnetis equal to zero, the particles are just about to move, a state customarily known as the threshold or critical condition; and when Fnetis larger than zero, the sediment particles are in motion. Since the driving force and resistant force acting on the bed particles can be represented by the bed and critical shear stresses, respectively, the sediment transport rate can also be expressed as a function of the difference between these two stresses, which is commonly called the shear stress excess. As discussed in the preceding paragraphs, injection causes a reduction in both the bed and critical shear stresses, while suction has the completely opposite effect. Consequently, the stability of the bed particles or their transport rate is clearly dependent on the dominant effect. For instance, in the case of injection, if the reduction of bed shear stress exceeds that of the critical shear stress, i.e., the shear stress excess decreases, the sediment transport rate will decrease. So far, the response of sediment movement to the variation of shear stress excess induced by seepage has not been clearly understood by researchers, leading to contradiction and uncertainy in thepublished results. For example, some researchers (Oldenziel and Brink 1974; Richardson et al. 1985; Francalanci et al. 2008) have stated that injection increases the sediment transport rate whereas suction decreases it. However, other researches (Willetts and Drossos 1975; Maclean 1991; Lu and Chiew 2007; Rao et al. 2011; Liu and Chiew 2012) have presented an exactly opposite conclusion, stating that suction has a tendency to reduce the stability of bed particles, while injection decreases particle mobility on a transporting bed. Liu and Chiew (2012) have presented an extensive review of these studies.

In order to improve our understanding of the influence of upward seepage or injection on the sediment transport behavior, an experimental study was conducted in a laboratory flume that contained a permeable bed. Moreover, some published equations (Engelund and Hansen 1967; Yalin 1977) for predicting the bedload transport rate in the presence of an impermeable boundary were fitted with laboratory data. Based on this, an empirical formula is presented for the prediction of the bedload transport rate with occurrence of injection based on the bedload transport rate directly measured from experiments.

2 Experiments

The experiments were conducted in the Hydraulic Laboratory at Nanyang Technological University. The flume was glass-sided, 30 m long, 0.7 m wide, and 0.6 m deep. The flow rate, which was controlled with a speed inverter and valve, was monitored using an electromagnetic flow meter. The flume consisted of a seepage zone in the form of a recess, which was 2 m long, 0.7 m wide, 0.4 m deep, and located at a distance of 16 m from the upstream end of the flume. Fig. 1 depicts the layout of the experimental setup and seepage recess. The flume was filled with uniformly distributed sand with a median grain size (d50) of 0.9 mm. The sand was placed on the top of a filter cloth, which, in turn, overlaid a perforated metal plate. A separate submersible pump was installed in the laboratory reservoir to generate injection; its flow discharge, regulated using a speed inverter and valve, was monitored with another flow meter. Water was allowed to seep through the perforated plate, filter cloth, and sand layer. Before commencement of an experiment, the sand surface in the test section was first leveled to the same elevation as the surface upstream and downstream of the test section. A sand trap, which was 35 cm long, 70 cm wide, and 5 cm deep, was placed immediately downstream of the seepage zone for collecting the transported sediment particles. This method, used for measuring the sediment transport rate, is similar to that adopted by previous researchers (Sumer et al. 2003; Pagliara et al. 2011, 2012).

The streamwise velocity profiles along the centerline of the flume for the undisturbed flow condition were measured using an 8 mm-diameter mini-propeller. The streamwise mean flow velocity without seepage, denoted as U0, was then determined by dividing the area of the velocity profile with the flow depth. The undisturbed mean flow velocity profiles at the beginning, mid-section, and downstream end of the seepage zone were measured, and theiraverage was calculated and used for further analyses. After the streamwise flow discharge was adjusted to the predetermined value, water was allowed to run for half an hour in the absence of injection. The sediment particles started to move and the sediment bed remained flat during this period. The injection pump was then turned on, and the seepage discharge gradually increased to the predetermined value. No bedforms with a significant height were observed during the experiments. Half an hour after turning on the pump, the cover of the sand trap was opened for collecting the transported sediment particles within a time duration ranging from 90 to 300 seconds, depending on the bedload transport rate. A peristaltic pump was used to suck out the trapped particles. The wet sediment particles collected were then put in a 120℃oven for 24 hours to reach the oven-dry condition. The dry sediment particles were weighed, and the volumetric sediment transport rate per unit width, qb, was then calculated with its known bulk density ρb. The experiment was repeated three times for each test, and the average value of qbwas computed for further analyses. A total of 86 tests with different flow rates and injection velocities were conducted in this study.

Fig. 1 Schematic diagrams of open-channel flume and seepage zone (not to scale)

3 Dimensional analysis

Based on energy considerations such as the stream-power concept, Engelund and Hansen (1967) derived a total load discharge formula in the absence of seepage as follows:

where Φ is Einstein’s parameter;is the specific gravity, andwhere ρ is the fluid density, andis the density of sediment particles; g is the gravitational acceleration;is the Shields parameterwithout seepage, andandis the shear velocity without seepage. One may infer from Eq. (1) that the bedload transport rate with an impermeable boundary can be expressed as a function of the variables listed as follows:

According to the logarithmic law of open-channel flow, u*0is related to U0. Hence, Eq. (2) can be reduced to

When injection is introduced, the sediment transport rate should also be affected by the injection velocity Vs, the porosity of the sand medium n, and its coefficient of permeability K. Hence, they should be included in the equation. Eq. (3) is transformed as follows:

Note that the fluid viscosity, which is customarily used in this type of analysis, is excluded here because it has been found that its influence is negligible in the case of fully developed turbulence, which is the case in the present study. For this reason, it is also excluded from the list in Eq. (4). Using the Buckingham pi theorem, six pi terms were obtained, as follows:

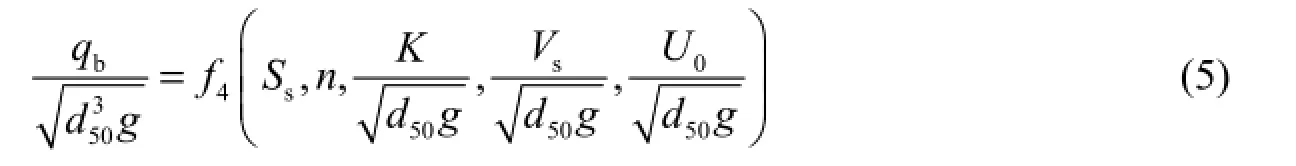
By applying simple algebra to the six pi terms in Eq. (5), they may be rearranged into two dimensionless groups, as follows:

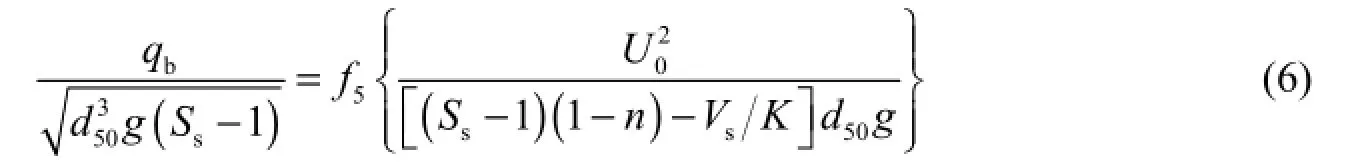
The dimensionless term on the left side of the equation,is the well-known Einstein’s parameter, Φ, which has been widely used as the dimensionless volumetric sediment transport rate in many previous studies. The second dimensionless term,is a modified densimetric Froude number, denoted by Ω. The modifieris used to account for injection and porosity effects. In the absence of these two effects, a condition that signifies an impermeable bed, i.e., n = 0 and Vs= 0, Ω simply decreases to the commonly used densimetric Froude number, which isIn the following section, the experimental results are presented in order to investigate the empirical relationship between Φ and Ω.

4 Results and discussion

Table 1 shows the properties of sediment particles used in this study, in whichwith ν denoting the kinematic viscosity of water; u∗c0is the critical shear velocity without seepage; and Vscis the injection velocity at the quickest conditions, at which sand loses its weight due to the upward seepage. The critical shear velocity without seepage, u∗c0, is computed using the Shields function presented in van Rijn (1984):

where τ∗c0is the critical Shields parameter without seepage, and

Table 1 Pertinent parameters of sediment particles in this study

The undisturbed flow conditions of all the tests are summarized in Table 2, in which h0is the water depth without suction, and Q0is the undisturbed streamwise flow rate. Series 1 can be considered the threshold condition as the value of u*0u∗c0≈ 1. The initial conditions of series 2 and 3 are transporting beds in the absence of seepage since the corresponding value of u*0u∗c0＞ 1.

Table 2 Undisturbed flow conditions of each series

The bedload transport rate,qb, was measured by varying both the undisturbed flow rate and injection velocity, where the injection velocity is denoted as a positive value. The measured bedload transport rates varying with Vsat different values of τ*0are plotted in Fig. 2. All the data in the three series in Fig. 2 show the same trend. For the same undisturbed flow condition, the increase of the injection velocity leads to a reduction in the bedload transport rate. For series 1, when the injection velocity increases from 0 to 0.25 cm/s, the bedload transport rate decreases by a maximum of about 30%, i.e., from 0.05 × 10−6m2/s to 0.035 × 10−6m2/s. For the same increment of injection velocity, the sediment transport rate of series 2 decreases by a maximum of about 33%, i.e., from 0.12 × 10−6m2/s to 0.08 × 10−6m2/s. The sedimenttransport rate of series 3 decreases by a maximum of about 40%, i.e., from 0.25 × 10−6m2/s to 0.15 × 10−6m2/s. It may be inferred from the results that the reduction of the bedload transport rate becomes more apparent for higher τ*0values.

Fig. 2 Relationships of qband Vsfor differentundisturbed flow conditions

4.1 Effect of injection on shear velocity excess

Cheng and Chiew (1998) had shown that the bed shear stress decreases with the injection velocity. They derived a modified logarithmic law using the turbulence kinetic energy equation to account forthe effect of upward seepage on the velocity distribution in the open-channel flow, in which the shear velocity with seepage, u*s, is related to the depth-averaged flow velocity U, water depth h, boundary roughness ks, and injection velocity Vs, as follows:

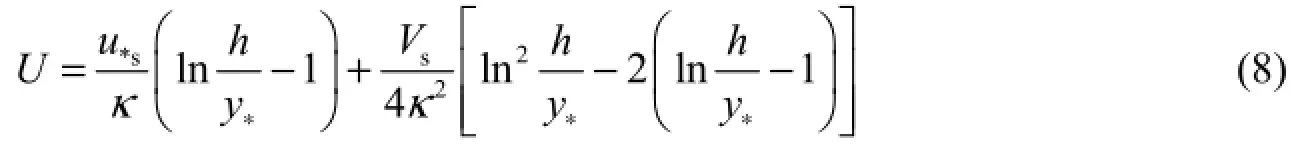
whereκis von Karman’s constant, and y∗= ksexp (− κ Rf), with Rf=8.5(1 +Vsu*s).

Additionally, Cheng and Chiew (1999) showed that the critical shear velocity, ucs, decreased in the presence of upward seepage or injection. The ratio of the critical shear velocity with seepage to that without seepage is expressed as a function of the ratio of the injection velocity to its value under the quickest conditions, as follows:

Based on the results of the work by Cheng and Chiew (1998, 1999), both the shear velocity and critical shear velocity decrease with an increase in the injection velocity. If the shear velocity excess, u*s−u*cs, decreases, the difference between the driving force and resistance force becomes smaller, and the sediment particles will move slower. If u*s−u*csdecreases to a negative value, the sediment bed becomes immobile, and the sediment particle will not move. In other words, bed stabilityincreases with a reduction in the shear velocity excess. Since the present experimental observations show that the sediment particles move slower in the presence of injection, it may be inferred that the reduction in the shear velocity must have exceeded that of the critical shear velocity, resulting in an overall decrease in the shear velocity excess, u*s−u*cs. The measured data, which show that the bedload transport rate decreases with injection, are simply a corollary of this fact.

A quantitative illustration using several measured data is presented here to corroborate this phenomenon. The shear and critical shear velocities for two arbitrary injection velocities of Vs= 0.072 cm/s and 0.251 cm/s for series 1 to 3 were computed using Eqs. (8) and (9). The results are tabulated in Table 3, and clearly show that both the shear and critical shear velocities decrease with injection for all the three u∗0u∗c0values tested. Moreover, the shearvelocity excess also decreases with an increase in the injection velocity. For example, for the no-seepage condition, the shear velocity excess for series 3 ( u∗0u∗c0= 1.28) is 0.60 cm/s, meaning that the sediment is being transported. The shear velocity decreases to 2.026 cm/s when the injection velocity increases to 0.251 cm/s. At the same time, the critical shear velocity also decreases to 1.715 cm/s. The resulting shear velocity excess now becomes 0.31 cm/s, showing that the sediment bed is less mobile and the sediment particles move slower. With reference to series 1 ( u*0u*c0= 0.99), the shear velocity excess u*0−u*c0=− 0.01 cm ≈ 0cm/s when Vs= 0, i.e., the sediment bed is at the threshold condition, and therefore the bed particle is just about to move. When the injection velocity increases to 0.072 cm/s, the shear and critical shear velocities decrease to 1.902 cm/s and 2.040 cm/s, respectively. The resulting shear velocity excess now becomes −0.14, showing that the sediment bed has now become immobile. When the injection velocity increases further to 0.251 cm/s, the shear velocity excess further decreases to –0.36 cm/s, showing that the sediment bed has become more stable and the sediment particles are not moving as easily.

Table 3 Shear velocity excess with different injection velocities

Table 3 shows that the same inference may be drawn from the data associated with series 2 (u*0u*c0= 1.17). The illustration given here using the data in Table 3 confirms that injection reduces both the shear and critical shear velocities, but the overall result is a reduction in the shear velocity excess, and hence a decrease in the bedload transport rate. These results support the experimental observations that, under the same undisturbed flow conditions, the mobility of the sediment bed decreases with injection.

4.2 Determination of empirical function of Φ with occurrence of injection

In order to normalize the sediment transport rate measured under different undisturbed flow conditions, Einstein’s parameter without seepage, Φ0, and the modified densimetric Froude number without seepage, Ω0, were introduced as the respective normalizing parameters. To this end, the ratio of Einstein’s parameter with injection to that without injection, Φ/Φ0, is plotted as afunction of the ratio of the modified densimetric Froude number in the absence of injection to that in the presence of injection, Ω0/Ω, in Fig. 3.

Fig. 3 shows that the measurement results of Φ/Φ0for all three series tested generally collapse to form a smooth curve when plotted againstΩ0/Ω. The coordinate with Ω0/Ω and Φ/Φ0equal to 1 refers to the condition without occurrence of injection or seepage. Fig. 3 clearly reveals how reduction in Ω0/Ω or increase in injection velocity causes a reduction in Φ/Φ0or a decrease in sediment transport rate.

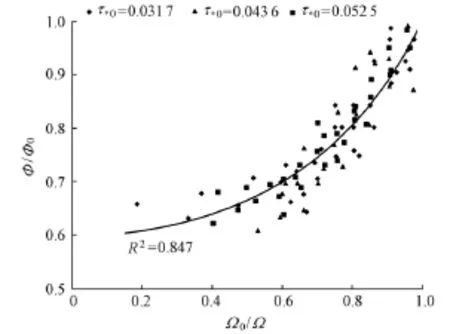
Fig. 3 Relationship between Φ/Φ0and Ω0/Ωfor sediment bed subjected to injection

By empirically fitting the experimental data, the relationship between Φ/Φ0and Ω0/Ω is obtained as follows:

The above equation is valid for, with an R2value of 0.847. It must be noted that this relationship is only valid for the condition before the onset of the quickest condition, which is defined as the situation when the upward seepage force just balances the downward weight force. The effect of injection at and beyond the quickest condition is not within the scope of this study. Even at the highest injection velocity in this test= 0.66. This means that sediment particles only move slowly at this injection velocity and the threshold condition for sediment entrainment is not reached.

5 Conclusions

Laboratory experiments were conducted to investigate injection effects on the bedload transport rate. The experimental results show that the shear velocity excess, which is defined as the difference between the shear and critical shear velocities, decreases with the increase of the injection velocity, resulting in a reduction in the bedload transport rate.

Based on dimensional analysis, Einstein’s parameter, was found to be a function of the modified densimetric Froude number Ω. The empirical equation for the prediction of the sediment transport rate was obtained based on the relationship between the ratio of Einstein’s parameter with injection to that without injection,, and the ratio of the modified densimetric Froude number in the absence of injection to that in the presence of injection,, which allows one to predict the sediment transport rate under given undisturbed flow conditions, properties of sand, and injection velocities.

Chen, X., and Chiew, Y. M. 2004. Velocity distribution of turbulent open-channel flow with bed suction. Journal of Hydraulic Engineering, 130(2), 140-148. [doi:10.1061/(ASCE)0733-9429(2004) 130:2(140)]

Cheng, N. S., and Chiew, Y. M. 1998. Modified logarithmic law for velocity distribution subjected to upwardseepage. Journal of Hydraulic Engineering, 124(12), 1235-1241. [doi:10.1061/(ASCE)0733-9429(1998) 124:12(1235)]

Cheng, N. S., and Chiew, Y. M. 1999. Incipient sediment motion with upward seepage. Journal of Hydraulic Research, 37(5), 665-681. [doi:10.1080/00221689909498522]

Dey, S., and Zanke, U. C. E. 2004. Sediment threshold with upward seepage. Journal of Engineering Mechanics, 130(9), 1118-1123. [doi:10.1061/(ASCE)0733-9399(2004)]

Dey, S., and Nath, T. K. 2010. Turbulence characteristics in flows subjected to boundary injection and suction. Journal of Engineering Mechanics, 136(7), 877-888. [doi:10.1061/(ASCE)EM.1943-7889. 0000124]

Dey, S., Sarkar, S., and Ballio, F. 2011. Double-averaging turbulence characteristics in seeping rough-bed streams. Journal of Geophysical Research F: Earth Surface, 116(3), F03020. [doi:10.1029/ 2010JF001832]

Engelund, F., and Hansen, E. 1967. A Monograph on Sediment Transport in Alluvial Streams. Copenhagen: Teknisk Forlag.

Francalanci, S., Parker, G., and Solari, L. 2008. Effect of seepage-induced nonhydrostatic pressure distribution on bed-load transport and bed morphodynamics. Journal of Hydraulic Engineering, 134(4), 378-389. [doi:10.1061/(ASCE)0733-9429(2008)134:4(378)]

Kavcar, P. C., and Wright, S. J. 2009. Experimental results on the stability of non-cohesive sediment beds subject to vertical pore water flux. Proceedings of the World Environmental and Water Resources Congress 2009, 3562-3571. Kansas City: American Society of Civil Engineers. [doi:10.1061/ 41036(342)359]

Krogstad, P.-Å., and Kourakine, A. 2000. Some effects of localized injection on the turbulence structure in a boundary layer. Physics of Fluids, 12(11), 2990-2999. [doi:10.1063/1.1314338]

Liu, X. X., and Chiew, Y. M. 2012. Effect of seepage on initiation of cohesionless sediment transport. Acta Geophysica, 60(6), 1778-1796. [doi:10.2478/s11600-012-0043-7].

Lu, Y., and Chiew, Y. M. 2007. Seepage effects on dune dimensions. Journal of Hydraulic Engineering, 133(5), 560-563. [doi:10.1061/(ASCE)0733-9429(2007)133:5(560)]

Lu, Y., Chiew, Y. M., and Cheng, N. S. 2008. Review of seepage effects on turbulent open-channel flow and sediment entrainment. Journal of Hydraulic Research, 46(4), 476-488. [doi:10.3826/jhr.2008.2942]

Maclean, A. G. 1991. Bed shear stress and scour over bed-type river intake. Journal of Hydraulic Engineering, 117(4), 436-451. [doi:10.1061/(ASCE)0733-9429(1991)117:4(436)]

Oldenziel, D. M., and Brink, W. E. 1974. Influence of suction and blowing on entrainment of sand particles. Journal of the Hydraulics Division, 100(7), 935-949.

Pagliara, S., Palermo, M., and Carnacina, I. 2011. Expanding pools morphology in live-bed conditions. Acta Geophysica, 59(2), 296-316. [doi:10.2478/s11600-010-0048-z]

Pagliara, S., Palermo, M., and Carnacina, I. 2012. Live-bed scour downstream of block ramps for low densimetric Froude numbers. International Journal of Sediment Research, 27(3), 337-350. [doi:10.1016/ S1001-6279(12)60039-0]

Rao, A. R., Sreenivasulu, G., and Kumar, B. 2011. Geometry of sand-bed channels with seepage. Geomorphology, 128 (3-4), 171-177. [doi:10.1016/j.geomorph.2011.01.003]

Richardson, J. R., Abt, S. R., and Richardson, E. V. 1985. Inflow seepage influence on straight alluvial channels. Journal of Hydraulic Engineering, 111(8), 1133-1147. [doi:10.1061/(ASCE)0733-9429(1985) 111:8(1133)]

Sumer, B. M., Chua, L. H. C., Cheng, N. S., and Fredsoe, J. 2003. Influence of turbulence on bed load sediment transport. Journal of Hydraulic Engineering, 129(8), 585-596. [doi:10.1061/(ASCE)0733-9429(2003)129:8(585)]

van Rijn, L. C. 1984. Sediment transport, Part I: Bed load transport. Journal of Hydraulic Engineering, 110(10), 1431-1456. [doi:10.1061/(ASCE)0733-9429(1984)110:10(1431)]

Willetts, B. B., and Drossos, M. E. 1975. Local erosion caused by rapid forced infiltration. Journal of the Hydraulics Division, 101(12), 1477-1488.

Xie, L., Lei, H., Yu, Y., and Sun, X. 2009. Incipient motion of riverbank sediments with outflow seepage. Journal of Hydraulic Engineering, 135(3), 228-233. [doi:10.1061/(ASCE)0733-9429(2009)135:3(228)]

Yalin, M. S. 1977. Mechanics of Sediment Transport. Oxford: Pergamon.

(Edited by Ye SHI)

*Corresponding author (e-mail: cymchiew@ntu.edu.sg)

Received Nov. 20, 2012; accepted Jun. 24, 2013