A method of determining nonlinear large strain consolidation parameters of dredged clays

Yu-peng CAO*, Xue-song Wang, Long DU Jian-wen Ding Yong-feng DENG

1. Institute of Geotechnical Engineering, Southeast University, Nanjing 210096, P. R. China

2. Municipal Facilities Authority, Weifang Economic Development Zone, Weifang 261057, P. R. China

A method of determining nonlinear large strain consolidation parameters of dredged clays

Yu-peng CAO*1,2, Xue-song Wang2, Long DU1, Jian-wen Ding1, Yong-feng DENG1

1. Institute of Geotechnical Engineering, Southeast University, Nanjing 210096, P. R. China

2. Municipal Facilities Authority, Weifang Economic Development Zone, Weifang 261057, P. R. China

A method of obtaining the large strain consolidation parameters of dredged clays considering the influence of the initial water content is investigated in this study. According to the test results of remolded clays with high initial water contents reported by Hong et al. (2010), a relationship between the void ratio (e) and effective stress (σ′) is established. Furthermore, based on the available permeability data from the literature, a new relationship between the permeability coefficient (k) and the ratio (e/eL) of the void ratio to the void ratio at the liquid limit (eL) is proposed. The new proposed expression considering the initial water content improves the e-k equation established by Nagaraj et al. (1994). Finally, the influence of the initial void ratio and effective stress on the large strain consolidation coefficient g(e) defined by Gibson et al. (1981) and k/(1+e) in large strain analysis is discussed. The results show that, under a constant effective stress, the value of k/(1+e) increases with the initial void ratio. The large strain consolidation coefficient shows the law of segmentation change, which decreases with the increase of the effective stress when the effective stress is less than the remolded yield stress, but increases rapidly with the effective stress when the effective stress is larger than the remolded yield stress.

initial void ratio; permeability; large strain consolidation parameter; remolded yield stress; dredged clay

1 Introduction

As methods of determining the coefficient of consolidation, the graphics-fitting method is not suitable for studying soil’s nonlinear consolidation properties, while the index property method cannot easily reflect soil’s consolidation characteristics accurately. A more accurate method of obtaining the coefficient of consolidation is calculation with the e-σ′ and e-k relationships, where e is the void ratio, σ′ is the effective stress, and k is the permeability coefficient. Davis and Raymond (1965) assumed that the permeability and compression coefficients changed synchronously, and deduced a constant consolidation coefficient. However, for most soils, the e-σ′ and e-k relationships do not change in the same pattern.

Burland (1990) normalized compression curves of remolded clays by introducing a newparameter called the void index. Taylor (1948) proposed that there was a semi-logarithmic relationship between the void ratio and permeability coefficient. Carrier et al. (1983) found that both e-σ′ and e-k showed a strong double logarithmic relationship. These studies improve our understanding of the soil’s compression and permeability characteristics, but the changing laws of the consolidation parameters above are based on traditional consolidation data and laboratory tests, where the initial void ratios are relatively low. In reclamation projects, the soil exhibits large strain consolidation characteristics at high initial water contents. Hence, it is necessary to study the compression and permeability characteristics under a high void ratio. By introducing the nonlinear relationships of e-σ′ and e-k into the consolidation theory proposed by Gibson et al. (1981), the large strain consolidation coefficient g(e) can be obtained. In Gibson’s theory, g(e) is constant, which leads to the difference between the calculated and real results. In order to reasonably reflect soil’s nonlinear consolidation characteristics, Zhang (2002) discussed the consolidation process by assuming that g(e) is in an exponential form. Jiang et al. (2010) pointed out that g(e) changed by an order of magnitude in the consolidation process. Though g(e) is a complex function of the void ratio, it can be fitted by a simple power function. In these studies, the initial void ratio was relatively high, but the influence of the initial void ratio was not taken into account.

Hong et al. (2010) conducted one-dimensional consolidation tests on clays reconstituted at different initial water contents, and found that the effect of the initial water content could not be ignored when studying soil’s compression characteristics. Note that there is a one-to-one correspondence between the initial water content and the initial void ratio for the same homogeneous saturated soil. Therefore, introducing the initial void ratio into soil’s consolidation analysis will reflect nonlinear consolidation characteristics more accurately.

In this study, according to the test results of remolded clays at high initial water contents and the concept of remolded yield stress reported by Hong et al. (2010), the relationship between the void ratio and effective stress considering the effect of the initial void ratio was established. Moreover, based on the available permeability data from the literature, a new e-k relationship is proposed, which expands the normalized e-k relation proposed by Nagaraj et al. (1994). Finally, based on the large strain consolidation theory established by Gibson et al. (1981), a new quantitative expression of g(e) considering the initial void ratio and the void ratio at the liquid limit is provided. The influence of the initial void ratio and effective stress on g(e) is discussed.

2 e-σ' relationship considering initial void ratio

Based on Burland’s normalized intrinsic compression curve of remolded clays, Hong et al. (2010) carried out further theoretical and experimental research, and widened the application scope of the intrinsic compression curve. A new concept of remolded yield stress σs′ was proposed by Hong et al. (2010), and σs′ is as follows:

whe re eLis the void ratio at the liquid limit, and e0is the initial void ratio.

In Hong et al. (2010), the intrinsic compression curve was obtained when the effective stress was larger than or equal to the remolded yield stress, but the e-σ′ quantitative expression was not provided when the effective stress was less than the remolded yield stress. Hong et al. (2010) found that the compression curves of remolded soils with different initial void ratios are significantly different when the effective stress is lower than the remolded yield stress. In reclamation projects, the sludge consolidation occurs under the self-weight loading, but the self-weight stress is very small (Sills 1998). Therefore, it is necessary to study the consolidation properties at low stress levels.

Fig. 1 shows the relationship between the void index (Iv) and effective stress for Lianyungang clay at different initial water contents (ω0), which is obtained from the test results of Hong et al. (2010). There is a good linear relationship between the void index and effective stress when the effective stress is less than the remolded yield stress. In order to better reflect this linear relationship, the relationship between the void ratio and effective stress for Baimahu clay is shown in Fig. 2 when σ′ ＜ σs′ . The e-σ′ relationships of Kemen and Lianyungang clays are similar to that of Baimahu clay. Figures dealing with these two are not shown here.

Fig. 1 Relationship between Ivand σ′ for Lianyungang clay at different ω0values

Fig. 2 Relationship between e and σ′ for Baimahu clay at different e0values when σ′ ＜σs′

Further analysis finds that the slope and intercept of the e-σ′ curve have strong correlations with the initial void ratio e0and void ratio at the liquid limit eL. On this basis, the e-σ′ relational expression of Eq. (2) can be provided when the effective stress is less than the remolded yield stress:

Eq. (2) is obtained according to Baimahu clay with the initial void ratios of 1.7, 2.2, 2.4, 3.1, 4.1, and 4.8; Lianyungang clay with the initial void ratios of 1.4, 1.9, 2.1, 2.6, 3.2, and 3.8; and Kemen clay with the initial void ratios of 1.5, 1.9, 2.1, 2.3, 2.4, 2.6, 2.8, and 3.2. Table 1 shows basic physical properties of these clays, from Hong et al. (2010).

Table 1 Basic physical properties of clays

Fig. 3 shows the comparison of the void ratio calculated with Eq. (2) and the measured void ratio for Baimahu and Lianyungang clays. The results indicate that Eq. (2) can well describe the consolidation law while the effective stress is less than the remolded yield stress.

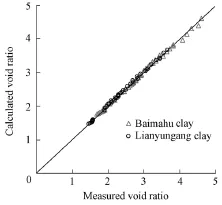
Fig. 3 Comparison of calculated and measured void ratios for Baimahu and Lianyungang clays

When the effective stress is larger than or equal to the remolded yield stress, the e-σ′relationship can be obtained from equations in Hong et al. (2010), as follows:

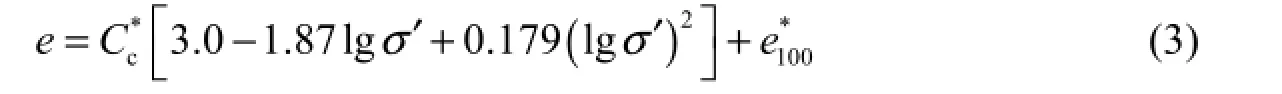
Combining Eqs. (2) and (3), the e-σ′ relationship throughout the consolidation process can be determined as follows:

It is noted that the e-σ′ relationship is established for remolded clays, and the initial water content is 0.7 to 2.0 times the liquid limit. The water content of soils in most reclamation projects is within this range. In the actual project, there may be remolded clays or silts with higher water contents, more than 2.0 times the liquid limit (Deng et al. 2009). Studies have shown that the high water content sludge first enters the deposition process before entering the consolidation process (Been and Sills 1981). After deposition, the water content of sludge is nearly 2.0 times the liquid limit (Ji 2009), which is very close to the values in this study. Thus, the proposed relationship is suitable for most reclamation projects.

3 Nonlinear e-k relationship

Samarasinghe et al. (1982) proposed that the e-k relationship behaved as an exponential expression. Mesri and Olson (1971) described a double logarithmic e-k relationship. However, these established relational expressions were obtained from permeability tests. Nagaraj et al. (1994) only found that the soil permeability coefficient was related to eeLby analyzing the e-k relationship of the remolded soil at the states of normal consolidation and over-consolidation. Then, Eq. (5) was established using permeability data with soil’s liquid limit ranging from 50% to 300% and eeLranging from 0.4 to 1.0.

where kvis the vertical permeability coefficient.

In practical engineering situations, such as those involving reclaimed soil, natural sedimentary soil, and high-sensitivity soil, the soil’s water content is often higher than the liquid limit. In these circumstances, applicability of Eq. (5) needs to be further explored. Therefore, the basic parameters used for establishing e-k equations in Nagaraj et al. (1994), Pane et al. (1983), and Znidarcic et al. (1986) were collected in this study. The liquid limit ranges from 42% to 106%, and eeLis between 0.4 and 2.0. Furthermore, three types of remolded clays, Baimahu clay, Kemen clay, and Huaian clay, were used to establish the e-k relationship in this study. Table 2 shows the soils’ basic properties from previous studies and this study. Based on these data, we obtained the following fitting formula with a correlation coefficient of more than 0.97:

Eq. (6) indicates that there is a strong exponential relationship between eeLand k, as shown in Fig. 4. Fig. 4 shows that Eq. (5) can accurately reflect the e-k relationship while the void ratio ranges from 0.7 to 1.4, but the error is large when it is outside of this range.

Table 2 Soils’ basic properties from previous studies and this study

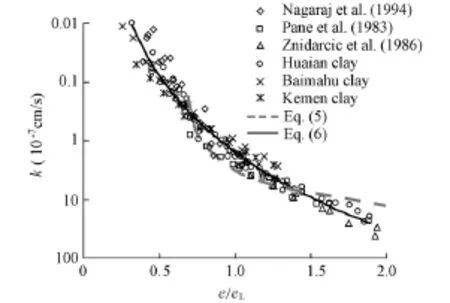
Fig. 4 k vs. e/eL

4 Derivation of g(e) considering initial void ratio

Gibson et al. (1981) established a one-dimensional large strain consolidation equation in the solid phase coordinate according to the balance equation, continuity equation, the principle of effective stress, and Darcy’s law:

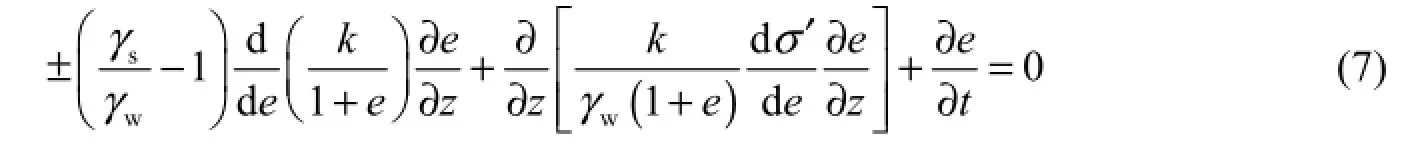
where γwis the specific weight of water, γsis the specific weight of soil particles, z is the solid phase coordinate, and t is time. The symbol + and − are used when the coordinate direction are opposite to and along the gravity direction, respectively.

g(e) defined by Gibson et al. (1981) is as follows:

Substituting Eqs. (4) and (6) into Eq. (8), g(e) as established in the large strain theory can be expressed as

5 Variations of k/(1+e), dσ'/de, and g(e) with σ'

Fig. 5 shows the relationship between k (1 +e) and σ′ for Baimahu clay. As can be seen, k (1 +e) decreases rapidly when the effective stress is less than the remolded yield stress, and then changes slowly as the effective stress increases. The changing law reflects the nonlinear consolidation characteristics. Under a constant effective stress, the value of k (1 +e) increases with the initial void ratio.

Fig. 6 shows the relationship between σ′ and dσ′de calculated with Eq. (4) for Baimahu clay. It can be seen that the change of dσ′de is very small while the effective stressis less than the remolded yield stress. However, when the effective stress is larger than a certain value, dσ′de decreases rapidly. Under a constant effective stress, the larger the initial void ratio is, the larger the value of dσ′de is.

Fig. 5 k (1 +e) vs. σ′ for Baimahu clay

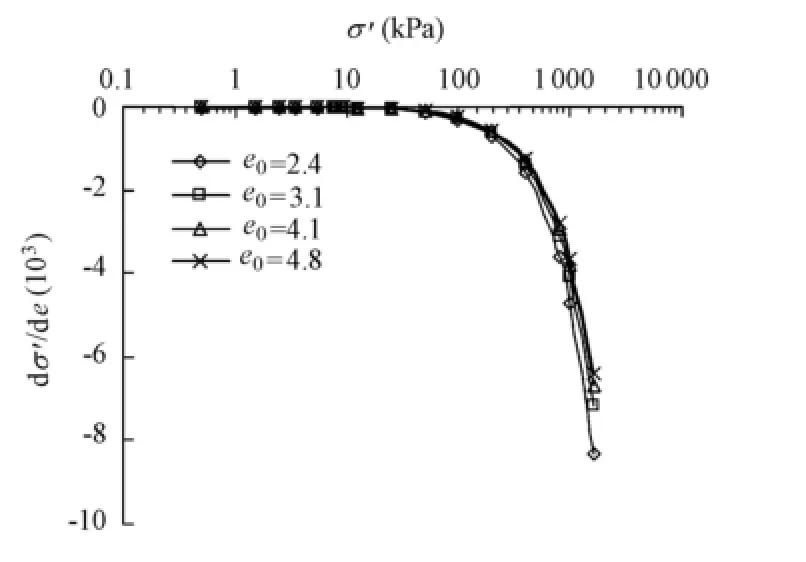
Fig. 6 dσ′de vs. σ′ for Baimahu clay

Fig. 7 shows the relationship between g(e) and σ′, where g(e) is calculated according to Eq. (9). The values of σ′ at the points with the minimum g(e) values are the remolded yield stress of clays corresponding to their initial void ratios. It can be seen that g(e) presents a segmentation change law. When the effective stress is less than the remolded yield stress, g(e) decreases as the effective stress increases, and when the effective stress is larger than the remolded yield stress, g(e) increases rapidly with the effective stress. However, when the effectivestress reaches a certain value, g(e) shows different trends. In Fig. 7(a), g(e) shows a downward trend. In Fig. 7(b), g(e) shows a slower growth trend with small initial void ratios, but shows a downward trend with a relatively high initial void ratio (e0= 3.2). In Fig. 7(c), g(e) grows slower as the effective stress increases.

Fig. 7 g(e) versus σ′ for three remolded clays

The variation of g(e) reflects the dominant position of the permeability and compression coefficients. The turning point under low stress conditions is due to the yield pressure of remolded soil. In the high void ratio stage, the permeability coefficient plays a leading role in the changing process of g(e), and the rapidly decreasing permeability coefficient leads to the decrease of g(e). Yield failure occurs in the soil structure when the effective stress is relatively large, and soil’s compressibility plays a leading role in the change of g(e), so g(e) increases rapidly with compressibility. When the loading is larger, soil particles are more closely arranged. At this stage, the permeability and compressibility of soil gradually stabilize, and the increment speed of g(e) slows down.

On the other hand, when the effective stress is less than the remolded yield stress, the value of g(e) at a high initial void ratio is less than that at a low initial void ratio under a constant effective stress. However, when the effective stress is larger than the remolded yield stress, the change law of g(e) is opposite. This shows that the influence of the initial void ratio on consolidation parameters cannot be ignored.

6 Conclusions

Based on the research of Hong et al. (2010) and Nagaraj et al. (1994), the following conclusions have been reached in this study:

(1) The e-σ′ relationship considering the influence of the initial water content was established, and the relationship differs under the conditions of σ′ ＜ σs′ and σ′ ≥ σs′ .

(2) An extended e-k expression was obtained based on Nagaraj’s equation, which was suitable for dredged sludge with a liquid limit ranging from 44% to 106% and an e/eLvalue between 0.4 and 2.0.

(3) g(e) decreases with the increase of the effective stress when the effective stress is less than the remolded yield stress. However, when the effective stress is larger than the remolded yield stress, g(e) increases rapidly with the effective stress. The variation of g(e) reflects the dominant position of the permeability and compression coefficients.

(4) When the effective stress is less than the remolded yield stress, the value of g(e) at a high initial void ratio is less than that at a low initial void ratio, and the influence of the initial void ratio on consolidation parameters cannot be ignored.

Been, K., and Sills, G. C. 1981. Self-weight consolidation of soft soils: an experimental and theoretical study. Géotechnique, 31(4), 519-535. [doi:10.1680/geot.1981.31.4.519]

Burland, J. B. 1990. On the compressibility and shear strength of natural clays. Géotechnique, 40(3), 329-378. [doi:10.1680/geot.1990.40.3.329]

Carrier, W. D., Bromwell, L. G., and Somogyi, F. 1983. Design capacity of slurried mineral waste ponds. Journal of Geotechnical Engineeing, 109(5), 699-716. [doi:10.1061/(ASCE)0733-9410(1983) 109:5(699)]

Davis, E. H., and Raymond, G. P. 1965. A non-linear theory of consolidation. Géotechnique, 15(2), 161-173. [doi:10.1680/geot.1965.15.2.161]

Deng, D. S., Hong, Z. S., Liu, C. J., Ding, J. W., and Hong, P. Y. 2009. Large-scale model tests on dewater of dredged clay by use of ventilating vacuum method. Chinese Journal of Geotechnical Engineering, 31(2), 250-253. (in Chinese)

Gibson, R. E., Schiffman, R. L., and Cargill, K. W. 1981. The theory of one-dimensional consolidation of saturated clays, Ⅱ: Finite nonlinear consolidation of thick homogeneous layers. Canadian Geotechnical Journal, 18(2), 280-293. [doi:10.1139/t81-030]

Hong, Z. S., Yin, J., and Cui, Y. J. 2010. Compression behaviour of reconstituted soils at high initial water contents. Géotechnique, 60(9), 691-700. [doi:10.1680/geot.09.P.059]

Ji, F. 2009. Deposition Law of Baimahu Dredged Clays and Experiment Study on Dewatering with Ventilating Vacuum Method. Ph. D. Dissertation. Nanjing: Southeast University. (in Chinese)

Jiang, H. H., Liu, G. N., and Zhao, Y. M. 2010. A solution of Gibson’s governing equation of one-dimensional consolidation. Chinese Journal of Geotechnical Engineering, 32(5), 745-750. (in Chinese)

Mesri, G., and Olson, R. E. 1971. Mechanisms controlling the permeability of clays. Clays and Clay Minerals, 19(3), 151-158. [doi:10.1346/CCMN.1971.0190303]

Nagaraj, T. S., Pandian, N. S., and Narasimha, P. S. R. 1994. Stress-state-permeability relations for overconsolidated clays. Géotechnique, 44(2), 333-336. [doi:10.1680/geot.1994.44.2.349]

Pane, V., Croce, P., Znidarcic, D., Ko, H. Y., Olsen, H. W., and Schiffman, R. L. 1983. Effects of consolidation on permeability measurements for soft clay. Géotechnique, 33(1), 67-72. [doi:10.1680/geot.1983.33.1.67] Samarasinghe, A. M., Huang, Y. H., and Drnevich, V. P. 1982. Permeability and consolidation of normally consolidated soils. Journal of the Geotechnical Engineering Division, 108(6), 835-850.

Sills, G. 1998. Development of structure in sedimenting soils. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 356(1747), 2515-2534. [doi:10.1098/ rsta.1998.0284]

Taylor, D.W. 1948. Fundamentals of Soil Mechanics. New York: John Wiley and Sons.

Zhang, J. F. 2002. Study on Analytical Theory of One-dimensional Large Strain Consolidation Problem. Ph. D. Dissertation. Hangzhou: Zhejiang University. (in Chinese)

Znidarcic, D., Schiffman, R. L., Pane, V., Croce, P., Ko, H. Y., and Olsen, H. W. 1986. The theory of one-dimensional consolidation of saturated clays, Part V: Constant rate of deformation testing and analysis. Géotechnique, 36(2), 227-237. [doi:10.1680/geot.1986.36.2.227]

(Edited by Yan LEI)

This work was supported by the Innovation Program for 2011 College Graduates of Jiangsu Province (Grant No. CXZZ_0158) and the National Natural Science Foundation of China (Grant No. 51178107).

*Corresponding author (e-mail: paradise456917@163.com)

Received Dec. 2, 2012; accepted Apr. 2, 2013