两个参数受到随机干扰的一类传染病模型研究∗
曹虹,滕志东
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
为了研究流行病,吴穹和王克[1]引入如下模型:
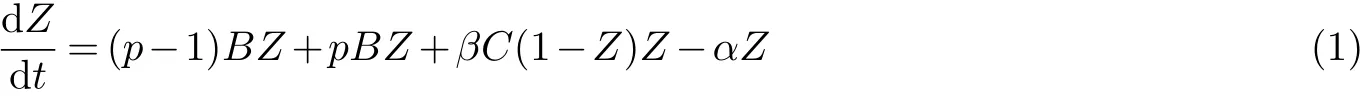

其内禀增长率

作者在[1]中通过考虑传染率β受到随机噪声的干扰,用β0+ρη(t)代替β,ρ表示干扰强度,η(t)表示期望为0,方差为1的Brown运动,(1)就随机化为如下模型:
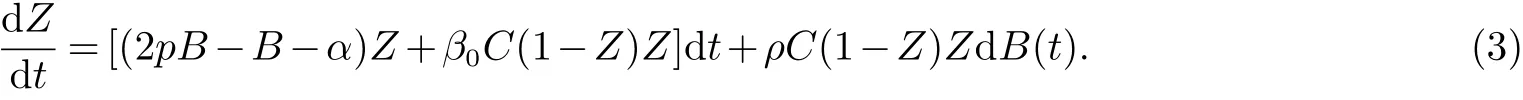
通过使用Fokker-Planck方程方法,作者在[1]中分别详细的讨论了基本再生数1时模型(3)的动力学性质.
可是,在现实世界中,模型中的其他参数也无一不例外的受到环境的随机干扰,不同个体间的接触率当然和许多随机因素有关,如气候、季节、假日等.因此,为了使模型更合理,我们假设不同个体间的接触率C也受到随机干扰,用C0+ρ2η(t)代替C,则模型(3)就随机化为如下模型(4):

其中B1(t),B2(t)是两个独立的Brown运动,ρ1,ρ2表示随机干扰强度,本文主要讨论模型(4)在内禀增长率r=(2p−1)B+β0C0−α大于0,等于0和小于0(即基本再生数分别大于0,等于0和小于0)时的动力学性质,并且得到患病率的期望和方差.
1 全局正解的存在唯一性
定理1设B,β0,α,C0都是正实数,则对任意的初值Z0(0≤Z0<1),存在方程(4)的唯一解Z(t)(t≥0),且Z(t)∈[0,1)a.s..
证明方程(4)满足局部Lipschitz条件,因此对任意的初值Z0(0≤Z0<1),方程(4)存在唯一的局部解Z(t),t∈[0,τe),由文献[2]知系统的边界点1是反射的,所以几乎确定的对任意的初值Z0(0≤Z0<1)有Z(t)<1,而0是方程(4)的解.因此,对任意的初值Z0(0≤Z0<1),方程的解都依概率1保留在区间[0,1)中.证毕.
注1证Z(t)<1,还可用[3]中的方法.
注2证存在性也可用[4]中的方法.
2 Fokker-Planck方程
接下来讨论(4)相应的Fokker-Planck方程,把(4)记为
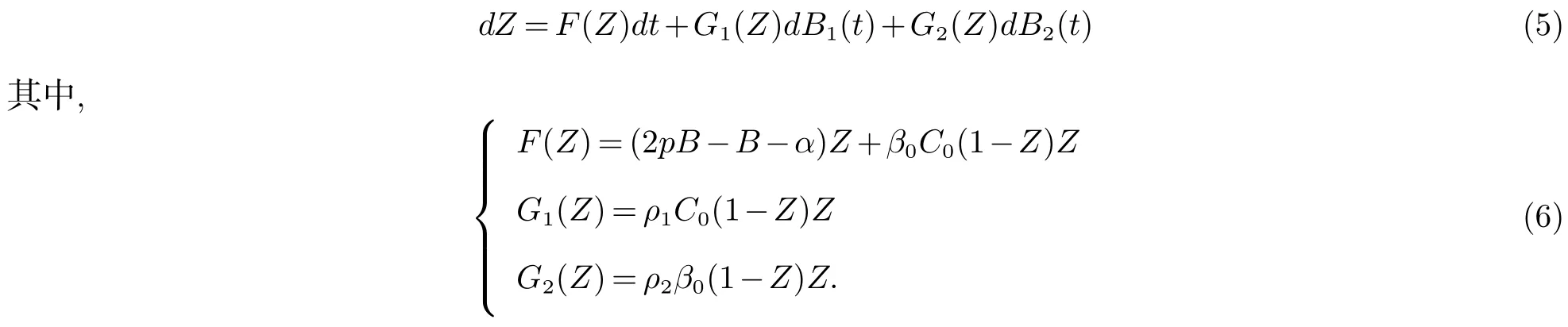
由文献[2]知方程(5)相应的Fokker-Planck方程为:

其中,P(Z,t)表示t时刻Z(t)的概率密度函数,方程(5)的平稳解P∗(Z)满足

则由文献[5]求解P∗(Z),函数P∗(Z)可以表示为


记P∗(Z)的表达式为:


显然,P∗(Z)的临界点是函数T(Z)的零点.
3 模型的动力学性质
3.1 内禀增长率r>0的情况
(1)ρ2
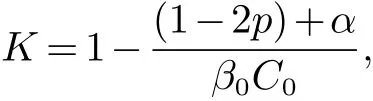
当ρ2→r时,其峰值将趋近于0.这表明,经过一段时间之后,患病率很大(接近1)和患病率很小(接近0)的可能性都不大,患病率以比较大的可能性分布在密度函数P∗(Z)的峰值附近.(如图1,2,ρ=0.05,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627)

图1 当 ρ=0.05,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627 Z ∈[0,1),P∗(Z)的图像

图2 当 ρ=0.05,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627 Z∈[0,0.2],P∗(Z)的图像
(2)ρ2=r时,则(8)变为

求导知P∗(Z)的临界点相应于下面函数的零点

也就是说,P∗(Z)只在处有一个极值点.密度函数P∗(Z)当Z→1−时趋于0,当Z→0+时趋于其图像是单峰的.(如图3,4,ρ=0.057965507,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627)
(3)r<ρ2<2r时,则密度函数P∗(Z)在Z=0处是奇异的.但由2则密度函数P∗(Z)在Z=0是可积的.T(0)=ρ2−r>0,T(1)=(1−2P)B>0.密度函数P∗(Z)的极值点相应于函数(9)的零点.
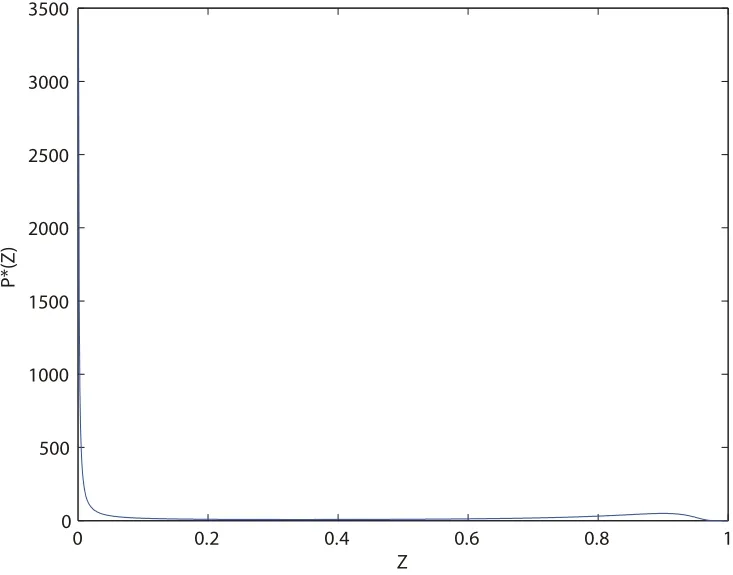
① 当r−3ρ2+(1−2p)B+α≥0时,此时,函数T(Z)在区间0 图3 当ρ=0.057965507,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627,Z∈[0,1),P∗(Z)的图像 图4 当ρ=0.057965507,p=0.35,α=0.03,β0=0.18,B=0.265,C=0.627,Z∈[0,0.1],P∗(Z)的图像 ② 当r−3ρ2+(1−2p)B+α<0时,令∆是函数(9)的判别式. 情形1.∆<0,函数(9)没有零点,于是得到 此时,模型(4)的动力学性质同①. 图5 当 ρ=0.15332,p=0.45,α=0.03,β0=0.19,B=0.465,C=0.627,Z∈[0,1),P∗(Z)的图像 图6 当 ρ=0.476325,p=0.50,α=0.03,β0=0.19,B=0.465,C=0.627,Z ∈[0,1),P∗(Z)的图像 (4)ρ2>2r时,密度函数P∗(Z)在Z=0奇异且不可积的,此时P∗(Z)可表示成为在Z=0处的delta[7,8,9]函数,疾病依概率1趋于消亡.此时,ρ2>2r等价于成立,这表明,随机干扰强度大的可以导致疾病的消亡,而若没有随机干扰,疾病在这种情况下会一直存在下去. (1)(1−2p)B+α>0时,这种情况类似于0≤p≤成立的情况,因而自然有类似的结果.也就是说,若ρ2<2r,P∗(Z)会趋于一个均衡分布.若ρ2≥2r,P∗(Z)是一个趋于0点的delta分布.但还是有一些区别,前者要求时,两者有同样的动力学性质. (2)(1−2p)B+α=0时,由方程(8)知,P∗(Z)在ρ2<2r时在Z=0,1时是奇异的,在Z=0处可积,但在Z=1处不可积.在ρ2>2r时在Z=0,1处是奇异的且不可积的,因而前者P∗(Z)对应于在Z=0处的delta分布,而后者对应于在在Z=0处或在Z=1处的delta分布,究竟是何种结局依赖于初值条件. (3)(1−2p)B+α<0时,容易验证F(Z)>0,于是Z=1成为进入的边界点,由文献[10],Z(t)将依概率1在有限时间内到达Z=1.也就是说,几乎所有的个体最终都要患病.这是一个很糟糕的情况. 接下来,考虑r=2pB+β0C0−B−α=0的情况,此时(6)变为 显然,P∗(Z)可表示成为在Z=0处的delta函数.这表明,随着时间增加,患病率将趋于0,疾病将以概率1趋于消亡. 此时,平稳分布的概率密度函数P∗(Z)满足 显然,P∗(Z)可表示成为在Z=0处的delta函数.这表明,在这种情形下,随着时间增加,患病率将趋于0,疾病将以概率1趋于消亡. 由(7)积分得 由(12)积分和(6)得 由(12)两边乘Z−1再积分得 再由(13)和(14)可得 这样就得到了均值和方差的表达式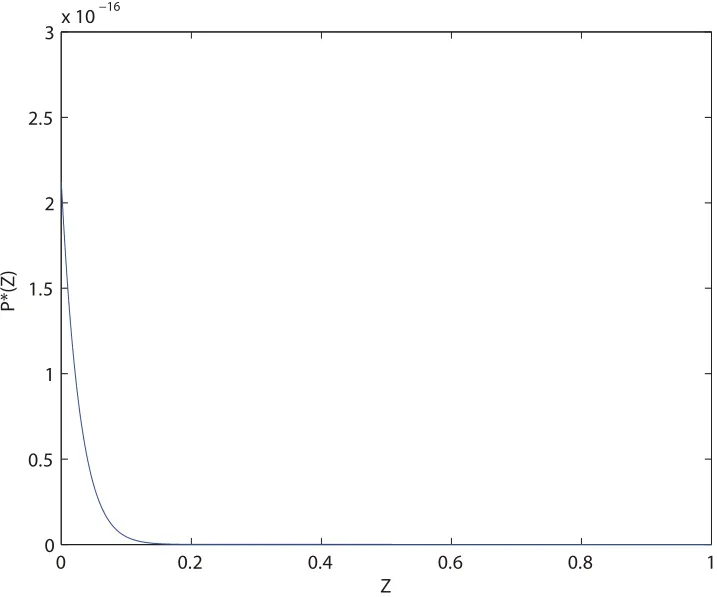



3.2 内禀增长率r=0的情况

3.3 内禀增长率r<0的情况

4 患病率的期望和方差