Global Exponential Stability for Time-varying Delays Cellular Neural Networks with Impulsive Effects∗

YU Zai-zheng,JIANG Hai-jun,HU Cheng

(College of Mathematics and System Sciences,Xinjiang University,Urumqi,Xinjiang 830046,China)

Abstract: In this paper,the problem of exponential stability is investigated for cellular neural networks with timevarying delays and impulsive Effect.By using the Lyapunov functional method and applying Young inequality,some sufficient conditions are derived to ensure the exponential stability of the neural networks.An example is given to show the Effectiveness of the presented criteria.

Key words:exponential stability,impulsive cellular neural network,time-varying delay,lyapunov function

0 Introduction

Nowadays,cellular neural networks(CNNs),introduced by Chua and Yang in 1988[1,2],have been successfully applied to signal processing,image processing,solving nonlinear algebraic and transcendental equations and some classes of optimisation problems.Some of these applications require that the designed CNNs are stable.In the implementation of artificial neural networks,time delays are unavoidable due tofinite switching speeds of the amplifiers.These lead to the model of CNNs with delay(DCNNs)[3∼6].Hence,the stability of DCNNs is an important problem in theory and applications.

On the other hand,many evolutionary processes in applied areas such as biological systems,bursting rhythm models in pathology and frequency-modulated signal processing systems undergo abrupt changes of states at certain time instants.As artificial electronic systems,neural networks are often subject to impulsive perturbation,which can affect the dynamical behaviors of neural network systems[8∼10].Therefore,it is of practical importance to study the impulsive Effects on the stability property of neural networks.

Since delays and impulses can affect the dynamical behaviors of the system,a neural network model with delay and impulsive Effects should be more accurate to describe the evolutionary process of the systems,and it is necessary to investigate both delay and impulsive Effects on the stability of neural networks[11∼13].

Currently,a large number of the criteria on the stability of DCNNs without impulse has been derived.However,there is not much work dedicated to investigating the stability of impulsive neural networks.In this paper,we formulate a neural network model with time-varying delays and impulsive Effects.And then,some new and useful criteria of the globally exponential stability are deprived based on p-norm and∞-norm by Young inequality,Lyapunov functional method and analysis method.A numerical example is given to demonstrate the Effectiveness of the obtained results.

1 Problem formulation and some preliminaries

We consider the following impulsive CNNs with time-varying delays

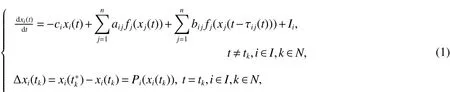
where i∈I={1,2,...,n},n corresponds to the number of units in a neural network,xi(t)is the state variable of the ith neuron at time t;fj(xj(t))denotes the output of the jth unit at time t;Further,aij,bij,Ii,ciare constants,aijdenotes the strength of the jth unit on the ith unit at time t;bijdenotes the strength of the jth unit on the ith unit at time t−τij(t);Iidenotes the external bias on the ith unit;τij(t)corresponds to the transmission delay along the axon of the jth unit from the ith unit and satisfies 0 ≤ τij(t)≤ τ(τ is a constant);cirepresents the rate with which the ith unit will reset its potential to the resting state in isolation when disconnect from the network and external inputs.{tk|k=1,2,...}satisfies∈[R,R]represents the abrupt change of the state xi(t)at the moment tk.

System(1)is supplemented with initial value given by

where φ(s)=(φ1(s),φ2(s),...,φn(s))T∈ C([−τ,0],Rn),which denotes the Banach space of all continuous functions mapping[−τ,0]into Rn.

In this paper,for systems(1),we introduce the following assumptions.(H1)For all x,y∈R,there exist positive constant Mi,such that

(H3)inft∈R+,in whichτij(t)(i,j=1,2,...,n)denotes the derivative of τij(t).

Definition 1The following two norms are used throughout the paper.

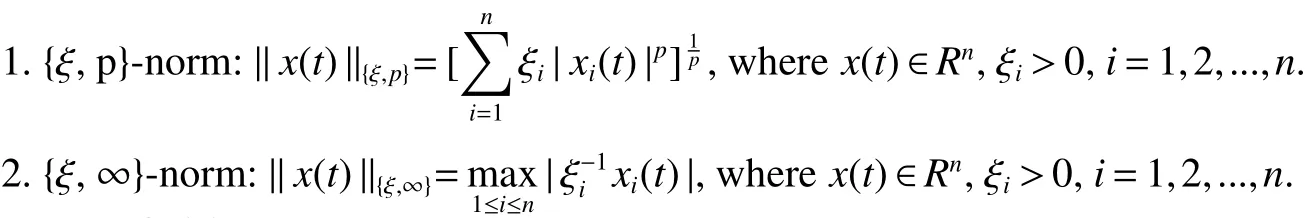
Definition 2For any φ ∈ C([−τ,0],Rn),define the following norms:

Definition 3Assume that x(t)and y(t)are any two solutions of system(1)with different initial values φ,ϕ ∈C([−τ,0],Rn).If there exist constants G ≥1 and ε>0,such that

Then system(1)is said to be globally exponentially stable.

Definition 4Let f(t):R→R be a continuous function,then the Dini right derivative of f(t)is defined as

From Definition 3,we can easily obtain the following lemma:

Lemma 1[6]Let f(t):R→R be a continuous function,if f(t)is differentiable at t0,then

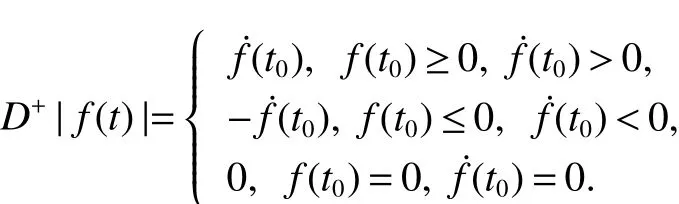
Next we give Young inequality,it plays a key role in the proof of the main results.

Lemma 2[7,14]Let a>0,b>0,p>1,q>1 and=1.Then we have the inequality

2 Main results

In this section,we investigate the globally exponential stability of system(1).

Theorem 1Suppose(H1)and(H2)hold and there are positive constants ξ1,ξ2,...,ξnand α>0,such that

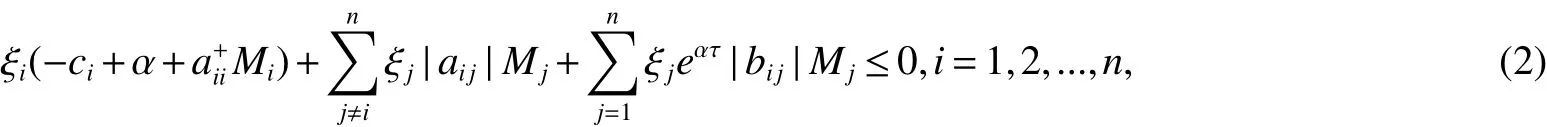
ProofLet u(t)=eαt[x(t)−y(t)],then

According to(H1),we obtain

According to Definition 1,there is an i0=i0(t),which depends on t,such that

Furthermore,let

By Eq.(7)and(8),we have

It shows that ku(t)k{ξ,∞}is decreasing and bounded for t>0,andthat is

When t=tk,by(H3),

From(10)and(11),ku(t)k{ξ,∞}is decreasing monotone for any t≥ 0,we obtain

which means that system(1)is globally exponentially stable.The proof is complete.

Corollary 1Suppose(H1)and(H2)hold and there are positive constants ξ1,ξ2,...,ξn,such that

Evidently,ifcondition(14)holds,thenwecanfindaconstantαsuchthatcondition(2)holds.Therefore,Corollary 1 is a direct consequence of Theorem 1.

Theorem 2Suppose(H1)−(H3)hold,for any t≥ 0,if there are positive constants ξ1,ξ2,...,ξn,α >0,and αij,βij∈R,such that

ProofLet u(t)=eαt[x(t)−y(t)],then

Define a Lyapunov functional as follows:

By using Young inequality,we can derive that

It shows that

When t=tk,by(H3),

Then

From(22)and(23),V(t)is decreasing monotone for any t≥0,we obtain

for any t≥0,where

which means system(1)is globally exponentially stable.Theorem 2 is proved completely.

Corollary 2Suppose(H1)−(H3)hold,for any t≥ 0,if there are positive constants ξ1,ξ2,...,ξn,and αij,βij∈ R,such that

Evidently,if condition(26)holds,then we canfind a constant α such that condition(15)holds.Therefore,Corollary 2 is a direct consequence of Theorem 2.

3 An illustrative example

In this section,we give an example to illustrate the Effectiveness of the results obtained in the previous section.

ExampleConsider the impulsive neural differential equation with time-varying delays

where n=2,I1=I2=1,c1=c2=4

Taking p=2,αij=βij=1,ξj=1,α=1,γik=−1.

Under the assumption of the example,by easily calculating,condition(15)holds,then by Theorem 2,system(27)is globally exponentially stable.

4 Conclusions

In this paper,we considered the exponential stability for a class of delayed neural networks with impulses.Some new and useful criteria of the globally exponential stability are derived based on p-norm and∞-norm by Young inequality,Lyapunov functional method and analysis method.It is worthwhile to mention that our technical methods are practical,in the sense that all new stability conditions are stated is simple algebraic forms,so their verification and applications are straightforward and convenient.Finally,an example is given to illustrate the Effectiveness of the proposed results.