环形铁心型有限转角电动机的电枢反应分析

袁永杰，李立娜，王佳鹂，冯 旭，严 亮

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

目前，连续旋转的直流电动机已得到了广泛的应用，但在一些特殊使用场合，如红外成象、激光标识、激光雷达、光机扫瞄等系统却需要一种只作往复摆动、体积小、精度高、寿命长、可靠性高的直流电动机。在这些特殊系统中，普通有刷直流电动机由于需要电刷和换向器，不但结构复杂而且可靠性不高，另外频繁的往复摆动会造成电刷剧烈跳动，使得和换向器接触不良，对系统造成失踪脉冲，噪声冲击甚至导致系统振荡［1］。无刷直流电动机使用电子换向取代了电刷和换向器的机械换向装置，具有与有刷直流电动机相同的线性调节特性，并且可靠性高，但其控制系统需对电子换向进行信号处理，控制复杂，所需开关管数量较多，成本较高，且转矩波动较大。这种情况下有限转角电动机凸现了它的优势。本文对环形铁心型有限转角电动机进行了电磁仿真分析和电枢反应分析，并通过样机进行了试验验证。

1 基本结构及原理

环形铁心型有限转角电动机电枢(定子)为环形铁心，在其上均匀绕制多匝线圈，转子由永磁体和磁轭组成，如图1所示。

图1 有限转角电动机原理图

环形铁心型有限转角电动机的工作原理与普通永磁直流电动机相同，即通电绕组在磁钢形成的磁场内受力旋转。为保证产生连续同向的力，在规定旋转区域内，使电枢绕组中通过的电流方向相同，由于绕组排布的原因，同向绕组仅在有限区域内，因此其转子转动范围有限。另外，由于该电机是转子磁钢为运动部件，其受力方向与绕组方向相反。环形铁心型有限转角电动机的堵转转矩计算与连续旋转的有刷直流电动机公式完全相同［2］，如下:

式中:T为电磁转矩;p为极对数;a为并联支路对数;I为绕组电流;N为绕组匝数;φ为电机主磁通。

根据该原理设计了一款环形铁心有限转角电动机，其结构图如图2所示。它由机壳、环形铁心和绕组(电枢)、转子磁轭和磁钢(转子)、轴承等零部件组成，结构简单紧凑，可靠性高。

图2 环形铁心型有限转角电动机结构图

样机性能参数如表1所示。

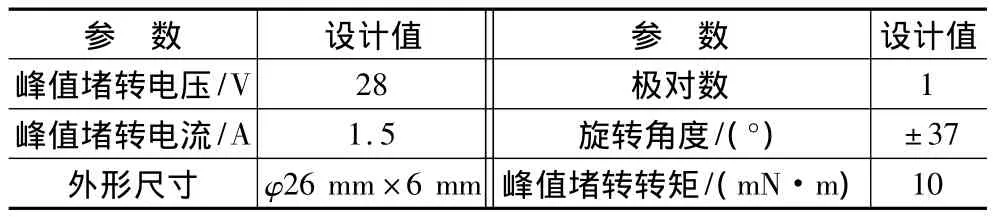
表1 样机性能参数

2 环形铁心型有限转角电动机电枢反应理论分析

环形铁心型有限转角电动机的总磁通由转子磁通和电枢磁通两部分组成，通过有限元建模仿真，其转子磁力线和定转子合成磁力线分别如图3和图4所示。从图3中可以看出，当电枢绕组中没有电流时，即不存在电枢磁场的情况下，转子磁场均匀分布。当电枢绕组中通电产生电枢磁场时，电枢磁场对转子磁场产生了影响，即电枢反应，使得气隙磁密为零的位置发生了偏移，如图4所示。

图3 转子磁场磁力线

图4 合成磁场磁力线

图5 等效磁路图

根据环形绕线型有限转角电动机的基本结构和磁路走向，画出等效磁路图，如图5所示。其中θ为转子磁钢方向与+X轴的夹角，FS为电枢半周磁势，FR为转子磁钢磁势，Rδ为气隙磁阻，RS为半周电枢磁阻，RR为转子磁阻，φ为电机主磁通，φm1和φm2为回路磁通。

根据克希荷夫定律，按照图示参考方向，列出磁路方程:

整理得到气隙总磁通φ:

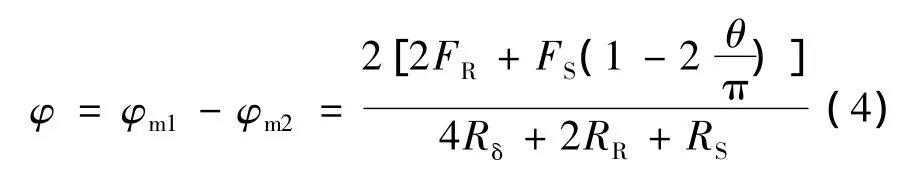
从式(4)可以看出，随着转子位置的变化，即θ变化，总磁通发生变化，转矩亦随之改变。

4)电机总磁通的变化量与电枢磁势相关，在转子磁势一定的情况下，电枢磁势越大，主磁通的变化量就越大，转矩波动越大。

由以上分析可知，在电机运转过程中，由于电枢反应的原因，随着转子位置的变化，电机总磁通是在逐渐变化的，其反电势和转矩同样随之改变，即产生了转矩波动。

3 电磁仿真分析

本文应用ANSYS公司的Maxwell 2D有限元电磁仿真软件对环形绕线型有限转角电动机进行了空载和负载两种情况下的仿真分析。有限元模型如图6所示，最外层为空气，边界条件采用了气球边界。设置转子以恒定的转速旋转，电机空载反电势如图7所示。当绕组中没有电流时，即不存在电枢反应时，反电势在规定范围内为恒定值。

图6 有限元仿真模型

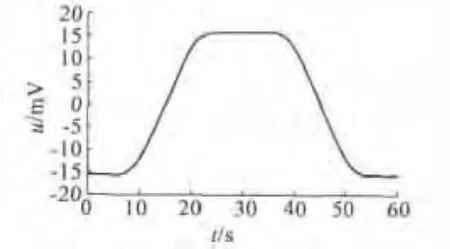
图7 电机空载反电势

电机绕组通恒定电流时，电机负载反电势如图8所示，获得电机负载转矩如图9所示。

图8 电机负载反电势

图9 电机负载转矩

从图中可以看出，负载情况下，即当电机电枢绕组内通电流时，随着转子位置的改变，电机转矩和反电势随之变化，在规定的有限范围内转矩波动达4.2%，即电枢反应引起了电机转矩的变化。

4 试验验证

目前对于转矩波动的测试方法有反电势法和堵转转矩法两种。其中反电势法是用转台以恒定的转速拖动电机，测量电机输出端的反电势，以此来反映转矩波动的情况。该测试方法没有考虑到电枢反应对电机转矩波动的影响，仅相当于电机空载反电势，仅可以作为检测电机绕线排布是否均匀、气隙是否均匀等，而不能真实反映出电枢反应对电机的转矩波动的影响。用该方法测试的样机反电势波形如图10所示。

堵转转矩法是给电机绕组通以恒定电流，在不同位置下对电机进行堵转，测试出堵转转矩，再进行转矩波动的计算。该方法综合考虑了环形铁心有限转角电动机电枢反应的影响，一个方向的测试结果如图11所示。

图10 样机实测反电势波形

图11 实测电机转矩随位置变化情况

由于测试条件的限制，测试点为非极限位置，如图11所示，转矩波动约为2.7%。经计算可知在规定范围内可达3.5%。转矩波动与仿真分析接近，从图中也可以看出电机转矩随位置变化的趋势。

环形铁心型有限转角电动机电枢反应引起的转矩波动是由该类型电机的工作原理和结构决定的，是该类型电机的固有特性。即只要存在电枢反应，就会存在转矩波动，其转矩波动的大小与电枢磁势和定子磁势相关，电枢磁势相对于转子磁势越大，其转矩波动就越大。

5 结 语

通过对环形铁心型有限转角电动机的磁路分析发现，由于电枢反应的影响，随着转子在规定范围内旋转，电机的总磁通是在逐渐变化的。当转子运动到转子磁场和电枢磁场正交时，即电枢磁场为交轴磁场，在不考虑磁路饱和情况下，电枢磁场对总磁通没有影响。在其它位置，电枢磁场对转子磁场起到增磁或去磁作用，总磁通产生变化，电机反电势和转矩随之改变。

环形铁心型有限转角电动机只要存在电枢反应，就会引起转矩波动。因此若需降低转矩波动，可以通过减小定子磁势，增大转子磁势，以此来减小电枢反应的影响。

［1］何松波.有限转角电机［J］.微特电机，1976，4(3):16 －31.

［2］曹春，杨素香，黄宇峰，等.有限转角电动机介绍及主要公式推导［J］.微特电机，2008，36(5):16 －17.

［3］汤蕴璆.电机学［M］.北京:机械工业出版社，2002.