基于电压脉冲矢量法的面装式永磁同步电动机初始位置辨识

王 军，李盛兵，安 芳，王晓嘉

(中国电子科技集团公司第二十一研究所，上海 200233)

0 引 言

近年来，永磁同步电动机作为一种高性能的可调速电机在工业领域中的应用日趋广泛，其凭借高效率、高功率密度、高可靠性以及较长的使用寿命等优点，在某些领域正逐步取代传统的气动、液压驱动和异步电动机驱动。由于永磁同步电动机的转子采用的是永磁体，所以想要正常驱动电机就需要获取转子的绝对位置。常用的获取转子绝对位置的方式是通过在电机轴部安装的编码器或旋转变压器，但安装位置传感器会提高电机驱动器的成本，增大电机的体积，降低设备的可靠性，所以许多科研工作者在无位置传感器电机的控制方面做了大量的研究，如文献［1－3］。常见的无传感器控制策略大多基于电机反电动势，该方法对于参数变化较为敏感，此外还有一个比较重要的缺陷是低速和零速时，反电动势信号很容易淹没在噪声信号中或是根本没有反电动势信号，这就对电机起动造成了一定的影响，当负载较大时，很容易由于失步造成起动失败等现象。所以，如何能较好地辨识出转子的初始位置，对于永磁同步电动机的无传感器控制的性能与应用范围至关重要。

在永磁同步电动机转子初始位置辨识方面，比较有代表性的方法有转子预定位法［4］，旋转高频信号注入法［5］和电压脉冲矢量法［6］。转子预定位法是通过向定子绕组中注入电流的方式，使其预先转到固定的角度，再从该角度处开始进行驱动控制。该方法的优点是控制算法简单，但由于电机的初始角度是随机的，注入的电流会使电机发生不可预测的正反转，这就限制了该方法的应用范围，使其大多只能应用在风机、压缩机、水泵等对电机初始定位运动不是很敏感的场合。旋转高频信号注入法是向电机绕组中注入旋转的高频电压矢量，通过对高频电流响应信号进行滤波和拟合获得转子的初始位置，再利用定子铁心的磁路饱和差异进一步判断永磁体N/S极位置。该算法理论上可获得较高的检测精度，但由于算法中涉及到数字滤波器和拟合处理，导致实际应用较难实现且效果一般。电压脉冲矢量法利用永磁同步电动机的结构性凸极或是饱和凸极效应，向电机绕组中通入一系列的电压脉冲矢量，通过比较电流响应的幅值并对采样电流进行运算来获取转子的位置。该算法在检测初始位置过程中电机不会发生明显的运动，检测精度较高，算法易于实现。本文采用电压脉冲矢量对永磁同步电动机的初始角度进行辨识，并改进了传统的矢量注入方式，优化辨识算法，使其辨识效果得到改善且更加易于工程实现。

1 理论分析

永磁同步电动机理论上都具有一定的凸极特性，只不过插入式与内装式永磁同步电动机由于具有结构性凸极，凸极效应较为明显，而面装式永磁同步电动机在磁路饱和情况下也会具有一定的凸极特性。本文所研究的对象为面装式永磁同步电动机，如图1所示。它在dq坐标系中的磁链方程如下:

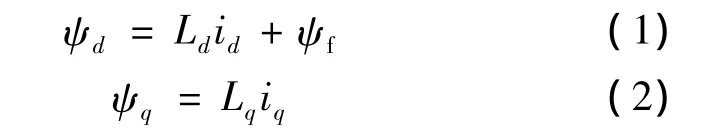
由于永磁同步电动机在d轴上存在着永磁体产生的磁场ψf，它与电枢磁场相互作用，就会增强或削弱d轴的磁路饱和程度。

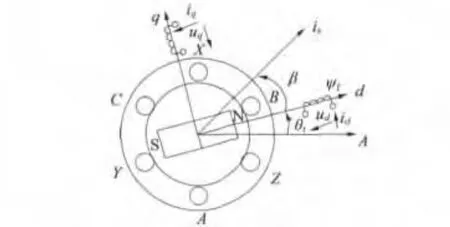
图1 面装式永磁同步电动机示意图

将磁链方程中的电感划分为励磁电感和漏感，式(1)可以改写:

式中:Lmd为d轴主磁路励磁电感;Lsσ为dq线圈的漏感;if为等效励磁电流。对于d轴主磁路励磁磁场，则有:

由式(4)和图2可知，当直轴电流id与if方向一致时，会使d轴主磁路趋向饱和，Lmd降低，反之则会使主磁路的饱和程度降低，Lmd升高，这也就是所谓的饱和凸极效应。所以，可以认为主磁路的饱和程度与id的大小和方向密切相关，同理也与定子电流矢量is与ψf的夹角β及其幅值密切相关［7］。

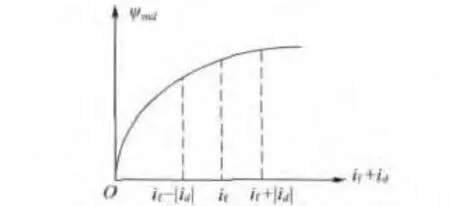
图2 d轴主磁路磁化曲线

若仅考虑A相绕组，从图1中我们可以看到，当θr为0°时，A相绕组产生的磁链ψmA与d轴重合，也就是与永磁体的磁链ψf重合，A轴磁路饱和程度最高，励磁电感值LmA最小;当θr为90°时，A相绕组产生的磁链ψmA与永磁体的磁链ψf垂直，不影响A轴磁路，励磁电感值 LmA不受电枢反应影响;当 θr为180°时，A相绕组产生的磁链ψmA与永磁体的磁链ψf方向相反，A轴磁路饱和程度最低，励磁电感值LmA最大。对于B相与C相绕组，情况相似，区别在于θr要有120°的偏置。假设绕组的励磁电感值以转子角度为变量服从正弦规律变化，我们便可以利用电感值估算转子位置了。但实际应用中，电感值不易直接测量，考虑到当绕组中注入的是高频电压脉冲时，定子绕组中产生的电流峰值与绕组中的等效电感呈反比关系，而绕组电流又是电机控制中的常用反馈信号，于是我们可以通过测量绕组中的电流峰值来估算转子的位置。

2 初始位置辨识策略

假设绕组中的电流峰值ipeak与该相绕组转子磁链ψf的夹角θr有如下数学关系式［8］:

式中:iav为电流峰值的平均值;ipeak－max为电流峰值的最大值;ipeak－min为电流峰值的最小值。

为了得到绕组磁链 ψmA，ψmB，ψmC，本文依据电压空间矢量原理选择了六个电压矢量，如图3所示。通过这六个电压脉冲矢量，我们可以得到其对应的电流峰值响应:

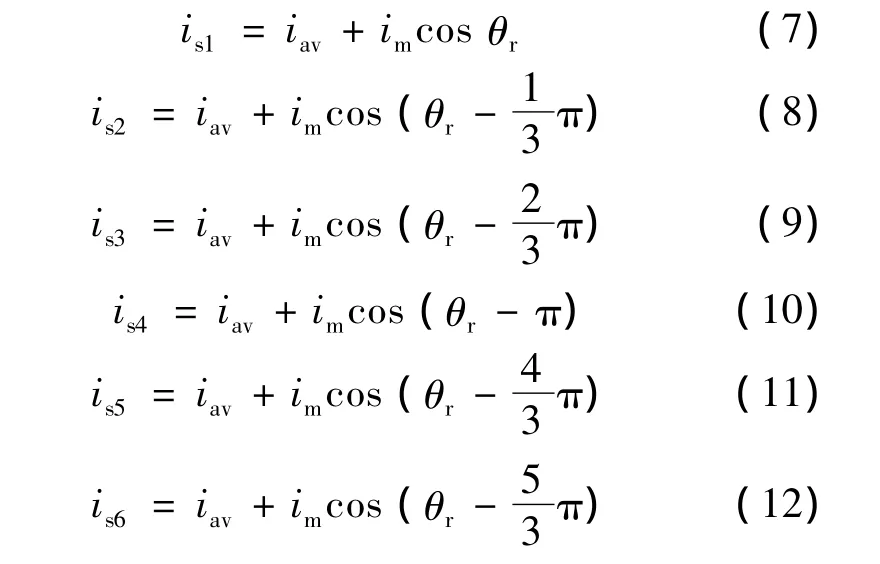
由于式(8)、式(10)、式(12)与式(11)、式(7)、式(9)为同一绕组上方向相反的脉冲矢量的电流峰值响应，于是我们可以得到A，B，C三相绕组电流峰值的差值与转子角度的关系式:

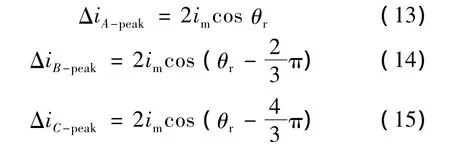
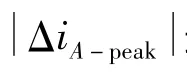
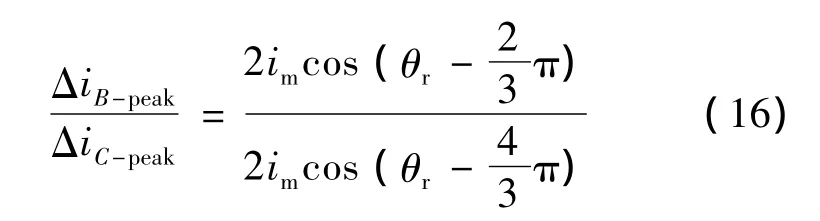
整理化简后我们得到:

由式(17)可知，通过求反正切的方式可以得到估算的转子位置，式(18)中，θsection为估算角度偏置角。

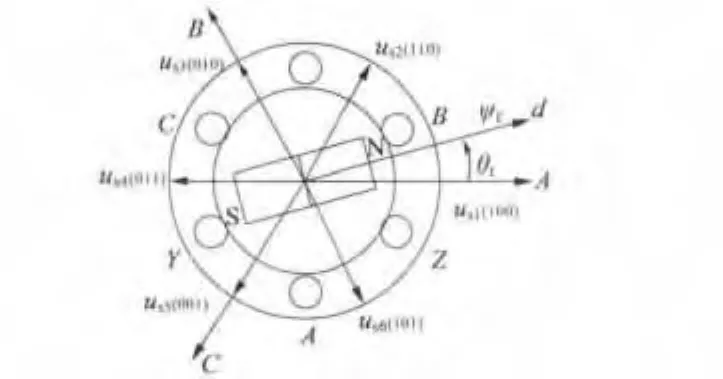
图3 电压空间矢量示意图

基于电压脉冲矢量法的转子初始位置辨识算法的流程图如图4所示。首先向电机三相绕组中注入六路高频电压脉冲矢量并采样得到相电流峰值。这一环节比较关键，测量ipeak－max时，在施加相应绕组的正向脉冲矢量后需要紧接着施加该绕组的负向脉冲，以使绕组中的电流恢复为零，并且电流波形较为对称，如图5所示，同理测量ipeak－min时也需要进行该处理。考虑到电机的剩磁和磁滞效应可能会对电机的饱和特性造成影响，可以采用多次注入同一个电压脉冲矢量对的方式来削弱这一影响，并且为了获得正确的采样结果，还应该保持这些脉冲矢量对的连续性。此外，脉冲矢量的模值和持续时间也是比较重要的参数，如果脉冲矢量的模值过大，持续时间太长，会造成电机出现较为明显的抖动;如果模值较小，持续时间过短，则电机的饱和性凸极效果可能不够明显，影响角度估计精度。因此，可能需要进行多次试验与调整才能得到一组较为合适的参数。采样得到电流峰值后，我们就可以通过将正向脉冲矢量对应的电流峰值的绝对值减去负向脉冲矢量对应的电流的峰值的绝对值得到该相电流峰值的变化量。其中，电流峰值变化量的绝对值最大的一相就是电机的转子磁极最靠近的那相绕组。利用剩余两相的电流峰值的变化量，根据式(18)便可得到估算出的转子初始位置。

图4 永磁同步电动机转子初始位置辨识算法流程图

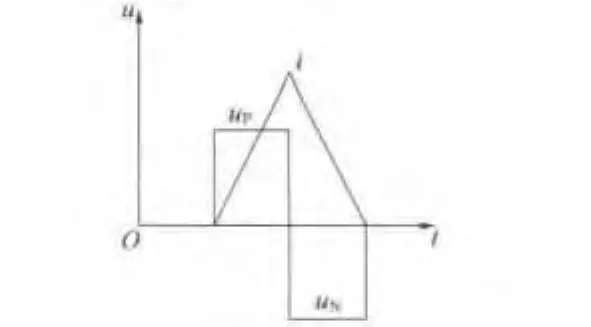
图5 电压脉冲矢量注入方式

该辨识算法中的一个重要环节是电压脉冲矢量的生成，传统的获得电压脉冲矢量的方式是通过向电机绕组中通入不同方向的电流实现的，如文献［8］。由于本文采用的控制系统中包含SVPWM模块，所以利用该模块来生成电压脉冲矢量比直接向绕组中注入电流更加简便易行，两种方式的对比如表1所示。

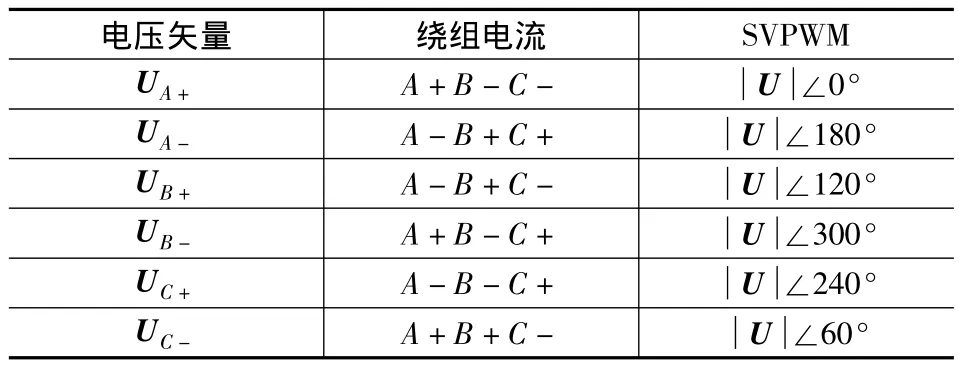
表1 电压矢量生成方式对比

整个控制系统的核心部分原理框图如图6所示。本文在不打乱原有控制系统结构的基础上，通过引入开关变量的方式，完成了电机转子初始角度的辨识功能模块的融入。当开关变量如图6中所示状态时，驱动器正在进行转子初始角度辨识。此状态下，电压给定，角度反馈和电流反馈均从正常控制环路中断开。这样，我们就可以通过选取特定的值作为矢量的模值，分别令 θ*等于 0°、60°、120°、180°、240°、300°来生成六路电压矢量，最后通过对电流采样数据进行处理运算得到转子的初始位置。当转子初始角度辨识完毕后，便可通过开关变量重新将控制环路闭合，以使控制器切换到正常工作模式。可见，该辨识策略在便于实现的同时，保留了原有控制模块的完整性，具有实际的工程应用价值。

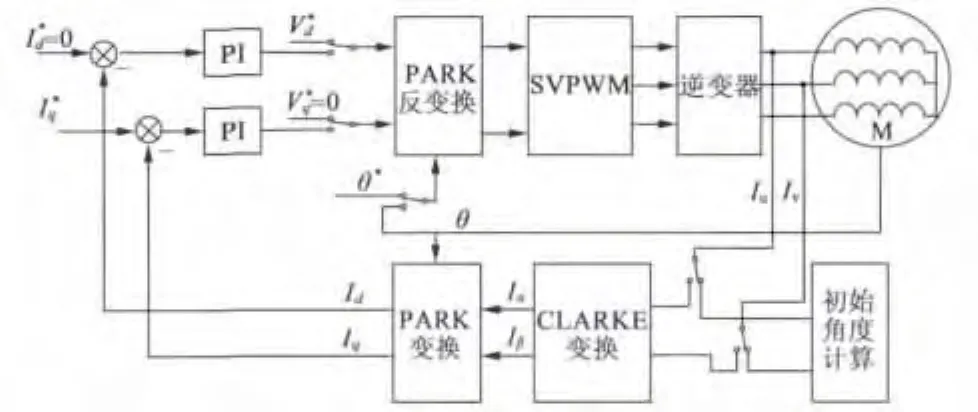
图6 控制系统原理框图

3 实验结果分析

本文的实验平台如图7所示。实验对象为一台750 W面装式四对极永磁同步电动机，额定电流为4.6 A，额定转速为3000 r/min。驱动单元的核心处理器采用的是 Microsemi公司的 SmartFusion，其为ARM和FPGA的混合体，将ARM在控制方面的长处与FPGA并行计算能力强的优点相结合，是SoC较为理想的解决方案。本控制系统的逻辑处理部分由FPGA完成，而包括转子初始位置辨识算法在内的大部分控制算法则是在ARM核中实现的。

图7 实验平台

由图4可知，我们只需向电机中注入六路高频脉冲矢量，采样获得各相电流的正负峰值，便可计算估计出转子的位置。为了检测该位置估计算法的使用效果，故将电机的机械角度以10°为间距取36个采样点。通过获取该采样点的采样电流来估算转子位置，并与实际编码器角度反馈进行比较，以评价该算法的有效性。

对应一个机械周期的36个采样点，得到的电流峰值波形如图8所示。图8表明了面装式永磁同步电动机确实存在着饱和凸极效应，三相峰值电流也随着转子位置的不同而发生变化。由图9和图10，我们可以从直观上评价该位置估计算法的有效性。为了便于直观地观察位置辨识的准确程度，我们画出辨识角度对应的极坐标图，取极径为单位长度，即ρ=1，极角为辨识得到的角度θ，如图9所示，图中的36个点分布越均匀，位置辨识效果越好。图10为位置辨识误差，其中，最大的辨识误差出现在第34 个点，为7.35°，位置辨识的平均误差为3.4°。对于装有增量式编码器的永磁同步电动机，初始位置角度一般是由霍尔信号得到的，相对于转子的实际位置，误差范围为±30°。因此，该转子初始位置估计算法的估计精度完全满足电机起动需要，只要根据辨识出的转子角度选择合适的矢量，一定可以实现永磁同步电动机的大力矩无失步起动。

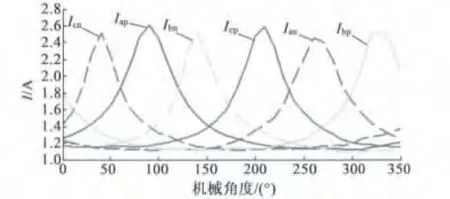
图8 六路电压脉冲矢量对应的相电流峰值

图9 永磁同步电动机转子位置估计

图10 永磁同步电动机转子位置估计误差

4 结 语

本文介绍了一种应用于面装式永磁同步电动机的转子初始位置辨识方法。该方法通过向电机三相绕组中注入六路高频电压脉冲矢量，利用电机的饱和性凸极效应来获取当前转子的位置，具有辨识速度快、精度高、辨识过程电机抖动较小、算法易于实现等优点。而且，由于该辨识方法不依赖于电机参数，因此鲁棒性较强，非常适用于面装式永磁同步电动机无传感器控制时电机的起动。考虑到脉冲矢量的模值和作用时间的选取会影响到辨识过程中电机的抖动以及最终的辨识效果，因此在实际应用中工程人员还需要根据不同的电机与驱动器通过实验的方式来获取最优的参数。

［1］KIM J S，SUL S K.A high performance PMSM drive without rotational position sensors using reduced order observer［C］//Proc.of IEEE －IAS Annual Meeting.1995:75－82.

［2］谷善茂，何凤有，谭国俊.扩展卡尔曼滤波的无传感器低速性能研究［J］.电气传动，2009，39(12):12 －18.

［3］MATSUI N.Sensorless PM brushless DC motor drives［J］.IEEE Trans.on Industrial Electronics，1996，43(2):300 －308.

［4］朱熀秋，成秋良.无起动绕组永磁同步电机初始定位及起动策略［J］.中国电机工程学报，2008，28(9):61－65.

［5］王冉珺，刘恩海.永磁同步电机转子初始位置的检测方法［J］.电机与控制学报，2012，16(1):62 －66.

［6］王子辉，陆凯元，叶云岳.基于改进的脉冲电压注入永磁同步电机转子初始位置检测方法［J］.中国电机工程学报，2011，31(36):95－101.

［7］王成元，夏加宽，杨俊友.电机现代控制技术［M］.西安:机械工业出版社，2008:281－282.

［8］SCHMIDT P B，GASPERI M L，RAY G.Initial rotor angle detection Of a non－salient pole permanent magnet synchronous machine［C］//IEEE Industry Applications Society Annual Meeting.1997:459－463.