永磁直线同步电动机推力波动分析及抑制方法综述

于立娟，秦 平，李登举，王相龙

(吉林大学，长春 130025)

0 引 言

细微进给加工、高速加工都是机械制造及科学研究的重要发展方向。这就要求进给系统具备较高的运动精度、位移刚度以及较大的推力。永磁直线同步电机(以下简称PMLSM)是一种能把电能直接转换成为运动机械能的直线运动装置，PMLSM具有高速、响应快、精度高、推力大等传统“滚珠丝杠+旋转电机”无法比拟的优势。但是由于PMLSM驱动系统中，负载扰动、齿槽力和粘滞摩擦系数变化等诸多原因，推力波动的产生是不可避免的，其中端部效应的影响尤为明显，这一系列问题都将严重恶化伺服系统性能。除此之外，推力波动还能导致在精密数控机床上加工的产品表面出现划痕，这样不但会降低产品质量，严重时直接产生废品［1］。基于上述原因，提高PMLSM的驱动性能，抑制其推力波动已然成为当今日益重要的研究方向。

1 推力波动产生的原因

PMLSM作业过程中，其推力波动严重影响其伺服精度。引起其运动不平稳的原因很多，有外部干扰，如负载、温度及摩擦力的扰动;也有直线电动机系统内部问题，如结构上铁芯两端开断等和运行中产生的干扰谐波等诸多原因。

1.1 系统外部成因

1.1.1 负载阻力变化

PMLSM的工作特点是克服负载阻力来带动工作台做直线运动，然而在电动机运行过程中，负载阻力又是在不断变化的，变化的负载阻力打破了原系统的力平衡，从而引起直线电动机速度出现波动，导致伺服系统性能下降。外部负载的变化可以根据PMLSM工作时负载变化进行预测控制。

1.1.2 摩擦扰动

摩擦扰动主要表现在粘滞摩擦力扰动和滑动摩擦力扰动两方面。

1)粘滞摩擦力。由于动子的速度v与粘滞摩擦力成正比，粘滞摩擦力是速度的非线性函数，因此可以用速度轴前馈补偿来消减粘滞摩擦力对伺服系统的恶性影响。

2)滑动摩擦力。由于直线电动机在运行中将受到上千牛顿的法向吸引力，动子所受到的法向吸力与滑动摩擦力成正比，这就导致滑动摩擦力较大，因直线电动机不可避免地受到来自滑动摩擦力的扰动。

1.2 系统内部成因

1.2.1 齿槽效应

由于定子磁场与动子铁心相互作用，使得所有的开槽永磁直线电动机中都存在着齿槽力。当永磁直线电动机沿轨道运动时，由于经过定子齿磁通路径的不同，使得定子齿受到的永磁体吸引力的方向和大小均不相同，致使其合力不为零而产生齿槽推力波动。

1.2.2 纹波推力

在PMLSM中，通过将动子电枢的相电流及其反电动势设计为正弦来使其产生定值推力。由于驱动电流的非正弦和反电动势的非正弦的原因，导致电流谐波存在，从而产生了推力波动。由于逆变器输出的三相电流是由直流电逆变得到的，因此电流中必然会含有一定的导致推力脉动的谐波。通过对驱动电流波形进行改善，合理优化直线电动机极弧系数能够有效降低纹波推力对伺服系统工作产生的扰动［2］。由于直线电动机永磁体充磁不均匀，再加上自身温度及周围环境对永磁体工作的影响，导致永磁体磁链中产生一定的谐波，这样的谐波可以通过优化永磁体的性能来消减其对于直线电动机伺服性能的影响。

1.2.3 电机参数改变

在PMLSM运行过程中，由于磁路饱和温度变化会实时导致直线电动机自身绕组自感、互感、电阻的变化。因此依照直线电动机额定参数设计的原始调节控制系统会由于这些变化而无法实现原有的控制，以导致直线电动机性能下降。

1.2.4 磁阻推力波动

磁阻推力波动是由定子磁阻变化和动子绕组电流激励磁场互相作用的结果。对于表面凸装式磁极的直线电动机，其磁阻推力波动对直线电动机工作平稳性的影响不明显，而凸极直线电动机中的定子磁阻却变化较大，动子绕组电感会跟随转子角度的改变而发生改变［3］。

1.2.5 电流时滞谐波

控制量传输与被控量的反馈滞后分别由逆变器传输滞后与转速测量滞后导致，这种现象在高性能伺服系统中比较常见。由于这些滞后的存在，致使直线电动机调控机制不能及时生效，扰动干扰也无法及时发现与补偿，使得整个控制系统出现振动、超调、输出不稳定等不良现象。

1.2.6 端部效应

静态纵向边端效应是由于直线电动机铁心两端的断裂所导致的各相绕组互感不等以及运行过程中反向行波磁场和脉振磁场存在而产生的。动态纵向边端效应则是由于直线电动机的次级相对于初级以较高速度运动时，在次级的进出两端而产生的磁场畸变［4］。除此之外，一般情况下，直线电动机次级宽于初级，由于这种实际的结构影响，致使PMSLM的运行不可避免地受到静态横向端部效应的干扰。当直线电动机初级次级发生相对运动时，横向磁场密度分布的不均匀现象称为动态横向端部效应［1］。

2 推力波动抑制策略

PMLSM在以高精密、高切削为主的先进制造业中使用日益广泛，然而推力波动的存在，使其运行时产生噪声、抖动甚至引起共振，运动不平稳直接导致其伺服精度下降。因此长久以来推力波动成为了研究PMLSM的主要问题，解决方法主要有两方面:一是从直线电动机结构设计角度入手;另一方面是针对运行过程中产生的相关问题，从系统控制手段上着手。

2.1 电机设计角度抑制推力波动

2.1.1 优化齿槽结构

推力波动可以从将齿槽结构设计成分数槽来抑制。文献［7］研究了24槽22极齿槽力形成原理及周期分布规律，并且应用有限元方法分析整数槽、分数槽及其不同齿槽结构及尺寸等状态下相应的齿槽力。首先将周期边界条件加在次级两端，然后把PMLSM次级等效成无限长，用这种方法可以有效地消除端部效应的影响。结论证明，齿槽力可以通过分数槽得到很好的控制［7］。

2.1.2 优化动子铁心结构

在对直线电动机的端部效应力进行分析时，采用了将有限元分析和数理分析相结合的分析方式，提出了针对削弱直线电动机端部效应力的抑制方法，分析结果表明端部效应力可以通过优化端部结构和动子沿运动方向的长度得到有效控制。在不考虑齿槽效应的情况下，为使端部效应最小，动子长度应满足:

式中:k为整数;τ为极距。但单一优化动子长度并不能完全消除端部效应力，从根本上讲，端部效应是端部磁阻突变造成的，因此可以采取优化直线电动机端部结构，目前最有效的方式是在动子铁心两端采用倒角结构［5］。

2.1.3 斜槽技术

试验研究证明，通过将动子槽的位置相对于永磁体转动一个极距，可以有效减小直线电动机定子的磁阻变化，从而减小齿槽效应，减弱推力波动对直线电动机的影响。

2.1.4 优化磁极结构

经研究实验证实，将磁极设计成弧形磁极，能有效减小PMLSM推力波动［6］。

2.2 控制角度抑制推力波动

2.2.1 精密工作台前馈补偿方法

文献［7－8］都是利用推力波动与直线电动机速度位置建模，然后设计相应的前馈补偿方法来抑制体力波动。在一些机械结构已经固定的精密工作台专用直线电动机中，推力波动的产生主要来自于运动速度，文献［7］采用PD+AF+DOB(比例微分+速度前馈+推力波动前馈)方法来减小推力波动引起的跟踪误差。该结构主要包括三个模块推力波动频率估计器f(α)、带动滤波器w(α)、推力波动调节器f(z)。该方法跟扰动观测器相比，不但具有结构简单、计算量小的优点，而且可以提高精密工作台的跟踪精度［7］。

文献［8］利用SVM(支持向量机)进行推力波动模型参数识别，同时推力波动是采用自适应补偿控制策略进行抑制。系统控制方案如图1所示，该系统由两个前馈单元和一个反馈单元组成，其中基本PID反馈单元用于保证整个系统的稳定性;推力波动补偿环节用于补偿推力波动引起的误差;逆线性模型前馈单元则用于加速跟踪响应速度。该方案使直线电动机的轨迹跟踪精度得到整体提高，并用MATLAB进行仿真，结果表明，该控制系统具有更小的轨迹跟踪误差、更强的抗干扰性，使得直线电动机定位精度进一步提高。

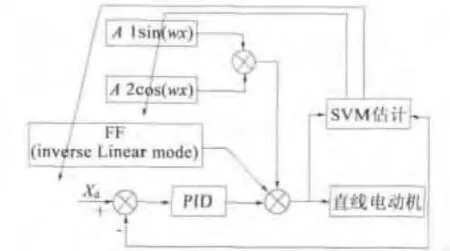
图1 PID加推力补偿控制方案

2.2.2 标准迭代学习控制减小推力波动

文献［9］以迭代学习(Iterative Learning Control)为基础，提出了相应的PMSLM控制方法，迭代学习过程如图2所示，统计系统最近一次的轨迹跟踪误差，再根据迭代学习律，通过计算生成一组新的迭代学习输出信号，进而优化当前的误差输出，并传输到控制器中，以提高系统轨迹跟踪的特性。与此同时，为了使迭代学习控制器能更好地反映工作系统的动态性能，运用脉冲响应矩阵来设计迭代学习器，并依据当前跟踪误差计算所需的控制量，进一步完善前一次的控制指令，迭代学习算法可以极大地抑制推力波动对系统的影响，提高系统的轨迹跟踪性能［9］。

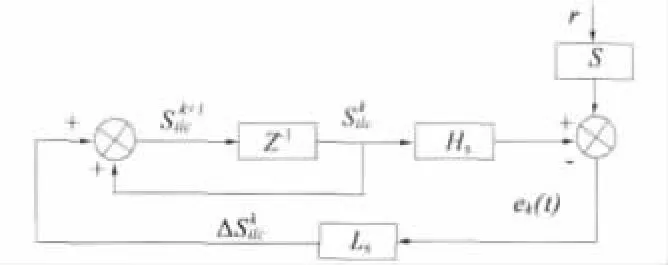
图2 迭代学习过程

2.2.3 现代控制策略减小推力波动

1)滑模变结构控制

变结构控制实质上是一种不连续性的特殊非线性控制。由于滑动模态与控制对象以及参数扰动无关，并且可以在动态过程中，根据系统当前状态目的性地变化，从而使系统按照预定“滑动模态”的状态轨迹运动。这就使得变结构控制具有对扰动及参数变化不敏感，并且响应速度快、可离线设计与辨识等优点［10］。因此，滑模变结构控制广泛应用于伺服系统中，但其推力波动多引起的颤抖问题却限制了其广泛应用的主要原因。孙宜标等人利用滑模变结构控制使工作系统对外部扰动及电机性能参数在运行中的变化具有自我调节的特点，研究出带有推力观察器的直线式交流伺服系统滑模变结构控制，在很大程度上解决了传统滑模控制所带来推力波动问题［11］。

2)鲁棒控制

采取频域方法和代数方法来控制对象模型的不确定性，并设法保持系统的稳定性和品质的鲁棒性。频域方法是从系统的传递函数矩阵角度上来设计系统，其中H∞控制是应用最为普遍的控制方法，直线伺服系统的速度控制器就据此来设计，这种控制策略旨在使系统的由扰动至偏差的传递函数矩阵的H∞范数取得极小值，实验证明该方法可以有效地抑制推力波动［12］。文献［13］系统通过采用自适应鲁棒控制的控制方式，实现了高精度、高速度的运动目的。

3)自适应控制

一般情况下，自适应控制策略主要降低或消除直线伺服电动机的特征参数变化缓慢类型的扰动以及其他外部因素对系统运动性能产生的干扰［14］。文献［15］阐述了利用自适应学习方法改善PMLSM的轨迹跟踪性能，并将该控制算法分为两部分，其中一部分用于增强系统的鲁棒性，保持系统在单次运动模式下的稳定状态;另一部分通过执行重复任务，自适应学习项补偿系统的非线性［15］。这种控制方式可以有效提高直线电动机的运动稳定性及轨迹跟踪精度。

4)预测控制

预测控制是一种针对干扰信号的未来及目标值任何情况都已知条件下，力使目标值与被控量间偏差最小的控制方法［14］。郭庆鼎等人已经成功利用预测控制理论减小了直线电动机控制系统中的推力波动对其运动的影响。

5)智能控制策略

人工神经网络控制、模糊控制和专家控制是智能控制中比较典型三种控制策略。人工神经网络控制是模拟人的大脑中枢神经进行系统设计，自我学习能力较强，并具有联想存储和快速寻找最优解的能力。主要通过实时修正网络权值手段来调整系统输出以获得与期望最贴近的输出结果。文献［16］则提出了一种利用扰动观测器进行纹波推力补偿方案，为了增强补偿效果，采用基于BP算法的前馈神经网络去进一步逼近和抑制纹波推力，但是该方法计算量较大，在实际系统中无法保证其实时性。模糊控制系统的鲁棒性好，极大地削弱了干扰和参数变化对控制效果的影响，尤其适用于非线性、时变及纯滞后系统的控制，已出现在伺服工作系统中［17］。通常情况下专家控制在伺服系统中的研究及应用较少，其主要应用于复杂控制系统。

为进一步削弱直线电动机的“抖振”问题，也有研究人员将人工神经网络控制与现代控制理论中的滑模变结构控制相结合，孙宜标、郭庆鼎等人利用滑模变结构控制理论，设计了具有强鲁棒性的速度控制器，同时采用基于人工神经网络前馈给定补偿的滑模控制测量来加强直线电动机运行的平稳性。经仿真研究证明，该方案针对端部效应所产生的推力波动干扰具有很好的抑制作用，对系统参数变化及推力扰动具有很强的鲁棒性，而且整个系统的稳态性能得到了充分的提高［18］。

3 结 语

随着工业的发展，人们对精密仪器的要求日益增高，这就意味着直线电动机的发展前景日益广阔，但其推力波动问题成为了限制其广泛应用的主要问题，本文基于对PMLSM的相关研究，详尽地分析了推力波动产生的原因，并综合阐述了相关的抑制策略，这些方法在一定程度上产生了明显的抑制效果，但依然存在局限性，针对PMLSM推力波动问题的研究将继续下去。

［1］郭庆鼎，王成元.直线交流伺服系统的精密控制［M］.北京:机械工业出版社，2000.

［2］李庆雷，王先逵，吴丹，等.永磁同步直线电机推力及垂直力的有限元计算［J］.清华大学学报(自然科学版)，2000(5):20－23.

［3］纳斯尔 S A，波尔达 I.直线电动机［M］.北京:科学出版社，1982.

［4］叶云岳.直线电机原理与应用［M］.北京:机械工业出版社，2000.

［5］杨康.永磁直线同步电机推力波动分析与抑制［D］.沈阳:沈阳工业大学，2013.

［6］TAVANA N R，SHOULAIE A.Pole－shape optimization of permanent－magnet linear synchronous motor for reduction of thrust ripple［J］.Energy Conversion and Management，2011，(52):349 －354.

［7］杨开明，叶佩青，尹文生.精密工作台直线电机推力波动补偿研究［J］.控制与检测，2005(8):32－36.

［8］李竣，黄宴委，鲁云飞，等.基于支持向量机的直线电机推力波动前馈补偿［J］.微电机，2012，45(7):61 －64.

［9］张明超.永磁同步直线电机推力波动建模与抑制方法研究［D］.北京:清华大学，2010.

［10］高为炳.变结构控制理论基础［M］.北京:中国科学技术出版社，1990.

［11］孙宜标，郭庆鼎，王丽梅.基于推力观测器的直线式交流伺服系统滑模变结构控制［J］.电工技术学报，1998，13(2):1 －5.

［12］孙艳娜，刘爱民，郭庆鼎.直线永磁同步伺服电机的鲁棒速度控制器的设计［C］//2000中国控制与决策学术年会论文集.沈阳:东北大学出版社，2000:82－86.

［13］LU L，YAO B，WANG Q F，et al.Adaptive robust control of linear motors with dynamic friction compensation using modified luGre model［J］.Automatica，2009，45:1840 －1848.

［14］邹积浩.永磁直线同步电机控制策略的研究［D］.杭州:浙江大学，2005.

［15］宋一旭，王春洪，尹文生，等.永磁直线同步电动机的自适应学习控制［J］.中国电机工程学报，2005，25(20):151 －156.

［16］ZHANG D L，CHEN Y P，AI W，et al.Precision motion control of permanent magnet linear motor［J］.International Journal of Advanced Manufacturing Technology，2007，35(3):301 －308.

［17］GUO Q D，WANG L M，LUO R F.Robust fuzzy varibale structure control of PMLSM servo system［C］//IEEE International Conference on Intelligent Proceedings Systems.1997:675 － 679.

［18］孙宜标，郭庆鼎.基于神经网络给定补偿的交流永磁直线伺服系统滑模控制［J］.电工技术学报，2002，17(3):21－25.