面向应急任务卫星鲁棒性规划模型及算法

邓润，唐宏，单越，牛晓楠，刘颖慧

（北京师范大学 地表过程与资源生态国家重点实验室，北京 100875）

1 引 言

成像卫星具有一次成像范围大、成像成本低等特点，已广泛应用于国防、环保、农业、气象、灾害应急等领域。然而，成像卫星研制、发射和维护成本高，尽管随着卫星应用技术的发展，越来越多的成像卫星升入太空，但相对于人类日益增长的成像需求，卫星资源仍然异常宝贵。为了最优化地利用成像卫星资源，卫星任务规划尤为重要。成像卫星受到轨道限制仅在特定的时间窗口内与地面目标可见，卫星任务规划［1］即综合考虑卫星成像能力及任务需求等约束，以安排最大任务收益为优化目标，确定要执行的任务及执行这些任务的时间窗起止时间。现有研究［2－6］大多集中在卫星静态任务规划，当新的应急成像任务到来时，采用完全重规划算法对原问题重新建模求解。产生的新任务规划方案与初始方案相差较大，导致卫星重调度难度大。

针对卫星动态任务规划，Perberton等［7］总结了4种引起卫星任务规划方案调整的因素：任务观测机会变化、资源变化、新任务插入、卫星任务规划问题参数变化，但并未提出具体的问题模型及求解算法。Verfaillie［8］和刘洋［9］提出基于动态约束满足问题的卫星动态任务规划模型及求解算法，但并未考虑初始方案的可调整性。王军民［10］将卫星任务动态规划问题分为鲁棒性初始方案生成及调整两个阶段，在初始方案生成阶段，引入基于邻域的鲁棒性指标，得到更易于调整的初始方案，当新任务与初始方案中的任务冲突时，能使初始方案中的任务安排到其他位置而不被删除，但基于邻域的鲁棒性指标不能衡量初始方案接受新任务直接插入而不影响已安排任务执行的能力。

本文在卫星鲁棒性任务规划模型目标函数中引入总时间重叠度及总任务执行时长两项鲁棒性指标，通过仿真模拟实验结果分析可知，在任务收益和相差不大的情况下，采用本文方法能得到总时间重叠度更小，总任务执行时长更短的卫星鲁棒性任务规划方案。

2 卫星鲁棒性任务规划模型

2.1 鲁棒性指标

对于给定的规划方案，在面临扰动时，应用某种特定的动态调整方法既能保持良好的规划方案收益，又能保持新老规划方案的差异尽可能小，则称之为鲁棒性规划方案［10］。

本文提出两项鲁棒性指标：①总任务执行时长，衡量规划方案接受新任务直接插入而不影响已安排任务执行的能力；②总时间重叠度，衡量规划方案中已安排任务与新任务冲突时，能被重新安排在其他时间窗口执行的能力。

定义1总任务执行时长：各卫星安排执行任务时间之和。

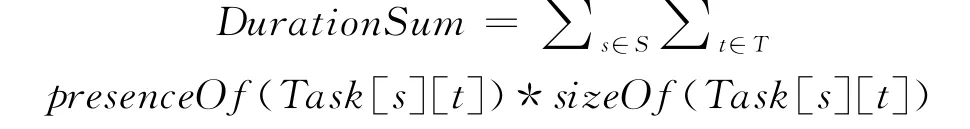
（上式中涉及的变量、函数意义见2.2节模型中涉及的变量、参数及函数部分）

总任务执行时长算例：

表1 各任务收益及卫星a与任务可见时间窗口

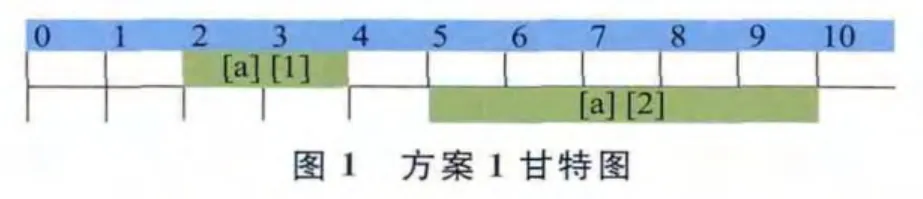
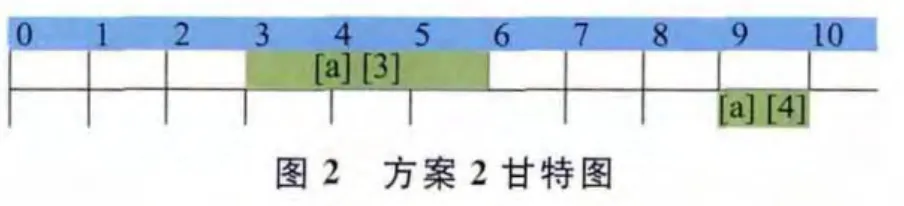
表1列举出卫星a与4个待执行任务间的可见时间窗口、任务收益及卫星完成各拍摄任务需要的时长。其中，任务收益根据各任务的重要性设定，任务越重要，卫星执行任务获得的收益越高，卫星任务规划方案的任务收益和即方案中所有已安排执行任务的收益和。由图1可知，方案1中卫星a最终执行任务1和任务2；图2显示方案2中卫星a执行任务3和任务4，两方案任务的收益和均为4，方案1总任务执行时长＝2＋5＝7，方案2总任务执行时长＝3＋1＝4。在规划时段0～10内，显然方案2的空余时间窗口更多，接受新任务直接插入能力更强。此外方案2总执行时长短，卫星能量消耗更低，因此任务收益和指标相同的情况下，总任务执行时长越短的方案性能越好。

定义2 总时间重叠度：各卫星执行任务时间窗口与卫星其余可见时间窗口的时间重叠度乘以任务权重的和。

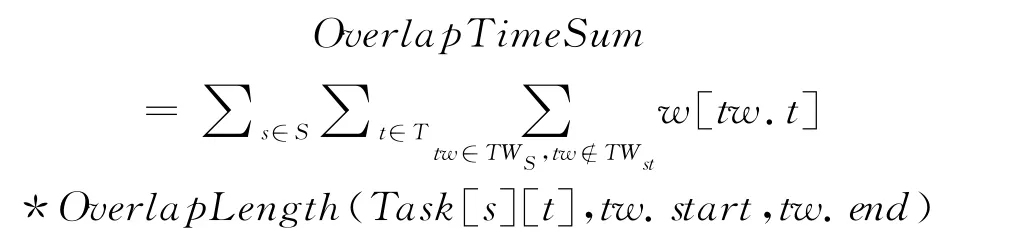
（上式中涉及的变量、函数意义见2.2节模型中涉及的变量、参数及函数部分）

总时间重叠度算例：

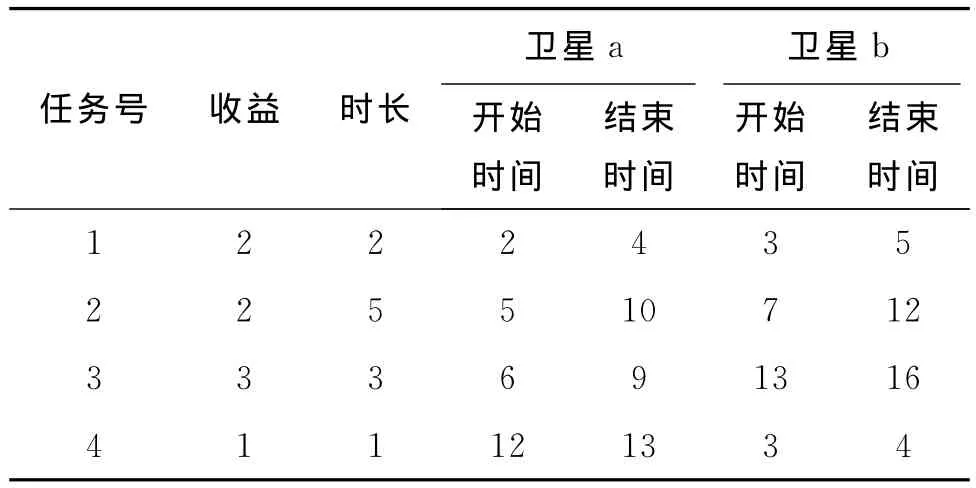
表2 各任务收益及其与卫星a，b可见时间窗口

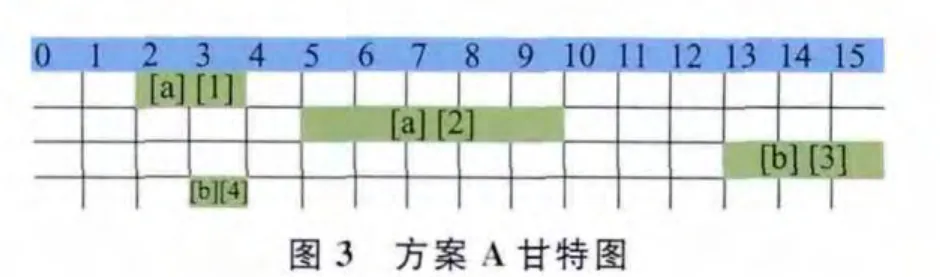
由图3、图4可知，方案A、方案B的任务收益和指标均为11，方案A总时间重叠度＝3×3＋2×1＝11，方案B总时间重叠度为0，当新应急任务到来要占用任务1或者任务3的时间窗口时，方案A总时间重叠度较高，能重新安排任务1的潜在时间窗口［3 5］与任务4重叠，能重新安排任务3的潜在时间窗口［3 6］与任务2重叠，导致任务1、任务3都无法重新安排。而方案B总时间重叠度为0，能重新安排任务的潜在时间窗口都与方案中的其他任务没有重叠，故当新应急任务插入引起冲突时，冲突位置的任务能重新安排到其他时间窗口执行，无需删除，因此任务收益和指标相同的情况下，总时间重叠度小的任务规划方案更优。

2.2 面向应急任务卫星鲁棒性任务规划模型

本文引入总任务执行时长、总时间重叠度两项鲁棒性指标，建立的卫星鲁棒性任务规划约束满足问题模型如下：

以上各式表达的含义如下：

式（1）表示任务收益和最大；

式（2）表示总时间重叠度最小；

式（3）表示总任务执行时长最短；

式（4）表示每个任务最多被执行一次；

式（5）表示每颗卫星的执行任务序列中不存在重叠的时间段，即各卫星同一时间仅执行一个任务；

式（6）表示卫星执行任务必须在两者可见时间窗口内进行；

式（7）表示任意单圈时间段内，卫星执行任务的总时长必须小于卫星单圈最长执行任务时长。

模型中涉及的变量、参数及函数：

（1）决策变量：

Task［s］［t］：时间区间变量（interval），表示卫星s执行任务t的时间窗口；

Satellites：将卫星s执行任务的时间窗按时间顺序排序得到的任务序列，表示卫星s的执行任务序列。

（2）其他参数：

ω（t）：成像任务t的收益；

tw：卫星与任务间可见时间窗口四元组＜s，t，start，end＞，对应信息＜卫星，任务，开始时间，结束时间＞；

TW：可见时间窗口集合；

TWs：卫星s的可见时间窗口集合；

TWst：卫星s对任务t的可见时间窗口集合；

S：参与成像卫星集合；

T：成像任务集合；

maxdurations：卫星s单圈最长执行任务时长；

orbittimes：卫星s单轨运行时间。

（3）函数：

presenceOf（interval a）：若a在调度方案中出现则返回1，否则返回0；

sizeOf（interval a）：返回a的大小；

overlapLength（interval a，int b，int c）：返回a与［b c］间重叠时间长度；

startOf（interval a）：返回时间区间变量的开始时间。

3 卫星鲁棒性任务规划算法

3.1 基于NSGA－П卫星鲁棒性任务规划算法

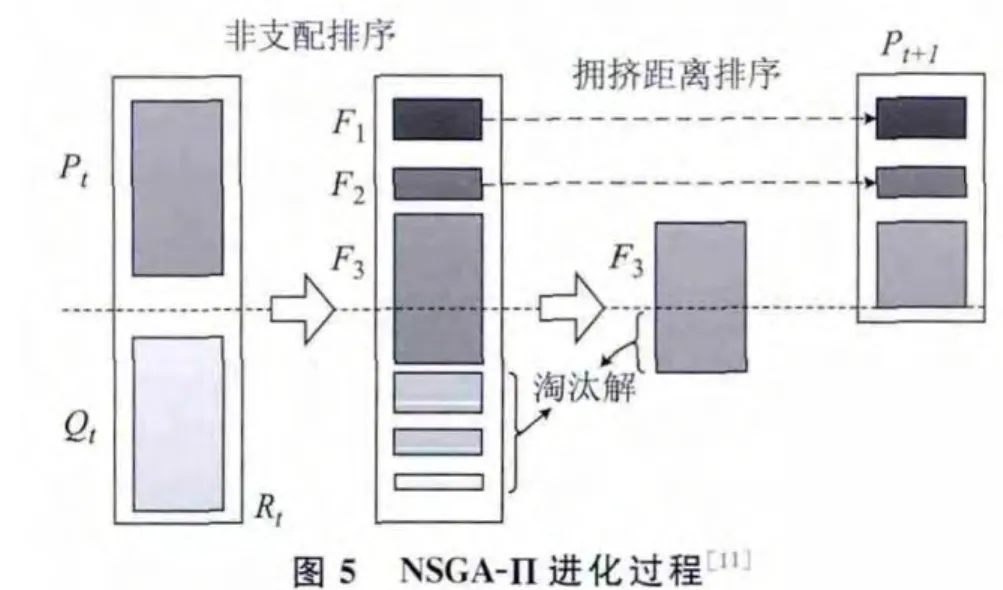
卫星鲁棒性任务规划问题是典型的多目标优化问题，目前求解多目标优化问题大多采用多目标进化算法。针对上述卫星鲁棒性任务规划模型，本文基于经典多目标优化算法 NSGA－П［11－12］框架（图5）设计了卫星鲁棒性任务规划算法。

算法流程如下：

（1）设计解的遗传编码，设置种群大小M，最大迭代次数T，当前迭代次数t＝0，并初始化种群Pt；

（2）对种群Pt进行选择，交叉，变异遗传操作，产生新种群Qt；

（3）对新种群Rt＝（Pt∪Qt）进行非支配排序（Non－dominated sorting）得到Rt的非支配前沿F＝（F1，F2，…）；

（4）令Pt＋1＝Ø，i＝1，Pt＋1＝Pt＋1∪Fi；

（5）i＝i＋1，若｜Pt＋1｜＋｜Fi｜＜M，转（4），若｜Pt＋1｜＋｜Fi｜＝M，转（7）；

（6）计算Fi中个体的拥挤距离，并按拥挤距离选出最好的｜M－｜Pt＋1｜｜个体，Pt＋1＝Pt＋1∪Fi［1∶｜M－｜Pt＋1｜｜］；

（7）t＝t＋1，若t＋1＜T且Pt＋1∩Pt≠Pt，重复（2）；

（8）输出Pt中的非支配pareto解并解码。

3.2 遗传算子设计

3.2.1 遗传编码

由于卫星任务规划问题中，个体遗传操作（交叉、变异）涉及到大量的基因位置移动，本文采用实数链状编码，将卫星按编号顺序排列，每颗卫星任务序列包含一对虚拟起始、终止节点，两者之间所夹节点为该卫星执行的任务节点，相邻卫星间通过虚拟的起始节点与终止节点连接。为便于遗传个体的解码及任务插入的可行性分析，本文设计的任务节点包含以下信息：任务号、占用的可用时间窗口开始时间、占用的时间窗口终止时间、最早开始执行时间、最晚开始执行时间、关键任务序列编号、后向能量负荷、指向下一任务节点的指针、指向前一任务节点的指针。具体遗传编码示例如图6所示。

3.2.2 选择算子

采用二元锦标赛选择，从种群中随机选取2个个体，比较这2个个体在非支配排序中的顺序，选取位置靠前的个体。

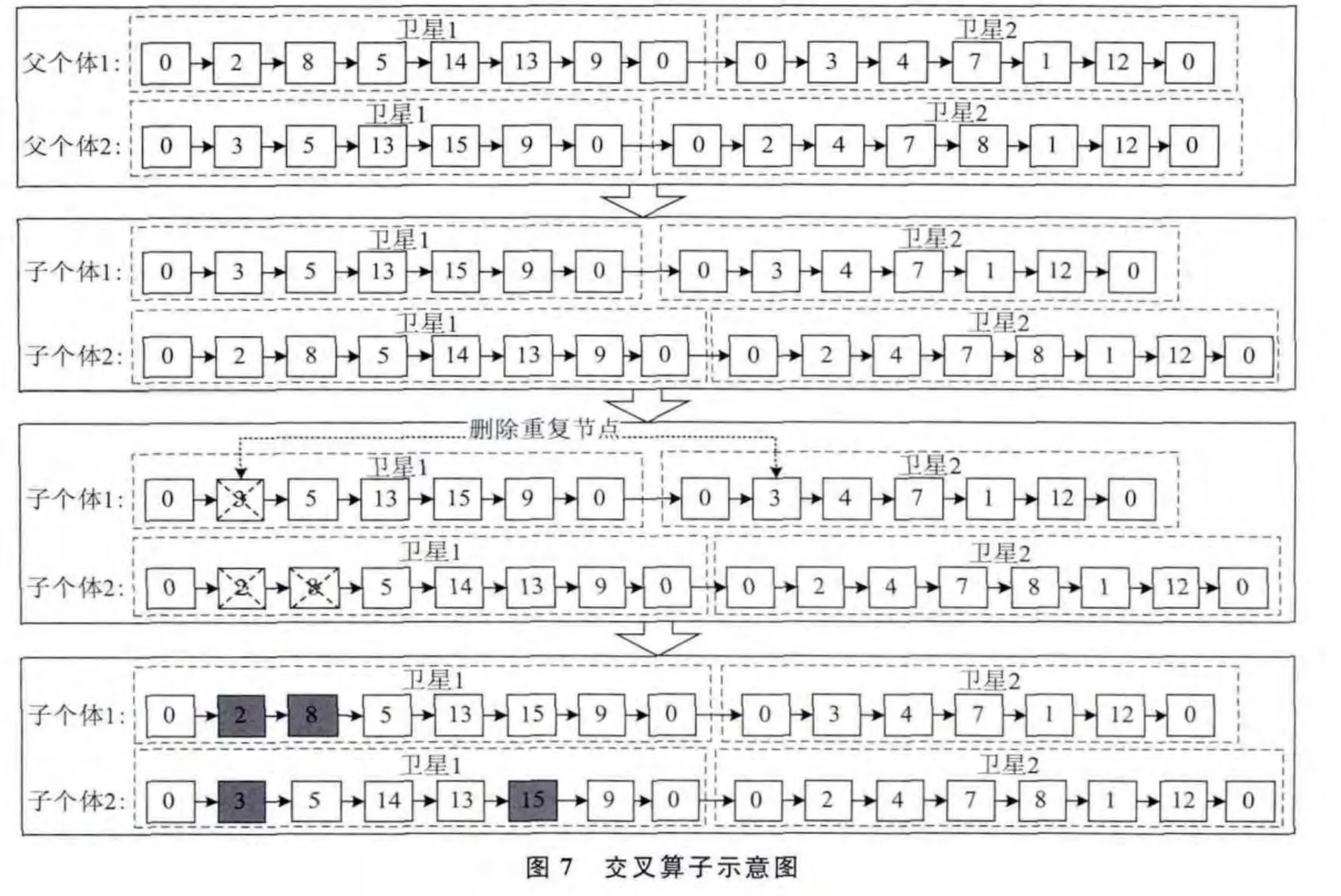
3.2.3 交叉算子

根据上述遗传编码，设计交叉算子（图7）：在两个父个体上，随机选择同一颗卫星的任务序列互相替换；在父个体其他卫星的任务序列上删除与新替换的卫星任务序列重复的任务；并尝试插入新替换的卫星任务序列相比原始任务序列丢失的任务。

3.2.4 变异算子

根据成像任务多时间窗口特性，设计单点变异算子，具体工作流程如下：

①对原始任务序列（1，2，3，4…nt）进行随机排序，初始化任务序列号i＝1；

②计算任务Ti对应的时间窗口数量nitw；

③若nitw＝0，i＝i＋1，转到（2）；

④若待变异染色体中不存在Ti，尝试插入任务Ti。若插入成功，更新染色体，结束变异；若插入失败，i＝i＋1，转到（2）；

⑤判断Ti在染色体中的位置能否改变，若能，改变Ti位置，更新染色体，结束变异；否则，删除Ti，更新染色体，结束变异。

3.3 种群初始化

①初始化任务序列号i＝1，个体编号j＝1，种群大小M；

②初始化调度方案任务链Schedulej＝φ，对原始任务序列（1，2，3，4…nt）进行随机排序；

③选取任务Ti插入，设任务Ti对应的时间窗口数量nitw；

④若nitw＝0，转到（7）；否则将任务Ti对应的时间窗口进行随机排序，k＝1；

⑤选取时间窗口TWk，若任务Ti在时间窗口TWk能够插入到调度方案中而不引起冲突，更新Schedulej，转到（7）；

⑥k＝k＋1，若k≤nitw，转（5）；

⑦i＝i＋1，若i＞nt，转（8）；否则，转到（3）；

⑧j＝j＋1，若j≤M，i＝1，转到（2）；否则，种群初始化结束。

4 实验及分析

4.1 实验方案设计

假设有2颗卫星，分别选取50，100，200个点目标成像，通过STK软件计算卫星与观测目标间的可见时间窗口，并随机模拟各观测目标要求的成像时长及任务收益。

常规卫星任务规划往往仅以任务收益和最大为优化目标，不考虑鲁棒性指标。鲁棒性任务规划研究中王军民［12］提出基于邻域的鲁棒性指标。针对上述不同观测目标数量的3组输入数据，将本文提出的基于总时间重叠度及总任务执行时长指标的鲁棒性任务规划方案，分别与常规卫星任务规划方案和基于邻域指标的鲁棒性任务规划方案对比分析。

4.2 基于总时间重叠度和总任务执行时长指标的鲁棒性卫星任务规划方案与常规方案对比

针对上述不同观测目标数量的3组输入数据，仅以任务收益和最大为优化目标建立卫星任务规划模型，采用遗传算法求解；同时以任务收益和最大、总时间重叠度最小、总任务执行时长最短为优化目标建立卫星鲁棒性任务规划模型，采用本文提出的基于NSGA－П的卫星鲁棒性任务规划算法求解。比较每组数据在两种情况下得到的最优规划方案任务收益和、总时间重叠度、总任务执行时长3项指标（图8～图10，表3～表5），考虑三优化目标得到的Pareto最优解数量较多，仅列出收益指标与单优化目标得到的任务收益和相差10以内的规划方案指标函数值。

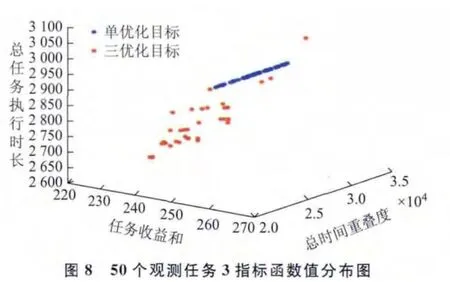
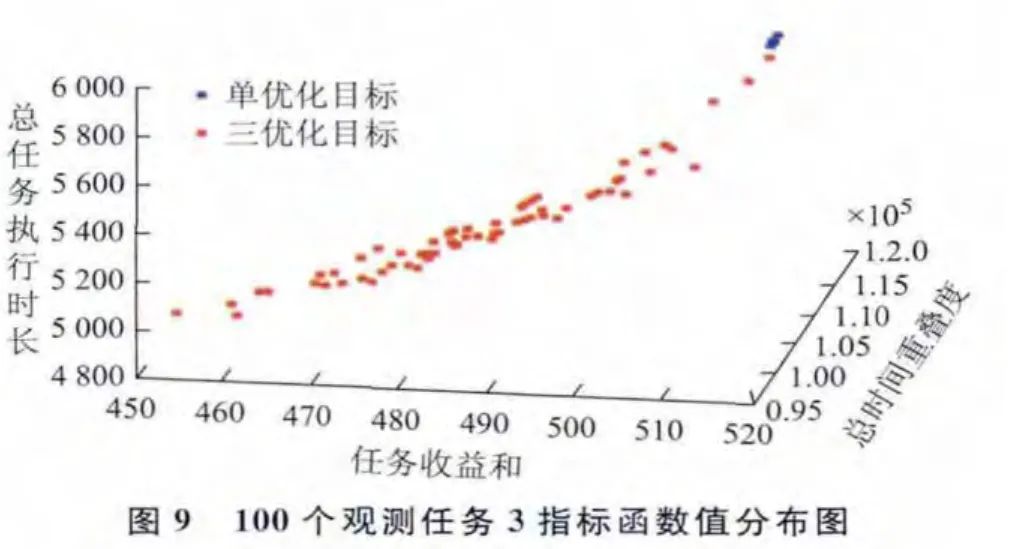
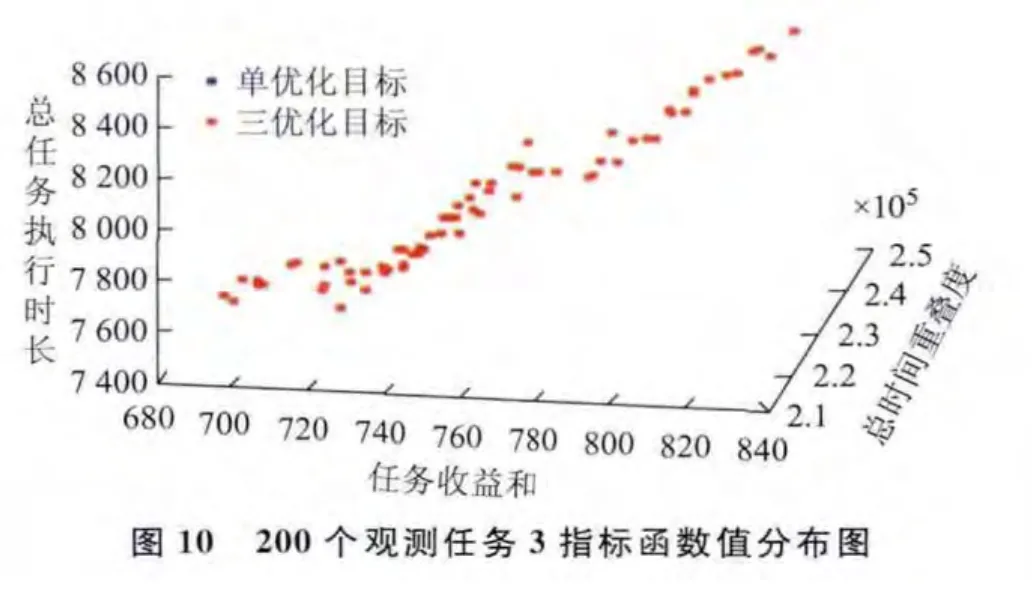
表3 50个观测任务3指标高收益区具体数值列表

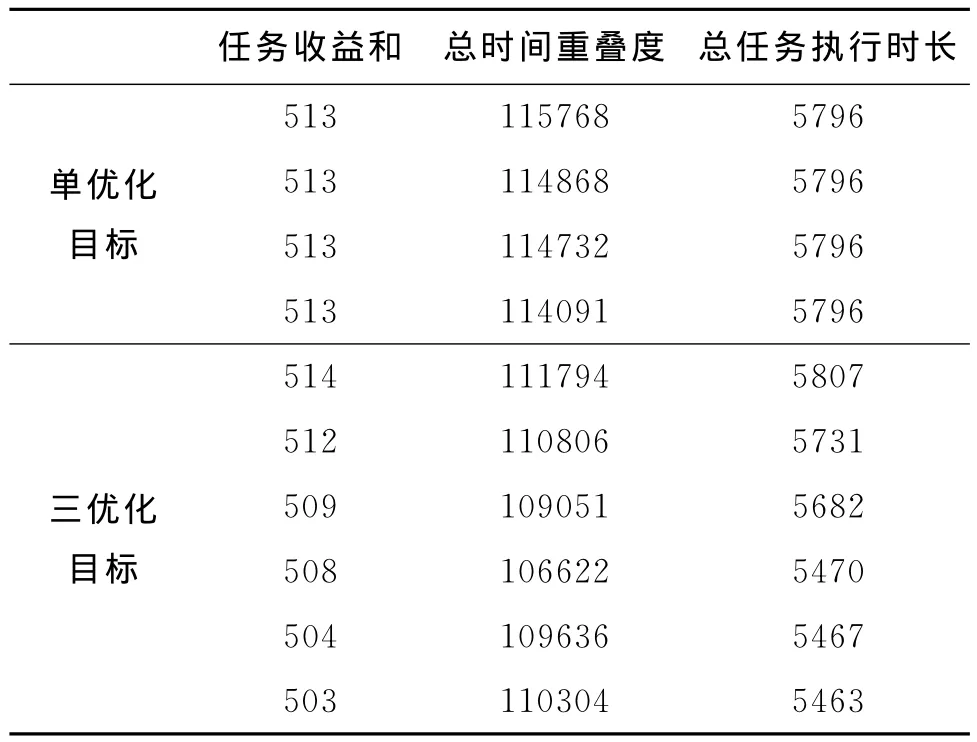
表4 100个观测任务3指标高收益区具体数值列表

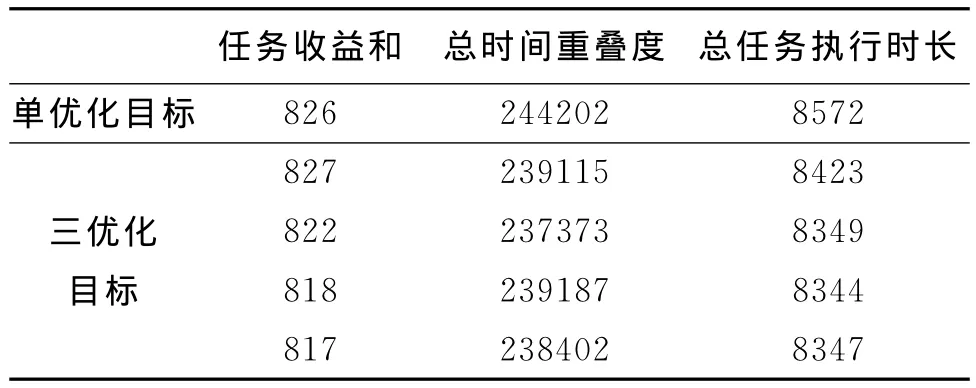
表5 200个观测任务3指标高收益区具体数值列表

分析图8～图10，及表3～表5可知，相比单优化目标思想的常规卫星任务规划，本文提出的三优化目标方法能得到任务收益和相差不大，但总时间重叠度及总任务执行时长都有大幅度减小的规划方案。此外，三优化目标方法不容易陷入局部最优，能进化得到任务收益和更大的规划方案，以及多个高收益、总时间重叠度和总任务执行时长较小的规划方案供决策者选择。

4.3 基于总时间重叠度、总任务执行时长指标与基于邻域指标的鲁棒性任务规划方案对比

针对上述3组实验数据，分别求解基于邻域指标与基于总时间重叠度、总任务执行时长指标的两种卫星鲁棒性任务规划模型，并比较两种规划方案的任务收益和、总任务执行时长、方案中可调整的任务收益和指标（图11～图16）。

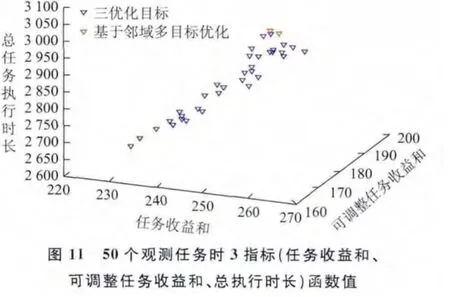
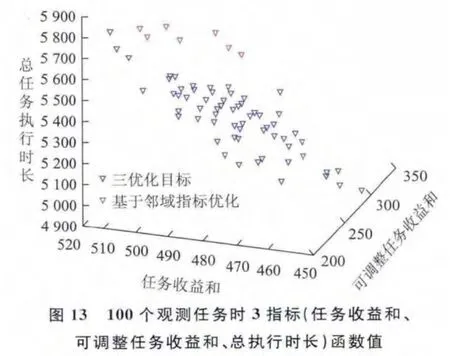
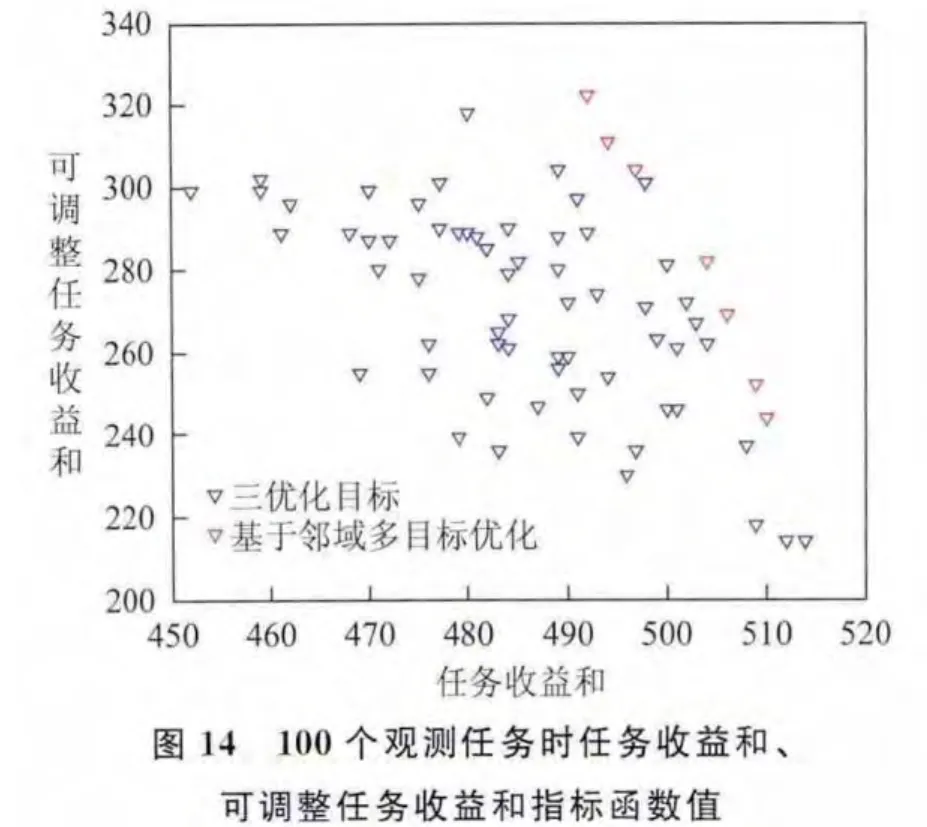
分析图11～图16可知，在任务收益和指标值较大时，基于总时间重叠度、总任务执行时长指标与基于邻域指标的鲁棒性任务规划方案相比，两种规划方案的任务收益和、可调整任务收益和指标都相差不大，基于总时间重叠度、总任务执行时长指标得到的规划方案总任务执行时长更小。

5 结束语

本文提出总任务执行时长、总时间重叠度两项新鲁棒性指标，建立成像卫星鲁棒性任务规划模型，并设计基于NSGA－П的卫星鲁棒性任务规划算法求解该模型。实验表明，在考虑任务收益和最大化的基础上，引入总时间重叠度及总任务执行时长的三优化目标模型、仅考虑任务收益和指标的单优化目标模型（常规卫星任务规划方案）、基于邻域鲁棒性指标的多目标优化模型，三者得到的任务总收益高且相差不大的规划方案相比，本文方法得到的卫星任务规划方案总时间重叠度、总任务执行时长往往更小，当新应急任务到来时，将有更长的空余时间段接受其直接插入而不引起冲突，且与其冲突的原始任务能调整到其他时间窗重新安排而不被删除的概率也更大。此外，总任务时长越短，卫星能量消耗越小，采用本文方法得到的卫星任务规划方案，在降低卫星能量损耗方面也具有重要实践意义。

［1］王沛，谭跃进.卫星对地观测任务规划问题简明综述［J］.计算机应用研究，2008，25（10）：2893－2897.

［2］VASQUEZ M，HAO J K.A “logic－constrained”knapsack formulation and a tabu algorithm for the daily photograph scheduling of an earth observation satellite［J］.Computational Optimization and Applications，2001，20（2）：137－157.

［3］BENSANA E，VERFAILLIE G，LEMAITRE M.Earth observing satellite［J］.Managements Constraints，1999，4（3）：293－299.

［4］FRANK J，SMITH D E.Planning and scheduling for fleets of earth observing satellites［C］.Proceedings of the Sixth International Symposium on Artificial Intelligence，Robotics，Automation and Space，2001.

［5］WOLFE W J，SORENSEN S E.Three scheduling algorithms applied to the earth observing systems domain［J］.Management Science，2000，46（4）：148－168.

［6］GABREL V，VANDERPOOTEN D.Enumeration and interactive selection of efficient paths in a multiple criteria graph for scheduling an earth observing satellite［J］.European Journal of Operational Research，2002，139（3）：533－542.

［7］PEMBERTON J C，GREENWALD L G.On the need for dynamic scheduling of imaging satellites［J］.International Archives of Photogrammetry Remote Sensing and Spatial Information Sciences，2002，34（1）：165－171.

［8］VERFAILLIE G，SCHIEX T.Solution reuse in dynamic constraint satisfaction problems［C］.AAAI，1994，94：307－312.

［9］刘洋，陈英武，谭跃进.一种有新任务到达的多卫星动态调度模型与方法［J］.系统工程理论与实践，2005，25（4）：35－41.

［10］王军民，王鹏，李菊芳，等.成像卫星鲁棒性调度策略研究［J］.系统工程与电子技术，2010，32（1）：109－114.

［11］DEB K，PRATAP A，AGARWAL S，et al.A fast and elitist multi－objective genetic algorithm：NSGA－II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182－197.

［12］DEBK，AGRAWAL S，PRATAP A，et al.A fast elitist non－dominated sorting genetic algorithm for multi－objective optimization：NSGA－II［J］.Lecture Notes in Computer Science，2000，19（17）：849－858.