双E型六维力传感器矩形梁强迫振动分析

谢黎峰，许德章

双E型六维力传感器矩形梁强迫振动分析

*谢黎峰1,2，许德章1,2

（1.安徽工程大学机械与汽车工程学院，安徽，芜湖 241000；2.安徽工程大学先进数控和伺服驱动技术实验室，安徽，芜湖 241000）

六维力传感器弹性体一般采用组合梁结构，每个分方向的输出信号中不可避免地存其它分方向的受力信号的耦合输出。在动载工作条件下，六维力传感器动态耦合输出非常复杂。为了从理论上揭示六维力传感器动态耦合输出的主要特征，本文以双E型六维力传感器中的矩形梁为对象，建立力学模型，采用弹性力学基本理论和达朗贝尔原理，选取矩形梁前三阶振型，推导出其它五个分方向受力在Mz主方向的动态耦合输出，并绘制出动态应变图，为六维力传感器动态解耦提供了理论依据。

六维力传感器；耦合；矩形梁；弹性力学；应变

六维力传感器用于测量三维空间的全力信息，即空间直角坐标系中，沿X、Y、Z三根轴线方向上的线性力Fx、Fy、Fz及绕X、Y、Z轴转动的力矩Mx、My、Mz[1]。目前，六维力传感器通常采用将电阻应变片贴在组合梁弹性体表面的结构。由于组合梁的整体式结构，六维力传感器任意一个方向的输出信号几乎与每一个力分量和力矩分量相关，属于耦合型结构，必须要进行解耦才能得到所需要的力信号[2]。六维力传感器的解耦一般可以分成静态解耦与动态解耦，从现有文献可以看出六维力传感器的静态解耦研究已经非常深入，而动态解耦研究则较少。

针对电阻应变片式六维力传感器的动态解耦问题，可以将动态解耦的方法大致上分为：不基于力学模型的解耦方法和基于力学模型的解耦方法。在不基于力学模型的解耦方法研究方面：中科院合肥智能研究所在自主研制的力/力矩标定试验台上，通过剪断吊砝码的绳索给被测力/力矩传感器施加阶跃激励力的方式，对六维力传感器动态特性进行初步研究；合肥工业大学徐科军等，基于不变性解耦的原理，提出了迭代动态解耦方法，对六维力传感器动态特性进行更进一步研究；东南大学宋国民等，提出利用矩阵对角优势化的方法设计补偿环节，使系统传递函数矩阵成为对角优势阵，实现弱化系统耦合的目的；哈尔滨工业大学丁明理等在传递函数矩阵分析法的基础上，应用小生境遗传算法进行解耦设计，直接利用多维力传感器的标定数据求解并优化解耦网络，避免建立多维力传感器传递函数模型的环节[3-6]。从这些解耦方法不难看出，由于避开六维力传感器动态耦合的力学本质，缺少必要的理论依据，难以获得理想的动态解耦结果。在基于力学模型的解耦方法研究方面，国内外均极少涉及，合肥工业大学刘正士教授和合肥智能机械研究所葛运建研究员等，曾试图将六维力传感器弹性体简化成六个集中质量的二阶阻尼系统，利用脉冲激励法对其动态性能做简单分析[7]，精确性与六维力传感器弹性体真实的力学特性相差甚远。本文从六维力传感器的动态耦合本质入手，基于弹性力学基本理论和达朗贝尔原理，对复杂弹性结构进行简化，建立简单的力学模型，充分揭示弹性体动力学特性[8-9]。

本文以双E型六维力传感器为例[10]，选取测量Mz方向力矩的弹性体矩形梁为研究对象，根据不同受力情况，将弹性体简化成梁、杆等力学模型，结合边界条件，推导出其他五个分方向受力在Mz主方向的动态耦合输出，为动态解耦提供理论依据。

1 双E型六维力传感器的结构和受力

1.1 六维力传感器结构

双E型六维力传感器结构如图1所示，其中上下E型膜5、7及矩形梁2构成传感器的弹性体，用于感知六维力和力矩；底座8、中心支柱6、中间传力环4及上传力环3可看作刚体；1为电阻应变片，贴在弹性体的表面。矩形梁各项参数见表1。

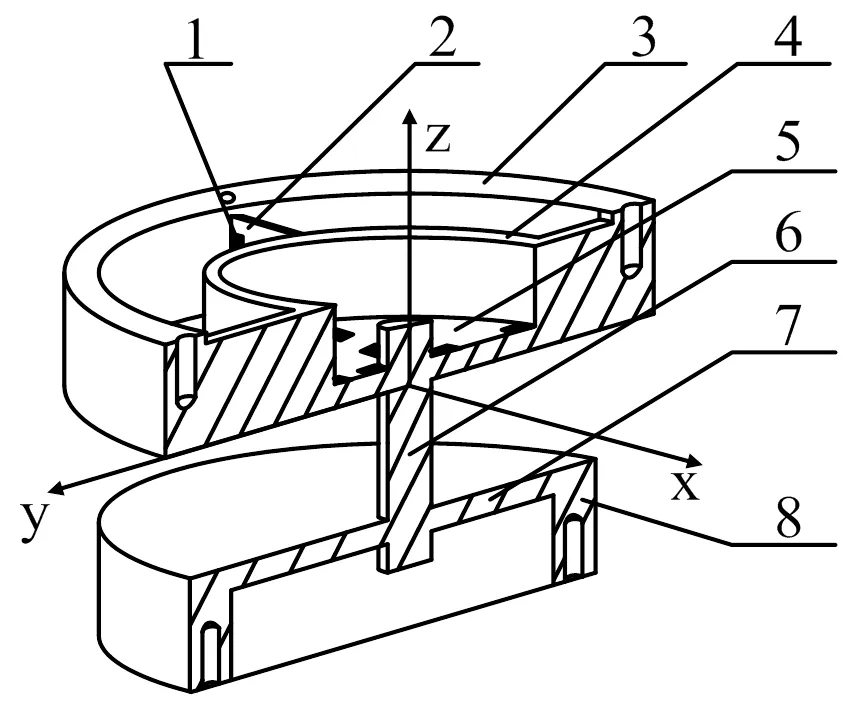
图1 六维力传感器的结构

1.2 六维力传感器弹性体力学模型的建立

给双E型六维力传感器施加载荷时，是将载荷作用在与上传力环通过螺钉连接的加载帽（图1中未画出）上。由于弹性体矩形梁与上传力环也连接在螺钉所在的位置，载荷被直接传递到矩形梁的边界上，产生如下四种受力情况：

（1）在六维力传感器受到动载荷Fz、Mx作用时，矩形梁1受力情况一致，如图2、图3所示，其一边都受到沿z轴方向的动载荷，另一边假定为固支边，整个矩形梁受力简化为梁的横向强迫振动；

（2）在六维力传感器受到动载荷My作用时，矩形梁1产生扭转变形，根据弹性力学，矩形截面杆的扭转理论求解该方向；

（3）在六维力传感器受到动载荷Fx、Mz作用时，矩形梁1受力情况一致，其一边都受到沿x轴方向的动载荷，另一边假定为固支边，整个矩形梁受力简化为薄板的横向强迫振动；

（4）在六维力传感器受到动载荷Fy作用时，如图4、图5所示，矩形梁1一边受到沿y轴方向的动载荷，另一边假定为固支边，将矩形梁受力简化为为杆的纵向强迫振动。

经计算，动载荷My作用时矩形梁1表面四个电阻应变片的桥路输出，即在Mz主方向的耦合输出为0；动载荷Fx作用时矩形梁1的变形与Mz主方向动载荷作用时情况一致，文献[9]已经求解出。因此，本文只讨论分方向动载荷Fz、Mx作用时梁的横向强迫振动和动载荷Fy作用时杆的纵向强迫振动问题。

表1 矩形梁相关参数

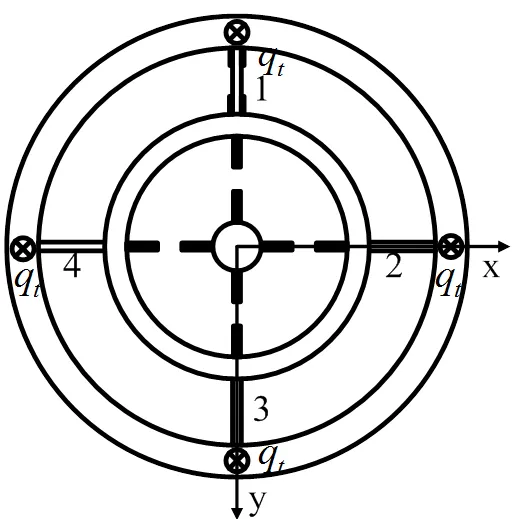
图2 传感器受Fz方向动载

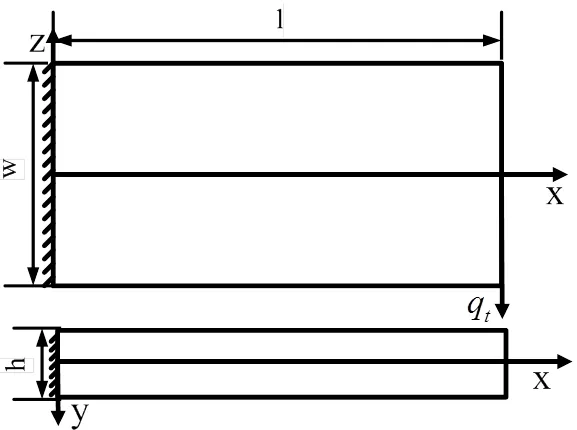
图3 矩形梁受Fz方向动载

图4 传感器受Fx方向动载

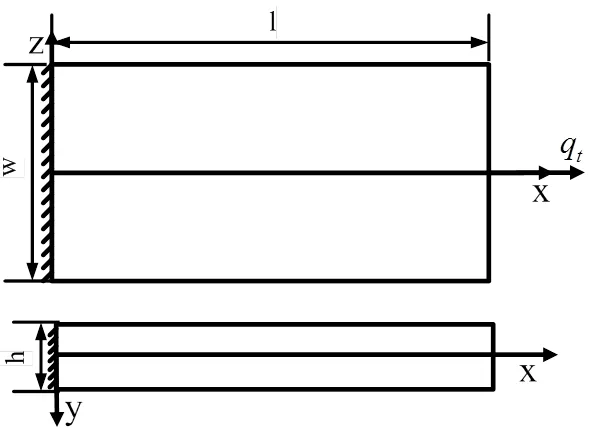
图5 矩形梁受Fx方向动载

2 六维力传感器弹性体强迫振动分析

2.1 矩形梁横向强迫振动分析

根据梁的横向自由振动方程，对梁的主振动进行假设，推导得到梁的主振动：

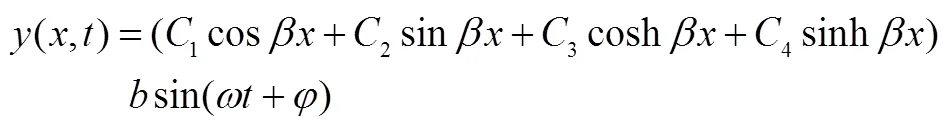
定义（1）式中

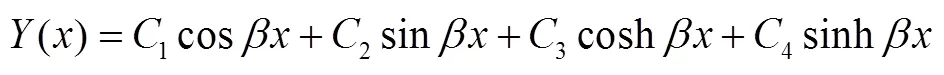
为振型函数。根据传感器中矩形梁横向强迫振动的实际情况，假设梁零初始条件下的响应：

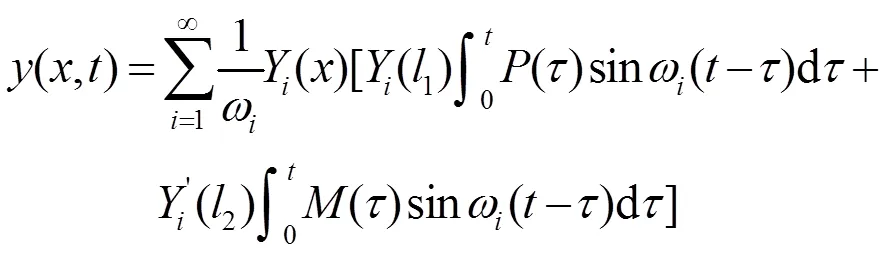
2.2 杆纵向强迫振动分析

根据达朗贝尔原理，推导出杆的纵向强迫振动方程。设方程中纵向动载荷为零，得杆纵向自由振动方程，由此推导出等直杆的主振动：

定义（4）式中

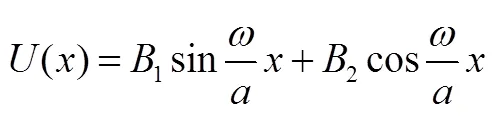
为振型函数。根据杆第i阶正则坐标方程解的假设，以及传感器中矩形弹性体1纵向强迫振动的实际情况，假设杆零初始条件下的响应：

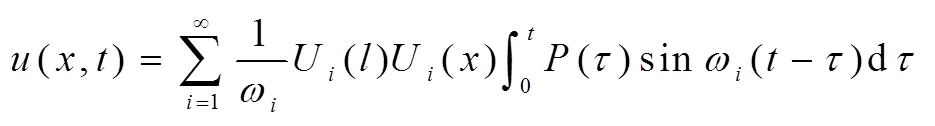
3 算例

3.1 矩形梁横向强迫振动算例

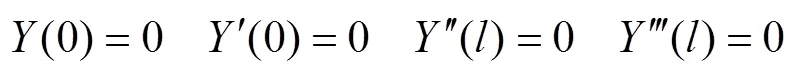
将（7）式代入（2）式，得：C3=-C1，C4=-C2以及βl，如表2所示。

根据固有频率公式：

代入各数值，可以求出前3阶固有频率，见表2。

又由C3=-C1，C4=-C2将（2）式改写成：

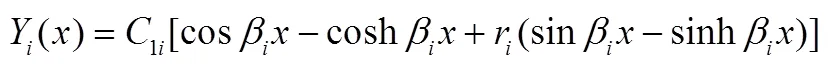
根据主阵型正交性归一化条件：

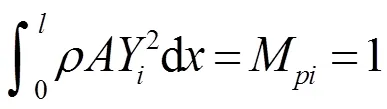
求解出1i，并将1i、β代入（9）式得前三阶振型函数Y()，代入杆长l得Y(1)，以上求解出的各个参数值见表2。

表2 梁横向振动前3阶固有频率及振型函数

根据动载荷Fz、Mx作用时梁横向强迫振动的力学模型假设，作用在梁上的是单一集中载荷，且没有集中力偶矩作用，由(3)式得梁的动态响应为：

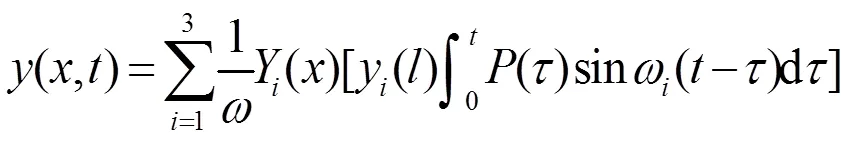
本文假设作用在梁边界上动载荷的表达式为：q=sin(-l)，为动载荷的幅值，()为狄拉克函数。那么，（11）式中的集中力()满足：q=sin(-l)=()(-l)。

借助MATLAB软件，将上面计算出的各个参数代入公式（11），得到梁零初始条件下的动态响应为：

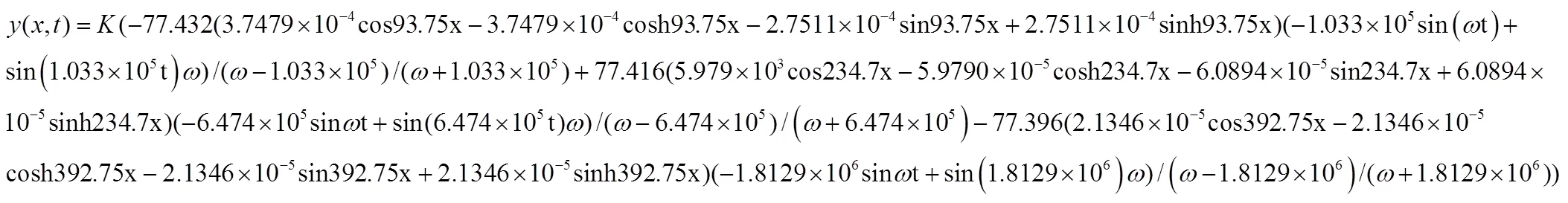
参照薄板假设理论，本文只考虑εx、εy、γxy。根据伯努利-欧拉梁的假设：梁的各截面的中心主惯性轴在同一平面xoz内，外载荷也作用在该平面内，梁在该平面内作横向振动，所以εy=0，此时梁的主要变形是弯曲变形。因为τxy=0(垂直于x轴沿y轴方向的切应力)所以由物理方程得γxy=2(1+μ)τxy/E=0。所以εx就是梁横向强迫振动的输出。

根据空间问题几何方程我们推导出响应与应变之间的关系式只与位置变量x有关：

由于电阻应变片居中贴在弹性体表面，式（12）中取/2，同理借助MATLAB软件，我们得到方向线应变：

在ε中取系数=1。根据工程中机械手动态力带宽实际范围，绘制出激励频率2kHz-4kHz梁的横向强迫振动沿x方向线应变的动态曲面图（图6）：

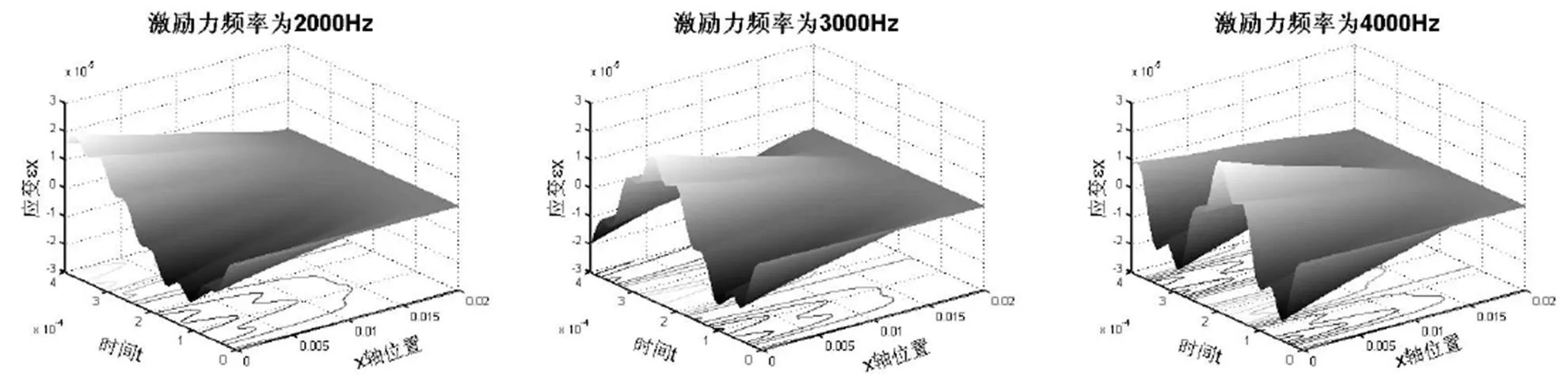
图6 横向振动动态应变

3.2 杆的纵向强迫振动算例

根据Fy作用时矩形截面杆纵向强迫振动的受力分析，如图5所示，将弹性体矩形梁简化为左端固支、右端自由的等直杆，满足简单边界条件假设：

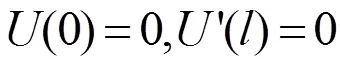
将边界条件（13）代入（5）式求解出固有频率公式和主振型公式：

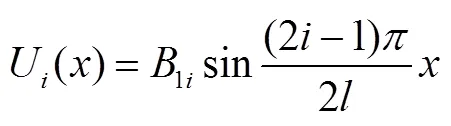
将各参数值代入式（14），可以求出前3阶固有频率ω。

根据主振型正交性归一化条件：

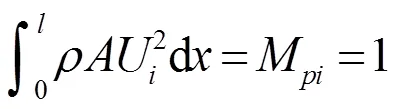
求解出li，并将li代入（15）式得前三阶振型函数U()，代入杆长得U()，以上求解出的各参数值见表3。

表3 杆纵向振动前3阶固有频率及振型函数

同理，假设作用在梁边界上动载荷的表达式为：q=sin(-l)，所以（6）式中的集中力()满足：()=sin。借助MATLAB软件，将上面计算出的各个参数代入公式（6），得到杆零初始条件下的动态响应：

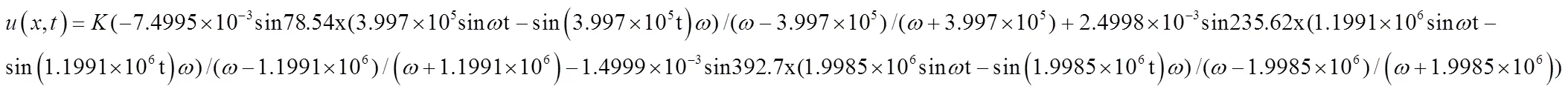
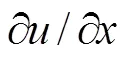
与梁的横向强迫振动同理，εy=0γxy=0。

所以，弹性体沿x轴方向的应变εx就是杆纵向强迫振动的输出。同理，在εx中取系数=1时，绘制出激励频率2kHz-4kHz下杆的纵向强迫振动沿方向线应变的动态曲面图（图7）：

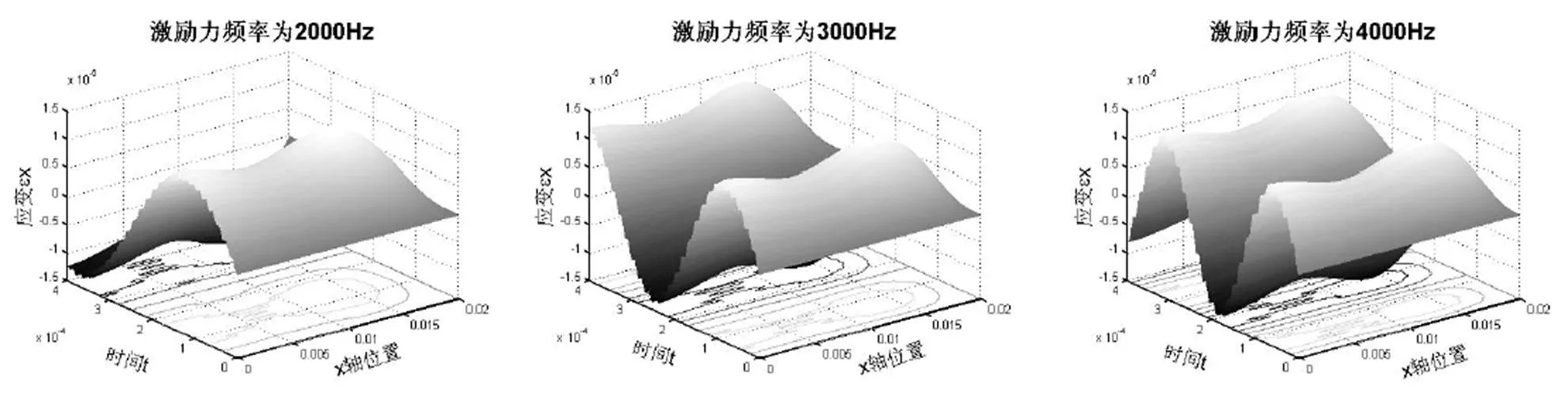
图7 纵向振动动态应变

4 矩形梁模态分析

通过矩形梁的模态分析，得出其固有频率的数值解，可以对解析解的结果进行论证，具有十分重要的意义。根据表1中矩形梁的材料和尺寸参数，并考虑到解耦精度和计算量，通过ANSYS有限元分析软件得出矩形梁的前三阶固有频率如图8所示。

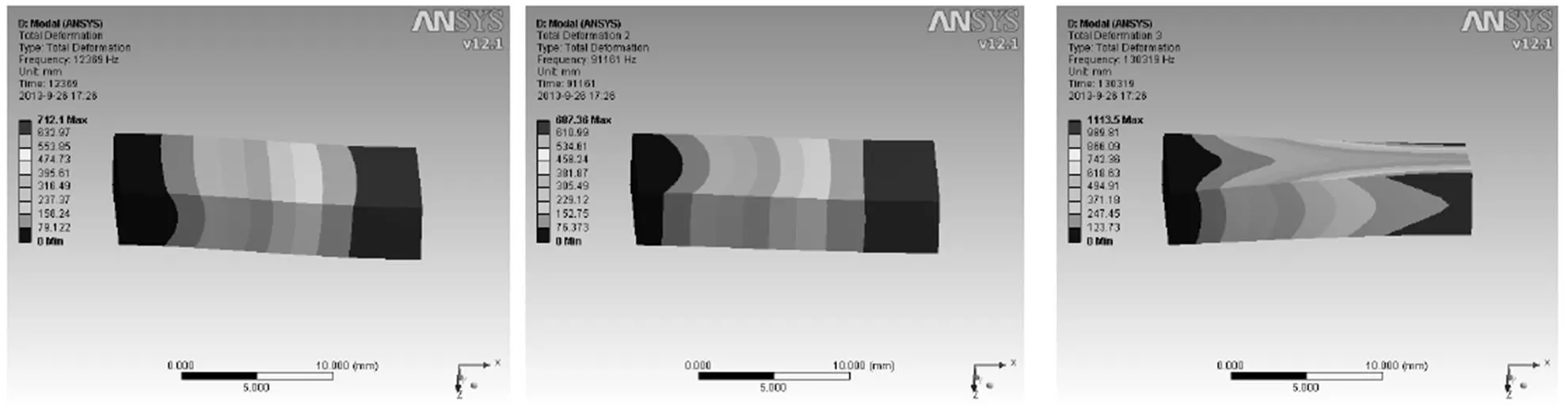
图8 矩形梁前3阶振型数值仿真

理论上，通过压电陶瓷激振器激励传感器弹性体，输出信号频域响应曲线的第一个峰值就是弹性体的一阶固有频率，后面几个峰是高阶固有频率。而实验测得的数据很小，是由于现有压电陶瓷激振器工作频率的极限只能达到1000 Hz，实验时所观测到的峰有可能是噪声信号所致，在无法观测到更高频率峰值的情况下，实验方法不能确认六维力传感器弹性体的固有频率。因此，现阶段实验手段提取六维力传感器动态特征有很大的局限性。

表4 固有频率的三种解（单位：Hz）

5 结论

综合上述分析，本文提出的解析法避开了现有实验手段的局限性，基于弹性力学、振动力学理论，适当简化弹性体结构和边界条件，建立力学模型，提取动态耦合特征，求解过程为动态解耦提供了理论基础。

本文以测量Mz方向力矩的弹性体矩形梁为例，从动力学角度分析了耦合产生的根本原因，求解出了前三阶固有频率、振型函数以及动态输出，并根据传感器的工作带宽，进行了仿真，为六维力传感器动态解耦提供了数据基础。

[1] 许德章,吴仲城,葛运建,等.机器人六维腕力传感器耦合矩阵的确定与摄动分析[J].仪器仪表学报,2005,26(1): 75-81.

[2] 姚智慧,张付祥.机器人六维力传感器研究概况及发展预测[J].广东自动化与信息工程,2002(3):7-9.

[3] 徐科军,周胜生.多维腕力传感器动态特性的频域研究[J].电子测量与仪器学报,1997(2):58-63.

[4] 徐科军,李成.多维力传感器迭代动态解耦方法[J].中国机械工程,1999,10(1):46-48.

[5] 宋国民,张为公,翟羽健.基于对角优势化补偿的传感器动态解耦研究[J].仪器仪表学报,2001,22(4):165-167.

[6] 丁明理, 梁宏, 王祁, 等. 基于小生境遗传算法的多维力传感器动态解耦方法[J]. 传感技术学报, 2006, 19(3): 667-671.

[7] Liu Z S, Wang Y, Chen E W, et al. A method for measuring dynamic performance index of robots multi-axis wrist force sensor[C].Proc. IEEE Int. Conf. on Information Acquisition. Hong Kong and Macau, China: 2005: 170-176.

[8] 倪振华.振动力学[M].西安:西安交通大学出版社,1986: 338-388.

[9] 汪志红.电阻应变片式六维力传感器弹性体力学特性的研究[D].芜湖:安徽工程大学,2013.

[10] Liang Q K, Zhang D, Song Q J, et al. Design and fabrication of a six-dimensional wrist force/torque sensor based on E-type membranes compared to cross beams [J]. Measurement, 2010(43): 1702-1719.

Forced Vibration Analysis of Rectangular Beam of Six-Axis Force Sensor Based on Double Layer E-type Membrane

*XIE Li-feng1, 2, XU De-zhang1, 2

（1.School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu, Anhui 241000, China; 2.Advanced Numerical & Servo Technology, Anhui Polytechnic University, Wuhu, Anhui 241000, China）

Elastic body of six-axis force sensor used to adopt the structure of composite beam. Signal of each splitter direction inevitable contains the coupling-out of forced signal from the other splitter directions. Under the condition of dynamic loads, dynamic coupling-out of six-axis force sensor is very complicated. To reveal the main characteristic of dynamic coupling-out which six-axis force sensor indicates in theory, we study the rectangular beam of six-axis force sensor based on double layer E-type membrane, establish the mechanical models, use the basic theory of elastic mechanics and d'alembert's principle, adopt the first three order modal shapes of the rectangular beam and deduce the dynamic coupling-out which the other five splitter directions act on Mzwhich is the main direction. Finally, figures of dynamic strain will be plotted and the theoreticalbasis for dynamic decoupling of six-axis force sensor has been provided.

six-axis force sensor; coupling; rectangular beam; theory of elastic mechanics; strain

O326

A

10.3969/j.issn.1674-8085.2014.02.013

1674-8085(2014)02-0061-06

2013-09-26；

2014-01-30

国家自然科学基金项目(51175001)；安徽省自然科学基金项目(11040606M144)

*谢黎峰(1988-)，男，安徽芜湖人，硕士生，主要从事机器人与信息感知研究(E-mail:304246668@qq.com)；

许德章(1964-)，男，安徽芜湖人，教授，博士，硕士生导师，主要从事机器人感知研究(E-mail:xdz@ahpu.edu.cn).