Hilbert空间中的一类集值变分包含
罗 静,隆建军
Hilbert空间中的一类集值变分包含
*罗 静1,隆建军2
(1.四川理工学院理学院,四川,自贡 643000;2.攀枝花市大河中学,四川,攀枝花 617061)
讨论了在广义极大单调意义下的一类变分包含,并且使用预解算子技巧研究这类变分包含解的迭代逼近.改进和推广了近期文献中的相关结果。
变分包含;单调映象;预解算子;迭代算法;收敛性
1 预备知识
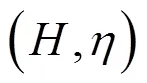
考虑如下变分包含问题:


此问题正是文献[6]研究的问题。
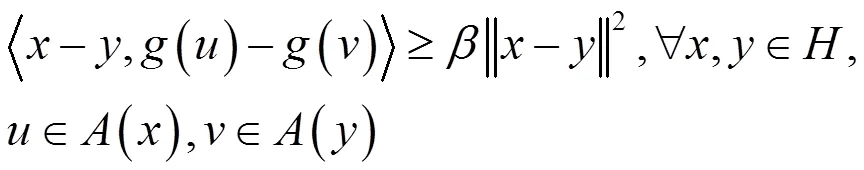
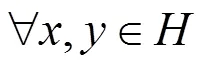
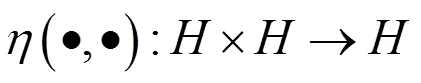
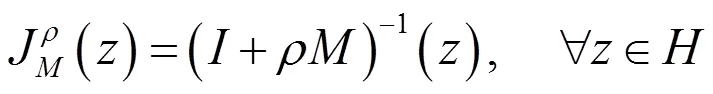
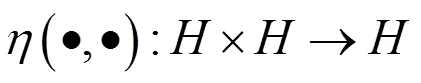
由引理1.1和引理1.2容易得到


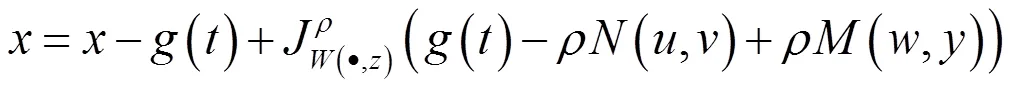
利用(3)式即Nadler[9]的结果,我们能够构造针对变分包含问题(1)解的迭代算法:
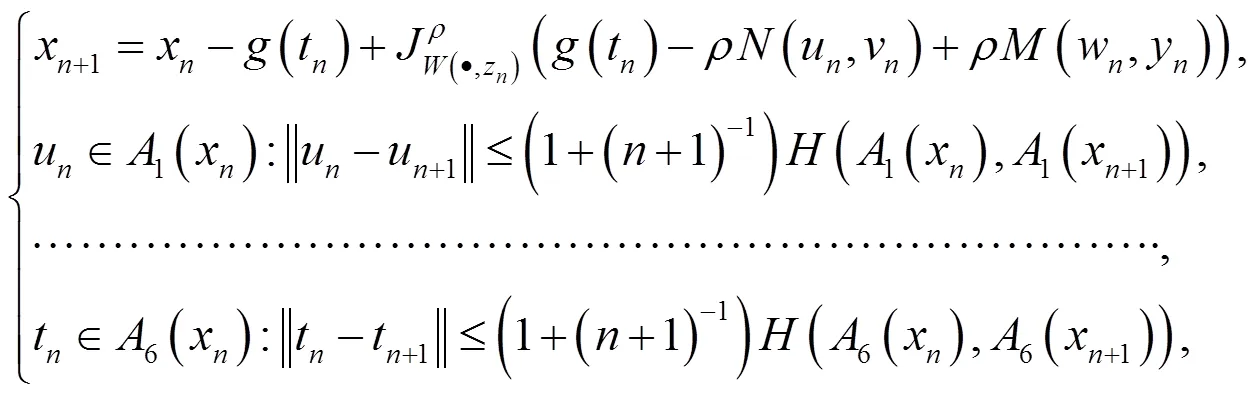
2 主要定理及解的迭代
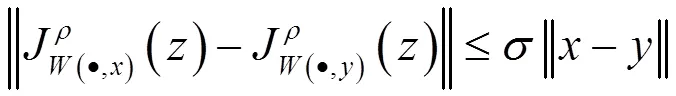
4.1 在青贮发酵后的5 d时,各比例混合青贮的pH值下降速度较快,达到了5. 5左右;发酵的5~35 d期间,青贮pH下降速度缓慢;在55 d时,0%的甜高粱混贮pH最大,其它比例混合青贮基本降到了4. 2左右。


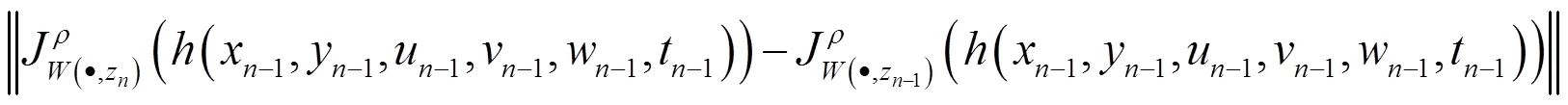

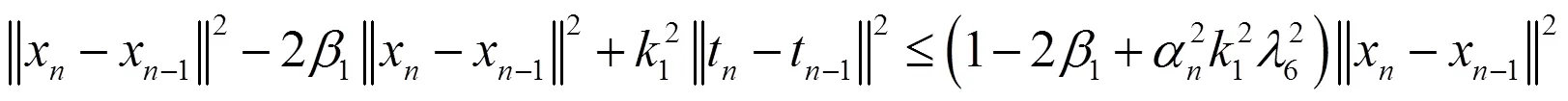
由引理1.2和条件(5),有
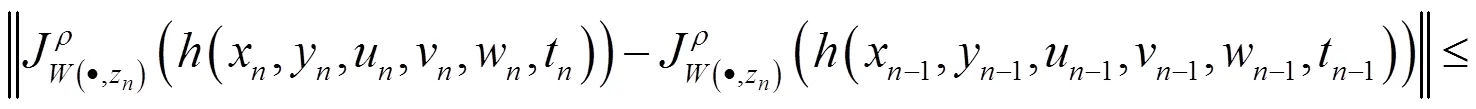

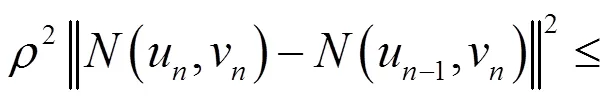

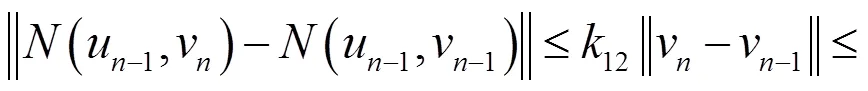
(12)


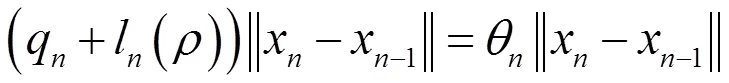
其中
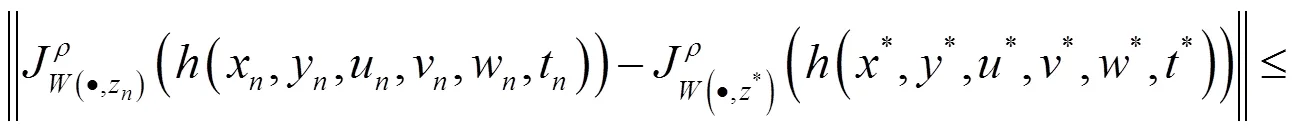
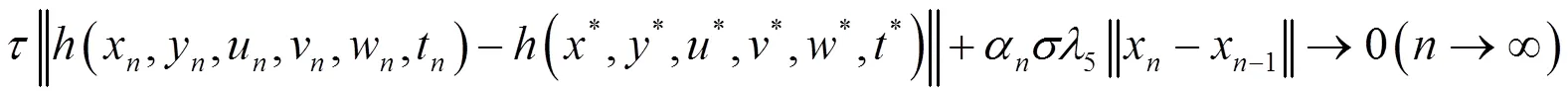
由(4)和(15)式有
即有
注3定理2.1推广和改善了Huang[7],代宏霞[11]等人的工作。
[1] Noor M A. New approximation schemes for general variational inequalities[J]. J Math Anal Appl, 2000, 251: 217-229.
[2] Noor M A. Huang Zhenyu. Three-step methods for nonexpansive mappings and variational inequalities[J]. Appl Math Cornput, 2007, 187: 680-685.
[3] Ding Xieping.Predictor-corrector iterative algorithms for solving nonlinear mixed variational-like inequalities[J].四川师范大学学报:自然科学版,2003,26(1):1-5.
[4] 贡玉军,何中全,牛森.一类广义非线性多值变分包含的迭代算法[J].广西师范大学学报:自然科学版,2008, 25(2):16-20.
[5] 周光辉.一类新的广义集值变分包含问题解的辅助序列迭代算法[J].应用数学,2007,20(3):598-603.
[6] Xia F Q,Huang N J.Variational inclusions with a general H-monotone operator in Banach spaces[J].Comput Math Appl,2007,54:2-30.
[7] Huang N J,Fang Y P.A new class of general variational inclusions involving maximalη-monotone mappings[J]. Publ.Math.Debrecen,2003,62:83-98.
[8] 张彦.一类新的变分包含系统[J].内江师范学院学报,2012,27(1):8-10.
[9] Nadler S B Jr.Multi-valued contraction mappings[J]. Pacific J.Math,1969,38:475-488.
[10] Noor M A. An iterative scheme for a class of quasivariational inequalities[J].J.Math.Anal.Appl,1985, 110:462-468.
[11] 代宏霞.极大η-单调映象的广义隐拟变分包含[J].四川大学学报:自然科学版,2006,43(1):11-15.
A Class of Set-valued Variational Inclusions in Hilbert Spaces
*LUO Jing1,LONG Jian-jun2
(1.School of Science,Sichuan University of Science&Engineering,Zigong, Sichuan 643000,China; 2.Dahe Middle School of Panzhihua, Panzhihua, Sichuan 617061,China)
By using some properties of generalized maximal monotonicty mapping and the resolvent operator technique, in Hilbert space,the author studied a class of variational inclusions with generalized maximal monotonicty mapping and constructed an algorithm for approximating the solution of this class of variational inclusions with generalized maximal monotonicty mapping.
variational inclusions;monotone mapping; resolvent operator; algorithm;convergence
O177.91
A
10.3969/j.issn.1674-8085.2014.02.003
1674-8085(2014)02-0014-05
2013-12-02;
2013-12-26
*罗 静(1980-),女,四川自贡人,助教,主要从事数学分析与复变函数理论方面研究(E-mail: 379040763@qq.com);
隆建军(1981-),男,四川安岳人,中学二级教师,主要从事高中数学教学与不等式理论研究(E-mail: longjianjun1234@163.com).

