图像分块压缩感知中的自适应测量率设定方法

李然，干宗良，崔子冠，武明虎，朱秀昌

(南京邮电大学 江苏省图像处理与图像通信重点实验室，江苏 南京 210003)

1 引言

传统的图像采样以奈奎斯特(Nyquist)采样定理为理论基础，要求采样速率至少为图像带宽的2倍。高采样率不仅导致了图像采集设备需要集成大量的传感器，而且也使采集数据所占用的存储空间较大，不得不引入一定计算量去压缩图像数据。高成本、高能耗和高计算复杂度使传统图像采集设备十分不适合应用到要求“轻负担”采集点的场合，如计算能力、内存容量和耗电量都受限的无线传感器网络终端。近年来，压缩感知(CS,compressed sensing)的出现突破了奈奎斯特采样定理的瓶颈[1,2]，使以欠奈奎斯特速率采样信号仍可无失真复原信号。基于CS的图像采集即压缩成像(CI,compressive imaging)也随之出现[3～5]，实现了在模拟域中采集图像的同时以降维的方式直接压缩图像，大大降低了采集图像成本，使之获得广泛关注。

图像压缩感知目前面临着若干难题，主要包括计算负担大的重构过程和高存储量的随机测量矩阵。然而，在图像压缩感知的应用场合中，解码端经常是计算能力强大的基站，这使高计算复杂度的重构算法仍可“轻松”完成。但是，由于图像规模较大(成百上千万像素)，造成随机测量矩阵的存储量庞大，这不仅给图像重构带来困难，而且也使CI设备实现随机测量耗费的代价过大(高延迟、高成本等[6])。为了减少随机测量的代价，文献[7]提出了分块压缩感知(BCS,block CS)，该框架运用相同的测量矩阵对每一个图像块进行测量。由于分块尺寸较小，存储测量矩阵所需空间和计算复杂度均会大大较低，这使基于分块的 CI设备更符合工程实际且易于实现。但是分块方法也存在很大缺陷，主要是因为每个图像块具有相同的测量率，这样就忽略了各个块具有不同特征的实际，即获得相同的复原质量，细节复杂的块需要做较多的测量，细节简单的块则需要做较少的测量。为了克服该缺陷，文献[8～10]均提出利用图像块方差度量细节复杂度为各块设定不同的测量率，从而有效地捕获图像信息，改善图像重构质量。但是，为了计算图像块方差，需要首先获得原始数字图像，这严重背离了CS采集的同时直接压缩图像的基本精神，且实际的 CI设备是直接采集模拟图像，所以在采集点获得原始数字图像是不现实的。那么，利用在采集端可得的CS测量值自适应地调整各块的测量率，才是一种更为现实的方案。

针对图像分块压缩感知中自适应设定各块测量率需要利用原始数字图像的缺陷，提出了一种更符合于工程实际的自适应测量率设定方法。该方法直接利用采集端可得的测量值计算各图像块方差，再根据各块方差自适应地调整测量率。为了满足预设的图像总测量率，也提出了动态设定块测量率的方案。仿真实验结果表明，本文所提出方法能够有效地消除块效应，改善了重构图像质量，且优于使用固定测量率的方法。

2 图像的自适应分块压缩感知

在分块压缩感知的基础上，文献[8]提出了自适应分块压缩感知(ABCS,adaptive block CS)框架。在该框架下，首先将N=Ic×Ir个像素的图像x分成n个大小为B×B的块，第i个块的列向量形式记为xi(i=1,…,n,n=N/B2)，然后，根据块方差为每块确定不同的测量次数Mi，生成相应的随机测量矩阵ΦBi，按式(1)得到每块的测量值yi

且定义各块的测量率Ri如下

由于具有高方差的图像块往往包含的边缘或纹理成份较大，所以它们需要更多的测量值才能较好地复原，然而，低方差块一般是具有简单细节的平滑块，则需要较少的测量值。通过自适应分配各块测量次数，可平衡各块的复原水平，从而有效地减少块效应，改善图像重构质量。对于随机测量矩阵 ΦBi，一般使用理论上最优的高斯随机矩阵[11]，但其并不易通过硬件实现。为了增加测量矩阵的硬件友好度，文献[12]所提出的结构化随机哈达玛矩阵(SRHM,structural random Hadamard matrix)也可被引入到ABCS框架中。

3 所提出的自适应测量率设定方法

在ABCS框架中，为了计算图像块方差，采集端需要获得原始数字图像，也就是首先利用传统的图像采集设备将模拟图像转化为数字图像；接着在像素域中计算各块方差，并根据方差自适应确定测量次数和生成相应的测量矩阵；最后，对各块进行随机下采样完成压缩。这一过程实际上仍是先采集后压缩，并未体现CS采集的同时压缩的特点。另外，在实际的工程应用中，采集端由CI设备构成，其直接将模拟图像通过随机下采样得到已压缩的测量值，所以原始数字图像在采集端被利用是不现实的。最现实的做法是仅利用测量值判断图像块的细节复杂度以自适应地设定各块的测量率。在本文中，利用随机测量矩阵的统计特性，图像块方差的计算由像素域转移到测量域中进行，如此就避免了在采集端对原始数字图像的依赖，从而使自适应设定测量率更易于与CI设备融合。

3.1 测量域中图像块方差的计算

在像素域中，图像块 xi的样本均值可由式(3)计算

那么，其样本方差为

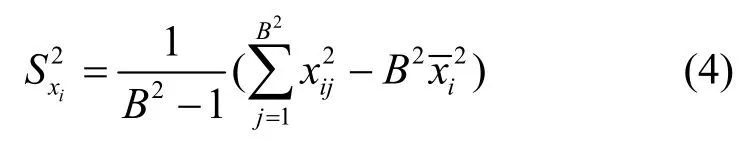
为了理论推导方便，随机测量矩阵选用大小为Mi×B2高斯随机矩阵ΦBi，其中，每个分量φmj均相互独立地服从均值为0和方差为1/Mi的高斯分布，则测量值向量yi中的每个分量可表示为

即 yim由B2个高斯变量 φmj线性组合而成，可知其仍服从高斯分布，且均值和方差分别为

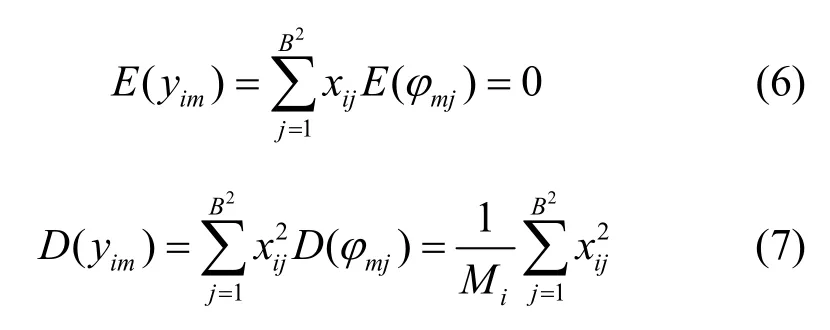
结合式(3)、式(4)和式(7)，可得

那么，将测量值向量yi看作是一个服从均值为0和方差为D(yim)高斯分布的总体，yim(m=1,…,Mi)看作是该总体的Mi个随机样本，则D(yim)的无偏估计量为yi的样本方差，即

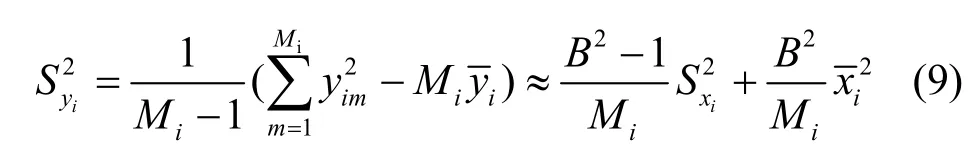
因此，由式(9)可得图像块xi的样本方差估计为

由式(10)可看出，图像块的样本方差可用其相应的测量值和均值估计。由于在实际的CI设备中，图像块样本均值可当作是一个CS测量值，那么图像块样本方差的计算就完全能在测量域中进行。当然，在测量域中估计得到的块样本方差与真实的样本方差仍然存在一定偏差，所以块样本方差估计很有可能出现负值，为了防止负值的出现，式(10)改进为

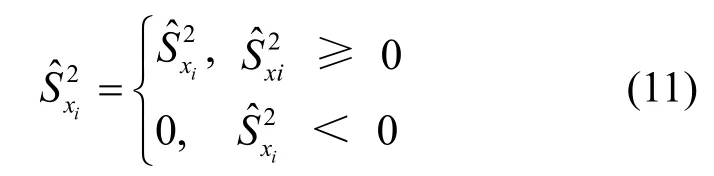
因为需要根据图像中所有块方差的大小进行测量次数分配，所以为了能够突出体现各块方差大小，对估计得到的图像块方差进行规范化如下

图1显示了对于分块尺寸 B=32的 512×512 Lenna图像，当每块测量次数分别取512、64和16时，测量域计算的各块样本方差估计值与像素域计算的块样本方差真实值之间的误差能量。由图1(a)可看出测量次数较高时，在测量域计算出的各块样本方差与真实值之间的误差基本为0，但随着测量次数降低，由于样本数急剧减少，块样本方差估计值与真实值的误差逐渐明显。因此，为了确保样本方差估计值的准确性，应尽量取较大的测量次数。

在上述推导过程中，采用了高斯随机矩阵作为测量矩阵。然而，高斯随机矩阵的各分量取值是连续的，并不易通过硬件实现。SRHM矩阵的各分量取值仅有2种可能：−1和+1，所以十分容易通过硬件实现，且其与高斯随机矩阵相似，与任意固定矩阵都高度不相干，同样可实现接近理论最优的重构性能。那么，当测量矩阵使用SRHM矩阵时，式(10)是否仍可用于去估计图像块样本方差。选取5幅512×512 图像：Lenna、Barbara、Peppers、Mandrill和Goldhill，采用SRHM矩阵对它们所有的图像块(分块尺寸分别为32×32和16×16)进行随机测量，生成测量值的统计分布如图2所示，可看出在不同测量率下，测量值的统计分布均以0为中心近似对称，那么可知测量值的均值E(yim)近似为0。

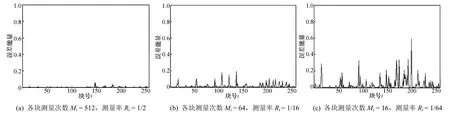
图1 测量矩阵为高斯随机矩阵时，不同测量率下512×512 Lenna图像(B=32)的各块样本方差估计值与真实值之间的误差能量

图2 图像块的测量值统计分布

虽然对于测量值的方差是未知的，但根据SRHM 矩阵的受限等距性(RIP,restricted isometry property)，测量向量yi的能量应与相应的图像块xi的能量近似相等，所以可建立式(15)。

这里，也将图像块各像素取值看作是随机变量。同样，分别使用样本均值和样本方差代替统计均值和统计方差，得

其中，c1和c2为常数。需要说明的是，c1和c2的引入是为了补偿一定能量，由于随机下采样总是会损失能量，所以可通过设置系数适当地放大能量，使式(16)两端尽量保持相等。根据经验，当 c1取(B2−1)/Mi，c2取 B2/Mi时，可获得较好的效果。通过式(9)，也可看出c1、c2取上述经验值时，块样本方差估计值仍可使用式(10)计算。对于分块尺寸B=32的512×512 Lenna图像，测量矩阵采用SRHM矩阵，使用式(10)在测量域估计块样本方差，当每块测量次数分别取512、64和16时，计算各块样本方差估计值与真实值之间的误差能量，如图3所示。可看出，与高斯随机矩阵相似，当测量次数较高时，在测量域中计算的块样本方差估计值十分逼近于真实值，但随着测量次数的降低，它们之间的误差逐渐地增大。因此，SRHM矩阵也需要取较大的测量次数，才能确保样本方差估计值的准确性。

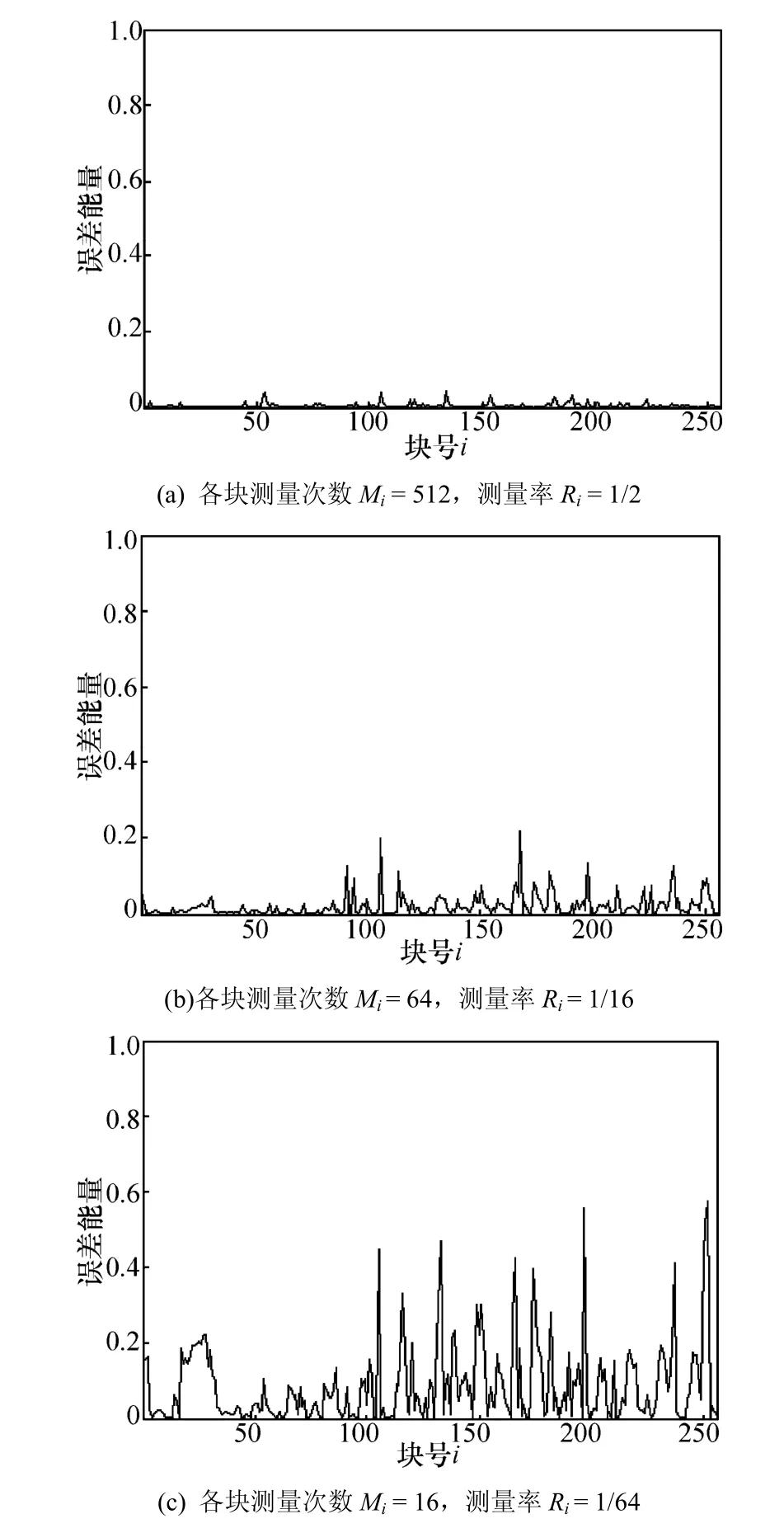
图3 测量矩阵为SRHM矩阵时，不同测量率下512×512 Lenna图像(B=32)的各块样本方差估计值与真实值之间的误差能量

综上可知，无论使用高斯随机矩阵，还是使用硬件友好度高的SRHM矩阵，均可使用式(10)在测量域中估计各图像块方差。那么，利用该结论就可直接在测量域中根据图像块方差自适应地为各块设定适当的测量率。

3.2 基于图像块方差的自适应测量率设定法

尽管图像块方差的计算可转移到测量域进行，但如何利用方差为各块合理地设定测量率，也十分重要。自适应设定测量率的方案不仅要能够容易通过 CI设备实现，而且也要尽量克服低测量率方差估计值偏差大的缺陷。另外，考虑到传输信道容量和图像统计特性变化问题，该方案也应该较容易实现码率控制，即可提前预设图像总测量率，使总测量率不随图像的变化而变。假设预设的图像总测量率为R，可知总测量次数M=RN，为各块自适应设定测量率的步骤如下。

步骤1 首先对各图像块xi作预测量，得到Mpi个预测量值，再利用它们根据式(10)估计出规范化的图像块样本方差di。由于测量次数较低将导致估计出的块样本方差值与真实值之间的误差较大，所以应取较大的预测量次数Mpi。

步骤2 预先给每块分配测量次数M0i

步骤3 利用每块的样本方差占所有块样本方差总和的比例，根据式(18)计算出每块的测量次数Mi

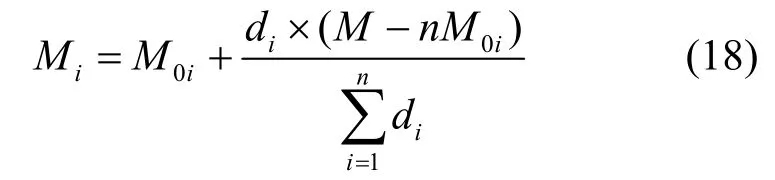
步骤4 设定块的测量次数上界为upper=0.9B2，找出超出上界的块，将其测量次数限定为upper，随后将剩余的测量次数均匀地分配给未越界的块，再次分配后可能又会出现越界的块，那么重复上述操作，直到所有块均不越界为止。如此就可得到最终的各块测量次数Mi。

步骤5 根据为各块重新分配的测量次数，在由步骤1已获得的预测量值的基础上，对需要补充测量的块，利用 CI设备再次进行测量以满足该块所需的测量次数；对有过多测量的块，则直接删去多余的测量值。

通过上述过程后，各块的测量值将会传输到解码端，再利用适当的 CS重构算法对图像各块进行重构。另外，本文所提出的自适应测量率设定方案的计算复杂度为O(nMpiB2+ nB2+2n)，其与预测量次数 Mpi成正比关系。为了保证样本方差的准确性，Mpi的取值往往较大，所以，较传统的图像分块压缩感知模型，本文方案会增加一定的计算复杂度。

4 实验结果与分析

为了测试本文所提出的自适应测量率设定方法，使用以下2种方法与之相比较：(1)各图像块均作固定测量率的CS测量(非自适应)[7]；(2)用像素域中计算各块样本方差的真实值代替测量域中计算的估计值，再按照本文方案的步骤2至步骤5自适应地为每块设定测量率(像素域自适应)。重构时使用GPSR算法[13]独立地重构出各图像块，稀疏基底使用Daubechies-4正交小波。采用3幅512×512 灰度图像(Lenna、Barbara和 Mandrill)测试上述3种方案，分块尺寸B=32，预设的图像总测量率分别取0.1到0.5。由于测量矩阵具有随机性，每种方案下重构图像的PSNR值均取5次测试的平均值。

表1显示了测量矩阵为高斯随机矩阵，且预测量次数Mpi取512时，各方案下重构图像的PSNR值对比。从表中可看出，与非自适应测量相比，自适应设定测量率可有效地改善重构图像的客观质量。然而，像素域自适应方案获得PSNR值的增益是略高于本文方案的，这是因为测量域估计的块样本方差与真实值存在一些偏差，对各块测量次数的分配造成了影响。对于细节纹理较简单的Lenna图，无论在低测量率还是高测量率下，本文方案获得的PSNR增益均在1 dB左右，这是因为预设的图像总测量次数经过自适应调整后，各块的测量次数均能保证良好的重构质量；对于细节纹理较复杂的Barbara、Mandrill图，PSNR增益将随着预设的总测量率升高而升高，这是因为图像的纹理越复杂，为了保证良好的重构质量，各块需要的测量次数也越多，总测量次数过低，即便经过自适应分配，部分块仍然无法获得充足的测量次数，从而导致PSNR增益不显著，但随着总测量次数的升高，各块逐渐均能确保充足的测量，因此PSNR增益也逐渐升高。图4也展示了在测量率为0.3时，各方案重构出Lenna图像的主观视觉质量对比，可看出与非自适应方案比较，像素域自适应方案与本文方案均可有效缓解块效应现象，对于纹理较复杂的块(如眼睛区域)，也能很好地消除模糊，获得了良好的主观视觉质量。

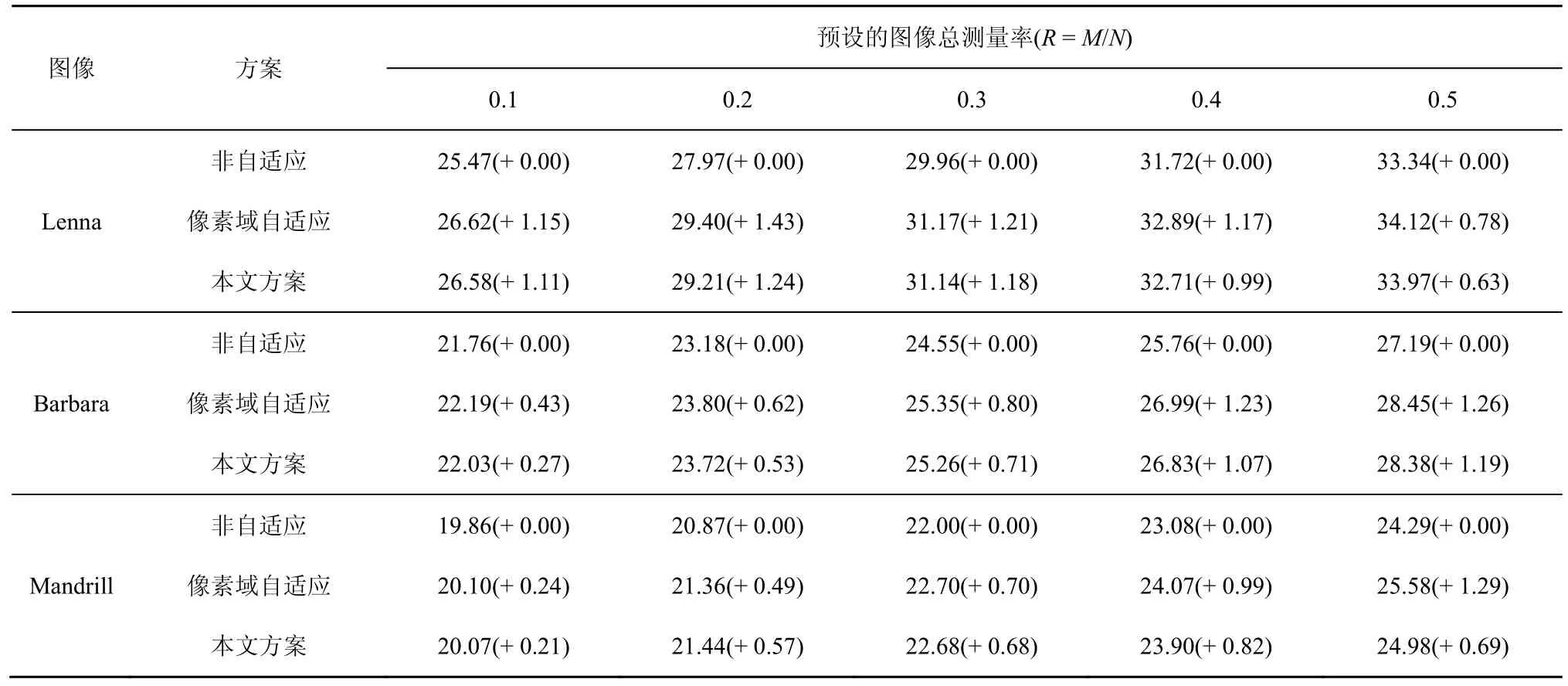
表1 测量矩阵为高斯随机矩阵且预测量次数Mpi取512时，各方案下重构图像的PSNR值/dB

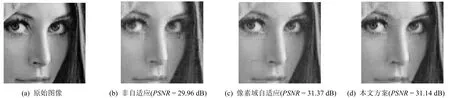
图4 512×512 Lenna图，测量矩阵为高斯随机矩阵，测量率为0.3，各方案重构图像的主观视觉质量对比

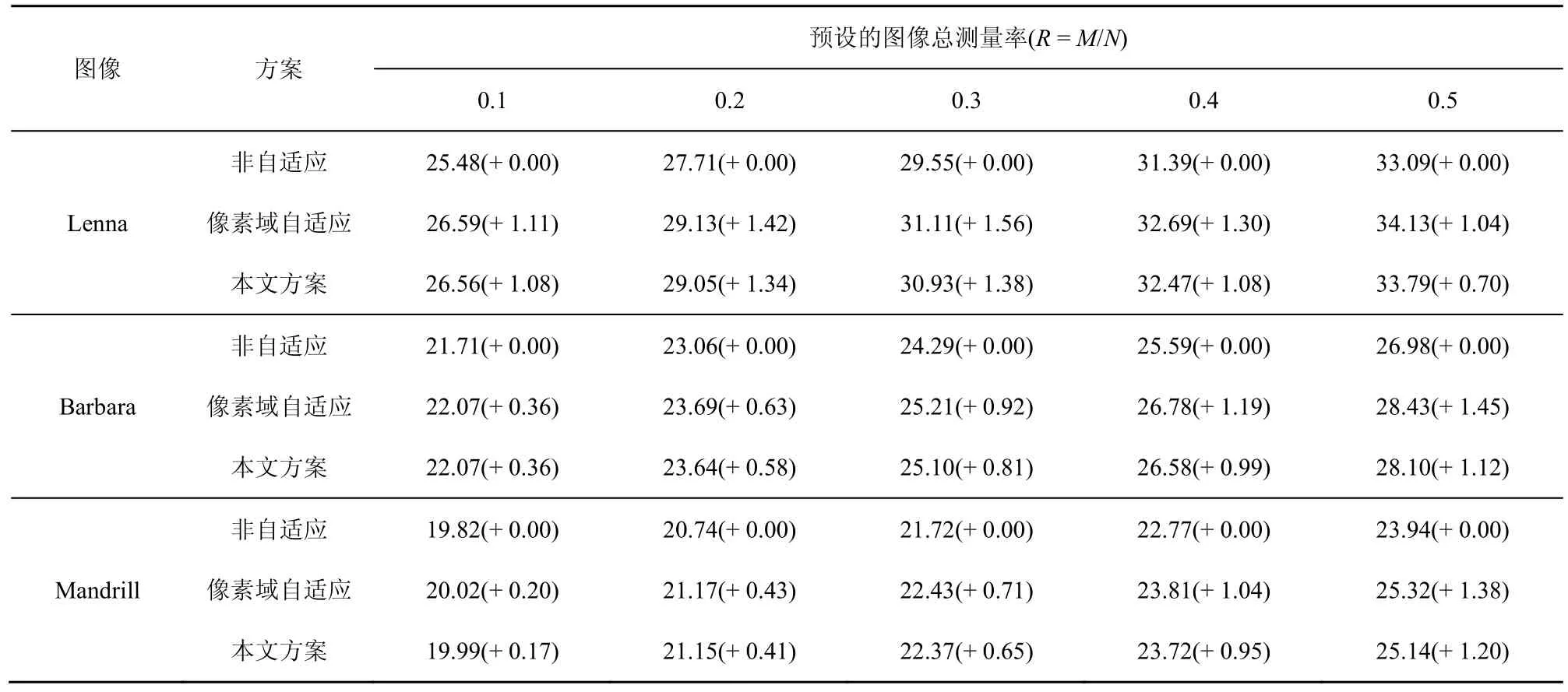
表2 测量矩阵为SRHM矩阵且预测量次数Mpi取512时，各方案下重构图像的PSNR值/dB

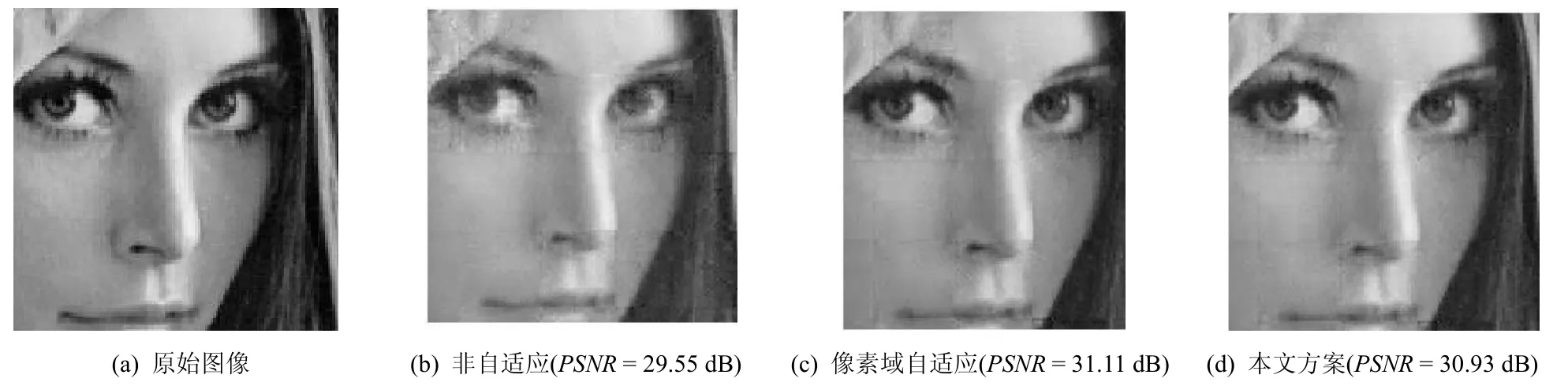
图5 512×512 Lenna图，测量矩阵为SRHM矩阵，测量率为0.3，各方案重构图像的主观视觉质量对比

表2显示了测量矩阵为SRHM矩阵，且预测量次数Mpi取512时，各方案下重构图像的PSNR值对比。与测量矩阵为高斯随机矩阵相似，自适应方案重构图像的客观质量明显高于非自适应方案。在2种自适应方案中，像素域自适应方案由于使用块方差真实值，所以其性能是高于本文方案的。对于细节纹理简单的Lenna图，图像预设的总测量次数不会对本文方案的PSNR增益造成影响，PSNR增益均在1 dB左右；对于细节纹理较复杂的Barbara、Mandrill图，总测量次数过低将导致个别块无法进行充分多的测量，影响了重构质量，但随着总测量次数的升高，该问题可得到有效缓解。由图 5可看出，在测量率为0.3时，本文方案重构出的Lenna图像的主观视觉质量良好，可有效缓解块效应与模糊现象，十分接近于像素域自适应方案重构出的图像。

图6展示了当预测量次数 Mpi降低时，对Lenna图的重构质量所造成的影响。可看出，随着Mpi取值降低，不同测量率下的重构图像PSNR值也不断降低：当Mpi取512时，本文方案的PSNR值基本与像素域自适应方案持平，明显优于非自适应方案；当Mpi取64时，本文方案的PSNR值降低，在低测量率下，略高于非自适应方案，而在高测量率下，略低于非自适应方案；当 Mpi取16时，在不同测量率下，本文方案的PSNR值均劣于非自适应方案。导致这一现象的原因是预测量次数过低导致估计出的块样本方差值与真实值之间的误差较大，从而使本文方案无法准确依靠块样本方差值自适应调整测量率。因此，为了能够确保本文方案的有效性，预测量次数 Mpi取值应充分大，以减少块样本方差估计值与真实值之间的误差。

表3显示了传统图像分块CS模型(即非自适应方案)与本文方案测量512×512 Lenna图所消耗的时间，其中预测量次数 Mpi取 512。实验的硬件平台为主频3.20GHz的酷睿i5 CPU计算机，软件平台为Windows764位操作系统和Matlab 7.6仿真实验软件。可看出，本文方案的测量图像所消耗的时间高于传统分块方案，这是因为预测量环节和自适应测量率分配过程引入一定的计算量。因此，可知重构图像时所获得的PSNR增益是以在采集端增加计算量为代价的。

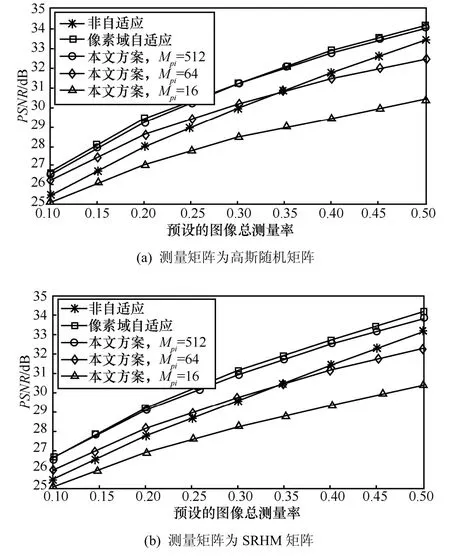
图6 512×512 Lenna图，预测量次数Mpi分别取512、64、16时，不同测量率下本文方案重构图像的PSNR值比较

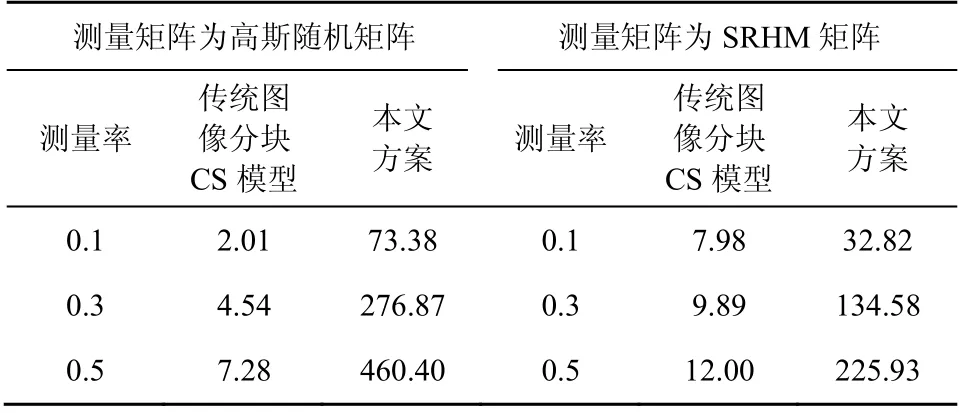
表3 传统图像分块CS模型与本文方案测量512×512 Lenna图所消耗的时间/ms

5 结束语

针对已有的图像分块压缩感知自适应设定测量率方法的缺陷，提出了一种仅利用CS测量值为各图像块自适应分配测量率的方案。该方案并不需要在采集端获得原始数字图像，而是在测量域直接计算块样本方差，再根据各块样本方差作为依据，为每块设定合适的测量率。除此之外，该方案也易于采用硬件实现，且能够灵活地控制其输出码率。仿真实验结果表明，本文方案重构图像的质量优于非自适应方案，但由于测量域计算块样本方案存在偏差，使其与直接利用块样本方差真实值的自适应方案相比，仍具有一定差距。

对于本文所提出的自适应测量率设定法仍有 2方面不足：1)本文重构图像时所获得的PSNR增益是以在采集端增加计算量为代价的，且测量图像所消耗时间显著高于传统分块方案，如何改进所提出方案以缩短测量时间值得进一步的研究；2)块样本方差估计值与真实值之间的误差会随预测量次数降低而增大，分析预测量次数与误差之间的关系以适当地设置预测量次数也值得进一步的研究。

[1]CANDES E,TAO T. Robust uncertainty principle: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory,2006,52(2): 489-509.

[2]DONOHO D L. Compressed sensing[J]. IEEE Trans Inform Theory,2006,52(4): 1289-1306.

[3]DUARTE M F,DAVENPORT M A,TAKHAR D,et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine,2008,25(2): 83-91.

[4]JACQUES L,VANDERGHEYNST P,BIBET A,et al. CMOS compressed imaging by random convolution[A]. Proceedings of the International Conference on Acoustics,Speech and Signal Processing[C].Taipei,China,2009. 1113-1116.

[5]ROBUCCI R,GRAY J D,CHIU L K,et al. Compressive sensing on a CMOS separable-transform image sensor[J]. Proceedings of the IEEE,2010,98(6): 1089-1101.

[6]FOWLER J E,MUN S,ERIC W T. Block-based compressed sensing of images and video[J]. Foudations and Trends in Signal Processing,2012,4(4): 297-416.

[7]GAN L. Block compressed sensing of natural images[A]. Proceedings of the International Conference on Digital Signal Processing[C]. Cardiff,UK,2007. 403-406.

[8]WANG A,LIU L,ZENG B,et al. Progressive image coding based on an adaptive block compressed sensing[J]. IEICE Electronics Express,2011,8(8): 575-581.

[9]SHE Q S,LUO Z Z,ZHU Y P,et al. Spatially adaptive image reconstruction via compressive sensing[A]. Proceedings of the 7th Asian Control Conference[C]. Hong Kong,China,2011.1571-1575.

[10]SUN L Q,WEN X B,LEI M,et al. Signal reconstruction based on block compressed sensing[J]. Artificial Intelligence and Computational Intelligence,2011,7003(1): 312-319.

[11]CANDES E,WAKIN M. An introduction to compressive sampling[J].IEEE Signal Processing Magazine,2008,25(2):21-30.

[12]DO T,GAN L,NGUYEN N,et al. Fast and efficient compressivesensing using structurally random matrices[J]. IEEE Transactions on Signal Processing,2012,60(1):139-154.

[13]FIGUEIREDO M A T,NOWAK R D,WRIGHT S J. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems[J]. IEEE Journal Selected Topics in Signal Processing,2007,1(4):586-597.