基于布尔集线器的线速多播自路由交换结构

尘福兴，李挥，崔凯，张博

（1. 北京大学 深圳研究生院 深圳市云计算关键技术和应用重点实验室，广东 深圳 518055；2. 国家数字交换系统工程技术研究中心，河南 郑州 450002）

1 引言

1984年，Huang和Knauer首次对ATM网络中多播数据的交换问题予以关注，并设计出一种新型交换结构来支持多播，提出了第一个多播交换结构——Starlite[1]。自此，业界对高效的多播结构进行了持续的研究。其中，Saito提出了基于共享存储式的交换结构来实现多播的方法[2]。但是由于存储器带宽的限制使该结构不能够满足大规模扩展需求。Yeh提出了一种基于Knockout理论多播交换结构，每个输入端口采用完全连接的方式连接到输出接口模块[3]。Chao提出了基于该结构的多播设计方案，但是由于文献[3,4]结构的级间采用总线式完全连接方式，所以该结构存在线路器件驱动能力的极限问题，使该类方案在大规模扩展性能上存在瓶颈。

基于 banyan的多播交换结构大多采用多播复制的方法，Lee提出了一种内部无阻塞的复制网络设计方案[5]，由于该方案累加和网络及虚拟地址编码器不适合大规模扩展，会发生满溢(overflow)的现象；多播地址转换所需缓存开销庞大，结构过于复杂，难以满足大规模扩展的需求。文献[6]提出了一种能够为复制网络提供公平机制的方案，然而它进一步增加了结构复制络的复杂性，使其难以应用于大规模的交换结构设计中。

文献[7]提出了一种基于 Clos交换结构多播调度算法，引入了一种路径分配向量，但整个路径决策时间复杂度较高，无法大规模扩展。文献[8]证明了对Clos网络进行多播路径匹配是NP完全问题。

基于Crossbar多播交换结构的研究则大都是关于多播调度算法。Hui和Ali分析了在随机情况下扇出和非扇出交替类的多播调度算法的性能，这些研究都证明了由于信元头阻塞（HOL blocking）会导致吞吐率大大降低[9,10]。Marsan在理论上证明了对于采用虚拟输出队列（VOQ）的大规模多播交换结构，不存在一个有限的提速因子能使许可的多播流量达到100%的吞吐率[11]。Pan提出了一种将信元载荷与目的地址信息分开存储的方案，但其要求的(N+1)(N为输入/输出的端口数)倍于外部链路带宽的加速比，本身就是大规模扩展的瓶颈[12]。

从以上对多播交换结构的研究中可以看出，现有的多播交换结构都无法满足大规模可扩展、线速多播的要求，本文在分配格理论基础上，通过将“统计线组”的技术应用到分治网络中，用合适的集线器来代替该网络中节点，并从理论上对该结构性能证明，从而得到具有低时延、无抖动和无需排队缓存优势以及满足大规模可扩展以及线速多播需求的线速多播交换结构。该结构在一定条件下能很好地解决多播交换结构大规模可扩展以及线速多播问题的同时，又能保证较好的服务质量。

2 多级互联完全分布式自路由模型和布尔多播交换单元

2.1 多级互联分布式自路由模型

多级互连完全分布式自路由模型[13]以分治网络(divide & conquer)[14]为基础，而构建的具有高度模块化，最低的器件复杂度（N lb N）等优点的多播交换结构模型。以N=64[ id:(65):(654):(63)(52)(41): (65): (654): id ]的分治网络为例，如图1所示。其中，“:”表示一级2×2单元，而两级间连线方式用一组位置换群元素表示，如(63)(52)(41)。

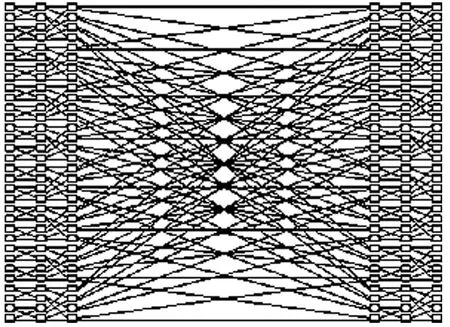
图1 64×64的分治网络

该类网络的自路由特性由其“迹trace”和“导guide”[15]序列共同决定，给出了网络的“迹 trace（TK）”和“导guide(RK)”序列及其自路由过程。对于一个 N×N交换结构，多级互联网络（MIN,multi-stage interconnection network）由于其分布式自路由特性，以及其理想的单元复杂度 Θ(NlbN)，因而适用于构造大规模交换结构。交换结构的艺术就是由最基本的2×2元件通过各种拓扑结构以最低的代价构造出符合性能指标的大型交换系统。理想的结构是其规模可以任意递归扩展，不存在任何瓶颈。因此基于该分布式自路由模型构建多播交换结构模型的理由和动机是充分的、明显的。构建多播交换结构的第一步应该分析分布式自路由模型的基本交换单元及其原理。

图1所示基本单元是由图2(a)～图2(c)状态的自路由排序单元构成，进入该2×2基本自路由排序单元的数据分组排序交换过程可以使用带内信令来实现，例如，在数据分组的前面加上2位带内信令。第一位A1表示当前时隙是否有数据分组，1表示存在有效数据分组，0表示不存在有效数据分组即为空分组；当A1为1时第二位D1表示分组的输出目标端口地址才有意义，否则D1为无效位。故A1D1等于‘10’、‘11’、‘00’、‘01’时分别代表“输出目标端口为0的有效数据分组”，“输出目标端口为1的有效数据分组”，“空分组”，“空分组”。

自路由模型的基本2×2单元（如图2(a)～图2(c)）按如下规定的线性排序关系实现自路由：10＜00＜11，具体控制方式可参见表1。

图2 2×2基本自路由排序单元处于BAR、CROSS、CONFLICT、BICAST的状态

表1中，CONF(CONFLICT)表示冲突，由其他方式比如优先级来决定哪个信号会被输出。

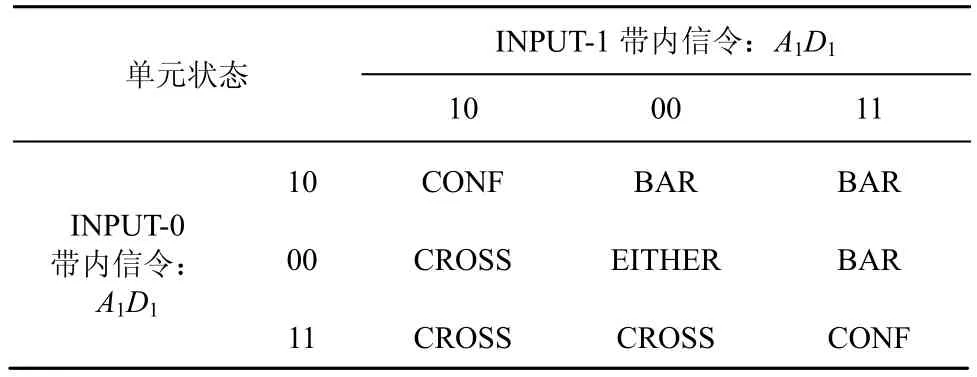
表1 单播2×2基本自路由单元以两位带内信令自路由的交换控制

自路由模型的基本单播2×2单元显然不具备硬件电路拷贝的线速多播特性。为了达到线速多播交换的目的，需要将图2中只有BAR和CROSS 2种单播路由方式的排序单元进行重新定义，使其成为一种全新的满足多播要求的排序交换单元，称为多播交换单元（如图2(d)、图2(e)所示）。基本交换单元在加入BICAST状态后，需要满足何种条件才能达到线速多播的要求，为了能够方便描述和证明多播单元以及由其构成的多播网络特性，本文将从分配格的理论角度来说明。

2.2 布尔多播交换单元

在表1中定义输入控制的基础上，可以进一步定义Ωroute={0-bound,1-bound,i dle}，即0−bound=10; 1−bound=11,idle=00。故 10＜00＜11 的线性排序等于如下规则的顺序。

规则 1 0−bound＜idle＜1−bound

路由单元按照规则的序列排序即可将尽可能多的有效分组转发到预定的输出端口。当出现2个0-bound分组或2个1-bound分组的输出争用时，BAR/CROSS状态的选择依赖于特定的应用，如信号的优先级。这样的操作不影响信号自路由的最优性。

当排序单元应用于多播时，必须定义新的带内信令和相应的交换控制方式，例如表2所示。

表2 支持多播以线速扇出的2×2多播排序单元的信号控制

表2中，B表示BICAST多播分组（如图2(d)、图2(e)所示）；I表示IDLE空分组。

可见支持多播的自路由带内信令控制表必须扩展为Ωbicast=Ωroute∪{bicast}。

这个扩展集合由规则1和规则2各自部分排序得到。多播单元对属于集合Ωbicast的信号执行排序，当idle遇到bicast时交换控制遵循规则3。

规则 2 0−bound＜bicast＜1−bound

规则3 output-0端口输出信号值0-bound，output-1端口输出信号值1-bound，其后都跟随着相同的负载。

这样，分组的负载在通过多播单元时可以是BAR状态、CROSS状态或者BICAST状态的硬件电路拷贝的线速多播方式。按这种方式，多播单元能将尽可能多的分组负载转发到其预定目标端口。

为了能够方便分析多播单元的特性，排序规则1、2与交换规则3需要寻求一种可以同时满足3种排序规则的理论，而分配格理论刚好能够满足需求。格是一个有二元操作数布尔和∨与布尔积∧，且遵守布尔交换律、布尔结合律、布尔幂等律、布尔吸收率的集合[15]。

常见的格是遵守布尔操作中并集和交集运算的集合的一组子集。

规则4 a≤b⇔a∧b=a

根据规则4，每一个格都可以导出一个部分有序序列。如果一个部分有序集合（简称偏序集）中任意两元素存在一个最大下界和一个最小上界，则称这个偏序集为偏序格，用布尔和与布尔积表示这2个界限，偏序格逻辑上等同于格。图3所示为2种格的举例，其中图3(a)是有3个变量的自由格，图3(b)为分配格。

根据规则1和规则2，图3(b)描述了Ωbicast的部分排序，很明显偏序集Ωbicast具有偏序格的特性，因此被称为格。至此多播单元运行的3个规则1到规则3能够被统一于以下布尔规则（规则5）。

规则5 输出端口0的值为2个输入的布尔积，输出端口1的值为2个输入的布尔和。

如果一个格满足分配律

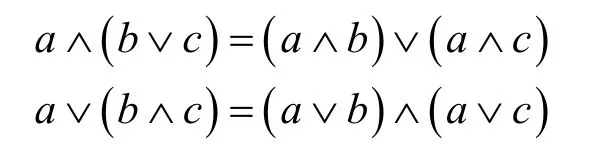
则此格为分配格。Ωbicast就是一个简单的例子，如图 3(b)所示。因此有时也把该多播单元称为布尔单元。

图3 2种格的举例

本研究采用分配格来构建多播排序和多播交换的自路由带内信号表。到目前为止，常用交换结构信号表使用的都是线性有序集，尤其当信号值为数字表示的时候更是如此。对所有带内信号进行完全排序的要求不仅限制了结构的应用范围，而且完全阻碍了多播操作。把2×2多播单元与2×2单播单元从分配格的角度来对比可以清楚地看出这一点。

2.3 多播集线器到布尔多播集线器一般化

定理1 （多播集线器定理[16]）以排序单元多级互联网络构建的n-to-m的集线器（n个输入，m个输出的集线器）为参考，将其中的排序单元用多播单元替换。记信号表为Ωbicast，不妨设，输入 V0个 0-bound，V1个 1-bound，以及VB个多播信号。可得到以下结论。

结论1 上面n−m个输出端口最大可能产生共min｛n-m,V0+VB｝个0-bound和多播信号。

结论2 下面 m个输出端口最大可能产生共min｛m,V1+VB｝个1-bound和多播信号。

2.2 节把基本交换排序单元统一到布尔单元并用布尔代数来描述，此处由基本单元多级互联构成的多播集线器同样用布尔代数来描述。

定义1 令Vj(0≤j≤n)为n个变量 X0,X1,…,X(n-1)的合取范式。若1≤m＜n，当

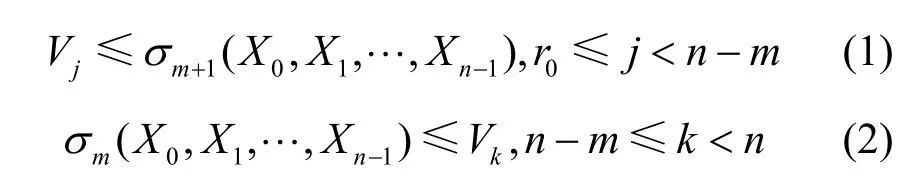
成立时，相应的布尔交换器被称为是n-to-m布尔集线器。

n×n布尔排序器在一定条件下等同于布尔集线器。如2×2布尔排序器和2-to-1布尔集线器，其实和布尔单元一样。

推论1 当Vj和σk应用在任意分配格中的n元素而不是变量 X0,X1,…,X(n-1)的时候，式(1)、式(2)在定义1中仍是正确的。

在推论1中分配格的假设是关键，因为分配率的应用在合取范式中的作用是非常重要。当一个有序集合是分配格时，布尔集线器相对于普通集线器是一个高级版本。

定理2 （布尔集线器的0-1原理[16]）当且仅当输入任意包含n−m个0和m个1的序列后，上面的n−m个端口输出值为0，下面m个端口输出值为1时，n×n布尔交换器就是n-to-m布尔集线器。

3 大规模扩展线速多播交换结构模型

为了构建大规模扩展多播交换结构模型，本文把“统计线组”[15]技术应用到2.1节的分治网络中。将自路由分治网络中的每一个2×2节点放大为2G×2G节点，并用 2G-to-G布尔多播集线器替换该节点，交换网络中每一根连接线用一束共G根线替换，从而构造了一个带有统计复用特点的多播自路由结构，每G根输出线共享一个群组地址。由于通信波动和突发性引发的分组丢失率随 G值的增大呈指数级减小[13]，在可允许的输入流量下，“统计线组”技术可以达到几乎无阻塞交换。

在实际应用中G表示为群组，将G根线组成的一束记为一个群组，这个值一般比较大，K表示群组数，N表示交换结构的输入/输出的总线数N=KG。

如图 4(a)所示为一个 N=128，K=16，G=8的多播路由交换结构。该结构是通过将 16×16的banyan网络中每一个2×2节点替换为2G-to-G的由布尔单元组成的布尔集线器来实现。这里G=8，在实际应用中G本应该为一个大的数，所以一个2n×2n banyan-type的G-line版本的网络构建成了一个 N×N的几乎无阻塞的多播交换器。根据 fast knockout[17]集线器构造算法或利用 bitonic circular再配合一级半清器（half-cleaner）[15]，可构造G为任意大小的群组集线器，从而保证了交换结构的大规模可扩展性能。

图4 布尔多播集线器交换结构及内部结构

图4(b)所示为图4(a)中任一个2G-to-G的布尔多播集线器的内部结构图。图4(b)中的每一级（除了最后一级地址过滤器）中最小的单元即为2.2节的布尔多播交换单元。由图4可以对本文提出线速多播交换的内部结构有一个更详细的理解。

本文提出的线速多播交换模型所采用的完全自路由分治网络结构和布尔多播集线器都具有良好的大规模可扩展性，交换结构中每个最小的交换单元使用硬件电路拷贝的方式实现多播，从而保证了交换结构的线速多播以及大规模可扩展特性。此外，交换结构模型中无排队缓存，更不需要调度从而保证了多播时延不会高于某一个定值。

对于定理1，当有一个适当的多播信号表Ωbicast为输入时，多播集线器就能够达到最优的多播交换。而多播交换网络则是由多播集线器递归构造而成，当用布尔单元代替集线器网络中的排序单元时，对任意的一个格或分配格结构的信号表，该定理是否也成立。由此深入考虑Ωbicast格结构的支持多播集线器定理的本质属性，仔细观察发现Ωbicast在结论1中分为上部理想{0,B}和下部理想{1,1}，在结论2中类似地分为{1,B}和{0,1}。

定理3 如果格 Ω的非空子集 S满足条件x∈S,y∈S⇒x∧y∈S,x∨y∈S，则S为子格；如果x∈S,y∈S⇒x∧y∈S，则子格S是一个上部理想；如果x∈S,y∈S⇒x∨y∈S，则子格S是一个下部理想。

定义2 如果2个格之间映射保持布尔运算不变，则称该映射为格同态。

如从格Ω到Ω2的格同态等同于格Ω划分为一个上部理想和一个下部理想。

定理4 设μ是格Ω映射到Ω2的一个同态，那么格Ω上部理想为μ-1(0)和下部理想为μ-1(1)。若将格 Ω划分为上部理想 U和下部理想 L，对s∈U ,μ(s)=0和s∈L,μ(s)=1，则可以得到μ是格Ω到Ω2的同态。

定理5 对于由排序单元多级互联网络构成的n-to-m集线器，用布尔单元替换多级互联网络中所有的排序单元，所得到一个n-to-m布尔集线器网络便称之为布尔集线器。

将任意的分配格Ω划分为上部理想U和下部理想L。从U中输入u个值，0≤u≤m，从L中n-u个值进入集线器网络之后，有如下结论。

结论3 上部n−m个端口输出min{n-m,u}属于U的值。

结论4 下部m个端口输出min{m,n-u}属于L的值。

证明 根据定理5可知上述的单元为一个n-to-m布尔集线器。为了证明定理剩下的部分，令μ表示和s∈L,μ(s)=1中Ω到Ω2的同态。

用μ(s)替换每一个输入信号 s。这就将 n个输入信号值转变为u个0的和n−u个1的组合。从集线器网络的性质可知，上部n−m端口输出为min{n-m,u}个0和下部n端口输出个1。因为μ是一个格同态，级间用同样的信号替代。当替代后集线器的一个输出端口输出值0或1时，则替代前其输出值分别属于μ-1(0)=U 或μ-1(1)=L。证毕。

将定理5应用到Ω=Ωbicast，U={0,B}，L={I,1}，那么结论1和结论3变为完全相同。类似地，U={0,1}和L={B,1}结论2将和结论4一致。

定理6 针对大规模可扩展多播结构中的n-to-m集线器，将所有的排序单元用bicast单元来替换，则当信号表是Ωbicast时，以下结论中有一项成立。

结论5 上面的n−m个端口输出仅为0-bound信号。

结论6 下面的 m个端口输出仅为1-bound信号。

结论7 没有端口输出为idle信号。结论8 没有端口输出为bicast信号。

证明 信号值 0-bound，1-bound，bicast和idle分别为0，1，B和I。bicast单元组成的多级互联网络的精确输入组合为：V0个 0，V1个 1，VB个B，VI个I。由图3(b)可看到该信号表满足分配格的结构，若将多级互联网络中的 bicast单元用布尔单元替换，则布尔集线器定理得以应用，同时也保证了布尔集线器网络构成及式(1)、式(2)的应用。证毕。

将信号表Ωbicast表示的格划分为上部理想U={0,B}和下部理想L={I,1}。可以得到由n元组构成的对称多项式σm+1的如下性质。

性质1 如果 V1+VI≥m+ 1，可得 σm+1的值不是1就是I，因为σm+1中的一些单项式只与n个变量中赋值为1和B的值的变量有关。

性质2 如果 V1+VI≤m+ 1，可得 σm+1的值不是0就是B，因为σm+1中的一些单项式只与n个变量中赋值为0或B的值的变量有关。

另一种是，将理想的分为上部分U={1,B}和下部分L={0,I}。同理可得以下性质结论。

性质3 如果 V1+VB≥m+ 1，可得 σm+1的值是1或B。

性质4 如果 V1+VB≤m + 1，可得 σm+1的值是0 或 I。

假设性质2和性质4成立，σm+1唯一可能的值就是0，再由式(1)可以得出结论4成立。

对称地，假设性质1和性质3成立，σm+1唯一可能的值就是1，因此σm=1，再由式(2)可以得出结论6成立。

假设性质2和性质3成立，σm+1唯一可能的值就是B，因此σm≥σm+1=B。从式(1)可以得出，上部分n−m 个端口输出不可能为I。从式(2)可以得出，下部分m个端口输出也不可能为I。所以结论7可以成立。

由对称的特性可得，在性质1、性质4假设下结论8也成立。

在定理6中，0-bound和bicast信号总数在多级互联网络被逐级保留，1-bound和 bicast信号总数亦然。同样可以看出结论5到结论8的每一个声明都暗示着结论1和结论2成立。因此定理6应该可以说是布尔多播集线器原理的一个详细版本。从定理6可以得出一个更通用的结论：布尔集线器理论不仅仅可以把尽可能多的信号路由到目的输出群组，而且可以依据“优先级”的不同而达到最佳路由。此处的“优先级”要求集线器的信号表必须是分配格。这个定理适合通过各种可能的方式去划分分配格的上部理想和下部理想。通过以下例子来说明。

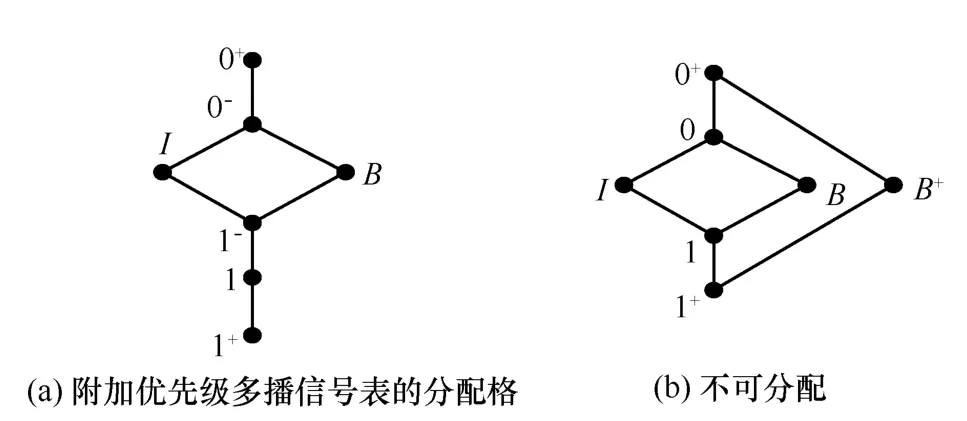
图5 优先级多播信号表示例

设Ω={0+,0-,I,B,1-,1,1+}为在图 5(a)中的分配格。Ω中元素的命名规则为：上标‘+’为到达期望集线器的目的地址0或1的最高优先级，‘−’表示最低优先级。Ω中所有通过一个n-to-m布尔集线器的路由信号的优先级涉及了所有可能的对 Ω的划分为上部理想U集合和下部的理想L集合。这里可以组合

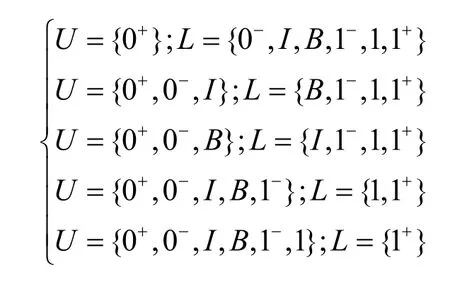
从定理5可以看出，在去往输出群组0的元素中集合U中的每一个元素都比集合L中的元素的优先级要高；同样，信号路由到输出群组1也是如此。应用这个理论到上面所列出的5个划分方法可以得到以下结论。

结论9 在有序子集{0+,0-,B,1-,1,1+}的信号中去往输出群组 0的较小的元素被赋予较高优先级，然而去往输出群组1的信号被赋予较高的优先级。布尔集线器的路由最佳性是和这个优先级的策略相一致的。

结论10 类似的优先级处理同样可以应用在有序子集{0+,0-,I ,1-,1,1+}中。

结论11 同时，B和I这2个信号在路由向任意输出群组时被赋予同样的优先级，这就意味着B和I不能同时出现在彼此对立的输出群组中。

如图6(a)实例说明分配格Ω的信号通过一个8-to-4布尔集线器网络的传播过程，其中有上标‘+’的信号是具有高优先权处理的。0，1，B，I分别表示 0-bound，1-bound，bicast和 idle。图中阴影部分单元表示发生多播的信号，在这里bicast和idle信号被0-bound和1-bound信号所替换。这样输出群组0得到尽可能多的0-bound和bicast信号，同时输出群组 1得到尽可能的1-bound和bicast信号。此外，这个路由最优是和结论9和结论11相一致的。

例如，图6(b)例证了图5(b)中非分配格Ω={0+,0-,I,B,1-,1,1+}中信号值通过同一个8-to-3布尔集线网络的传播过程，其理想的交换是得不到保障的。因为在这个格中 B+∧I=0+和B+∨I=1+，一个高优先级的bicast信号在一个布尔单元中遇到一个idle信号后输出高优先级0-bound和1-bound信号，从而导致输出群组0丢失了一个有效信号，同时也只有一个有效信号出现在输出群组0。这个次优的路由结果反应了在定义布尔交换，集线器或排序器中输入信号需要满足分配格的结构才能达到最优的多播交换。

图6 信号通过布尔集线器网络传播过程

在实际应用中非分配格有时会被用作信号表，因为高优先级多播通信在整个通信量中占很小一部分，那么布尔集线器理论依旧能够被统计应用，这是一个特殊情况。

4 线速多播结构阻塞率模型分析

从上述布尔多播单元 bicast的状态可以看出，该多播交换结构的特点是在交换网络中线速扇出。当扇出为1时即是单播，否则就是多播，所以该交换多播交换结构支持单多播的混合输入。分组的扇出率（多播扇出的个数）直接影响了其阻塞率。由于交换的规模是由其级数决定的，交换规模越大，多播分组扇出的可能性也就越大，交换的级数对阻塞率和扇出率也有直接的影响。

单播时自路由路径 trace(guide)[15]信息表示为dφ(g)… dφ(2)dφ(1)1，其中，下角标φ (1),φ(2),…,φ(g)表示级间置换信息[13]。多播分组头信息序列为…Q110Q010Q100Q000Q01Q10Q00Q1Q01，多播分组头信息的第一位1为多播有效位，此分组序列包含了该多播中所有单播的信息，从右向左依次排序，可以分解为多个单播分组的信息头，并且都满足单播的级间置换规则。

不妨设第 i(1≤i≤m)级布尔集线器内单播分组控制信令为dφ(i)，多播分组控制信令为Qqi1，qi是二进制数，其长度为i−1。每当空分组I与多播分组B在同一个2×2的布尔单元相遇时，若该级满足多播扇出控制要求，其两端口的输出控制信息则采用cut-through[15]的方法将多播信息头进行分割，否则多播头信息不发生变化。

下面具体分析线速多播交换结构在不同网络负载下的分组阻塞率情况。假定各输入群组所到达的分组满足独立同分布的要求，在某一时隙到达交换结构网络中第i级2G-to-G布尔集线器中某交换单元某输入/输出群组的分组数目表示为XIi/XOi(1≤i≤m )，其中，0≤XIi≤G,0≤XOi≤G 。

设交换结构到达的业务数据总额为1，单播业务所占比例参数λ=P1，表示在单个时隙内单播业务到达的概率为P1，多播业务所占比例参数为λ=P2，表示单个时隙里多播业务到达的概率 P2，用XI1s表示进入交换结构的第一级中某输入群组的单播分组个数，则

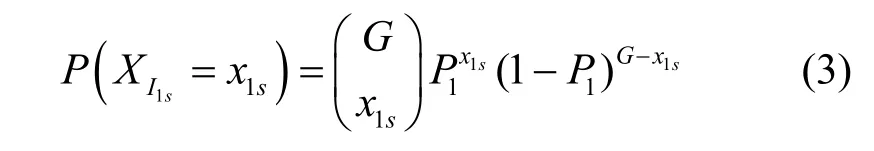
其中，XI1m表示进入交换结构的第一级某输入群组的多播分组个数。

P=P1+P2,x1=xs+xm，其中，xs表示单播分组个数，xm表示多播分组个数。如果xm≠0，表示存在多播分组，由于多播分组扇出的特点，那么在交换结构中的某集线器最后输出的分组个数在一定概率上要比输入的分组多一些。假设每个多播分组在交换结构的每一级都要求发生多播，即其带内多播控制信号全是由2k-1个B构成，由于布尔集线器的输入信号表为严格的分配格结构，即当单播与多播在集线器内争用同一个出口时，根据交换规则单播优先级高而占用输出端口，导致其多播会被误路由，所以该多播只能以一定的概率扇出。XI1，YI1为交换结构中第一级集线器的输入，满足独立同分布要求。用AI1表示第一级布尔集线器输入分组的总和。为了简化表达式用DI(di)表示 DI=di时的概率P(DI=di)。

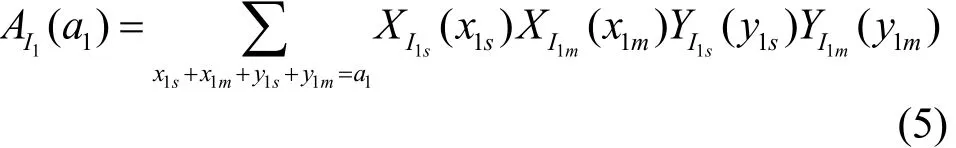
∀a1≤2G,∃I∧B=0,I∨B=1，使a1+x1m2+y1m2≤2G，其中，x1m=x1m1+x1m2，y1m=y1m1+y1m2，x1m1，y1m1为扇出为1的多播分组（即为单播分组），x1m2，y1m2为扇出2的多播分组。从而可得实际的输出分组总和

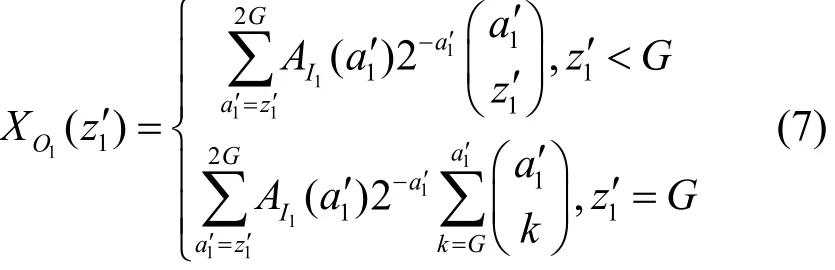
其中，λ1m=1-λ1s，λ1m=1-，已知多播交换结构的第i级集线器的输出是第i+1级集线器的输入，即满足相同分布，由此可得集线器实际输入的分组总数ai+1服从以下分布。

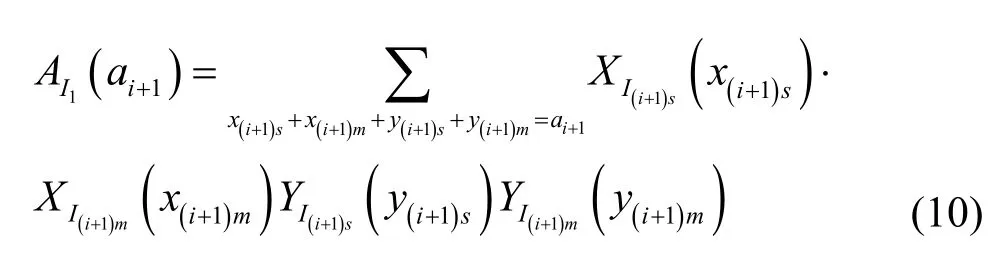
集线器实际输出的分组总数ai′+1服从以下分布。

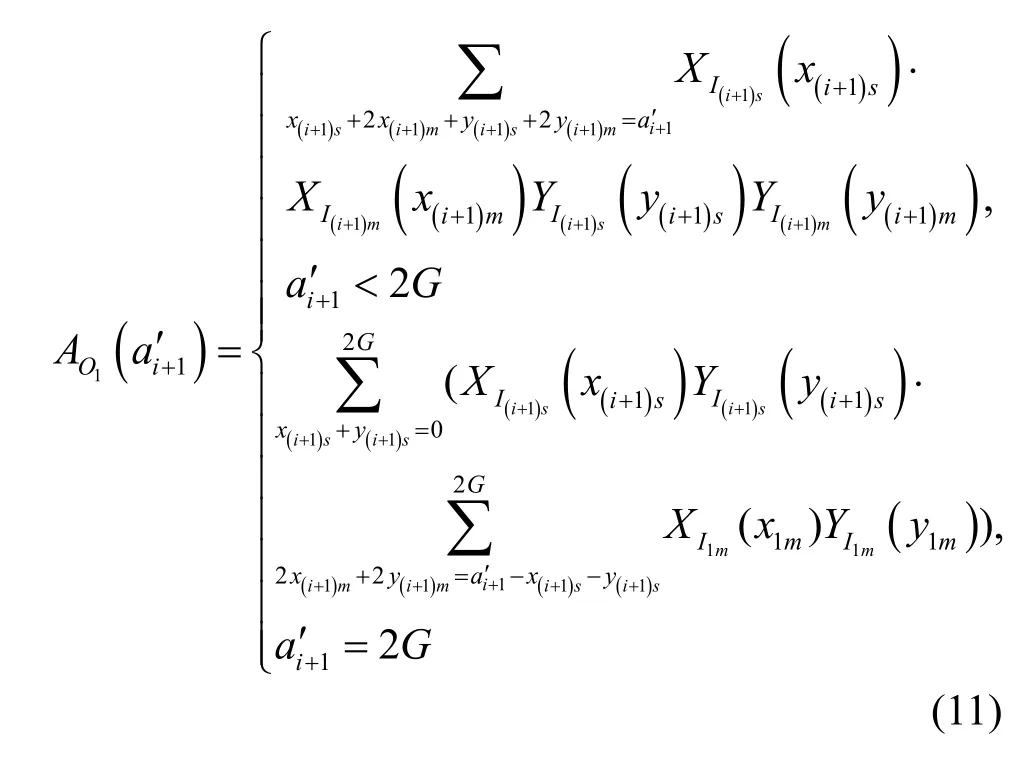
同样可得出第i+1级布尔集线器的某输出群组单多播分组总数的分布：

重复上述步骤可以推导出第i+1级布尔集线器输出的单播分组个数XO(i+1)s分布，以及多播分组个数XO(i+1)m分布。通过的迭代的方法，可得第k级布尔集线器某输出群组单多播分组个数的分布情况 XOks，XOkm。

单播阻塞率指平均输入单播分组减去输出单播分组数的平均值后再与平均输入单播分组数的比，得式(13)。

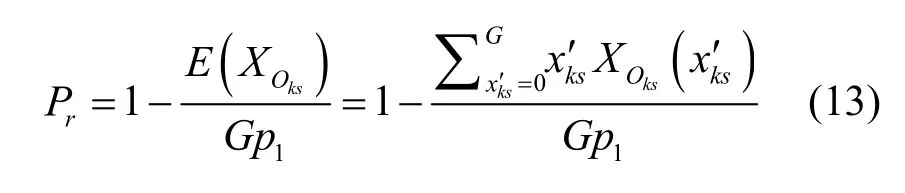
多播的阻塞率要考虑扇出的因素，多播的输出分组会远大于输入分组，所以多播的阻塞率应该为平均输出多播分组数与理想最大输出多播分组数的比，得式(14)。其中，(k+1)Gp2mod(G-Gp1)的含义为：因带内控制信令由全B组成，所以理想最大可扇出分组数可表示为(k+1)Gp2，但受到输出端口数G的限制和单播输入分组数Gp1的与多播分组争用端口的影响，最大可输出多播分组数表示为(k+1)Gp2mod(G-Gp1)。

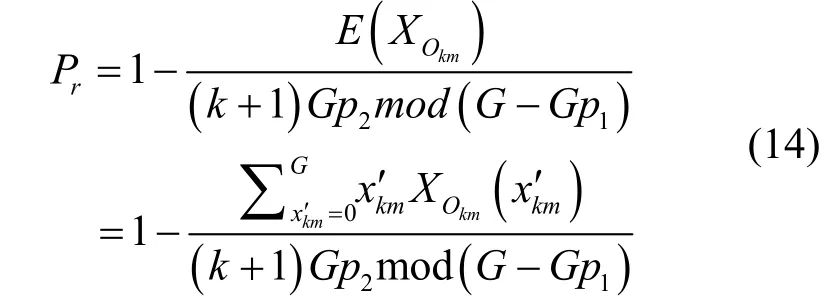
5 仿真结果

本节采用C++编程实现在均匀分布业务源下对线速多播交换结构的多播阻塞率和时延的仿真。阻塞率是指分组在经过交换系统时没能被成功交换到目的端口的概率。时延是指分组第一个比特进入交换系统到分组第一个比特从交换系统输出时所需要的时间。时延在交换系统中一般分为传播时延和信号处理时延。仿真过程要求数据源满足伯努利均匀分布，集线器的群组输入业务要求服从二项分布，到达的业务强度用归一化负载表示。

1)多播阻塞率仿真

负载强度对阻塞率有直接的影响，本节选取一个一个代表性的负载，不妨设单播业务所占负载的比例为P1=0.2，则可得多播业务所占负载的比例为0≤P2≤1-P1。在多播业务强度相对固定的情况下，通过改变交换网络的级数参数K以及群组参数G的大小仿真多播阻塞率的情况。选取在K=4的条件下仿真并比较 G=8,16,32时多播的阻塞率情况。从图7可以看出，随着G增大其阻塞率而减小。因为参数K决定了交换结构网络的级数，当K不变且单播业务负载强度相同时，则单播与多播在集线器中发生争用的情况基本相同。然而若G变大，分组在布尔集线器内部发生争用的概率就变小，阻塞率也就越小。

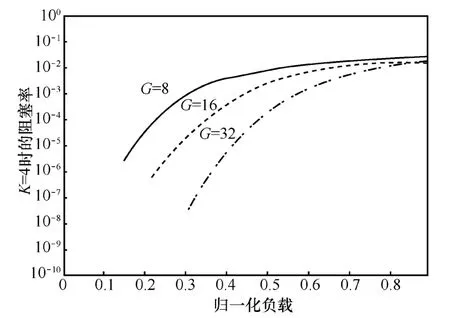
图7 G不同时的多播阻塞率

图8的显示的是群组G=32时，K=4、8、16时得到的多播阻塞率仿真结果。从图中曲线可看出K变大其阻塞率也变大，然而在同一负载点上，K的不同，其阻塞率区别不明显。这是因为由于多播的扇出特性，当交换结构网络级数不小于 4，归一化负载P2≥0.2时，得到扇出的多播分组数接近G-0.2G=0.8G所以在最后的几级布尔多播集线器中多播分组被扇出的概率会很小，所以在G=32归一化负载下，虽然k不同，但其阻塞率差别并不明显。

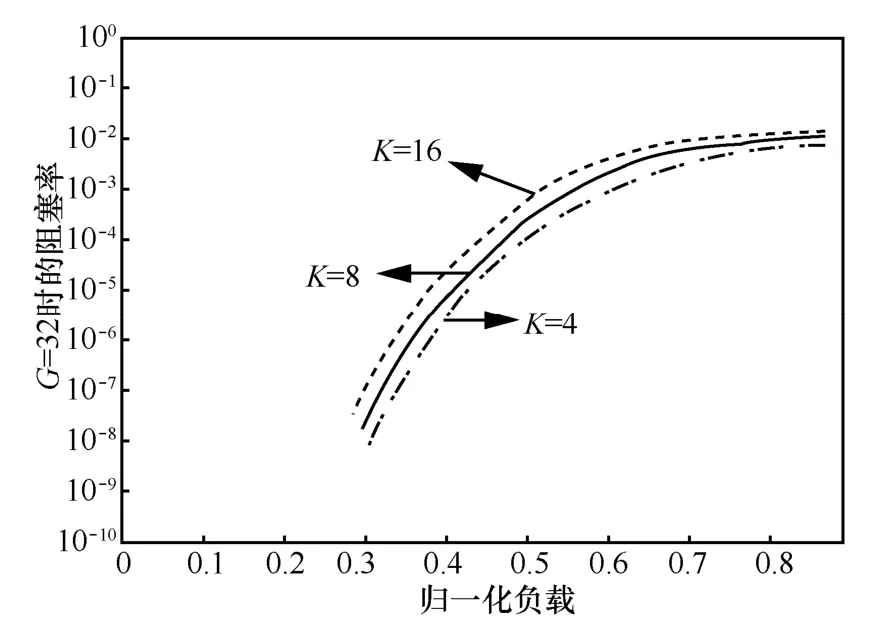
图8 K不同时的多播阻塞率

2)多播分组时延仿真

多播分组在经过交换结构网络的每一个布尔集线器中的每一个2×2布尔单元时，需要一定的时间完成对分组数据的处理，从而产生了时延。所以多播分组的时延主要由分组所经过基本布尔单元个数决定，设分组在经过任一个布尔单元时对数据处理的时间即时延为Δd。

多播交换结构网络的规模由k决定，每一个布尔集线器的规模则是G决定，交换结构中布尔单元的个数则是由K和G共同决定。为了仿真多播时延数据，不妨先固定一个参数，设K=4，可以得到G=8,16,32的时延，如图9所示。

从图9中可看出G越小时延也越小。从图中还可以看出 G不同时，各时延增长速度Tv的关系为Tv(G=32)＜Tv(G=16)＜Tv(G=8)，这是因为G=32的阻塞率是最小的，所以分组丢失的概率较小，统计分组时延也就会最低。随着负载的增大，当负载大于 0.6时，时延增加的速度加快。

固定参数G=32时，得到K=4、8、12的时延仿真结果，如图10所示，K越小其时延越小，K不同。从图8可以得知，K不同，其阻塞率的变化不明显，所以该时延曲线的变化也不明显。该多播交换结构采用的多级互联的结构，无论G，K参数如何变化，其时延也总会小于某一个定值。

图9 K=4，G不同时的多播时延

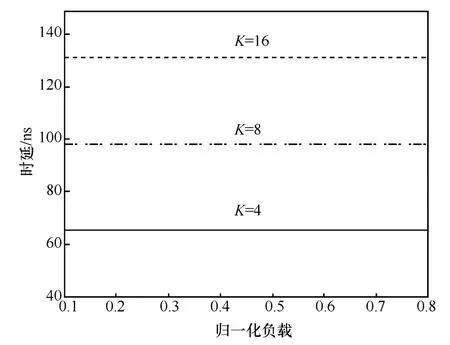
图10 G=32，K不同时的多播时延

6 结束语

本文提出的基于分配格的线速多播交换模型，具有低时延、无抖动、可大规模扩展优点，当多播业务负载强度控制在一定可允许的范围内时，其多播业务的阻塞率可以被接受，其多播时延总会小于某个定值，且该定值会在百纳秒量级，所以该交换结构能够为到达业务提供时延上限保障。该交换结构模型可以解决某些网络环境中对业务的特殊需求应用的问题，如时延、阻塞率、线速多播等。

[1]HUANG A. Starlite: a wideband digital switch[A]. Proc Globecom'84[C]. Atlanta,GA,1984.1-5.

[2]SAITO H,YAMANAKA H,YAMADA H,et al. Multicast function and its LSI implementation in a shared multibuffer ATM switch[A].Networking for Global Communications,13th Proceedings IEEE[C].Toronto,Ont,1994.315-322.

[3]YEH Y S,HLUCHYJ M,ACAMPORA A. The knockout switch: a simple,modular architecture for high-performance packet switching[J].Selected Areas in Communications,1987,5(8):1274-1283.

[4]CHAO H J,CHOE B S,PARK J S,et al. Design and implementation of abacus switch: a scalable multicast ATM switch[J]. Selected Areas in Communications,1997,15(5):830-843.

[5]LEE T T. Nonblocking copy networks for multicast packet switching[J]. Selected Areas in Communications,1988,6(9): 1455-1467.

[6]CHAO H J,LIU B. High performance switches and routers[M].Wiley-IEEE Press,2007.

[7]MARCHOK D J,ROHRS C E,SCHAFER R M. Multicasting in a growable packet (ATM)switch[A]. INFOCOM'91. Proceedings. Tenth Annual Joint Conference of the IEEE Computer and Communications Societies Networking [C]. BalHarbour,FL,1991. 850-858.

[8]JASTRZEBSKI A,KUBALE M. Rearrangeability in multicast clos networks is np-complete[A]. Information Technology(ICJT)[C]. Gdansk,2010,183-186.

[9]HUI J Y,RENNER T.Queueing analysis for multicast packet switching[J]. IEEE Transaction Communications,1994,42(234): 723-731.

[10]ALI MK M,YANG S. Performance analysis of a random packet selection policy for multicast switching[J]. IEEE Transactions Communications,1996,44(3):388-398.

[11]MARSAN M A,BIANCO A,GIACCONE P,et al. Multicast traffic in input-queued switches: optimal scheduling and maximum throughput[J]. IEEE/ACM Transactions on Networking (TON),2003,11(3):465-477.

[12]PAN D,YANG Y. FIFO-based multicast scheduling algorithm for virtual output queued packet switches[J]. Computers,IEEE Transactions,2005,54(10):1283-1297.

[13]HE W,LI H,WANG B,et al. Load-balanced multipath self-routing switching structure by concentrators[A]. IEEE International Conference on Communications,ICC’08[C]. Beijing,China,2008.5935-5939.

[14]LI H,LI S Y R. Layout complexity of bit-permuting exchange in multi-stage interconnection networks[M]. Boston: Kluwer Academic Publishers,2001.259-276.

[15]LI S Y R. Algebraic switching theory and broadband applications[M].Academic Press,2001.

[16]LI S Y R. Unified algebraic theory of sorting,routing,multicasting,and concentration networks[J]. IEEE Transactions Communications,2010,58(1):247-256.

[17]LI S Y R,LI H,KOO G M. Fast knockout algorithm for self-route concentration[J]. Computer Communications,1999,22(17):1574-1584.

[18]LI H,LI S Y R. On the Complexity of Concentrators and Multi-stage Interconnection Networks in Switching System[D]. Hong Kong: Chinese University of Hong Kong,2011.