大尺度溶洞型油藏试井模型建立与求解
杨芳* 吴小庆 李进
(1.乐山职业技术学院;2.西南石油大学理学院;3.中国石油西南油气田分公司勘探开发研究院)
杨芳等. 大尺度溶洞型油藏试井模型建立与求解. 石油规划设计,2014,25(4):27~30,41
缝洞型油藏储渗空间以大洞穴和大裂缝为主,基本特点是孔隙大,流动性强,流动区域的边界复杂,流动网络呈非线性分布。溶洞与井通过裂缝相连通,溶洞大小对试井曲线形态的影响较强。溶洞越小,生产期压力下降越大,相同时间恢复达到的地层压力越小[1]。常规试井理论是建立在连续介质渗流理论的基础上,并不适用于大尺度缝洞型油藏的试井解释。实践表明,通过常规试井解释的结果所反映的地质特征往往与实际油藏相差甚远,从而导致油田试井作业处于停滞状态[2]。将常规试井解释结果作为初值输入,通过非线性多参数拟合进行试井解释,能够获得符合实际情况的解释结果[3]。因此,在研究油气藏的渗流规律时,仅根据储渗空间类型和特征尺度建立多重介质渗流模型并不完善,还应考虑不同介质间窜流的方向性。只有当油气藏不同介质间的窜流为标量时才能采用多重介质渗流模型描述其渗流特征[4]。
针对当前试井解释现状,本文在常规试井模型的基础上,建立了适用于大尺度溶洞型油藏的试井模型。在有界地层中以大溶洞作为“源”项,考虑井筒与溶洞相连的实际地质状态、连续性及质量守恒,建立基于偏微分方程的数学模型。采用正交变换法[5]导出模型的解析解,并通过数值试验,分析井底压力动态特征及影响因素。
1 试井模型的建立
对实际情况进行分析,大溶洞并不是孤立的溶洞,它是由若干小溶洞汇集而成的。小溶洞在大溶洞里是均匀分布的,井筒并不是直接与地层连通,而是通过地层中的裂隙连通,流源强度视为一致的均匀连续分布,垂直井段为全打开的。建立如图 1的坐标,得到如图1所示的物理模型。
基本假设:一是,在各向异性的非均质油藏中,油藏为一有界区域,地层宽度为lx,地层长度为ly,地层厚度为lz;二是,溶洞作为体“源”,单位时间内流入井的总流量为Q(t);三是,忽略重力影响,恒定黏度及压缩系数的微可压缩液体单相流动。

图1 大尺度溶洞与井筒连通物理模型
在井筒切面处(即y=0平面)有流量进入,井筒截面长为l4-l3,宽为l2-l1,在井筒截面所在平面的边界条件为:

在其他面上是绝流的,即均为第二类齐次边界条件。
在以上假设条件下,根据连续性方程、状态方程、质量守恒方程[6],以及地层的实际情况建立如下溶洞通过地层与井筒相连接的试井模型。

f( x,y,z,t)为“源”项(即大尺度溶洞流入井筒的流量)构成的自由项,表达式为:


将式(2)代入式(1),对其进行无因次变换,经过一系列推导得到:

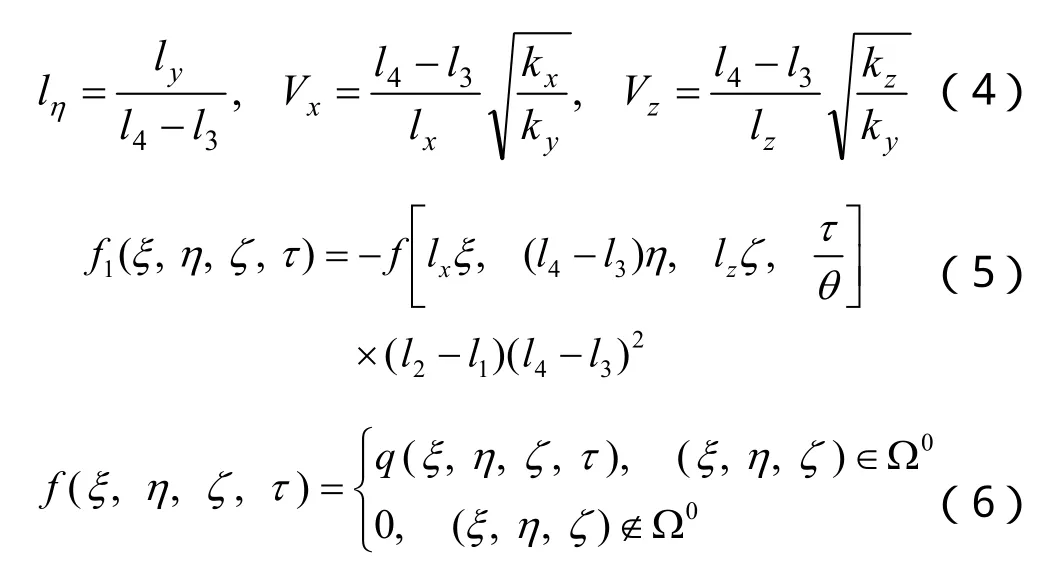
2 模型的解析解
利用正交变换法将偏微分方程的初边值问题(3)转化成常微分方程的初值问题,注意方程及边界条件的特点,考虑如下特征值问题[7]:

利用特征函数系的完备正交性,引入Ω上的有限正交变换[5][7],对式(3)进行正交变换,经过一系列推导得如下常微分方程的初值问题:

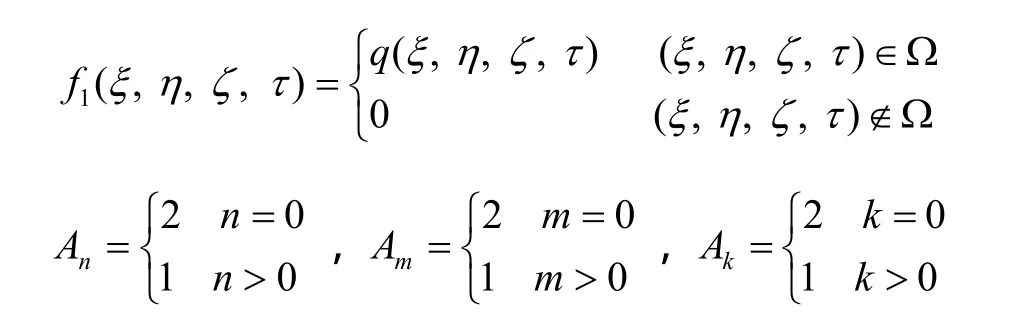
由齐次化原理求解此常微分方程可得:

再利用逆变换易得偏微分方程的初边值问题(3)的解见式(10)。
将式(10)代入式(2)得关于地层内的流体压力的解析解式(11)。
由上述解析解的精确表达式可知积分函数是依赖于流量函数q的,还可知大尺度溶洞的压力分布是各个小溶洞体源的叠加。

3 模型压力试算


图2 溶洞无限大油藏压力及压力导数双对数曲线
3.1 裂缝储容比的影响
裂缝储容比ωf是指裂缝中通过弹性形变能产出的流体占基质、裂缝和溶洞中所有通过弹性形变能产出流体的比例。图3是在其他参数不变的情况下,改变裂缝储容比ωf对压力和压力导数复合曲线的影响。裂缝储容比主要决定着压力导数曲线第一个过渡段下凹的深度和宽度:ωf越小,过渡段就越长,凹陷就越宽且越深。
3.2 溶洞储容比的影响
溶洞储容比ωv是指溶洞中通过弹性形变能产出的流体占基质、裂缝和溶洞中所有通过弹性形变能产出流体的比例。图4是在其他参数不变的情况下,改变溶洞储容比ωv对压力和压力导数复合曲线的影响。溶洞储容比ωv决定过渡段曲线下凹的深度和宽度,但与ωf不同,随着ωv的增大,过渡段凹陷就越宽且越深。对比图4和图3还可以发现,溶洞储容比ωv对压力导数曲线产生影响的时间要晚于裂缝储容比ωf。

图3 裂缝储容比对复合曲线的影响

图4 溶洞储容比对复合曲线的影响
3.3 溶洞与裂缝之间窜流系数的影响
窜流系数λv对复合曲线的影响见图5。
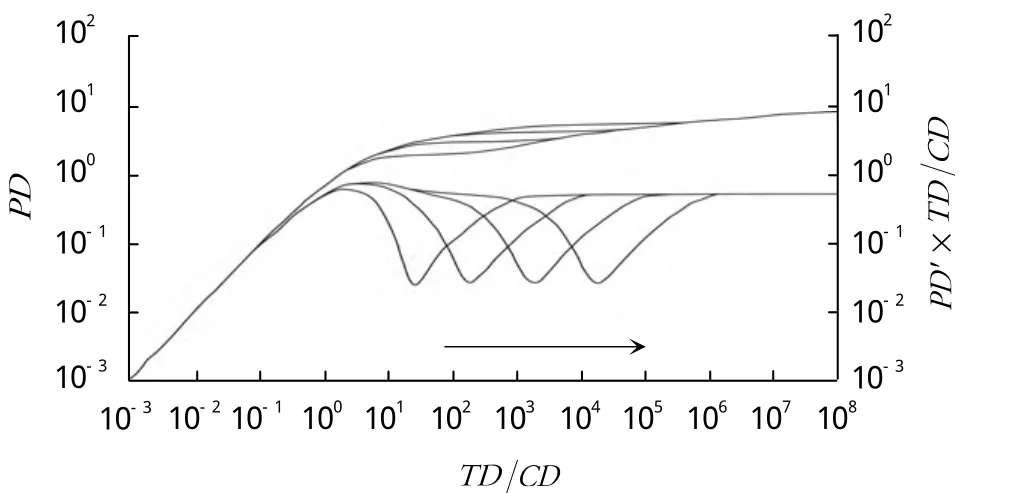
图5 窜流系数对复合曲线的影响
窜流系数λv影响过渡段出现的时间,窜流系数的值越小,则过渡段出现的时间越晚,压力导数曲线上的凹陷就越往右移。
4 结论
本文引入了解决石油勘探开发问题中常用模型的“正交变换法”,这对丰富数学物理方程在石油工程计算中的应用具有非常重要的理论意义。该方法能求得模型在实空间的解析解,在解决石油工程问题中起到了化繁为简的作用。建立了溶洞型油藏试井偏微分方程模型,直接从解析解出发编程,形成了相应软件并进行计算,根据计算结果分析了试井理论曲线的基本特征和影响因素。
符号说明:
[1]王新海,张冬丽,李江龙.含有大尺度裂缝、溶洞的缝洞型油藏的数值试井模型[J].江汉石油学院学报,2009,31(6): 129-135.
[2]彭小龙,杜志敏,刘学利,等.大尺度溶洞裂缝型油藏试井新模型[J].西南石油大学学报,2008,30(2):74-77.
[3]姚钧,戴卫华,王子胜.变井筒储存的三重介质油藏试井解释方法研究[J].石油大学学报(自然科学版),2004,28(1): 46-51.
[4]彭小龙,杜志敏,威志林,等.多重介质渗流模型的适用性分析[J].石油天然气学报,2006,28(4):99-101.
[5]吴小庆.求解裂缝性储层渗流问题的正交变换法[J].西南石油学院学报,1992,14(11): 76-86.
[6]姜礼尚,陈钟祥.试井分析理论基础[M].北京: 石油工业出版社,1985.
[7]吴小庆.数学物理方程[M].成都: 电子科技大学出版社,2004.

