二维直方图斜分最大散度差阈值分割算法

杨恢先，李 淼，谭正华，翟云龙，张建波

(1.湘潭大学材料与光电物理学院，湖南湘潭411105;2.湘潭大学信息工程学院，湖南湘潭411105)

1 引言

在图像处理和计算机视觉中，图像分割是一项基本且关键的技术，而诸多图像分割方法中，阈值法是一种简单有效的方法［1］，其关键是如何选取阈值，经过多年研究，国内外学者提出了大量阈值选取方法，如最大熵法［2］、最大相关性法［3］、最小误差法［4］、最大类间方差法［4］(又称 Otsu 法)，其中 Otsu法以目标和背景之间的类间方差作为分离性准则，对多类图像分割效果好且计算简单，成为实际中常用的方法。然而，当图像中目标和背景的面积相差很大或者信噪比低时，Otsu法会出现阈值“偏移”问题而不能实现有效分割［5］，有学者仅从类内散度出发提出新的阈值分割方法［6］，但又因没有兼顾类间散度分割效果依然不理想。针对Otsu法存在的问题，文献［7］通过引入模式识别中Fisher准则提出了Fisher准则阈值法，该方法同时考虑了类间方差和类内方差在数据分离性中的作用，使其分割结果受目标面积大小的影响较小，但类内方差矩阵可能的奇异性以及类内方差在分离性中的作用是固定的使得该算法不稳定。文献［8］对Fisher准则作了必要的修正，并基于新的鉴别准则设计了最大散度差分类器，文献［9］将最大散度差分类的思想运用到图像分割中，提出了最大散度差阈值法，该方法不仅考虑了类间方差和类内方差，而且可以避免Fisher准则所面临的类内方差矩阵的奇异性，同时还能调节参数来改变类内方差在分离性中的作用。然而一维最大散度差法(简称一维MSD法)同众多典型一维阈值分割法一样，没有考虑图像局部空间信息，当图像光照不均匀或受到噪声干扰时难以取得好的分割结果，刘建庄首次提出基于二维直方图的Otsu法［10］，很好解决了这一问题，同时也使基于二维直方图的分割算法成为近年研究的热点，有学者提出基于二维直方图的群集智能算法［11］，还有学者提出基于二维直方图的改进阈值分割输出函数的阈值算法［12］，这些算法或提高了图像分割的准确性，或降低了算法的运算时间。这里提出一种基于二维直方图区域斜分的最大散度差阈值法(简称二维斜分MSD法)，以期待获得更好的分割结果以及更少的运算时间。

2 二维直方图斜分的MSD阈值分割法

2.1 二维直方图的区域斜分

设图像尺寸为M×N，图像灰度级为L，相应的像素邻域均值灰度的灰度级也是L，f(x，y)为图像在(x，y)点的灰度值，g(x，y)为以 (x，y)为中心k×k邻域内的平均灰度值，其中 g(x，y)的表达式为:

以f(x，y)和g(x，y)组成的二元组(i，j)来定义二维直方图，直方图中任意一点的联合概率密度定义为p(i，j)，它表示二元组(i，j)发生的频率，则:

式中，cij是(i，j)出现的频数，0≤i，j≤L －1。图 1(a)为一幅图像的二维直方图。

二维直方图区域斜分:采用与主对角线垂直的一条线段g=－f+T(T为阈值，0＜T≤2L)将直方图分成0区和1区两个部分(如图1(c)、1(d)所示)，这两部分所在的点分别归为目标和背景两类，按图像灰度级与邻域均值灰度级之和的大小分割图像，像元的归类方式为:

其中，fT(x，y)表示分割后的图像。相比二维直方图区域直分模式在计算最佳阈值向量时没有考虑像素灰度级和邻域均值灰度级相差较大的点(如图1(b)中的A点和B点)，以及忽略了在对角线附近靠近阈值向量的一些区域的概率分布(如图1(b)中阴影部分)，二维直方图区域斜分模式采用与主对角线垂直的斜线进行阈值分割，计算阈值时考虑了所有区域，提高了二维阈值分割的准确性，并已被成功应用到二维 Otsu法［13］、二维最大熵法(简称二维MET 法)［14］、二维最小误差法［15］等阈值法中。

图1 二维直方图及区域划分

2.2 二维直方图区域斜分MSD法

在图1(c)、1(d)中斜线g=－f+T将二维直方图分成了对应于目标及背景的0类和1类，目标和背景出现的概率分别为ω0(T)和ω1(T):

其中:

目标和背景对应的均值矢量为:

二维斜分MSD准则采用广义差的形式，即类间方差减去C倍的类内方差为分离性度量，其数学定义为:

式中，C是一个大于零的参数，它的作用是调节类内方差在阈值分割中的作用，从而克服Otsu法当目标与背景面积相差很大时所具有的阈值“偏移”现象，改善分割效果。最佳阈值选为:

2.3 快速递推算法

对式(13)等号右边各项经变形整理可得

由式(13)、式(16)、式(17)可将类内方差整理为:

因此，从式(12)、式(19)、式(14)以及式(6)、式(7)可知求最佳阈值时需要计算 ω0(T)、ω1(T)、 μ0i(T)、 μ0j(T)、 μ1i(T)、 μ1j(T)、δTi(T)、δTj(T)，用穷举搜索的方法得到二维斜分MSD法最佳阈值的计算量很大，显然不能满足实时性要求，为此这里给出快速递推公式以进一步优化算法。对同一幅图像，μTi(T)、μTj(T)、δTi(T)和δTj(T)是固定的，所以只要计算 ω0(T)、ω1(T)、μ0i(T)、μ0j(T)、μ1i(T)、μ1j(T)就可以由目标函数式(14)求得最佳阈值，推导公式见以下两种情况:

1)当0＜T≤L－1时，如图1(c)所示，此时斜线g=－f+T的左下三角部分对应目标，可以从(0，0)点开始递推计算 ω0(T)、μ0i(T)、μ0j(T)，而ω1(T)、μ1i(T)、μ1j(T)可通过式(5)、式(9)求得。

2)当L－1＜T≤2L－2时，如图1(d)所示，此时斜线g=－f+T的右上三角部分对应背景，则从(L－1，L－1)点开始递推计算 ω1(T)、μ1i(T)、μ1j(T)，同理可得到对应ω0(T)、μ0i(T)、μ0j(T)。

采用以上递推算法，每一次计算J(T)都无需重新计算 ω0(T)、μ0i(T)、μ0j(T)和 ω1(T)、μ1i(T)、μ1j(T)，只要分别利用前面得出的ω0(T－1)、μ0i(T－1)、μ0j(T－1)和ω1(T－1)、μ1i(T－1)、μ1j(T－1)再加上直线段g=－f+T上各点相应的值即可，而ω1(T)、μ1i(T)、μ1j(T)和ω0(T)、μ0i(T)、μ0j(T)分别在 T=0，1，…，L－1和 T=2L－2，2L－3，…，L 范围内可由式(5)、式(9)和已递推出的变量求得，这样使得6个变量的搜索次数由(2L－2)减半，相对穷举算法，计算复杂度从O(L3)降到O(L)，运算量大为减少。

3 实验结果与分析

仿真实验结果是在 Matlab2007环境下，Intel Celeron R 1.67 GHz CPU/1.00 GB内存的机器上进行的。

3.1 参数C取不同值对图像阈值分割效果的影响

事实上，同一维MSD法一样，二维斜分MSD法应用在图像阈值分割中的一大特点在于，算法不仅同时考虑了类间方差和类内方差在分离性中的作用，而且可以通过调节参数C来改变类内方差在分离性中的作用，因此要使图像分割取得好的效果必须对参数C选择合适的值。现通过一幅典型红外图像car(图2(a))来说明参数C在取不同值时对图像阈值分割效果的影响，图2(b)～(d)给出了二维斜分Otsu法、二维斜分MET法、一维MSD法的分割结果用以进行比较，因限于篇幅二维斜分MSD法仅给出了C依次取0.90、1.01、1.05和1.20时所得的分割结果，如图2(e)～(h)所示，图2(j)为不同C值的二维直方图区域划分情况，图2(g)绘出了C从0.6到1.55之间以0.05为间隔的阈值变化趋势，各方法得到的最佳阈值如表1所示。

图2 红外图像car对于不同阈值法的分割结果比较及二维MSD法二维直方图区域划分解析

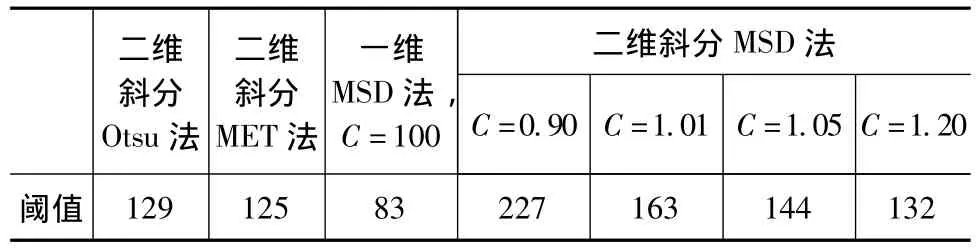
表1 不同方法取得的阈值比较

从图2(i)可以看到，这幅红外图像的二维直方图没有明显的双峰，近似为单峰，显然其代表的目标与背景的面积和方差相差很大，由二维斜分Otsu法得到的阈值偏向了较大的那个峰，不能进行有效分割(如图2(b))，同时二维斜分MET法也没能有效分割目标与背景(如图2(c))，一维MSD法在调节参数C到一个合适值后，类内方差在分类中起到调节作用，其分割结果比较理想(如图2(d))。

在图2(j)中，可以看出沿主对角线附近背景的概率分布十分集中且比例很大，而目标的概率分布零星分散且比例很小，图2(g)可以观察到当参数C逐渐增大时，二维斜分MSD法所获得的阈值逐渐减小，这使得在图2(j)中区域划分线段g=－f+T将从上向下平移，C值取较小时(如C=0.90)T*值较大，此时属于目标的很多点被错分到左下角背景区域一起，体现为分割结果目标car信息不完整且轮廓残缺(如图2(e))，C值增大到一个合适值(如C=1.01)时，g=－f+T平移到可以很好的将绝大部分目标和背景的点划分到各自对应的区域，此时将获得比较理想的分割结果(如图2(f))，而当C值继续增大(如C=1.05)时，g=－f+T继续向下平移，这时属于背景部分的点将被错分到线段右上部分的目标区域，分割结果体现为目标car周围开始出现属于背景的虚假信息(如图2(g))，如果C再增大(如C=1.20)这种区域错分将更加严重，分割结果也会变得更为不理想(如图2(h))。

对于其他不同类型的图像，通过大量实验同样可以发现，利用二维斜分MSD法进行阈值分割，随着参数C在一定范围内不断增大，所获得的阈值T*将不断减小，当C值变得很大超过一定范围时这种变化规律将消失而阈值T*会变得很大且不可调节，因此适当选择C值能获得较为理想的分割结果。

3.2 不同阈值选取方法的实验结果比较

为验证二维斜分MSD算法及其快速递推的有效性，对多幅图像进行阈值分割实验，并将分割结果与二维斜分 Otsu 法［10］、二维斜分 MET 法［11］、一维MSD法［9］的进行比较。现选出其中4幅图像Cameraman、Tank、Columbia、Coin 作为示例进行比较说明，这4幅图像都叠加了均值为0、方差为0.01的高斯噪声。对于一维MSD法和二维斜分MSD法，为了能让这两种方法获得较为满意的分割效果，这里将二者的参数C分别设置为C=100，C=1。实验对比结果如图3所示，相应的最佳阈值和运行时间所表2和表3所示。

图3 四种方法分割结果对比

表2 四种方法的最佳阈值比较

表3 四种方法的运行时间比较 单位:s

分割性能效果方面，由图3可以看到，这四种方法中二维斜分MSD法的分割结果更准确、抗噪声能力更稳健，例如Cameraman图像草地上的噪声去除得更加干净;Tank图像中坦克上的轮子和五角星轮廓都更清晰;Columbia图像中尽管建筑物受光照不均但其前面阶梯部分的图像细节仍能保持清晰准确;Coin图像硬币上头像的边缘轮廓更清晰。其余三种方法，一维MSD法的分割结果在图像边缘细节、内部均匀性方面比二维Otsu法的要好，而二维斜分Otsu法在抗噪声方面比一维MSD法的要显著，二维斜分MET法的分割结果和抗噪声能力最不理想。

运行时间方面，分析表3可以看到，三种二维阈值分割方法由于考虑了空间邻域信息，算法复杂性增加，耗时比一维MSD法的要大，但二维斜分MSD法相比二维斜分Otsu法和二维斜分MET法而言花费的时间要少一些，约为它们递推算法运算时间的80% ～90%，可以满足实时处理要求。

4 结论

提出了一种二维直方图区域斜分的最大散度差阈值法，该方法摒弃了一些常用二维阈值分割法中认为二维直方图中反对角线区域概率和近似为零的假设，通过调节参数C改变类间方差和类内方差在分类中的作用，能够在保证去噪效果的同时有效克服二维斜分Otsu法的阈值偏移问题。参数C在一定范围内的不断增大将使得所获阈值T*随之不断减小，在具体应用时对于不同类型的图像，适当选择C值能获得比现有几种常见二维阈值法更准确的图像分割结果。在导出二维斜分MSD法阈值选取公式的同时给出了其快速递推算法，降低了算法复杂性，提升了运算效率。

［1］ Sezgin M，Sankur B.Survey over image thresholding techniques and quantitative performance evaluation［J］.Journal of Electronic Imaging，2004，13(1):146 －165.

［2］ P D Sathya，R Kayalvizhi.Amended bacterial foraging algorithm for multilevel thresholding of magnetic resonace brain images ［J］.Measurement，2011，44(10):1828－1848.

［3］ Yen J C.Chang F J，Chang S Y.A new criterion for automatic multilevel thresholding［J］.IEEE Trans.on Image Processing，1995，4(3):370 －378.

［4］ Jinghao Xue，Yujin Zhang.Ridler and Calvard’s，Kittler and Illingworth’s and Otsu’s methods for image thresholding［J］.Pattern Recognition Letters，2012，33(6):793 －797.

［5］ XU Xiangyang，XU Shengzhou，JIN Lianghai，et al.Characteristic analysis of otsu threshold and its applications［J］.Pattern Recognition Letters，2011，32(7):956－961.

［6］ WU Yiquan，WU Wenyi，PAN Zhe.Minimum within-class variance thresholding based on two-dimensional histogram oblique segmentation［J］.Chinese Journal of Scientific Instrument，2007，29(12):2644 －2655.(in Chinese)吴一全，吴文怡，潘喆.基于二维直方图斜分的最小类内方差阈值分割［J］.仪器仪表学报，2007，29(12):2644－2655.

［7］ CHEN Guo.The fisher criterion function method of image thresholding［J］.Chinese Journal of Scientific Instrument，2003，24(6):564 －567.(in Chinese)陈果.图像阈值分割的Fisher准则函数法［J］.仪器仪表学报，2003，24(6):564 －567.

［8］ SONG Fengxi，CHENG Ke，YANG Jingyu，et al.Maximum scatter difference，large margin linear projection and support vector machines［J］.Acta Automatica Sinica，2004，30(6):890 －896.(in Chinese)宋枫溪，程科，杨静宇，等.最大散度差和大间距线性投影与支持向量机［J］.自动化学报，2004，30(6):890－896.

［9］ WANG Zhibin，GU Yue，LI Zhiquan.Threshold image segmentation based on maximum scatter difference discriminant criterion［J］.Journal of Applied Optics，2010，31(3):403 －405.(in Chinese)王志斌，谷越，李志全.基于最大散度差准则的阈值图像分割［J］.应用光学，2010，31(3):403 －405.

［10］ LIU Jianzhuang，LI Wenqing.Automatic thresholding using the Otsu algorithm based on the two-dimentional grey image［J］.Acta Automatica Sinica，1993，19(1):101 －105.(in Chinese)刘健庄，栗文青.灰度图像的二维Otsu自动阈值分割法［J］.自动化学报，1993，19(1):101 －105.

［11］ ZHANG Xiancheng，SHEN Quntai，WANG Junnian，et al.Application of particle swarm optimization in 2D fuzzy entropy image segmentation［J］.Journal of Chinese Computer Syetems，2008，29(5):959 －962.(in Chinese)张鲜成，申群太，王俊年，等.微粒群算法在二维模糊熵图像分割中的应用［J］.小型微型计算机系统，2008，29(5):959 －962.

［12］ YANG Jinlong，ZHANG Guangnan，LI Shuzhong，et al.Study of image segmentation algorithm based on two-dimensional histogram［J］.Laser ＆ Infrared，2008，38(4):400 －403.(in Chinese)杨金龙，张光南，厉树忠，等.基于二维直方图的图像分割算法研究［J］.激光与红外，2008，38(4):400－403.

［13］ WU Yiquan，PAN Zhe，WU Wenyi.Image thresholding based on two-dimensional histogram oblique segmentation and its fast recurring algorithm［J］.Journal on Communications，2008，29(4):77 －84.(in Chinese)吴一全，潘喆，吴文怡.二维直方图区域斜分阈值分割及快速递推算法［J］.通信学报，2008，29(4):77 －84.

［14］ WU Yiquan，PAN Zhe，WU Wenyi.Maximum entropy image thresholding based on two-dimensional histogram oblique segmentation［J］.PR＆AI，2009，22(1):162 － 168.(in Chinese)吴一全，潘喆，吴文怡.二维直方图区域斜分的最大熵阈值分割算法［J］.模式识别与人工智能，2009，22(1):162－168.

［15］ ZHANG Xinming，LI Zhenyun，SUN Yinjie.Fast image thresholding with minimum error based on 2－d oblique segmentation［J］.Electronics Optics ＆ Control，2012，19(6):8 －12.(in Chinese)张新民，李振云，孙印杰.快速二维直方图斜分最小误差的图像阈值分割［J］.电光与控制，2012，19(6):8－12.