相机标定在瓷砖尺寸检测中的应用

祝文瑾，郭峰林

(武汉轻工大学数学与计算机学院，湖北武汉 430023)

我国的陶瓷墙地砖工业在短短的几十年时间里得到迅速的发展，中国已然成为陶瓷砖生产大国，但国内墙地砖产品的检测技术和检测设备与陶瓷墙地砖现代化生产工艺相比仍明显滞后。基于机器视觉的的瓷砖检测方法，改变了现有的人工检测手段方式精度低，稳定性差等问题。而相机标定技术在机器视觉检测中是必不可少，它是提高系统检测精度的关键所在。本文结合瓷砖检测的特点及要求，提出了一种基于平面网格的相机标定方法。

传统的相机标定方法有直接线性变换方法［1］、Tsai两步法［2］和 zhang 标定方法［3］。直接线性变换法的方便之处在于通过求解线性方程解得到相机的参数，但是忽略了摄像机镜头的非线性畸变。Tsai两步法考虑畸变的影响，并且以直接线性变换方法求得的相机参数作为基础，通过最优化算法进一步提高标定精度。该方法优点是考虑镜头的径向畸变影响同时求解相机内外参数，并且求解过程是线性的，不足之处在:①在高精度测量时，要准确选取优化初值;②只考虑了径向畸变忽略了切向畸变。zhang标定方法特点是需要确定模板上点阵的物理坐标以及图像和模板之间的点的匹配。与传统方法相比zhang标定方法对设备要求不高，操作简单，并且标定精度高，缺点是需要使用者熟悉机器视觉。瓷砖尺寸检测的特点是摄像机和标定板的相对位置固定，属于平面尺寸检测。基于该特点，本文中采用的是基于2D平面靶标的标定方法，将复杂的三维空间标定简化为二维平面标定。该方法使用平面矩形网格作为模板图案，以图格线条交点作为靶标点，标定装置易于制作，标定方法简单易行，完全满足瓷砖检测中对相机标定方法的要求。

1 相机标定的理论基础

照相机成像的几何模型满足空间透视原理，决定了照相机图像上每一点位置和空间相应点之间的相互关系。摄像机几何成像各坐标系转换关系如下。

1)图像物理坐标系与图像像素坐标系之间的转换关系:

式中，(u0，vo)是图像坐标系原点在像素坐标系中的坐标，(x，y)为图像物理坐标系，(u，v)为像素坐标系。像素坐标系在X方向和Y方向相邻两个像素间的距离分别用dx，dy表示。

2)图像物理坐标系与摄像机坐标系转换关系如下:

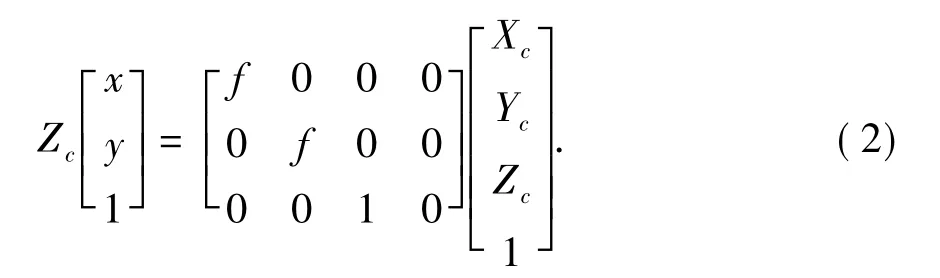
其中f为相机的焦距，(Xc，Yc，Zc)为一空间点 P在相机坐标系中的坐标。

3)摄像机坐标系与世界坐标系转换关系如下:

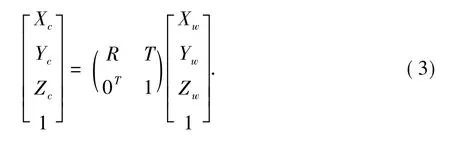
式中，(Xw，Yw，Zw)为空间点P在相机坐标系中的坐标。M称为投影矩阵。R和T是照相机的外部参数，分别表示从世界坐标系到摄像机坐标系的旋转参数矩阵和平移参数矩阵。

2 标定算法

被检测瓷砖的规格为800 mm×800 mm。采用2百万德国映美精DMK 41BF02单色1394工业相机，像素分辨率1 280×960。镜头采用35 mm computer百万像素镜头。

标定算法中采用一种标准的网格模板。网格大小2 mm×2 mm。网格模板放在瓷砖表面，建立相机与网格模板之间的相对位置。精确提取网格交点的像素坐标是采用网格标定板求取摄像机参数一个关键步骤。一般方法是先提取交点附近的四个角点，再由角点坐标的平均得到线条交点的坐标(如图1所示)。摄像机成像时，图像上产生的模糊的过渡带会导致角点坐标获取不准确，影响最后标定结果。

图1 相机标定模型

采用的标定算法:首先提取网格线条边界点，根据提取的边界点来拟合每条边界对应的函数。由拟合的边界函数求网格线条中心线上的离散点的坐标，以这些坐标为基础拟合中心线的函数。对求得的网格线条中心线相互求交即可得到网格线交点，再根据所求的交点像素坐标求得相机参数。计算瓷砖尺寸时，如果采集整块瓷砖的整幅图像，则单位像素所代表的绝对尺寸较大，检测精度达不到生产厂家的要求。采用相对测量方法，分别拍摄被检测瓷砖四个角获取角点坐标，根据标准瓷砖相对应角点坐标信息得到被检测瓷砖尺寸。采用的标定算法具体实现如下。

1)提取每条网格边界对应的边界点

首先用边缘检测算子［4］与待处理像素周围一定范围内的像素点进行加权运算，运算的结果作为是否为边界点的判断依据。提取边界点后，将每个点存储于其对应的边界数组中。

2)边界点拟合曲线

一般线性特征拟合使用的Hough变换与随机采样一致性(RANdomSAmple Consensus，RANSAC)算法，前者适用性广，灵活性强，但存在量化误差和噪声处理的问题，后者能很好的解决前者存在的问题。

使用RANSAC算法来拟合曲线，消除因图像中噪声对边界点提取所带来的影响，从而提高曲线拟合的精度。RANSAC算法的特点是它可以鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数，并能剔除数据集中的少量外点。

3)曲线求交

拟合的为二次曲线，因此必须通解一元四次方程求得曲线交点。为解决该求解过程复杂且耗费时间的问题，在一个小坐标区间内通过直线求交代替曲线求交来获取坐标近似值，该坐标区间为曲线上包含解的一个小坐标区间。

以提取的网格点坐标作为基础，在各网格点位置对网格图像与标准的网格十字图做最小二乘影像匹配［4］。最终的网格点坐标在x、y方向的调整量均在0.1个像素以内，可知通过上述方法提取到的网格点定位精度优于0.1个像素。

4)求解相机内外参数

以网格线向右为x轴，向上为y轴。在网格上确定某个网格点作为空间坐标系原点记为(x0，y0)。提取的网格点对应的网格纵横线引索记为(x，y)。对于每个网格点，其空间坐标表示如下。

为了使空间点的理想位置(ui，vi)与实际成像位置()的距离最小，标定采用基于投影方程的优化方法。设摄像机参数向量为 ξ=(ξ1，...，ξq，p1，p2，k1，k2)T(q≥11) ，其中包含了相机内外参数和各种畸变系数。

最小方差函数如下:

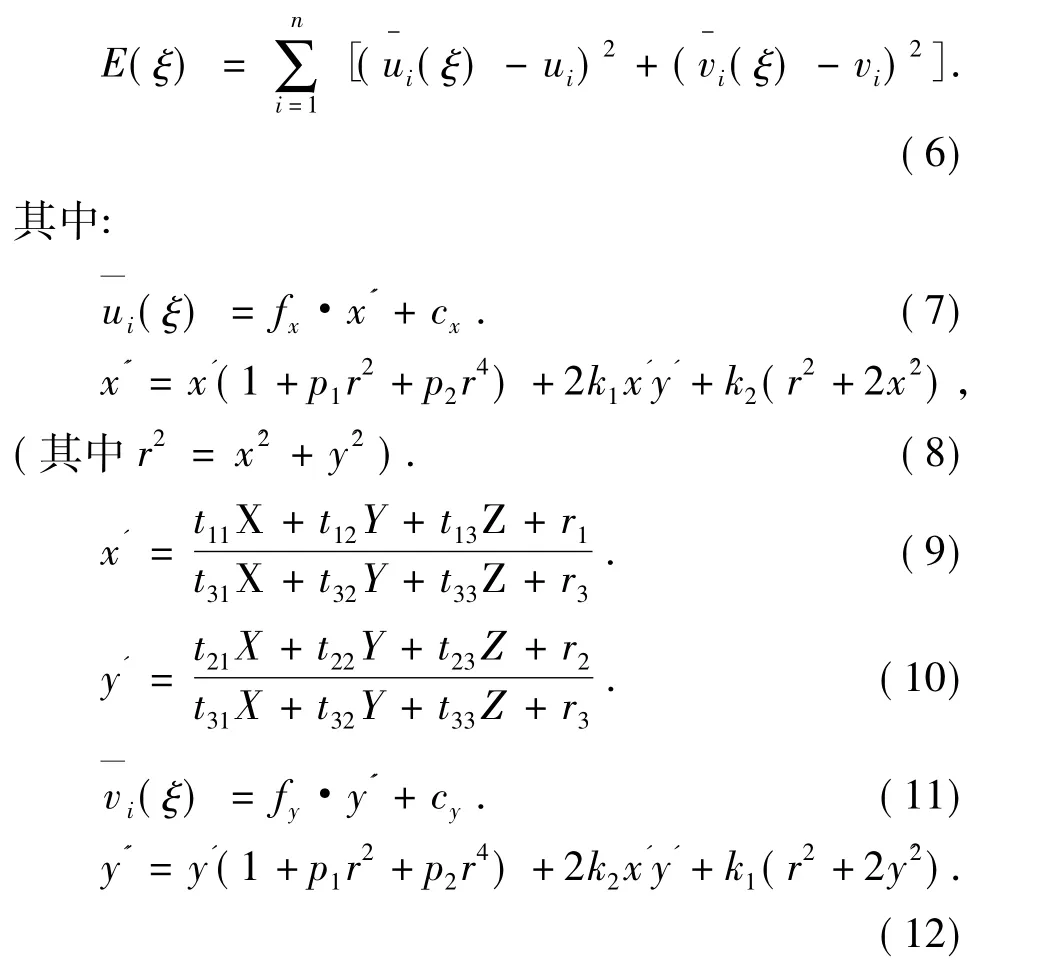
其中:t11，...，t33是旋转矩阵的元素;r1，r2，r3为平移向量元素;p1，p2为径向畸变系数;k1，k2为偏心畸变系数。最小化式(6)是一个非线性最小二乘问题，利用Levenberg-Marquardt算法迭代求解，当||Δξ||小于设定门限时停止迭代，继而得到优化后的相机内外参数［4］。在非线性问题的迭代求解过程中，Levenberg-Marquardt算法解决了高斯牛顿迭代由于Hessian矩阵可能变成奇异阵而导致稳定性较差的问题。Levenberg-Marquardt算法公式描述为:

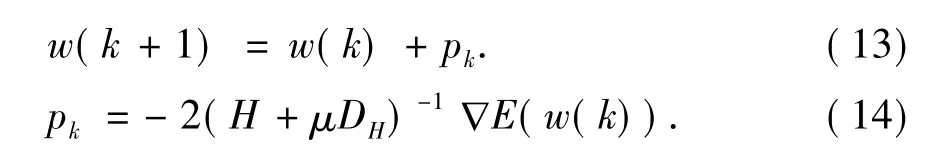
其中:H表示为能量函数E在W(K)处的Hessian阵，DH为对角阵，▽E为E在w(k)的导数阵。

3 标定结果及分析

表1四组数据分别为迭代十次的标定结果，迭代解算时设fx=fy。为了提高像素坐标与三维空间转换的精确度引入畸变系数 k1，k2，p1，p2.。径向畸变p1，p2来自于透镜形状缺陷，产生径向位置的偏差。偏心畸变k1，k2.是指光学中心(光轴与像平面的交点)偏离像平面中心。Ex，Ey分别为图片x，y方向的畸变量，Ep为网格点理想投影位置与实际像点的均方误差。

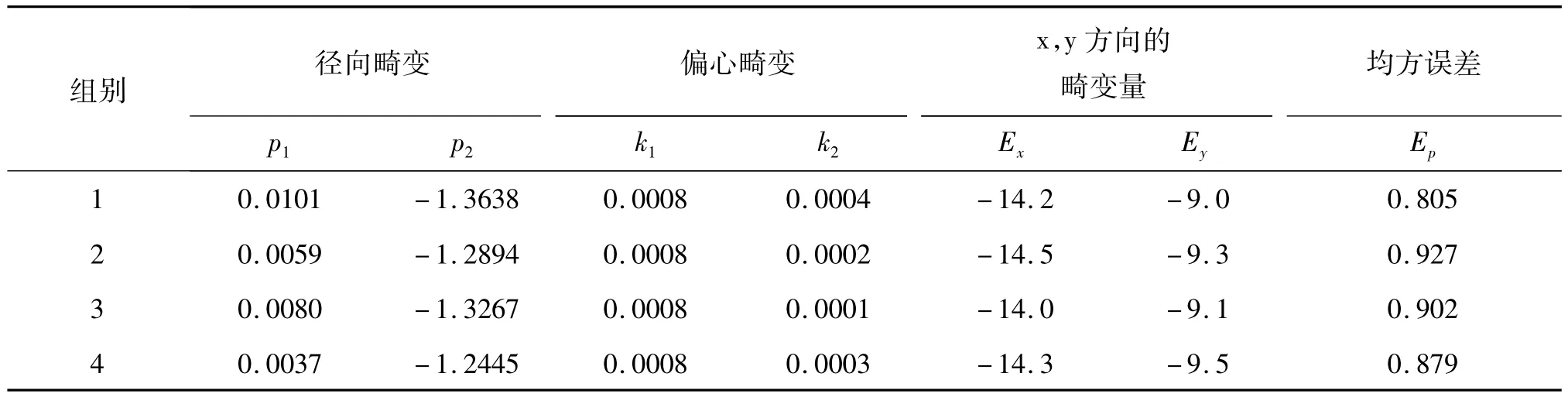
表1 相机标定实验结果

计算公式如下。

实验结果采集了四组数据，其中第一，二组数据中相机与标靶之间距离比第三，四组数据中的略远。通过分析结果可以看出，实验中的重投影均方误差EP控制在1个像素内，解算过程收敛很好，且在迭代6次后结果趋于稳定。畸变量Ex，Ey控制在0.5个像素内，可见畸变系数吻合比较好。畸变是影响视觉测量精度的主要因素，因此该方法能得到可靠稳定的畸变系数。

4 结束语

本文提出的结合相机标定的瓷砖尺寸检测方法有如下特点:①拟合网格线条的方法改进了传统方法中由角点直接求交点过程中模糊过渡带对标定结果精度和稳定的影响，矫正和补偿由于镜头失真和机械安装误差等因素所带来的系统失真;②标定用的靶标制作简单，可稳定、快速的获得较精确地标定结果。实验表明，此方法标定精确度高，不需要人工干预，鲁棒性强，方法简单且稳定性好，适用于瓷砖检测工作。

［1］王东红，罗均，胡釜峰，等.摄像机标定中的直接线性变换法［J］.机械与电子，2006，9(6):9-11.

［2］Tsai R Y.A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses［J］.IEEE Journal of Robotics and Automation，1987，3(4):323-344.

［3］Zhang Z Y.A Flexible new technique for camera calibration［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22(11):1330-1334.

［4］杨阿华，李学军，刘涛，等.基于网格模板的相机标定方法［J］.计算机应用，2013(A01):174-177.