水下突体和声呐导流罩的降噪设计研究

应晓伟

（第七一五研究所，杭州，310023）

现代大、中型水面舰艇艇艏底部大多配置了艇艏探测综合声呐基阵，并使用具有良好声透性的材质与声学特性线型的导流罩加以保护，以提高声呐的信噪比，提高艇艏声呐的探测能力和综合性能。球鼻艏型的声呐导流罩突出于舰艏艇体，在航行时，此类突体附近形成的湍流附面层内介质压力及其质点运动速度存在强烈脉动起伏将引起直接的噪声辐射。作为辐射噪声源之一的水动力噪声，对舰艇总辐射噪声的贡献并不占主要地位，但同时产生的压力起伏，将对置于湍流区的水听器发生作用，使其产生响应，从而增加艇艏声呐的背景噪声，严重影响声呐的输入信噪比。在相同条件下，若自噪声级下降10 dB，则声呐探测距离将增加2～3倍[1]。显然，开展突体线型的流噪声预报研究以及优化突体线型以降低流噪声级的研究具有重要意义。

对于给定的水面及水下航行体突体线型，如果知道可以表征声源强度的表面声功率级，则容易根据其分布状态对其线型进行优化，以达到减阻降噪的目的。本文利用Lilley关于单位体积各向同性湍流流动的声功率公式计算基于NACA翼型的水下突体表面单位声功率级分布，进而探讨水下突体声场随着来流速度和翼型剖面变化的规律，计算某型声呐导流罩的表面单位声功率级分布并根据前面分析的降噪结果对其声学线型优化提出实践的建议。

1 声场计算理论

声源辐射的声功率是声源在单位时间内辐射的总的声能量，用符号Wa表示，单位是W。对只包含某一声源的任何封闭包络面上的垂直声强分量积分，可求得该声源的辐射声功率。实际应用时，将实际的包络面分解成无数单位面积元，积分变为求和从而得到该声源的辐射声功率。对于无方向性的声源，声源级和声源辐射的声功率之间有比较简单的关系，可由声源级 Lpo直接计算出声源辐射声功率 Wa，计算公式为：Lpo=171+10lgWa。因此声功率级可以表征声源的强度。在本文中不对单位面积元上的声功率进行求和，直接计算单位面积元上的声功率级，然后将考虑的突体表面单位声功率级以云图的方式显示，从而可以知道整个水下突体表面产生声源的强度分布。

对于一个各向同性湍流流动，Proudman[2]通过Lighthill声比拟理论推导了其声功率计算公式。近期，Lilley[3]又对其进行了改进，将在Proudman公式中被忽略的延迟时间微分项考虑进去，并得到了单位体积各向同性湍流流动的声功率计算式：

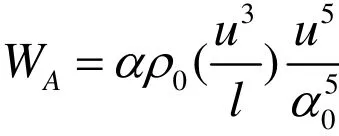
式中：u为湍流速度；l是特征长度；a0为声速；α为模型常数。用k、ε表示为

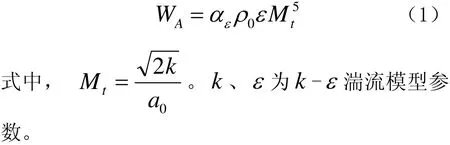
根据Sarkar和Hussaini[4]对于各向同性湍流流动直接数值模拟的标准，aε设为0.1。声功率级的定义为

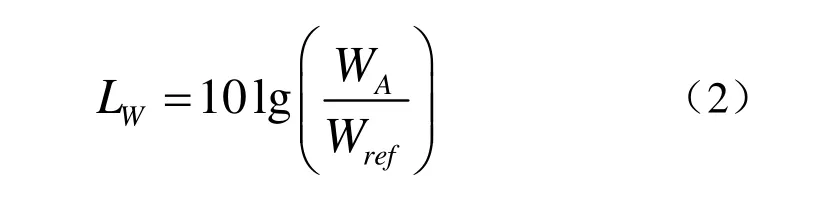
式中，Wref为参考声功率。

从式（1）中还可以看到，Lilley的声功率计算式中有速度变量，对于速度变量的求解本文采用了雷诺平均方法来求解NS方程以得到流场中的速度。

Lilley的宽带声源模型方法给出了湍流流动中声功率级分布的近似计算公式，公式的应用受一些假设的限制：（1）流动必须是各向同性湍流；（2）流动要有较高的雷诺数；（3）流动要有较低的马赫数。

对于水面及水下航行体突体，满足这些假设，可以对其利用宽带声源模型方法估算表面声功率级分布。在对整个模型进行了网格划分和边界条件的设定后开始对声场进行计算。

在本文中设定了隐式、分离式的求解器，选择了雷诺平均的双方程粘性模型。在求解计算时，本文采用了SIMPLEC算法、具有二阶精度的有界中心差分的动量离散格式。在对流场的计算完成后启动宽带声源模型模块对表面声功率级进行计算。

对于水声学，声压以1 μPa为0 dB参考位，应用于各向同性声源。1 W声功率为170.8 dB。

第二次世界大战期间建造的航速为12 kn的水面舰艇，辐射噪声的声源级约为178 dB，这个声源级意味着在半球面范围内，辐射声功率约为2.5 W[1]。

2 水下突体降噪数值研究

试验模型为翼型柱体加顶部回转整流帽，采用四个不同剖面线型的模型，分别为 NACA0009、NACA0012、NACA0015、NACA0020翼型（见图 1），记为 F1、F2、F3、F4，展向高度 l=425 mm，弦长c=500 mm计算域的选取为4000 mm×1200 mm×1000 mm，见图2。

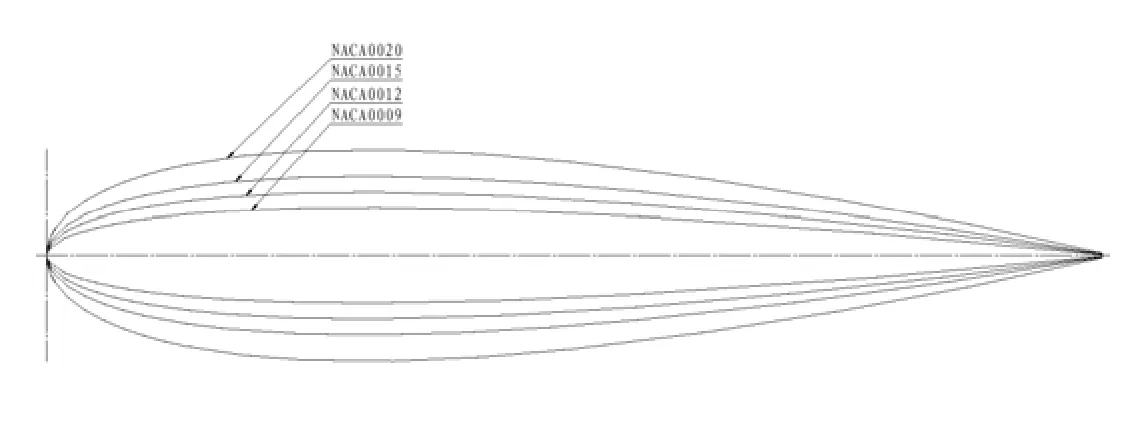
图1 F1-F4机翼线型比较

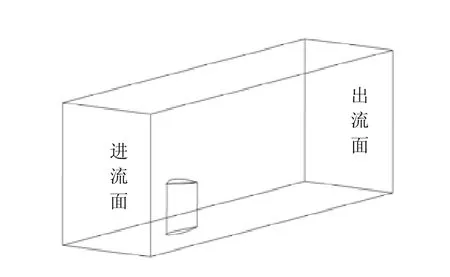
图2 计算域示意图

出于分析不同翼型在不同速度下声场分布的需要，对F1、F2、F3、F4分别计算四个速度，依次为5 m/s、6 m/s、7 m/s、8 m/s，共计算16种情况。

由于模型相对来说是比较复杂的多体组成，因此采用具有良好适应性的非结构四面体网格进行划分，在翼型及其周围部分网格划分比较细密，距翼型距离越远网格尺寸越大。最后网格的最大尺寸为200 mm，最小尺寸仅为10 mm。不同翼型的网格数由表1给出。

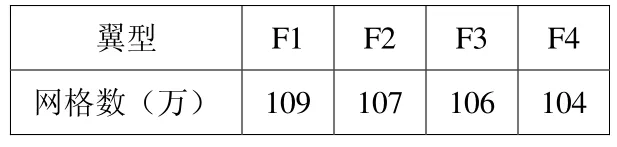
表1 不同翼型的网格数

在计算达到收敛后对计算结果进行分析。在四个翼型表面，静压的变化有着类似的共同点：顺压梯度与逆压梯度的转变发生在翼型最大厚度处。同时在前缘部分，压力的变化剧烈，而在最大厚度后面部分压力分布则趋于平缓。同时，由于翼型剖面的不同，四个翼型也表现出不同的静压分布，总的趋势是从F4到F1，其表面静压分布由变化迅速到趋于平缓。限于篇幅，只给出NACA0020的静压分布。根据Panton[5]的理论，认为具有较大压力梯度的前缘部分其脉动压力越大，从而诱导的流噪声声功率级也越大。

图3 F4静压分布

表面声功率级最大值发生在翼型前缘部分（前缘较亮部分），如图 4所示。很显然由于 F1的前缘半径最小，其有效声源区域的面积也最小，而随着前缘半径的增大声源区域面积也随之增大，在F4时的声源区域面积最大（见图5），可以得出结论：前缘半径的大小决定了声源区域的大小，减小前缘半径可以有效减小声源区面积从而减小流噪声。同时随着翼型表面压力梯度的减小，表面声功率级也随之减小。

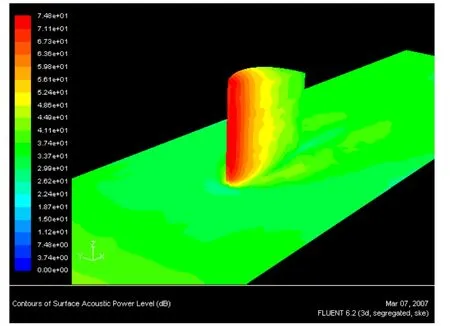
图4 表面声功率级分布

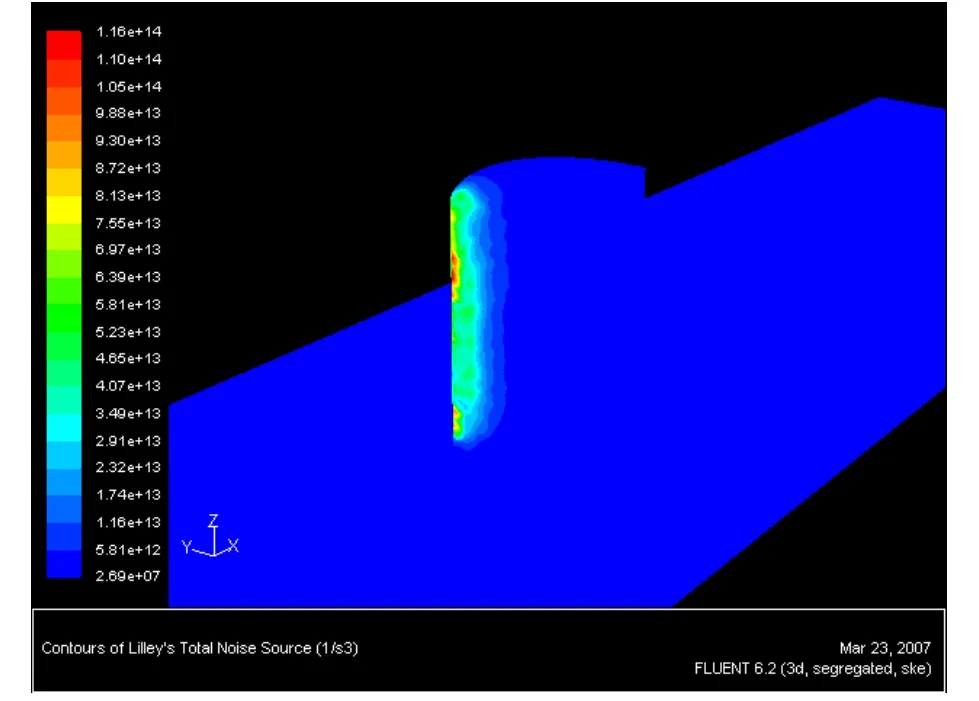
图5 表面声源分布

为了比较不同速度下不同翼型突体的最大声功率级差异，在本文中给出翼型最大声功率级随不同速度与不同翼型的差值，见表2、表3。

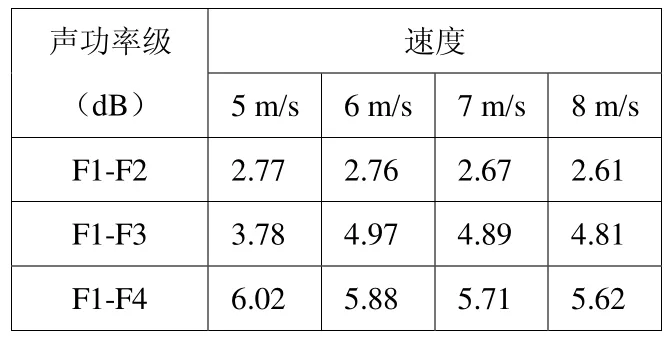
表2 不同翼型在不同速度下声功率级差值

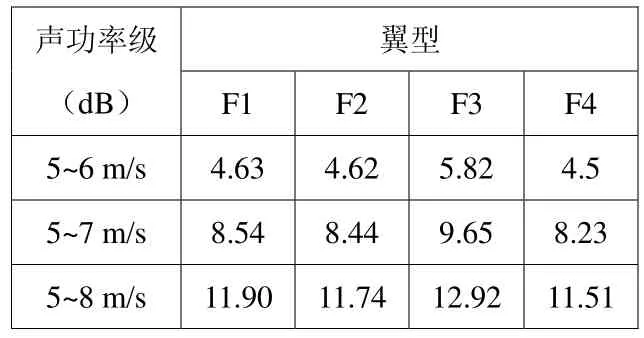
表3 同一翼型在不同速度下声功率级差值

突体的剖面线型，会改变马蹄涡和表面脉动压力的特性，因此影响其流噪声特性，从翼型表面声功率级分布数值计算的结果，可以得到以下结论：

（1）翼型表面声功率级随着来流速度的增大而增大，随翼型厚度和前缘半径的增大而增大。

（2）不同的剖面线型，表面静压分布不同，在表面静压变化剧烈的地方其脉动压力也越大，从而诱导的声功率级也越大。

（3）对于具有水翼线型的突体，其主要噪声源经过计算在翼型的前缘部分，其形状直接影响表面声功率级最大值及其分布。

（4）剖面线型的声学设计，应选取表面静压分布平坦，压力梯度小的线型。采用前缘半径较小，头部较尖锐的翼型可以有效降低突体流噪声；从试验结果可以推测，阻力较低的剖面，其流噪声也较低。

3 导流罩线型声场数值分析

球艏型导流罩安装在舰船艏部，并且与舰船上部线型光顺过渡。作为球艏的一部分，导流罩还起到减小舰船兴波阻力的作用。而作为减小声呐自噪声的主要结构，导流罩起了很大作用。导流罩一般都制作成流线型，在其表面水流光滑流过，在前一章的分析中知道，表面静压梯度小的水下突体线型其诱导的声功率级小，因此导流罩的主要作用在于使流动的静压分布平缓，并且避免水流直接作用于声呐基阵，从而减小声呐自噪声的干扰。

由于只是对导流罩附近的流场感兴趣，同时为了尽量真实地模拟舰船水下部分的流场，本文中采用船型前部到第5站的水下部分建立模型。

对于计算域的划分，由于直接关系到网格划分的数目进而影响计算速度，为了在不使模拟的流场失真的前提下达到最快的计算速度，综合考虑后本文中的计算域采用42000 mm×20000 mm×12600 mm的长方体，如图6。

图6 计算模型

在对网格进行划分的时候，由于只关心导流罩附近的流场，本文在导流罩附近的网格划分较密，随着与导流罩距离的增大网格尺寸也相应增大。本文同时计算了速度为28 kn时模型在不同网格数下的声场以讨论网格数对计算的影响，其结果如图 7所示，从图中可以看出当网格数较小时计算所得的声功率级起伏较大，随着网格数的增加，计算值也趋于稳定，综合考虑计算速度和精度后，本文最终采用的网格划分最小尺寸为150 mm，最大尺寸为2000 mm，增长率为1.03，最终的网格数为138万。

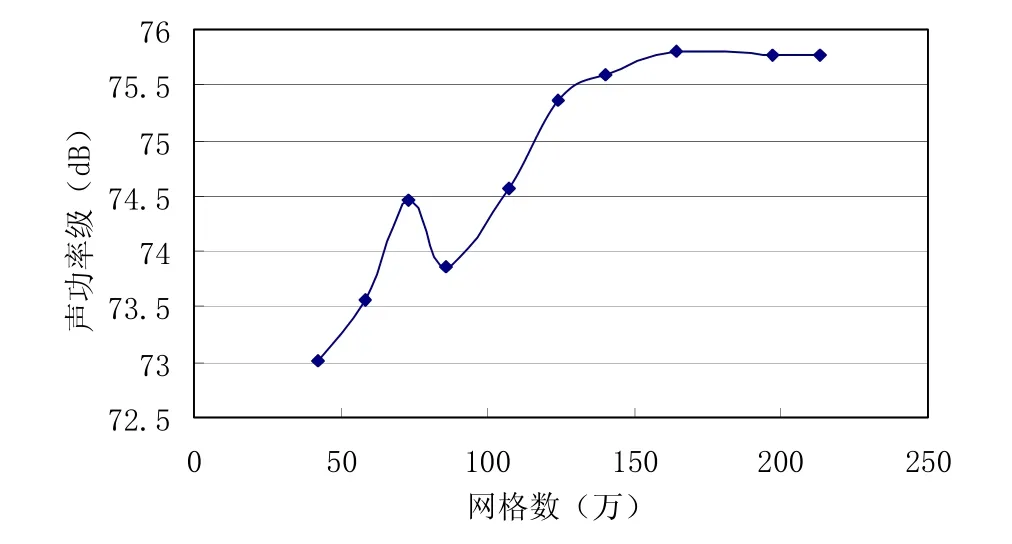
图7 网格数变化对计算的影响

具体表面声功率级计算过程与前面水下突体声功率级相同，这里不再赘述，直接对结果进行分析。从图8中可以看到，在导流罩的前缘，静压分布变化剧烈，在导流罩剖面的最大半径处流动从顺压梯度转变为逆压梯度，压力变化非常剧烈。通过计算所得的声源分布云图(图 9)，在球艏与上部船体连接处声源强度达到最大值（图中最亮部分），同时可以注意到在静压分布云图中也是上部船体与球艏的连接处压力变化最剧烈，这与Panton[5]的理论相符合。但是从声功率级分布云图可以看出导流罩整个前缘部分都具有较大的声功率级，其幅值与导流罩和上部船体连接处的最大幅值接近，这也是声呐基阵的主要布置位置，减小整个前缘部分的声功率级就能减小整个导流罩的声功率级从而使设置在此处的声呐基阵的自噪声减小并达到更远的探测距离。

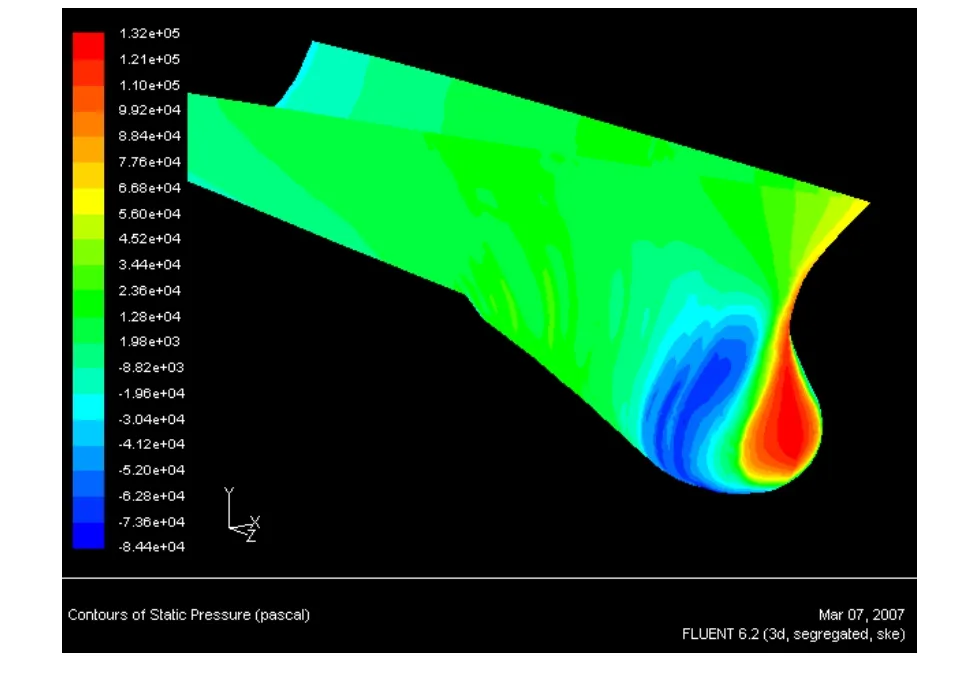
图8 导流罩表面静压分布

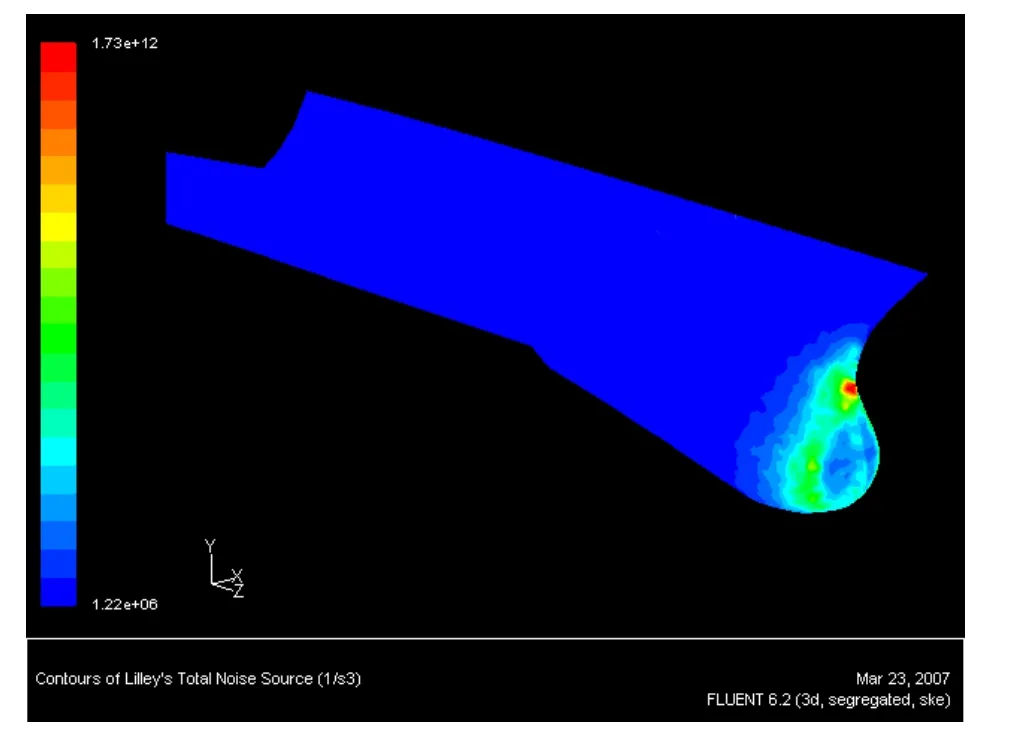
图9 导流罩表面声源分布

通过研究分析，以及根据Panton[5]的理论和前面章节的计算与分析，本文认为选择前缘剖面半径较小的导流罩线型，即考虑声呐布置的情况下采用“修长型”的导流罩线型有利于使表面静压分布趋于平缓从而减小表面声功率级，在导流罩的声学优化设计当中这是一个方向。

4 结论

通过对导流罩表面声功率级分布的分析发现球鼻艏型导流罩表面声功率级的最大值发生在球鼻艏的前缘部分，同时通过分析提出采用减小导流罩前缘剖面半径使导流罩更加“修长”的办法来减小前缘声功率级，其有效性还需要试验结果的验证。应用此方法法进行导流罩线型声学优化设计可以作为进一步的研究方向，其计算方法和导流罩线型的声功率级分布图可作为线型优化设计的参考。

[1]王之程, 陈宗岐, 于沨, 等. 舰船噪声测量与分析[M].北京：国防工业出版社, 2004:1-4.

[2]PROUDMAN I. The generation of noise by isotropic turbulence[J]. Proc.Roy.Soc., 1952, A214: 119.

[3]LILLEY G M. The radiated noise from isotropic turbulence revis-sited [R]. NASA Langley Research Center,Hampton, VA,1993.

[4]SARKAR S, HUSSAINI M Y. Computation of the sound genetated by isotropic turbulence[R]. NASA Contract Report93-74, NASA Langley Research Center, Hampton,VA, 1993.

[5]PANTON R L, LINEBARGER J H. Wall pressure spectra calculation for equilibrium boundary layers[J]. J Fluid Mech, 1974,65(2): 261-287