一种甚低频正弦振动系统的运动学仿真

朱学文 陈毅

（第七一五研究所，杭州，310023）

海洋中传播着各种不同频率的声波，有高频声波、低频声波以及由海洋运动、地震等引起的甚低频声波。为了海洋开发、气候研究的需要，就必须对海洋中的声信号进行检测，而检测之前必须对检测水听器进行预先校准。基于对该频段水听器校准的需要，我所建立了0.01～1 Hz水声声压计量标准装置 [1]。本文就是以SolidWorks软件为建模平台，对该标准装置中的振动机构进行三维建模、虚拟装配和虚拟样机仿真[2]，以验证对称锥齿轮差速机构原理的准确性和振动系统的可行性，为该装置的后续改进提供帮助。

1 标准装置的组成

标准装置由3部分组成：一是声压生成系统，由测量水腔、振动容器和连通管组成；二是正弦振动系统，由双通道函数发生器和正弦振动机构组成；三是电子测量与控制系统，由前置放大器、滤波器、低频电压测量仪、示波器、计算机及外设组成[1]。其中正弦振动系统原理框图如图1所示。

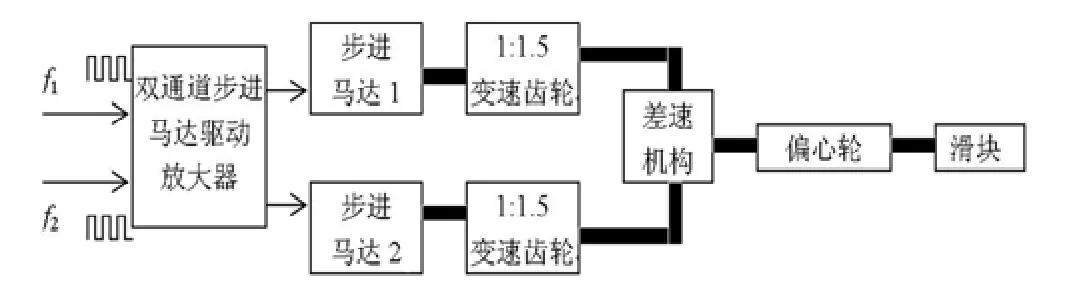
图1 正弦振动系统原理框图

来自双通道函数发生器的两个信号频率分别为f1和f2，输入至双通道步进驱动放大器的相应通道，经放大后，分别以频率 f1的脉冲电流驱动步进电机1，以频率f2的脉冲电流驱动步进电机2。两个步进电机是同型号的，同时各自驱动一个1:1.5的变速齿轮，这两个变速齿轮同时啮合至一个锥齿轮差速机构。此差速机构的输出轴能带动一个偏心轮回转，而偏心轮可以带动一滑块上下运动，通过它把回转运动转换成垂直直线简谐运动，偏心轮回转一周，形成一个周期的垂直直线简谐运动。采用双步进电机差动输出的目的是为了保证振动系统的平稳。标准装置的方案确定以后，使用三维建模软件SolidWorks对系统进行三维建模和虚拟装配，其中正弦振动机构的俯视图三维模型以及正弦振动组件的三维模型分别如图2和图3所示。

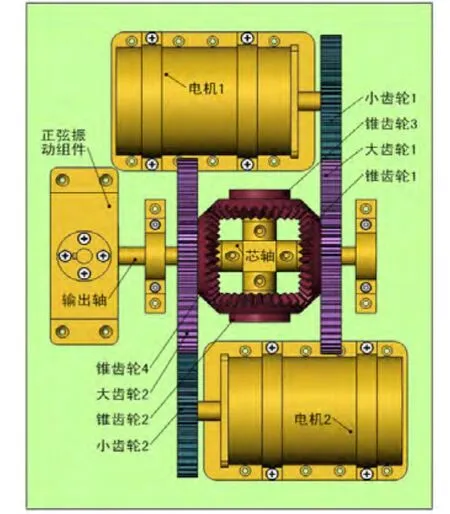
图2 正弦振动机构俯视图

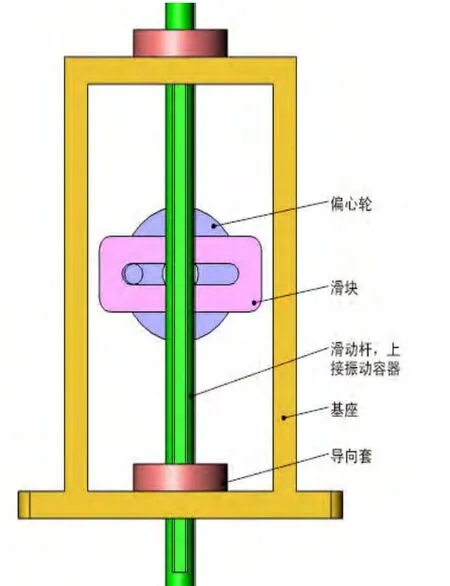
图3 正弦振动组件

2 正弦振动机构运动学仿真

2.1 运动学仿真概述

机构的运动学分析就是根据原动件的已知运动规律，来确定其它构件或构件上某些点的位移、速度和加速度等运动参数。通过机构的位移分析，可以确定机构运动所需空间或构件及构件上某些点能否实现预定的位置或者轨迹，并可以判定它们在运动中是否发生干涉；通过速度、加速度分析，可以了解从动件的运动变化规律能否满足工作要求，并可据此对机构进行动力学分析。

机构运动学仿真分为以下几个步骤：（1）创建零件模型，使用各种特征创建工具创建零件模型；（2）组装零件模型，使用装配命令，组装零件模型，生成连接；（3）运动仿真参数设置，按照产品要求进行运动定义；（4）仿真结果分析，对仿真结果进行分析保存。

2.2 正弦振动机构的运动学理论分析

按照图1所示流程，设步进电机1频率f1＝50 Hz，步进电机2频率f2＝100 Hz，两步进电机型号相同，它们与驱动器相配都接成Δθ=0.9°/步的步进间距，则两电机转速分别为45 deg/s与90 deg/s（与仿真参数设置相同），两步进电机同时各自驱动一个 1:1.5的变速齿轮，则这两个变速齿轮的角速度分别为：

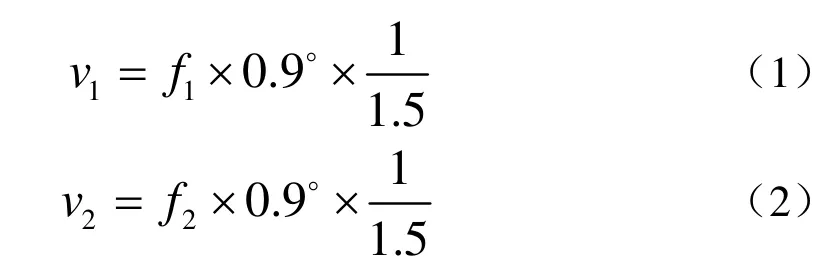
它们同时啮合至一个差速机构。此差速机构设计成能带动一个具有偏心栓子的回转轮以

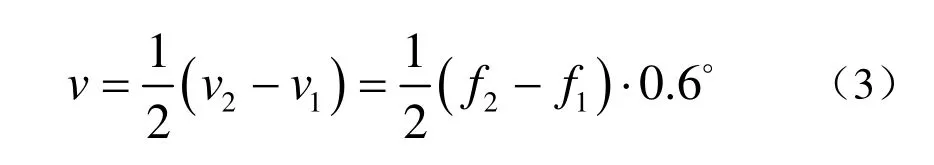
的角速度回转，偏心轮可以带动一滑块上下运动，通过它把回转运动转换成垂直直线简谐运动，偏心轮回转一周，形成一个周期的垂直直线简谐运动。

因此，与步进马达的驱动脉冲频率联系起来，就可以得到垂直直线简谐运动的频率为：

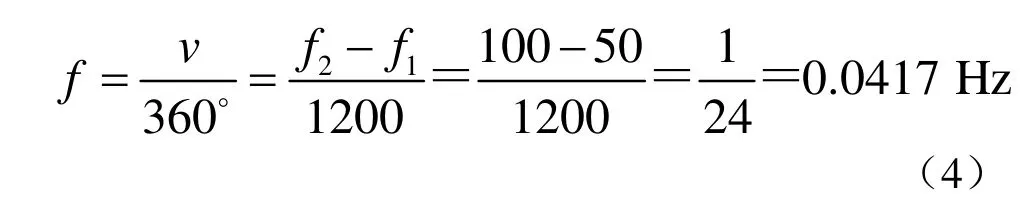
2.3 仿真参数设置

虚拟装配完成后，在小齿轮与电机之间、大齿轮与输出轴之间、锥齿轮与芯轴之间分别设置旋转副，在电机1与小齿轮1之间的旋转副上设置运动常数为−45 deg/s，在电机2与小齿轮2之间的旋转副上设置运动常数为90 deg/s，其中“−”表示二者转动方向相反；在滑块与基座（大地）之间设置移动副；在两对大小齿轮之间、4个锥齿轮两两之间添加3D碰撞约束，3D碰撞约束常用于齿轮类、凸轮类零件之间的碰撞接触，不允许零件之间相互穿透。3D碰撞约束参数设置如图4所示。设置仿真时间为24 s，帧数为200帧。设置完成后运行仿真。

图4 3D碰撞约束参数设置

2.4 仿真结论分析

由以上设置可知，电机1与电机2的输出轴转速分别为−45 deg/s与90 deg/s，则根据大小齿轮齿数比可知，大齿轮1与大齿轮2的转速分别为−30 deg/s与60 deg/s，根据锥齿轮差速机构原理，则输出轴的转速 n应为二者代数和的一半[3]，即：n=（−30+60）/2=15 deg/s，输出轴转动一周 360°需要24 s，即一个回转周期为24 s。同理，因为输出轴与偏心轮的角速度一致，所以由偏心轮带动滑块所形成的垂直直线简谐振动周期也是24 s。

根据仿真结果，提取输出轴转动的角速度曲线如图5所示，提取滑块垂直简谐振动的曲线如图6所示。由图5可以看出，输出轴的角速度在15 deg/s附近上下波动，角速度大小与理论计算相符，数值波动情况与齿轮之间3D碰撞设置参数有关。由图 6可以明显看出，滑块振动为简谐振动，其曲线为平滑的余弦曲线，振动周期为24 s，与理论分析得出的结论一致，也直接证明简谐振动机构的可行性。

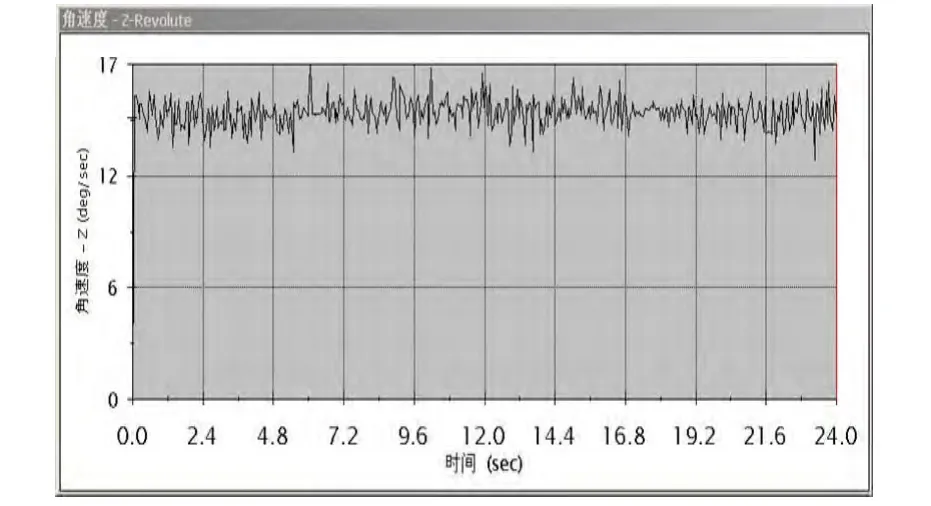
图5 输出轴角速度曲线

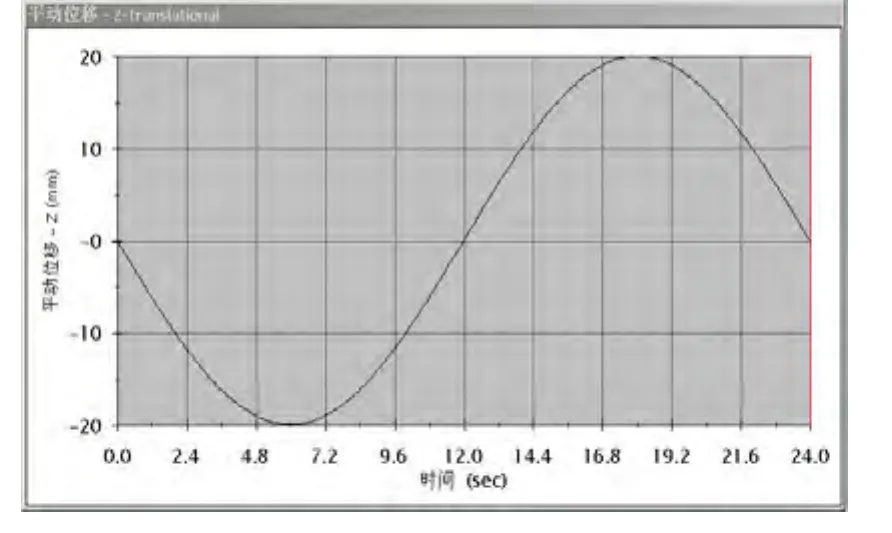
图6 简谐振动曲线

3 结论

本文针对0.01～1 Hz水声声压标准装置中的正弦振动系统，以Solidworks软件为建模平台，组建了锥齿轮差速机构，并利用Solidworks运动仿真插件 COSMOSMotion进行运动学仿真，经过运动仿真，可以看出仿真结果与理论分析计算结果吻合的很好，从侧面印证了锥齿轮差速机构原理的准确性，也证明了简谐振动机构的可行性，为该机构的后续应用和改进奠定基础。

[1]袁文俊. 0.01～1Hz水声声压标准装置的研究[J].计量学报, 2004,(3): 270-274.

[2]二代龙震工作室. Solidworks+Motion+Simulation建模/机构/结构综合实训教程. 北京: 清华大学出版社, 2009.

[3]张晓岚, 陈卫华. 0.01～1Hz水声声压计量标准装置中的振动机构设计[J]. 计量与测试技术, 2001, 28(4).