压电圆管换能器静态电容与测量温度相关性分析

张存发

(山西汾西重工有限责任公司，太原，030027)

随着水声技术的深入发展，水声换能器的低频灵敏度以及阻抗匹配特性，得到了越来越广泛的关注。在低频工作状态下，换能器的静态电容直接影响换能器的低频灵敏度特性和阻抗匹配特性。因此对于换能器设计者来说，在某些情况下，必须控制低频换能器的静态电容使其低频灵敏度特性、阻抗匹配特性满足设计指标要求[1]。

本文通过对压电陶瓷圆管静态电容与测量温度的相关性分析[2]，导出了在不同测量温度时，压电陶瓷圆管静态电容测量误差的控制范围，以确定在不同测量温度时压电陶瓷圆管静态电容最佳的最小值的计算方法。

1 相关系数的计算方法

考虑到数值按比例缩小相同的倍数后，对相关性分析没有影响，为了计算方便，以下分析计算按实际测量值缩小100倍。假设实际的测量样本值为N=4600，则计算中的n=4600/100=46。

1.1 计算偏差平方和Sxx,Syy,Sxy的值

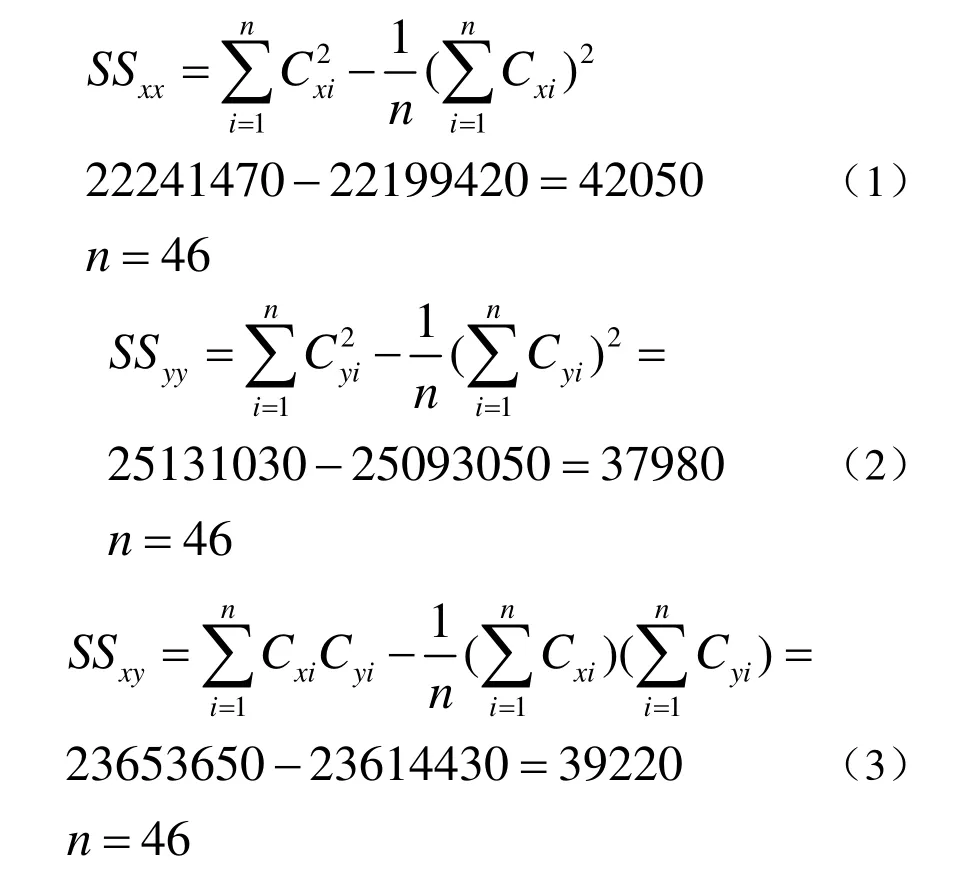
式中，Sxx为因素x引起的偏差平方和；Syy是因素y引起的偏差平方和；Sxy为因素 x、y共同引起的偏差平方和；Cxi为因素 x对应的第 i个的电容；Cyi为因素y对应的第i个的电容。

1.2 计算相关系数r

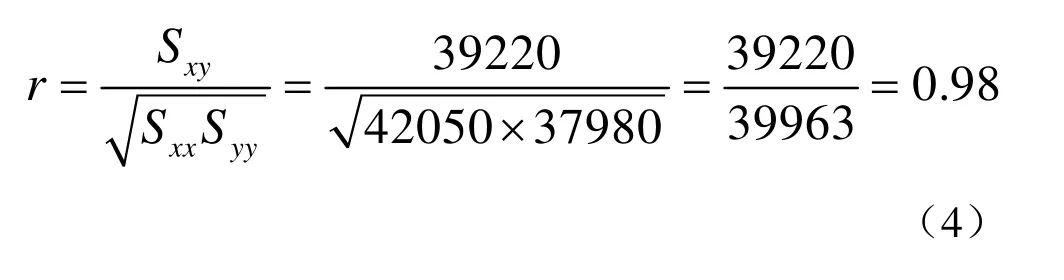
2 分布图与相关情况分析

2.1 典型图例法

将压电陶瓷圆管静态电容与测量温度散布图（图1）与典型图例比较可以看出： 压电陶瓷圆管静态电容与测量温度正相关。

图1 压电陶瓷圆管静态电容与测量温度散布图

2.2 象限判断法

因为： n1+ n3= 21+ 21 = 42

n2+ n4= 2 + 2 = 4

所以： n1+ n3＞n2+ n4

由此可知压电陶瓷圆管静态电容与测量温度正相关。

2.3 相关系数判断法

由1.2节的计算可知相关系数r = 0.98，根据相关情况判别式：为强相关，现在相关系数r =0.98，所以压电陶瓷圆管静态电容与测量温度两变量之间为正强相关关系。

三种判断法得出的结论是一致的，压电陶瓷圆管静态电容与测量温度之间存在正强线性相关关系。

2.4 相关系数的检验

由显著性水平 α= 0.05 和α= 0.01、自由度f =n–2 = 46–2=44 查表可得：r0.05= 0.288、r0.01=0.372。计算 r=0.98，则有，所以压电陶瓷圆管静态电容与测量温度两变量之间有着高度显著的线性相关关系，因此可以求得有效的一元线性回归方程：ˆy=a+bx（其中a、b为方程的未知参数）。

3 预测和控制

3.1 求解回归方程

3.2 预测区间半径δ

3.3 预测区间中点

x0=694.7，置信水平：1−α=0.95

预测区间：

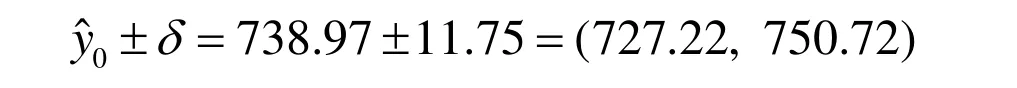
3.4 压电陶瓷圆管静态电容下限的控制

为了使换能器静态电容在测量温度为 15℃时仍满足技术指标Cxmin≥650 pF的要求，在测量温度为 25℃时，必须对其压电陶瓷管静态电容Cymin进行下限控制。因产品对其静态电容上限没有要求，静态电容值越大越好。因此我们只对压电陶瓷管静态电容的下限进行控制。

求解回归方程可得：Cymin=bCxmin−δ+a

根据以上分析和换能器技术条件要求，在测量温度为15℃时，必须使压电陶瓷管静态电容值Cxmin≥650 pF。

取Cxmin＝650 pF计算在测量温度为25℃时压电陶瓷管静态电容值。

则 Cymin=0.93×650−11.75+92.9=685.65（缩小100倍计算值）

通过以上分析可知，在不考虑其它因素影响的情况下，为了保证换能器静态电容在测量温度为15℃时仍满足技术指标的要求，在装配前，当测量温度为25℃时，压电陶瓷圆管静态电容的最小值为68565 pF（实际要求值），考虑到其他因素的影响建议取Cymin≥70000 pF（见表1：压电陶瓷圆管静态电容值统计表。附文后）。

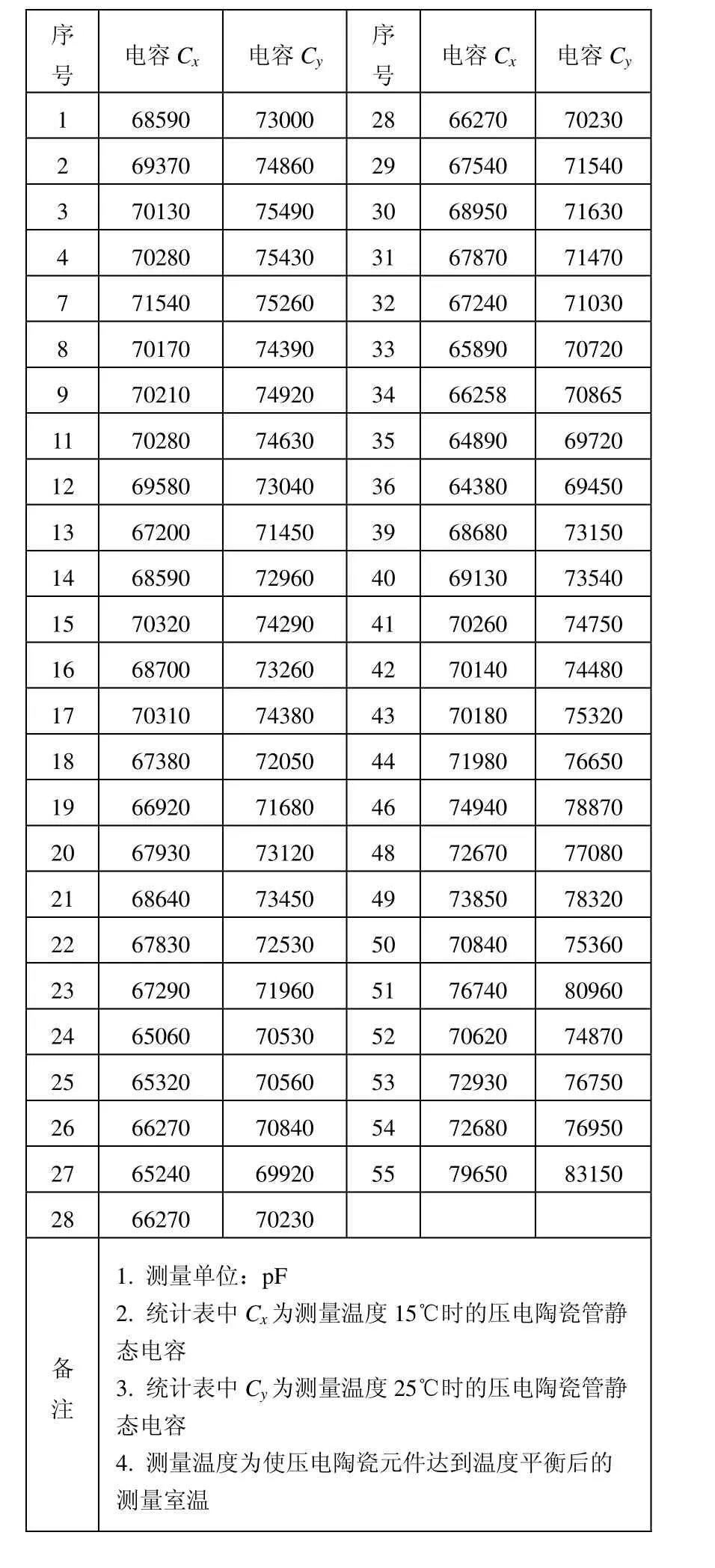
表1 压电陶瓷圆管静态电容值统计表

4 结论

● 压电陶瓷圆管静态电容与其测量温度之间存在着正线性相关关系。

● 根据产品技术条件对换能器静态电容的技术要求，用解回归方程的方法，可完成对压电陶瓷圆管静态电容在不同测量温度时的筛选控制。

● 压电陶瓷圆管换能器的静态电容值，与测量温度同样存在着正强线性相关关系。因此在换能器设计技术要求中规定静态电容值时，必须明确规定测量温度，否则将导致严重的测量误差。

[1]栾桂冬, 张金铎, 王仁乾. 压电换能器和换能器阵[M].北京: 北京大学出版社, 2005.

[2]盛骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京:高等教育出版社,1989.