例谈坐标法解决平面向量中的求值问题
林丽虹

【摘要】平面向量的表示方法有几何法和坐标法.向量的表示不同,对运算也会产生不一样的结果.在解题中,如果能够结合题目的实际情况,机智地作出选择,选择恰当的方法,对问题的解决事半功倍.
【关键词】平面向量;坐标法;平面直角坐标系
平面向量中的最值与范围问题是一个热点,也是一个难点,这类问题的题型是根据已知条件求某个量的最值、范围,如模、夹角、系数数量积等,解决这一类问题的关键是建立求解目标的函数关系式,通过函数的值域解决问题,而平面向量兼顾“数”与“形”的双重身份,所以解决这类问题的一種基本思想就是数形结合.而坐标法作为实现平面向量几何问题代数化的一种体现,所以有必要对坐标法在向量中的应用做进一步的研究.
坐标法是通过建立直角坐标系,把几何问题转化为代数问题,使得向量的运算完全代数化的一种方法.本文主要是结合近几年的各地高考题模拟题来说明坐标法的应用.那么什么样的题目适合用坐标法呢?如题目中,已经有些元素被量化了,如有直角、 有长度、有角度等,那么是不是可以考虑选择坐标法来解决问题.
高考试卷、模拟卷等经常会有一些向量的应用的题目,特别是求值、求最值问题往往难度都比较大,但是如果能够根据条件,适当建立直角坐标系,则问题即可迎刃而解.如本文根据近两年常遇到的一些质检题、高考题,谈谈关于坐标法在解决平面向量中的最值问题的一些应用.
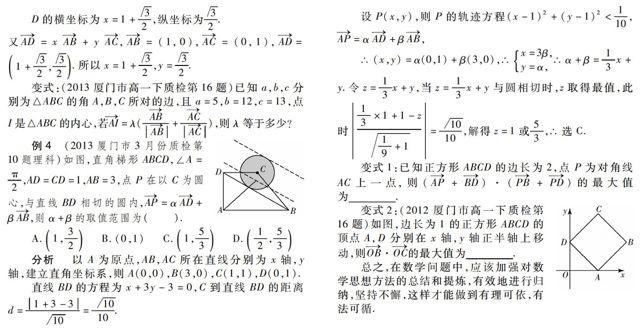
例1 (2013福建省质检8)在矩形ABCD中,AB=1,AD=3,P为矩形内一点,且AP=32,若AP=λAB+μAD,λ,μ∈R,则λ+3μ的最大值为( ).
A.32B.62
C.3+34D.6+324
分析 如图,建立平面直角坐标系,则A (0,0),
B(0,1),C(3,1),D(3,1).
设P(x,y),则x2+y2≤34(0≤x≤3,0≤y≤1),AP=(x,y)=λ(0,1)+μ(3,0).
∴x=3μ,
y=λ.所以λ+3μ=x+y,转化为线性规划问题,可行与域为四分之一圆
当直线z=x+y与圆x2+y2=34相切时,z最大,即0+0-z2=32,又z>0,∴z=62.选B.
例2 (2009安徽理数)给定两个长度为1的平面向量OA和OB,它们的夹角为120°,点C在以圆O为圆心的圆弧OA上变动,若OC=xOA+yOB(x,y∈R),则x+y的最大值是.
分析 以O为原点,OA所在直线为x轴,过O垂直于OA的直线为y轴,建立平面直角坐标系,则A(1,0),B-12,32,Cx-12y,32y.
因为点C在以圆O为圆心的圆弧OA上变动,所以C(cosθ,sinθ),其中0≤θ≤2π3.
所以x-12y=cosθ,
32y=sinθ,解得x=cosθ+3sinθ3,
y=23sinθ3.
所以x+y=cosθ+3sinθ=2sinθ+π6≤2,
当且仅当θ=π3时等号成立.所以x+y的最大值是2.
例3 如图,两块斜边长相等的直角三角板拼在一起,∠ACB=45°,∠DEB=60°,若AD=xAB+yAC,则x=,y=.
分析 以A为原点,建立直角坐标系,如图所示.
设AB=AC=1BC=DE=2.
∵∠DEB=60°,∴BD=62.
由∠DBF=45°,解得DF=BF=62×22=32,
D的横坐标为x=1+32,纵坐标为32.
又AD=xAB+yAC,AB=(1,0),AC=(0,1),AD=1+32,32.
所以x=1+32,y=32.
变式:(2013厦门市高一下质检第16题)已知a,b,c分别为△ABC的角A,B,C所对的边,且a=5,b=12,
c=13,点I是△ABC的内心,若AI=λ(ABAB+ACAC),则λ等于多少?
例4 (2013厦门市3月份质检第10题理科)如图,直角梯形ABCD,∠A=π2,AD=CD=1,AB=3,点P在以C为圆心,与直线BD相切的圆内,AP=αAD+βAB,则α+β的取值范围为( ).
A.1,32 B.(0,1)
C.1,53 D.12,53
分析 以A为原点,AB,AC所在直线分别为x轴,y轴,建立直角坐标系,
则A(0,0),B(3,0),C(1,1),D(0,1).
直线BD的方程为x+3y-3=0,C到直线BD的距离d=1+3-310=1010.
设P(x,y),则P的轨迹方程(x-1)2+(y-1)2<110, AP=αAD+βAB,
∴(x,y)=α(0,1)+β(3,0),∴x=3β,
y=α,∴α+β=13x+y.令z=13x+y,当z=13x+y与圆相切时,z取得最值,此时13×1+1-z19+1=1010,解得z=1或53,∴选C.
变式1:已知正方形ABCD的边长为2,点P为对角线AC上一点,则(AP+BD)·(PB+PD)的最大值为.
变式2:(2012厦门市高一下质检第16题)如图,边长为1的正方形
ABCD的顶点A,D分别在x轴,y轴正半轴上移动,则OB·OC
的最大值为.
总之,在数学问题中,应该加强对数学思想方法的总结和提炼,有效地进行归纳,坚持不懈,这样才能做到有理可依,有法可循.

