FLiBe、FLiNaK在涡流二极管中流动特性的数值模拟

戴悦来 戴志敏 吴燕华

1（中国科学院上海应用物理研究所 嘉定园区 上海 201800）

2（中国科学院大学 北京 100049）

熔盐堆作为六种先进四代堆型之一，在固有安全、燃料循环、小型化、核资源的有效利用和防止核扩散等方面有其特有的优点。2011年中国科学院启动实施了“未来先进核裂变能——钍基熔盐堆核能系统” (Thorium Molten Salt Reactor, TMSR)战略性先导科技专项，由中国科学院上海应用物理研究所承担，其中TMSR池式反应堆辅助冷却系统(Pool Reactor Auxiliary Cooling System, PRACS)在反应堆设计和运行中占据重要地位，确保反应堆事故工况下堆芯余热的顺利导出，涡流二极管泵装置作为一种无传动装置的新型免维修设备，以其固有的内在特性，被引入 PRACS的概念设计中。美国橡树岭国家实验室初步完成对涡流二极管应用于高温熔盐堆(Fluoride salt-cooled High temperature Reactors，FHRs)专用辅助冷却系统(Dedicated Reactor Auxiliary Cooling System, DRACS)的概念设计[1]。

在20世纪80年代涡流二极管开始用于核工业后处理工厂的乏燃料输送，其基本原理为流体工质正反向通过涡流二极管时，反向压降值明显高于正向压降值，具有不同的阻力系数[2]，类似于电路中“二极管”的作用。其中，反向流动时，内部流场表现为复杂的三维强剪切湍流场，与旋风分离器、水力旋流器、涡流放大器等流体控制设备类似。

本文对 PRACS中的涡流二极管装置进行初步分析，为进一步改进和优化熔盐堆辅助冷却系统的设计提供参考。首先建立涡流二极管模型，采用FLUENT软件模拟在不同工况条件下的涡流二极管正反向流阻及性能参数，并通过改进其结构达到优化的目的，再结合实验进一步验证。

1 分析模型

1.1 系统描述

TMSR池式反应堆辅助冷却系统中的 DRACS部分由换热器、涡流二极管及相关管道组成，系统示意图如图1。

图1 TMSR池式反应堆Fig.1 Pool reactor of TMSR.

在正常工况下，涡流二极管处于反向流动状态，流阻高，起到隔阻的作用；在非正常工况下，主泵停止工作，此时，一回路进入自然循环状态，管道内熔盐工质开始反向流动，涡流二极管转变成正向流动状态，流阻低，保证堆芯余热顺利导出。

1.2 涡流二极管模型

涡流二极管由切向管、旋流腔、轴向管三部分组成。其工作模式：当流体从切向管流入腔室时，由于切向管的收缩作用，流体工质以射流形态进入涡流腔，在壁面作用下形成旋流，从而产生较大的流阻，称为反向流动；而当流体工质从中心管流入时，流动相对简单，无大的旋流产生，流阻相对小，称为正向流动。衡量涡流二极管性能指标参数：阻力系数x(或欧拉数Eu)与阻抗比e：

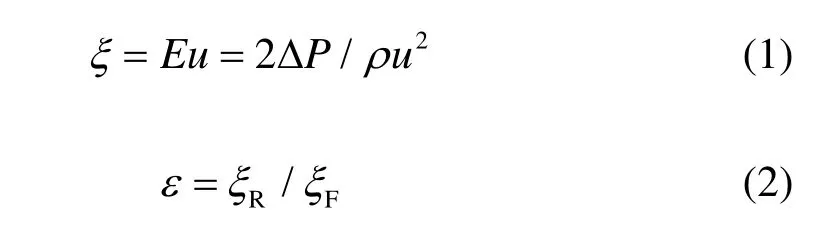
涡流二极管的雷诺数计算公式：

式中，V、d为切向管与腔室连接处的速度、管径；r、m为工质的密度和粘度。

1.3 模拟计算前处理

涡流二极管模型采用 SolidEgde软件进行几何建模，前处理在ICEM上进行，采用结构化网格与非结构化网格相结合的混合网格，腔室与切向管连接处为四面体网格，其余部分为六面体网格，网格质量较好，网格总数在80余万。模型示意图见图2。

图2 涡流二极管模型Fig.2 Model of vortex diode.

1.4 模拟条件设置

方程的求解在 FLUENT6.3上进行，由于二极管内部工质的温度变化很小，因此忽略温度场的影响，只考虑流场，工质采用常物性参数，工质水的工作温度设为20 °C，FLiBe和 FLiNaK的工作温度设为700 °C，用到的三种工质物性参数如表1所示。

表1 模拟工质Table 1 Working medium of simulation.

正向流动时，流动相对比较简单，计算模型采用标准k-e模型；反向流动时，腔室内部流体呈现涡旋运动，属于复杂剪切流的一种，表现为各向异性和不稳定性。对于旋流问题，可采用的模型有：标准k-e模型、realizablek-e模型、RNGk-e模型[3]、雷诺应力模型[4]以及大涡模型[5]，其中标准k-e模型假定湍流是各向同性的，与涡流二极管反向旋流各向异性不相符，尽管realizablek-e模型、RNGk-e模型相对标准k-e模型进行了有旋改进，但仍不理想，雷诺应力模型直接对各个雷诺应力项进行模化，较前两种有更好的模拟效果，大涡模拟是最符合涡流二极管反向流动，但模拟计算比较耗时间，从模拟结果的比较并结合计算经济性考虑，本文采用雷诺应力模型进行数值模拟计算。

正反向流动均设置为速度进口，恒定出口压力，设置为 0，同时给定水力直径及湍流强度I作为进口湍动条件，反向流动模拟时，由于出口处存在很长一段旋流，模拟采用压力出口边界条件(Pressure outlet)时会在出口处出现回流现象，导致不收敛，所以将出口边界条件设置为 outlet-vent，并通过不断增大阻力损失系数来消除出口处的回流；壁面粗糙度设置为 0，采用标准壁面函数。算法采用压力基准(Pressure-Based)算法，使用多面体网格技术优化四面体网格，压力项的离散采用PRESTO!格式，压力和速度耦合采用SIMPLE算法，动量、湍动能和耗散率各项均采用二阶迎风格式，模拟工质均采用定常流动，并忽略温度场影响，进出口质量流量通量差比低于1×10−5作为收敛准则。

2 计算结果

2.1 涡流二极管正反向流动特性分析

选用工质水做分析，正反向流的进口速度均设为1 m·s−1，图3为涡流二极管内水流的流线图，正向流动时，水流自轴向口流入涡流腔，比较流畅，流阻相对低；反向流动时，水流自切向口流入涡流腔，流体在离心力作用下，在腔室内部产生旋流，并在轴向出口处也存在旋流，进一步增大了流阻。

图3 涡流二极管正反向流线图Fig.3 Flow pathlines of vortex diode.

涡流二极管反向流动时的横向和轴向截面静压分布云图见图4，可以看出，在涡流腔室的外围自由区压降不明显，在腔室中心附近的强制涡区内压降相对就很明显， 涡流二极管反向压降主要集中在腔室中心附近的强旋流区域。

图4 横向和纵向截面静压分布云图Fig.4 Static pressure distribution nephogram of horizontal and vertical section.

2.2 熔盐工质FLiBe和FLiNaK模拟结果

根据 FLiBe和 FliNaK的物性参数并结合PRACS系统工作的工况条件，设定入口速度范围为V=0.5–50 m·s−1，可将流速分为低速流和高速流两种流动状态，通过Fluent软件模拟计算在给定不同的流速条件下，即不同雷诺数下涡流二极管的正反向压降值，并根据求得的压降值获得涡流二极管的性能参数。图5给出了两种熔盐工质 FLiBe和FLiNaK的正反向压降值与雷诺数的曲线图，可以看出，随着雷诺数的不断增大，正反向压降值相应地增大。根据获得的正反向压降值计算涡流二极管的性能参数阻抗比e，结果如图6所示：随着雷诺数的增大，阻抗比增大，当雷诺数达到一定值后，阻抗比基本保持不变；两种熔盐工质的曲线图基本重合，即在相同雷诺数下，FLiBe和FLiNaK的阻抗比非常接近，且能达到的最大值基本相同，因此涡流二极管存在一个临界雷诺数，超过临界雷诺数后，其阻抗比基本保持不变，达到最大值，同时对于结构一定的涡流二极管，其阻抗比与雷诺数有关。

图5 FLiBe (a)、FLiNaK (b)在不同雷诺数下的正反向压降值Fig.5 Forward and reverse pressure values of FLiBe (a),FLiNaK (b) under different Reynolds number.

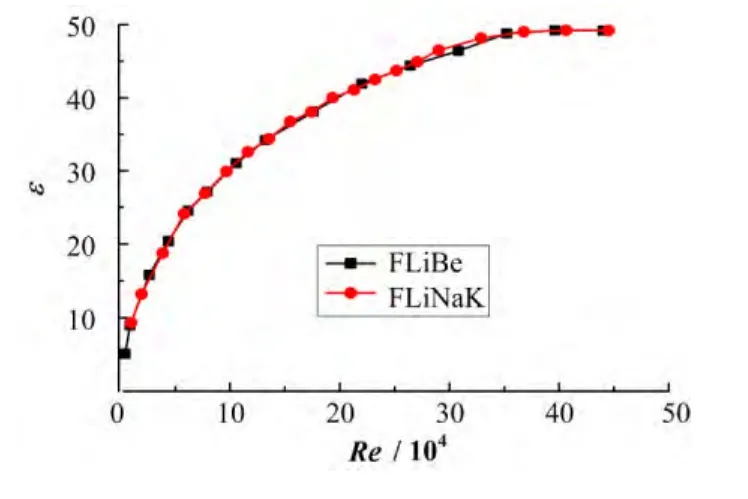
图6 FLiBe和FLiNaK在不同雷诺数下的阻抗比Fig.6 Diodicity of FLiBe and FLiNaK under different Reynolds number.

为了验证涡流二极管性能参数阻抗比e与雷诺数Re相关，增加工质水，模拟结果如图7所示，三种不同工质的曲线图基本重合，即在相同的雷诺数下，涡流二极管性能参数e基本相同。因此对于给定结构的涡流二极管，其阻抗比e与工质的Re有关，而与工质的密度和粘度无关。

图7 三种工质的阻抗比随雷诺数的变化曲线Fig.7 Plot of e vs. Re for three working medium.

2.3 涡流二极管结构优化

为提高涡流二极管性能，对其轴向管和切向管结构进行优化改进，切向管锥角对正反向流场都有影响，随着锥角的增大，正反向流的阻力系数都相应增大，存在一个最佳切向锥角使得涡流二极管的性能比达到最大值，其值在7°左右[6]，轴向管采用渐缩渐扩的结构，优化后的结构如图8所示。

图8 涡流二极管结构优化Fig.8 Structure optimizing model of vortex diode.

为了验证结构优化后，涡流二极管的性能有所提高，采用工质 FLiBe，通过模拟计算，比较优化前后的性能参数。图9(a)显示了结构优化后对正向阻力系数的影响，可以看到，在雷诺数较低的情况下，优化后的正向阻力系数值比优化前大，但随着雷诺数的不断增大，其值相对于优化前的要低一些，造成这一现象的原因是由于优化后的结构相对复杂，在低雷诺数的情况下，其阻力损失相对较大，在雷诺数达到一定值后，轴向管渐缩渐扩的结构起到了对进口流速分布均匀化的作用，正向流的流阻相对于优化前的要低。图9(b)显示了结构优化后对反向阻力系数的影响，优化后的涡流二极管反向阻力系数有了一定程度的提高，这是由于切向管的收缩作用，使得进入腔室的流体切向速度增大，加强了流体从切向管射入腔室的射流效果，更易于在腔室内形成旋流。

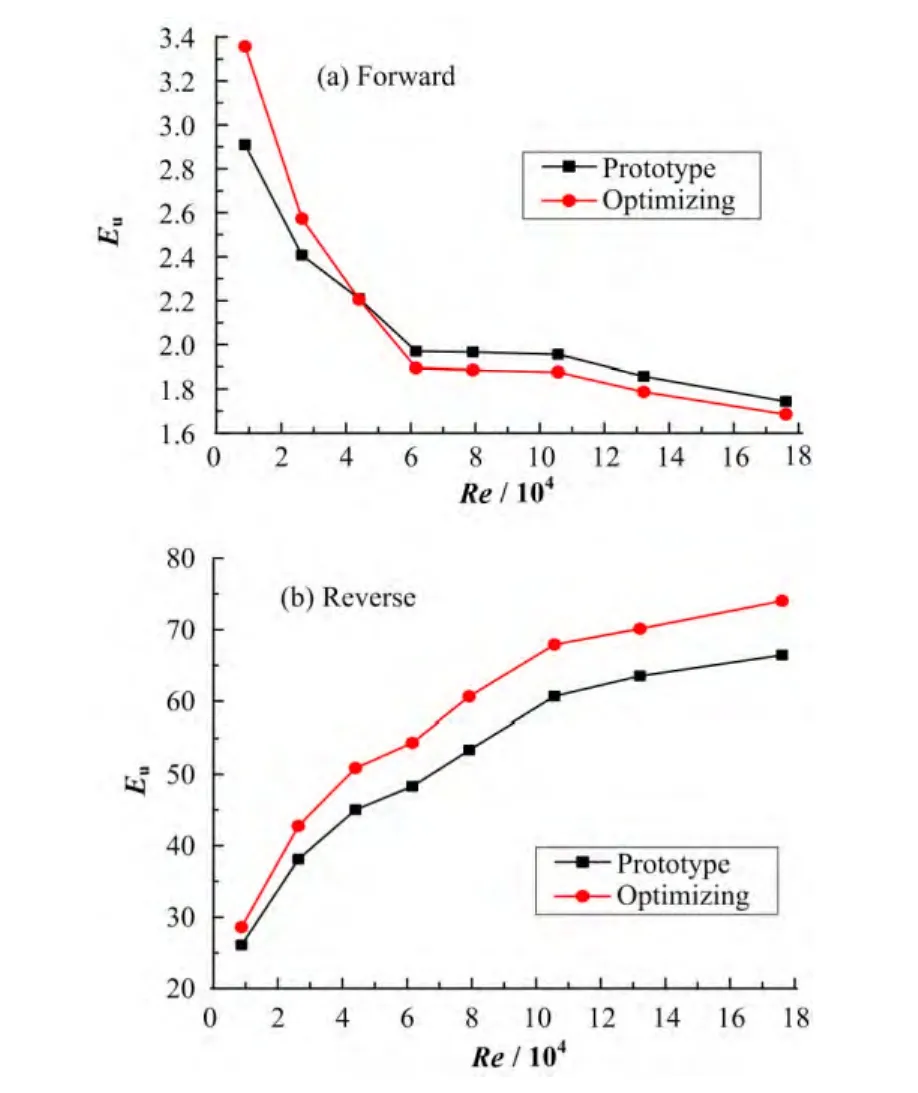
图9 结构优化对正向(a)和反向(b)阻力系数的影响Fig.9 Influence of structure optimization for forward (a) and reverse (b) resistance coefficient.

根据正反向阻力系数的值，得到涡流二极管的阻抗比，结果如图10所示，当雷诺数Re较小时，阻抗比并没有提高，这是由于正向阻力的增大幅度相对于反向阻力的增大幅度相当，但随着雷诺数的进一步增大，涡流腔室内的旋流效果得到加强，反向阻力增加幅度相对于正向的增大幅度有了很大的提高，从而使阻抗比有了一定程度的提高。

图10 结构优化对阻抗比的影响Fig.10 Influence of structure optimization on diodicity.

2.4 实验验证

由于熔盐具有强腐蚀性，不易开展相关实验进行验证，目前开展的涡流二极管实验基本都是水回路，因此从安全和技术成熟角度考虑，本文采用水回路。实验装置如图11所示。

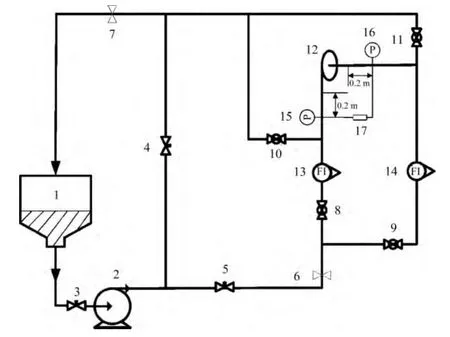
图11 实验装置Fig.11 Experimental setup.

实验采用腔体直径为150mm的结构改进型涡流二极管模型，通过3D打印技术，ABS材料制作而成，由于材料的承受压力有限，将实验流量设定为 2–5 m3·h−1，在此流量变化范围内测定涡流二极管的正反向压降值。

实验过程：先进行反向流动测定，打开阀门8、11，关闭阀门9、10，同时关闭节流阀4，开启其他阀门，以便获得尽可能高的压降，通过调整泵的速度，以增加回路中水的流速。待压力计和压差计数值稳定后，进行采集数据。当反向流动数据采集完后，打开阀门9、10，关闭阀门8、11，将垂直管作为入口进行正向流动测试。节流阀4开启15%的位置，通过泵的调节和节流阀5及球形阀9的进一步微调，尽可能使回路的一系列流量值为反向流动测定时的相关流量值。

在流量范围给定的实验结束后，将实验测得的数据与相应模拟计算结果进行了对比，结果如图12所示。

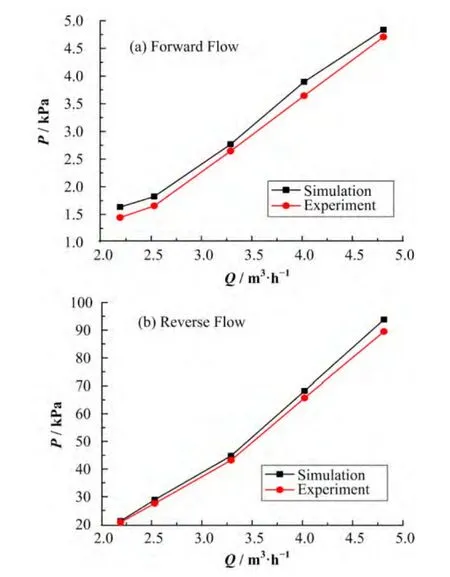
图12 正向流(a)和反向流(b)模拟结果与实验数据的对比Fig.12 Comparison between numerical and experimental results of forward flow (a) and reverse flow (b).

在实验的流量范围内，正反向流动的模拟计算值与实验的数值误差符合模拟计算的精度要求。

3 结语

(1) 通过数值模拟，模拟计算了采用熔盐工质FLiBe和FLiNaK时，涡流二极管在不同雷诺数下的压降值及性能参数。

(2) 对于结构给定的涡流二极管，其性能参数阻抗比e与工质的Re有关，随着Re增大而相应增大，最后达到临界稳定值。

(3) 通过对涡流二极管的轴向管和切向管进行结构优化后，其性能有了一定的提高。

1 Yoder Jr G L, Elkassabgi Y, Cunningham R B,et al.Vortex diode analysis and testing for fluoride salt-cooled high-temperature reactors[R]. ORNL/TM-2011/425, Oak Ridge National Laboratory, TN, USA, 2011

2 郭彦华, 景山, 吴秋林, 等. 涡流二极管泵性能[J]. 高校化工工程学报, 2004, 55(10): 1625–1630 GUO Yanhua, JING Shan, WU Qiulin,et al. Performance of vortex diode pump[J]. Journal of Chemical Industry and Engineering, 2004, 55(10): 1625–1630

3 Speziale C G, Thangam S. Analysis of an RNG based turbulence model for separated flows[J]. International Journal Engineering Science, 1992, 30(2): 1379–1388

4 Launder B E, Reece G J, Rodi W. Progress in the development of a Reynold-stress turbulence closure[J].Journal Engineering, 1994, 72: 953–960

5 Pierce C D, Moin P. Large eddy simulation of a confined coaxial jet with swirl and heat release[C]//AIAA 982892.Albuquerquerque: 29thAIAA Fluid Dynamics Conference,1988: 15–18

6 焦磊, 陈纵楠, 吴淳杰, 等. 切向管结构对涡流二极管性能影响的数值模拟[J]. 工程热物理学报, 2011, 32(3):415–418 JIAO Lei, CHEN Zongnan, WU Chunjie,et al. Numerical simulation of the influence of tangential tube on vortex diode[J]. Journal of Engineering Thermophysics, 2011,32(3): 415–418