多自由度碰磨转子系统非线性动力学特性分析

于 海，陈予恕，曹庆杰

(哈尔滨工业大学航天学院哈尔滨150001)

碰摩是旋转机械的转子与定子之间发生接触而产生的一种故障现象，对旋转机械，转静碰摩是一种常见却又极易引起机械失效的故障现象;随着对旋转机械高转速、高效率的要求，转子与静子的间隙越来越小，导致转子与静子之间的碰摩故障经常发生.季进臣等［1］分析了高速对称刚性当转子两端的轴承同时发生不良润滑时转子圆柱形和圆锥形碰摩运动.Huang［2］用 DK －II扭转振动测试系统测试了转子、定子碰摩系统的扭转振动.刘永强［3］以线性项和立方项之和来表示转轴材料的物理非线性因素.以往针对碰摩研究，系统建模时大多忽略陀螺力矩影响，但是实际转子系统(如航空发动机转子系统)为非对称转子，对于这种结构，考虑陀螺力影响是必要的.

POD(Proper Orthogonal Decomposition)方法最早是由Loeve(1945)和Karhunen(1946)处理信号时提出来的，随着计算工具的发展，正交模态分解技术(POD)已经在各个领域有了广泛的应用［4－5］.近些年来，一些学者将其应用到简单结构的非线性动力系统降维中［6－7］，虽然有一定效果，但降维后系统仍保留了较高的自由度数，无法应用现有的分岔理论对之进行理论分析.

本文的目的是考虑非对称圆盘的陀螺力矩效应，建立含碰摩故障的8个自由度弹性支撑转子系统的动力学模型.引进改进的POD方法成功将具有碰磨故障的8自由度系统降维为等效的两个自由度低维非线性系统.通过数值模拟分析了故障特性:当系统发生碰磨时，其幅频特性有明显变化;为应用现有的理论方法对该系统进行故障机理分析，数值模拟结果显示得到较好降维效果;进而应用C－L方法对其进行分岔分析，讨论了系统参数与系统动态行为之间的关系，得到含碰磨故障转子各种不同分岔模式，准确反映了裂纹转子的动力学特征，为非对称转子的故障机理分析提供理论基础.

1 含碰摩故障系统建模

1.1 碰摩力模型

如图1.

图1 碰摩力模型

采用由线性接触力和库伦摩擦力组合而成的碰摩力模型

其中:r0表示转静间隙是转子的径向位移.

1.2 转子系统模型与建模

如图2、3所示，若圆盘中心位于转轴上任意一点O，当转子以转速Ω自转时，转轴的弯曲变形会产生陀螺力矩H作用到圆盘上.设转轴长为ls，AO的距离为a，BO的距离为b.圆盘运动由平动位移x2，y2和弯曲转角 φx，φy描述，且只考虑转子在轴承处的平动 x1，y1，x3，y3.

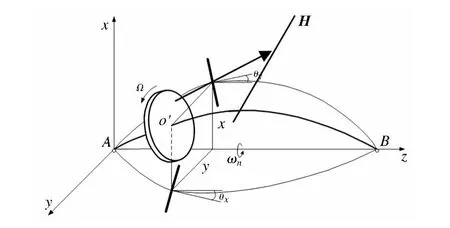
图2 非对称转子模型

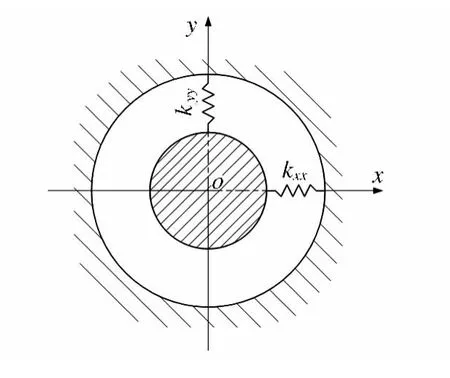
图3 轴承支撑的简化模型

［8－9］的建模方法，利用拉格朗日方法，得到含碰摩故障转子系统模型的动力学方程为:

其中:广义坐标向量为

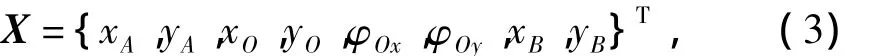
采用无量纲变量 XA=xA/r0，YA=yA/r0，Xo=

则转子系统的无量纲运动微分方程可写为

式中

为对式(4)进行数值求解，取系统的参数的计算数值如下:

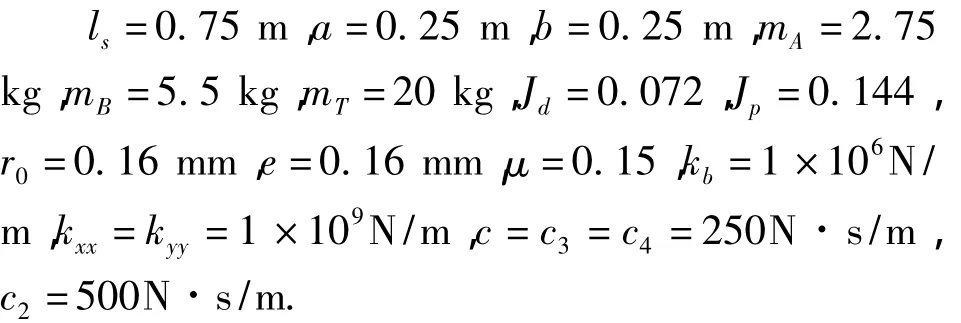
2 故障特征分析

旋转机械的碰摩故障现象是一个较复杂的过程，只有了解转子系统在碰摩过程中的振动特征，才能揭示其运动规律，为大型旋转机械的安全稳定运行提供切实可靠的设计与故障诊断依据.本文模型为非对称转子模型，其陀螺效应影响系统的进动角速度，临界转速等特性，进而影响系统的碰磨故障特性.

图4给出无碰摩故障和含碰摩故障转子系统转盘中心横向位移的幅频图对比，从图4中可以看出，当系统发生碰摩后，会让系统固有频率特性有明显变化，共振峰向右偏移，固有频率略有增加.

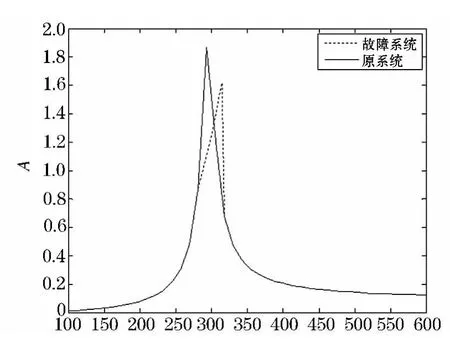
图4 幅频特性对比

3 系统降维

本文引入改进的POD方法对8个自由度系统进行降维:

1)在给定初始条件和转速下，通过实验或者数值仿真，获取各个自由度的过渡过程位移信息，记为z1(t)，z2(t)，… zM(t)，其中每个自由度产生的N个点等时间间隔位移序列，记为zi=(zi(t1)，zi(t2)，…，zi(tN))T，i=1，…，M 这些时间序列可形成矩阵 χ =［z1，z2，…，zM］，χ 为 N ×M 阶.计算自相关矩阵 T=χTχ.求出其特征向量为 φ1，φ2…φM，对应的特征值为λ1＞λ2＞…＞λM.

2)设T=χTχ的前2阶特征向量组成矩阵V对系统坐标Z进行坐标变换，获得一组新坐标P，Z=VP，带入方程(3):

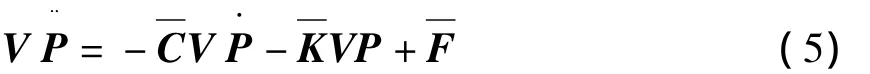
两端左乘(VTV)－1VT:

方程(7)即为降维后2个自由度系统.

4 降维效果比较

式(4)在给定初始条件 zi=0.01(i=1，2，…8)，˙zi=0.01(i=1，2…，8);ω=300(rad/s)的情况下，积分步长选取π/256.

图5为转盘中心横坐标的时间历程图，从图中可以看出:在τ从0～60π之间，系统处于过渡过程;τ在60π之后，系统开始进入周期运动状态.本文τ在0～60π取的位移信息获取变换矩阵对系统降维.

图6给出原系统与降维系统幅频特性的对比.从对比可以看出降维系统基本保持原系统的幅频特性，降维后一阶固有频率与原系统相同，得到较好的降维效果.

图5 在给定初始条件下转盘中心横坐标的时间历程图

图6 幅频特性对比

5 C－L方法

5.1 主共振分岔方程

在以下的讨论中，取 ω21=1+εσ1，ω22=ω21+εσ2.采用平均法，取变换:

其中:A1，A2，θ1，θ2为时间 t的慢变函数.

得到平均方程:

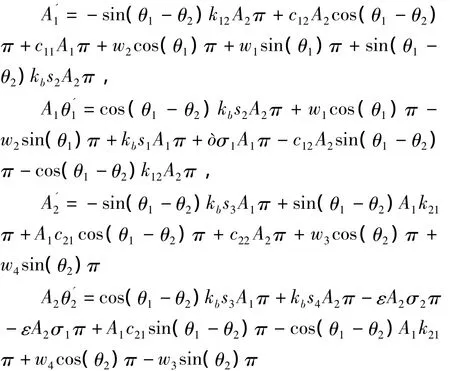
令等号右端等于 0，忽略掉小项，消去 θ1，θ2，可得分岔方程

5.2 分岔分析

吴志强等［10－11］通过引入适当的变换，将约束含参分岔问题转化为新变量的非约束分岔问题，推导出了约束含参分岔问题转迁集的一般形式.秦朝红等［12］将多状态变量分岔理论应用到悬索系统中.李军等［13］将约束分岔理论推广到多状态变量系统中，给出了多状态变量约束系统转迁集的计算方法［14］.本文将应用两状态变量约束分岔理论研究系统的分岔行为.

令 A1=X+1，A2=Y，σ1= λ，根据约束分岔理论［13］考虑转盘处无量纲阻尼和无量纲偏心可求系统的转迁集，如图7，表2.

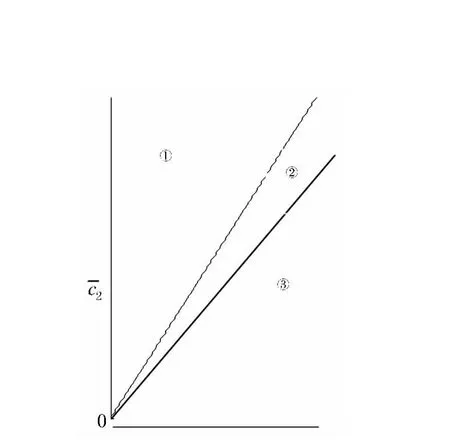
图7 转迁集

6 结语

本文考虑非对称转子的陀螺效应，建立8自由度碰摩转子系统模型，并分析其故障特性;研究结果表明，当系统发生碰摩时，一阶主共振的振幅有明显增加.利用本文作者建议的非线性POD方法，将8个自由度的故障系统降维为保留原系统所有参数影响的2个自由度等效降维系统;对原8个自由度系统数值计算结果与降维系统的结果对比表明，本文对多自由度系统分岔行为的理论分析方法是有效的.此外，本文还利用C－L方法对其进行分岔分析，讨论了系统参数与系统动态行为之间的关系，得到了含碰磨故障转子各种不同分岔模式，准确反映了碰磨转子的动力学特征.该结果对高维转子－轴承系统的碰摩故障诊断及其治理，以及非线性动力学设计有一定指导意义.

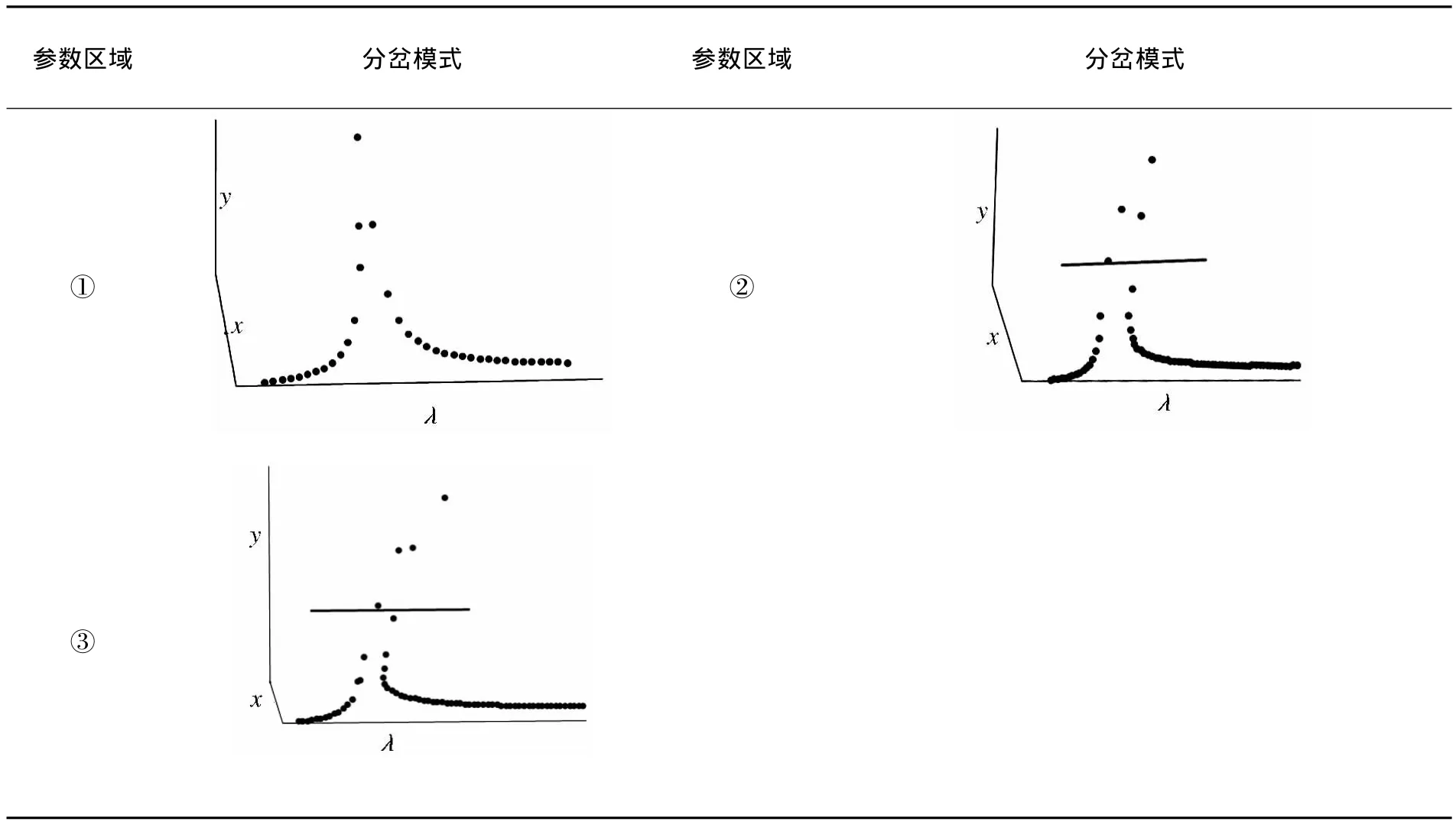
表2 e－c2平面分岔情形

参考文献:

［1］季进臣，虞 烈.高速对称刚性转子碰摩运动的稳定性分析［J］.航空动力学报，1999(1):70－74.

［2］HUANG D G.Experiment on the characteristics of torsional vibration of rotor－ to－ stator rub in turbomachinery［J］.Tribology International，2000，33(2):75 －79.

［3］李永强，刘 杰.非线性刚度不平衡转子径向碰摩动力学研究［J］.应用力学学报，2005(3):45－60.

［4］GLOSMANN P，KREUZER E.Nonlinear system analysis with Karhunen－Loeve transform［J］.Nolinear Dynamics，2005，41(1－3):111－128.

［5］STEINDL A，TROGER H.Methods for dimension reduction and their application in nonlinear dynamics［J］.International Journal of Solids and Structures，2001，38(10－13):2131－2147.

［6］KERSCHEN G，FEENY B F，GOLINVAL JC.On the exploitation of chaos to build reduced － order models［J］.Computer Methods in Applied Mechanics and Engineering，2003，192(13－14):1785－1795.

［7］KAPPAGANTU R，FEENY B F.An“optimal”modal reduction of a system with frictional excitation［J］.Journal of Sound and vibration，1999，224(5):863－877.

［8］钟一鄂.转子动力学［M］.北京:清华大学出版社，1987.

［9］沈 松，郑兆昌，应怀樵.非对称转子－轴承－基础系统的非线性振动［J］.振动与冲击，2004，23(4):31－35.

［10］WU Z Q，CHEN Y S.New Bifurcation Patterns in Elementary Bifurcation Problems with Single－Side Constraint［J］.Applied Mathematics and Mechanics(English Edition)，2001，22(11):1260－1267.

［11］WU Z Q，DING R，Chen Y S.Classification of Parametric Constrained Bifurcation［J］.Applied Mathematics and Mechanics(English Edition)，2010，31(2):135－142.

［12］QIN Z H，CHEN Y S，LI J.Singularity analysis of a two－dimensional elastic cable with 1:1 internal resonance［J］.Applied Mathematics and Mechanics(English Edition)，2010，31(2):143－150.

［13］李 军，陈予恕.两状态变量系统的约束分岔［C］//第十二届全国非线性振动会议，镇江，2009.

［14］YU Hai，CHEN Yu-shu.Application of POD method to reduce dimensions of rotor systern［J］.哈尔滨商业大学学报:自然科学版，2012，28(3):365 －368，378.