构造3 n阶完美幻方的五步法

詹 森，王辉丰

（1.广东技术师范学院 计算机科学系，广东 广州 510665；2.海南师范大学 数学与统计学院，海南 海口 571158）

文[1～10]已讨论了奇数阶幻方和完美幻方的构造方法，其中文[1～5]讨论了奇数阶完美幻方或对称完美幻方.文[1]首先定义了余函数，并运用余函数法构造奇数阶对称完美幻方；文[2]用余函数法构造奇数阶完美幻方.在此基础上，本文将运用[2]的余函数（预备定理）讨论3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方（包括对称完美幻方）的构造方法，文[2]知，以n为周期的余函数

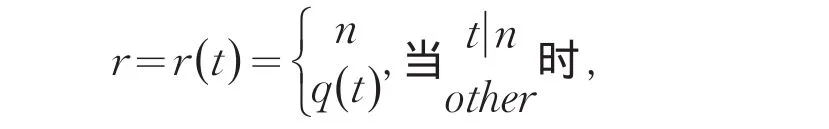
（n、t是自然数，t|n 表示t被n整除，q（t）表示t除以n的余数）具有如下：

预备定理 1）对n=2m+1（m=1，2，…为自然数）.当i=1，2，…，n时，则r（2i）是1～n的自然数，r（4i）也是1～n的自然数.2）对n=2m+1（m为m≠3t+1，t=0，1，2，…的自然数），当i=1，2，…，n时，则r（3i）是1～n的自然数.

1 构造3n阶完美幻方的步骤

第一步 把1～3n（其中n=2m+1，m为自然数）的自然数排成三行n列，使每行n个数字之和都等于(3 n+1)，以(i ,j)记其位于第i行第j列的元素，取

第一行n个数字之和为

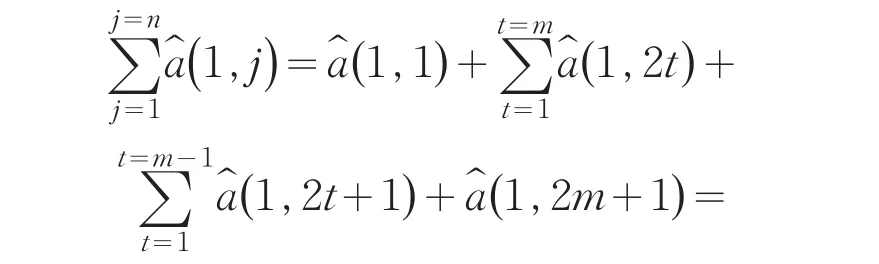
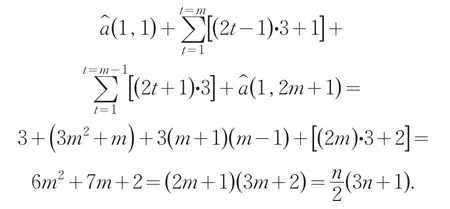
第二行n个数字之和为

第三行n个数字之和为

第二步 用上述 a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn构造3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶基方阵A.

从左到右依次取a1，a2，…，an共三次作为基方阵A的第一行，第一行的元素向左顺移两个位置得第二行，第二行的元素向左顺移两个位置得第三行，依此类推直至得出第n行.

从左到右依次取b1，b2，…，bn共三次作为基方阵A的第n+1行，第n+1行的元素向左顺移两个位置得第n+2行，第n+2行的元素向左顺移两个位置得第n+3行，依此类推直至得出第2n行.

从左到右依次取c1，c2，…，cn共三次作为基方阵A的第2n+1行，第2n+1行的元素向左顺移两个位置得第2n+2行，第2n+2行的元素向左顺移两个位置得第2n+3行，依此类推直至得出第3n行.

以a（i，j）（i=1，2，…，3n，j=1，2，…，3n）记基方阵A位于第i行第j列的元素，则

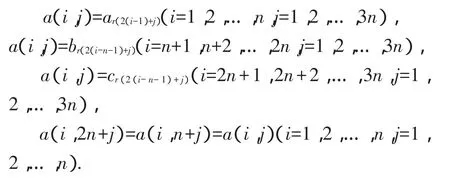
第三步 作基方阵A的转置方阵B.

以b（i，j）（i=1，2，…，3n，j=1，2，…，3n）记转置方阵B位于第i行第j列的元素，则

第四步 作方阵C.

以c（i，j）（i=1，2，…，3n，j=1，2，…，3n）记方阵C位于第i行第j列的元素，取

第五步 构造3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方D.

设方阵D位于第i行第j列的元素为d（i，j）（i=1，2，…，3n，j=1，2，…，3n），则基方阵A与方阵C对应元素相加，即 d（i，j）=a（i，j）+c（i，j）=a（i，j）+（b（i，j）-1）·3n（i=1，2，…，3n，j=1，2，…，3n）.所得方阵D就是所要构造的一个3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶完美幻方（见以下定理证明）.上述步骤称为五步法.

2 定理及证明

定理 由上述五步法所得3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶方阵D是一个完美幻方.

证明 分五步证明如下：1）先证基方阵A是一个3n阶非正规完美幻方.由基方阵A的构造知，基方阵A第1～n行，各行3n个元素之和都等于

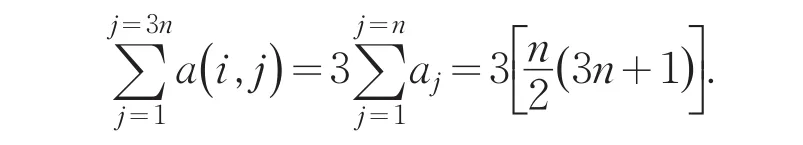
第n+1～2n行，各行3n个元素之和都等于

第2n+1～3n行，各行3n个元素之和都等于

每例患者的辐射剂量参数包括容积CT剂量指数(volume CT dose index，CTDIvol)、剂量长度乘积(dose length product，DLP)，在肝脏灌注扫描完成后由机器自动生成。计算有效辐射剂量(effective radiation dose，ED)，ED=DLP×k，其中k为换算系数，上腹部扫描时k=0.015 mSv·mGy-1·cm-1[14]。

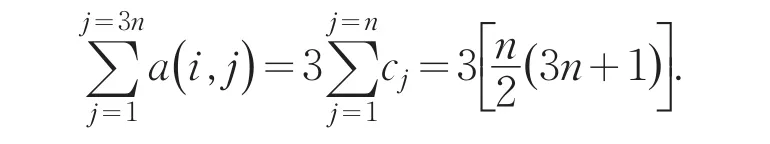
即基方阵A各行3n个元素之和都等于

考察基方阵A各行3n个元素之和

在求和过程中，j-2是固定的，由的预备定理知，

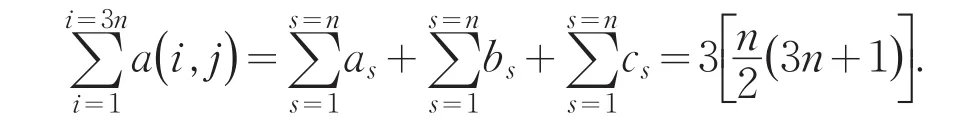
过a（h，1）（h=1，2，…，n）从左上角至右下角的对角线以及与其同方向的泛对角线上的元素a（i，j）而言，有r（i-j）=h-1（h=1，2，…，n），所以，其上各元素之和为

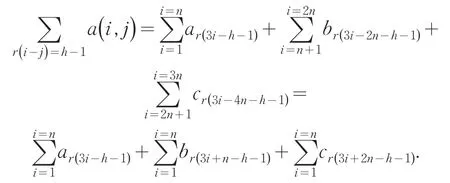
在求和过程中，-h-1，n-h-1和2n-h-1都是固定的，由预备定理得

过b（h，n）（h=1，2，…，n）从左下角至右上角的对角线以及与其同方向的泛对角线上的元素b（i，j）而言，有r（i+j）=h（h=1，2，…，n），所以，其上各元素之和为

在求和过程中，-2+h，-n-2+h和-2n-2+h和都是固定的，由预备定理得

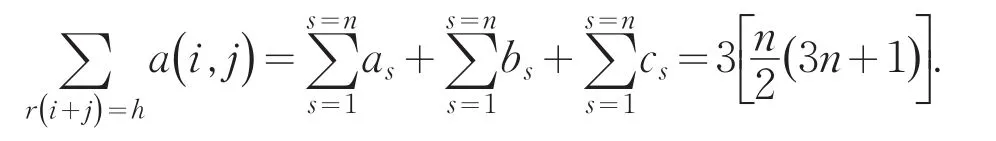
3）由于方阵C位于第i行第j列的元素c（i，j）=（b（i，j）-1）·3n（i=1，2，…，3n，j=1，2，…，3n），所以方阵C是一个非正规完美幻方，其幻方常数为

4）由于方阵D是由基方阵A与方阵C对应元素相加所得，方阵D是一个完美幻方，其幻方常数为

5）最后我们还需证明方阵D是一个正规的完美幻方.

考察基方阵D的元素，

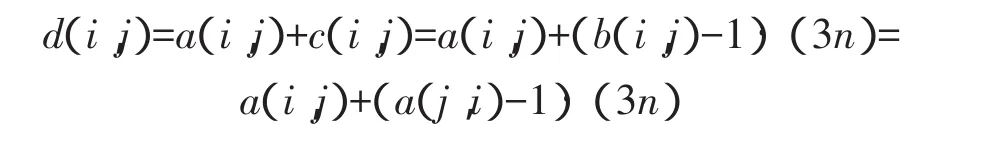
由预备定理，对n=2m+1（m为m≠3t+1，t=0，1，2，…的自然数），当i=1，2，…，n时，则r（3i）是1～n的自然数.所以r（-3i）=r（n-3i）是1～n的自然数.

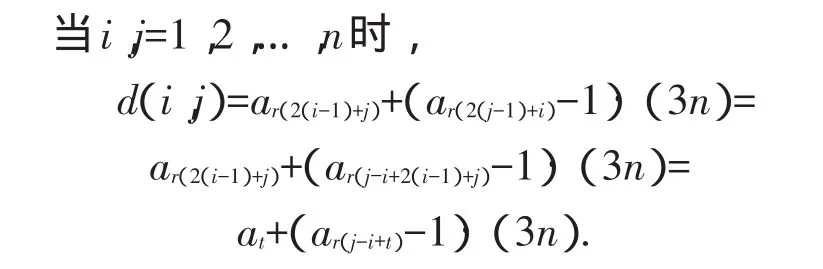
对于每一个 t=1，2，…，n，r（2（t+1）-3i）取遍1～n的自然数，即at加遍（a1-1）（3n）～（an-1）（3n），当i=1，2，…，n，j=n+1，n+2，…，2n时，

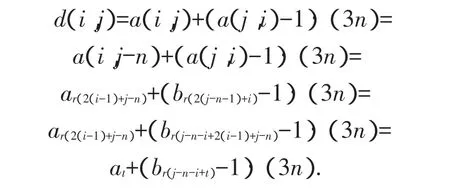
对于每一个 t=1，2，…，n，r（2（t+1）-3i）取遍1～n的自然数，即at加遍（b1-1）（3n）～（bn-1）（3n）.当i=1，2，…，n，j=2n+1，2n+2，…，3n时，

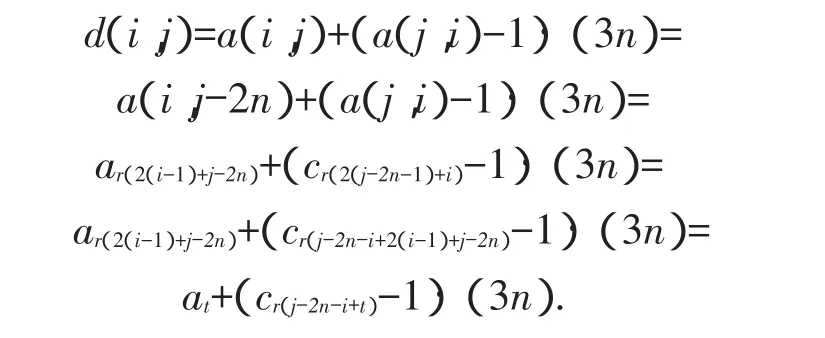
对于每一个 t=1，2，…，n，r（2（t+1）-3i）取遍1～n的自然数，即at加遍（c1-1）（3n）～（cn-1）（3n），因为a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn取遍1～3n的自然数，所以at（1，2，…，n）加遍0，1·（3n），2·（3n），…，（3n-1）·（3n）.

同理可证bt（t=1，2，…，n）加遍0，1·（3n），2·（3n），…，（3n-1）·（3n）；ct（t=1，2，…，n）加遍0，1·（3n），2·（3n），…，（3n-1）·（3n）.

完美幻方D是由1～3n，3n+1～2·（3n），2·（3n）+1～3·（3n），…，（3n-1）·（3n）+1～（3n）·（3n）的自然数所组成，即由1～（3n）2的自然数所组成，即方阵D是一个3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶正规的完美幻方.证毕.

由于a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn都各有n!种选法，故五步法可得到（n!）3个不同的3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶正规的完美幻方.

3 构造3n阶对称完美幻方的方法

在构造3n阶完美幻方的步骤中，只需选取a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn使方阵A为一个对称方阵，其他步骤不变就可构造出3n阶对称完美幻方，这样实际上就是以上定理的推论（见以下推论）.

推论 当a1，a2，…，an；b1，b2，…，bn；c1，c2，…，cn的选取使方阵A为一个对称方阵时，五步法得到的是一个3n（n=2m+1，m为m≠3t+1，t=0，1，2，…的自然数）阶正规的对称完美幻方.

例 构造一个15阶对称完美幻方.

根据五步法第一步得

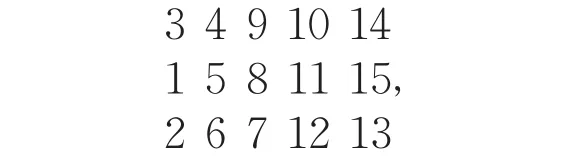
取4，9，10，14，3依次为a1，a2，a3，a4，a5.取5，8，11，15，1依次为b1，b2，b3，b4，b5.取6，7，12，13，2依次为c1，c2，c3，c4，c5.

以上得到了构造3n阶完美幻方或对称完美幻方的结果，对于解决文[11]（构造n=3（2m+1）阶对称完美幻方一直是一个未解决的问题）指出的难题起着很大的作用.我们将在“构造奇数3（2m+1）阶完美幻方的方法”一文中彻底解决这个难题.

由第二步得15阶方阵A（见图1）.

图1 15阶方阵AFig.1 15-order matrix square A

图2 15阶对称完美幻方DFig.2 15-order symnetry pertect magic squave D

由第三步得A的转成方阵B（略）；由第四步得方阵C（略）；由第五步得15阶对称完美幻方D（见图2）.

[1]詹森,王辉丰.奇数阶对称完美幻方的构造方法[J].海南师范大学学报：自然科学版,2009,22(4)：396-402.

[2]詹森,王辉丰.构造奇数阶幻方,完美幻方和对称完美幻方的新方法[J].海南师范大学学报：自然科学版,2011,24(3)：265-269.

[3]王辉丰.构造奇数阶完美幻方和对称完美幻方的两步法[J].海南师范大学学报：自然科学版,2012,25(1)：28-31.

[4]詹森,王辉丰.奇数阶对称完美幻方的构造方法[J].海南师范大学学报：自然科学版,2009,22(4)：396-402.

[5]詹森.关于构造k2阶完美幻方的方法[J].海南师范大学学报：自然科学版,2012,25(2)：147-157.

[6]王辉丰,詹森.关于构造三类奇数阶幻方的新方法[J].海南师范大学学报：自然科学版,2010,23(1)：12-15.

[7]詹森,王辉丰.构造镶边幻方代码法[J].海南师范大学学报：自然科学版,2010,23(2)：152-157.

[8]詹森,王辉丰.关于构造高阶幻方的新方法[J].海南师范大学学报：自然科学版,2009,22(3)：250-254.

[9]詹森,王辉丰.构造奇数阶对称幻方及奇偶数分开对称幻方的新方法[J].海南师范大学学报：自然科学版,2011,24(4)：395-399.

[10]詹森,王辉丰,黄澜.构造奇偶数阶幻方的四步法[J].海南师范大学学报：自然科学版,2013,26(2)：145-151.