一类广义Liénard方程周期解的不存在性

胡宇峰

（岳阳县第一中学，湖南 岳阳 414100）

0 引 言

Liénard方程在平面微分系统的研究中有着非常重要的地位，对Liénard方程极限环的研究是平面微分系统定性理论研究的重要课题。

对于广义Liénard方程

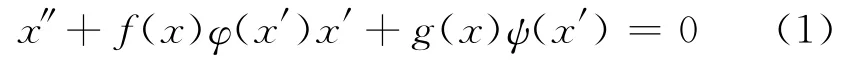
的特殊情形：

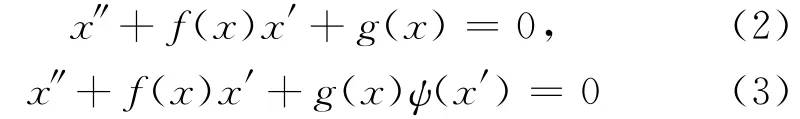
已有许多的研究，其中对其周期解的不存在性涌现出大量优秀的结果［1－5］。

本文运用极限集理论与Poincaré切性曲线法，对较一般的广义Liénard方程（1）给出了其周期解不存在的两个充分条件，并在文章的最后举例说明了所得结果的应用。

下面先介绍一个定义和引理。

轨道l的所有ω极限点构成的集合，称之为它的ω极限集合，记为Ωl；所有α极限点构成的集合，称之为α极限集合，记为Al。

引理2［6］若轨道l有界，并且 Ωl（Al）最多含有有限个奇点；则以下三个结论之一必定成立：

Ωl（Al）仅由唯一一个奇点P0构成，此时当t→＋∞（t→－∞）时，轨道l趋于奇点P0；

Ωl（Al）由一条闭轨线L构成，此时当t→＋∞（t→－∞）时，轨道l盘旋逼近于L；

Ωl（Al）是由有限个奇点和一些极限轨道构成的，此时当t→＋∞（t→－∞）时，这些极限轨道都各自分别趋向于这些奇点当中之一。

现考察广义Liénard方程（1）的等价系统：

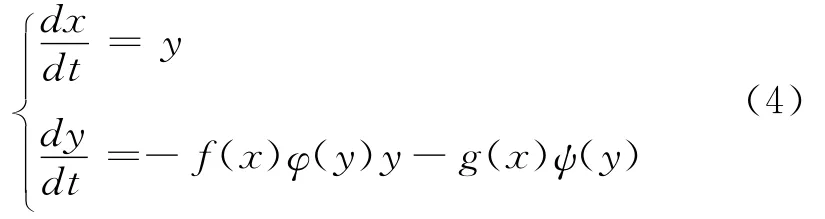
1 主要结果及证明

定理2 假设系统（4）满足以下条件：

（H1）f（x）φ（y）与g（x）ψ（y）关于x，y满足局部Lipschitz条件；

（H2）当x≠0时，xg（x）＞0；存在β，γ＞0，使得对任意y∈R有0＜φ（y）≤β，0＜ψ（y）≤γ；

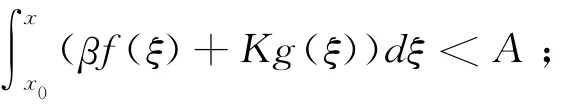
则系统（4）不存在非零周期解。

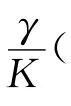
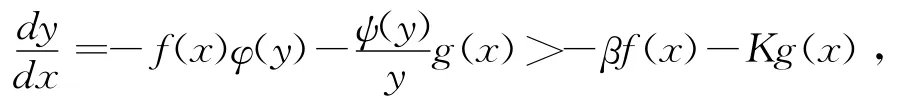
从而

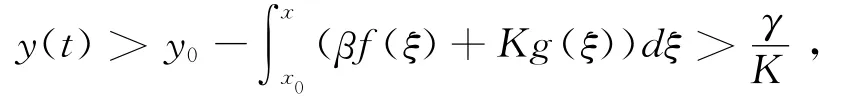
现取V（x，y）＝G（x）＋Ψ（y），由条件（H2）及（H4）知当0＜C＜M时V（x，y）＝C表示一系列含有原点的简单闭曲线，且对系统（4）有

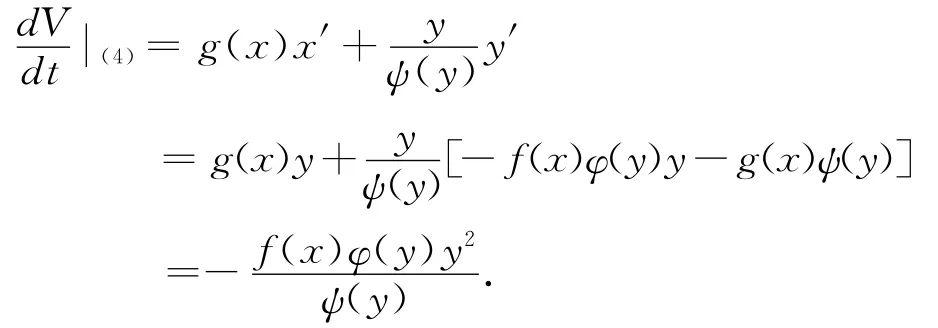
由条件（H4）知，当0＜C1＜M，闭曲线V（x，y）＝C1的点（x，y）满足：x∈ （－ x1，x1），而由条件（H2）及（H4）得：当x∈ （－ x1，0）∪ （0，x1）时，有

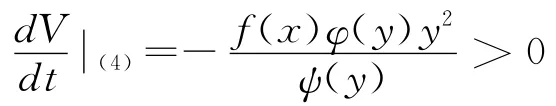
用B表示平面有界区域G（x）＋Ψ（y）＜M，而

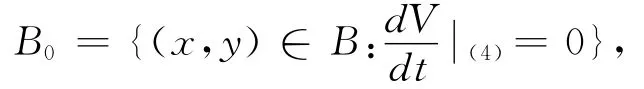
则B0不包含系统（4）的整条非零轨线，这样根据Poincaré切性曲线法知，在区域B中不包含系统（4）的闭轨线以及不存在只含一个奇点的闭轨线。

这时再结合Poincaré切性曲线法及引理知，负半轨Γ（D，R－）必趋于系统（4）的唯一奇点原点。这就证明了系统（4）存在一条轨线，它的一边趋于原点，而另一边则趋于无穷。因而若系统（4）有闭轨线，则得出此闭轨线必含唯一奇点，既而它与轨线Γ（D，R）相交，这时就不符合解的唯一性，因此系统（4）不存在周期解。

定理3 假设系统（4）满足以下条件：

（H5）f（x）φ（y）与g（x）ψ（y）关于x，y满足局部Lipschitz条件；

（H6）当x≠0时，xg（x）＞0；对任意y∈R，φ（y）＞0，ψ（y）＞0；

（H7）存在常数d＞0，当x≤－d且固定时，f（x）φ（y）y＋g（x）ψ（y）是y的单调递增函数；

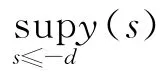
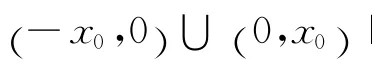
（H9）Ψ（（±∞）＞m ，

则系统（4）不存在非零周期解。

证明 对方程

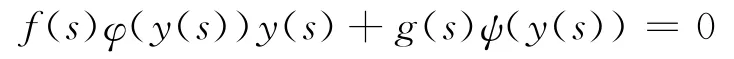
的解y（s），定义p（x）如下：

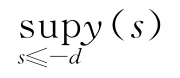
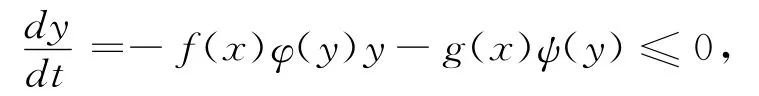
2 例 子

在本文中给出了广义Liénard方程（1）周期解不存在性的两个充分条件，及较为详细的证明过程。很明显地可以发现，在定理2和定理3中，系统（4）在φ（y）≡ψ（y）≡1时，方程（1）就是方程（2），方程（3）。

下面给出两个例子：

例1 考虑下面系统周期解的存在性。

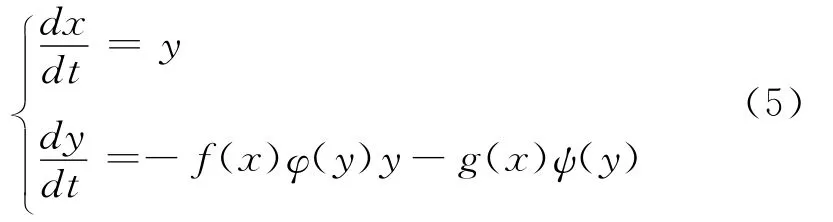
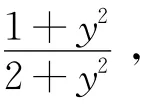
解 很容易检验出系统（5）满足定理2中的条件（H1）－（H4），其中β＝1，γ＝2，这样根据定理2可知系统（5）不存在非零周期解。

例2 考虑系统

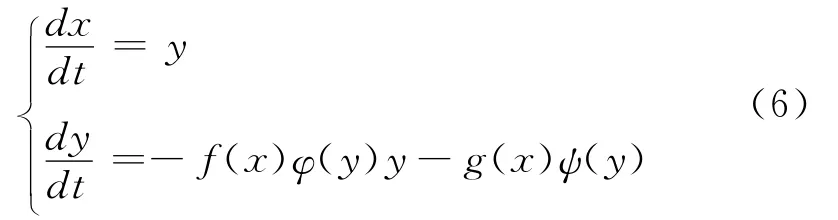
（其中f（x）＝2000－x3，φ（y）＝π＋arctany，g（x）＝x，ψ（y）＝e－y3）周期解的存在性。

解 通过验证定理3中的条件，由定理3可知系统（6）不存在非零周期解。

致谢：作者感谢湖南工业大学赵育林教授的指导！

［1］叶彦谦.极限环论［M］.上海：上海科技出版社，1984.

［2］Villari G.On the qualitative behaviour of solutions of Liénard equation［J］.Journal of Differential Equations，1987，67（2）：269－277.

［3］Sugie J.Some criteria the existence of limit cycles for a planar system of Liénard type［J］.Nolinear Analysis，1993，21（11）：801－814.

［4］严平，蒋继发.广义Liénard方程非平凡周期解的存在性［J］.应用数学，2000，13（1）：31－34.

［5］Timoteo Carletti，Gabriele Villari.A note on existence and uniquenessof limit cycles for Lienard systems［J］.Journal of Mathematics Analysis and Application，2005，307：763－773.

［6］尤秉礼.常微分方程补充教程［M］.北京：人民教育出版社，1981：268.