迭代收缩SL0压缩感知恢复算法

刘婉军， 王宏志， 王贤龙

（长春工业大学 计算机科学与工程学院，吉林 长春 130012）

0 引 言

压缩感知（Compressed Sensing，CS）信号处理理论提出以来，压缩感知信号恢复算法的研究一直是压缩感知理论研究重点。在压缩感知理论框架下，信号经过稀疏表示，在适当的测量矩阵下采样，仍然能够从低维采样信号中以很高的精度恢复出原始信号［1－2］。从数学上来说，CS理论指出如果信号是可稀疏表示的，测量矩阵满足RIP［2］条件，就可以高概率从欠定采样信号中恢复出原信号。目前，国内外很多学者在研究压缩感知信号恢复算法，并且取得了一些成果［3－6］。压缩感知的重构算法主要分为贪婪算法［7］和凸优化算法［1］。SL0算法［8］是结合贪婪算法和凸优化算法的一种欠定问题求解算法。由于SL0用一个连续函数的极限表示L0范数，所以求解并不像凸优化算法求解近似线性最优化问题，而是一个非线性最小化问题。SL0算法在算法恢复精度优于凸优化算法中的BP算法［9－10］，同时速度是优于贪婪算法［9－10］。因为SL0算法在压缩感知信号处理的高效性，SL0算法被许多学者研究，并相应提出了许多改进算法［11－13］。文中在原有SL0算法的基础上引入迭代收缩，提出迭代收缩压缩感知SL0PL算法，加快每次最小值搜索速度，减少总的迭代次数，从而使得信号在恢复精度不变的情况下，减少信号恢复时间。

1 SL0压缩感知算法介绍

压缩感知理整体框架［1］如图1所示。

图1 压缩感知信号处理框架

原始信号s∈Rn可以用某个正交基Ψ 稀疏表示为Θ∈Rn，将稀疏信号Θ经过测量矩阵Φ∈Rm×n进行采样，得到采样信号y∈Rm。在信号接收端，通过求解式（1）恢复原信号

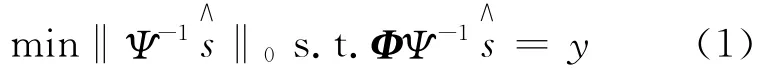
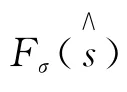
其中

满足这种性质的函数有很多。SL0压缩感知算法中采用高斯函数

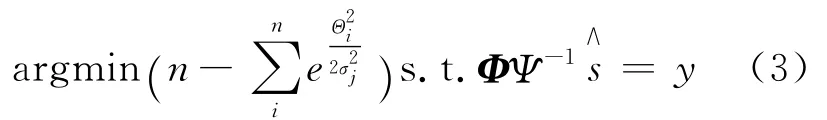
使用最速下降法循环迭代式（3），σj＝∂σj－1，∂是下降比例。迭代直到两次计算误差小于阈误差TOL或者σj＜σmin迭代结束，求得恢复信号。

2 迭代阈值收缩SL0算法

SL0算法是压缩感知信号恢复算法中一种较为有效的恢复算法。无论在理论分析或者实际应用中，SL0算法的有效性都得到了证明［9－10］。其恢复速度是BP算法的2～3倍［9－10］。文中将SL0算法应用于图像分块压缩感知的时候发现，在SL0算法中引入迭代收缩可以减小SL0算法迭代次数，加快每次迭代局部最优解寻找过程，从而减少信号恢复时间。

阈值收缩算法广泛应用于迭代最小化问题求解当中。对于最小化问题

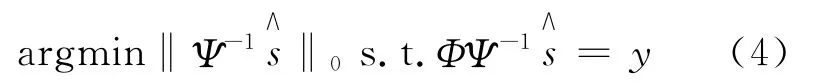
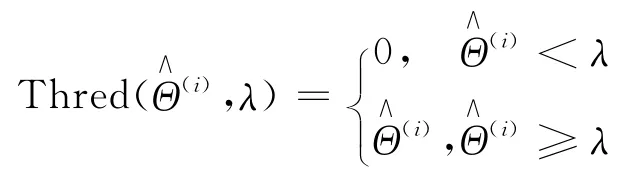
在前文分析的SL0算法中，SL0算法也是利用不断的迭代使用最速下降法［6］去寻找最优解。这个思想和阈值收缩是一致的，因此，在SL0每次的迭代过程中加入阈值收缩步骤。同时，SL0算法每次迭代中σ是动态改变的，如果使用固定的收缩阈值，就会导致在不同的σ的情况下，阈值收缩对恢复信号影响不一致，甚至会降低信号恢复质量。因此，定义阈值函数：

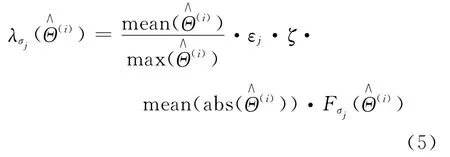
n——原始信号长度。

在每次迭代中，先用最速下降法求得本次迭代最优解，然后再进行一次阈值收缩。整个算法步骤如下：

1）利用最小二乘法求得一个近似解

2）最速下降法求解局部最小值

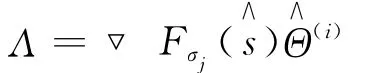
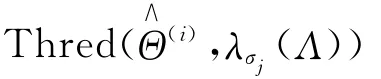
4）步骤2），3）循环L次，计算与第i－1次恢复结果的残差e，如果误差e小于阈值TOL或者迭代次数超过最大迭代次数Imax，结束。否则进入步骤5）。

5）阈值收缩系数εj＋1＝εjη，其中η是下降比例，σj＋1＝∂σj进入步骤2）。

3 实验结果

为了验证迭代收缩算法的信号恢复效果以及恢复时间确实如上述理论分析所说，对一维随机信号进行实验。

选取信号长度为n＝1 000的随机信号，采样率ration从0.2～0.9，采样矩阵采用高斯随机矩阵，每个采样率重复实验10次，对重复实验的结果取平均值作为该采样率的实验结果。实验中，最速下降法最大迭代次数L＝3，迭代误差阈值TOL＝0.000 1，收缩阈值稀疏ε下降比例η＝0.86。整个迭代，最大迭代次数Imax＝100。记录每个采样率信号恢复时间以及恢复信号信噪比PSN。得出的实验数据如图2所示。

图2 SL0算法与迭代收缩SL0算法恢复比较

SL0和迭代收缩SL0算法迭代次数比较见表1。

表1 SL0和迭代收缩SL0算法迭代次数比较

从图2和表1可以看出，用迭代收缩SL0信号恢复算法，在相同采样率条件下，需要的迭代次数比SL0平均减小3～6次，迭代次数减少不但使得信号恢复时间减少，同时避免对最优解过操作，使得信号恢复质量降低。迭代收缩SL0的恢复时间相比于SL0恢复算法有一定的提升，特别是在采样率比较高，采样信号数据量大，恢复时间有比较明显的减少。而且恢复信号的信噪比在采样率为0.9的时候也达到了将近3dB的提升。

4 结 语

通过上述理论以及实验分析，可以证明迭代收缩SL0算法是一种有效的压缩感知信号恢复算法。无论在信号恢复时间以及恢复信号的质量上都优于SL0算法。实验中发现，SL0算法以及改进的SL0算法信号恢复时间与采样率的关系并不是线性关系，这表明SL0算法参数选择在当前采样率是不合适的，导致恢复算法不稳定。因此，未来的研究重点是引入自适应参数，使得恢复算法保持稳定性。

［1］Donoho D L.Compressed sensing［J］.Information Theory，IEEE Transactionson，2006，52（4）：1289－1306.

［2］CandèS E J，Romberg J，Tao T.Robust uncertainty principles：Exact signal reconstruction from highly incomplete frequency information［J］.Information Theory，IEEE Transactionson，2006，52（2）：489－509.

［3］焦李成，杨淑媛，刘芳，等.压缩感知回顾与展望［J］.电子学报，2011，39（7）：1651－1662.

［4］戴琼海，付长军，季向阳.压缩感知研究［J］.计算机学报，2011，34（3）：425－434.

［5］石光明，刘丹华，高大化，等.压缩感知理论及其研究进展［J］.电子学报，2009，37：1070－1081.

［6］CandèE J S，Wakin M B.An introduction to compressive sampling［J］.IEEE Signal Processing Magazine，2008，25（2）：21－30，1070－1081.

［7］Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit［J］.Information Theory，IEEE Transactionson，2007，53（12）：4655－4666.

［8］Mohimani G H，Babaie Zadeh M，Jutten C.Fast Sparse Representation based on Smoothed？0 Norm［C］／／Independent Component Analysis and Signal Separation.Springer Berlin Heidelberg，2007：389－396.

［9］Mohimani H，Babaie Zadeh M，Gorodnitsky I，et al.Sparse Recovery using Smoothed ＄／ell＾0＄（SL0）：Convergence Analysis［C］.arXiv Preprint arXiv：2010，1001：5073.

［10］Hyder M，Mahata K.An approximate L0norm minimization algorithm for compressed sensing［C］／／Acoustics，Speech and Signal Processing，2009.ICASSP 2009.IEEE International Conferenceon.IEEE，2009：3365－3368.

［11］王军华，黄知涛，周一宇，等.基于近似L0范数的稳健稀疏重构算法［J］.电子学报，2012，40（6）：1185－1189.

［12］Cui Z H，Zhang Lu W.An Improved Smoothed l0－norm Algorithm Based on Multiparameter Approximation Function，in 12th IEEE International Conference on Communication Technology （ICCT）［C］／／China：Nanjing，2010：11－14，942－945.

［13］Mohimani H，Babaie Zadeh M，Jutten C.A fast approach for overcomplete sparse decomposition based on smoothednorm［J］.Signal Processing，IEEE Transactionson，2009，57（1）：289－301.