位移法在静定结构的应用

叶 腾

（漳州职业技术学院，福建 漳州 363000）

0 引 言

综观结构力学教材对位移法的表述是：位移法是解决超静定结构的一种基本方法，利用位移法既可以计算超静定结构的内力，也可以计算静定结构的内力。而对如何将位移法运用于静定结构的分析，则语焉不详，没有实际的例子［1－8］。文中就几个算例尝试说明位移法是如何在静定结构的位移和内力计算中的应用。

1 静定结构的位移计算

谈到静定结构的位移计算，一般第一反应就是采用虚功原理之单位荷载法，或用积分、或用图乘法加以计算确定。

算例1：若欲求转角θA，作为位移状态如图1所示。

通常是在A处施加一个单位力偶，建立虚拟力状态，如图2所示。

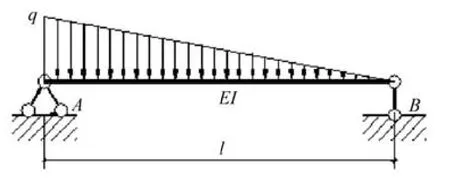
图1 位移状态

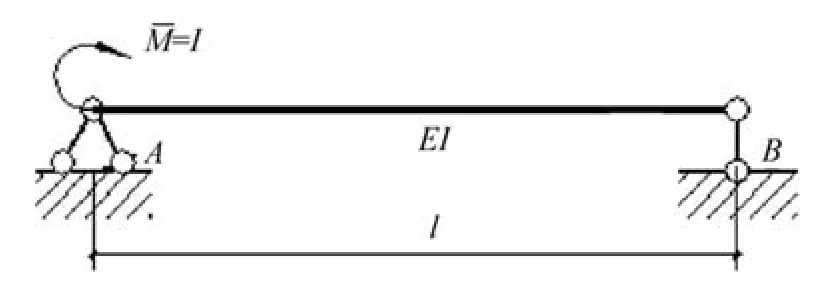
图2 虚拟力状态

设B为x轴原点指向A。

分别求出两种状态的支座反力，进而建立两种状态的弯矩方程如下：

则

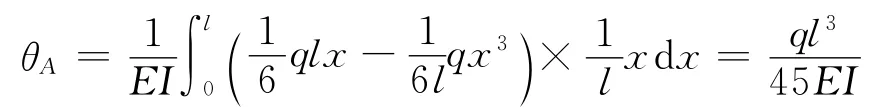
该方法需要建立虚拟力状态和位移状态两种状态的弯矩方程，若在复杂荷载情况下，容易出错，并且可能需要分段积分，计算过程繁杂。

算例2：求图3（a）C的竖直位移Δcv。

通常分别作出M和M 图，然后采用图乘法可以求得：

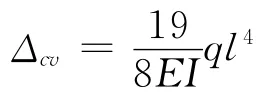
由于AC和CB段的弯矩图均为非完整抛物线，所以在计算过程中经常容易出现错误。

位移法的基本出发点是先考虑变形协调条件，然后根据平衡条件确定变形的唯一性。当我们熟悉了单跨超静定梁的形常数和载常数后，特别是单跨静定梁，可以通过对静定结构适当的改造，即在欲求位移的方向上添加相应的约束，然后利用位移法的杆端位移方程，并考虑改造后的结构与原结构在添加约束处的静力平衡关系，可以很方便地进行位移计算。

图3 算例2结构图

如算例1，设在A处添加一个约束，并令A产生转角θA，如图4所示。

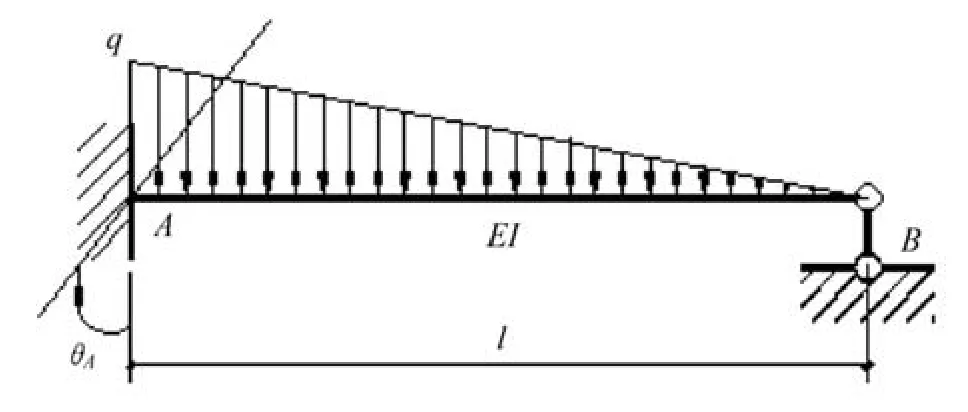
图4 算例1添加约束后的转换结构

利用单跨超静定梁的形常数和载常数则有：

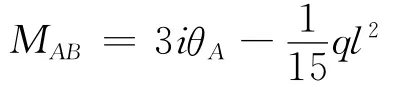
原结构A是铰结点，所以有：

求得：

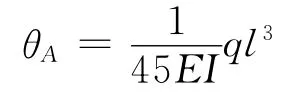
结果一致。

如算例2，在C处添加一个链杆支座，如图5所示。

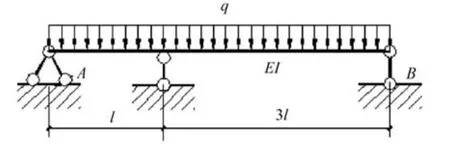
图5 算例2添加约束后的转换结构

并令向下产生位移Δ。

设

则

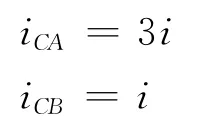
杆端位移方程：

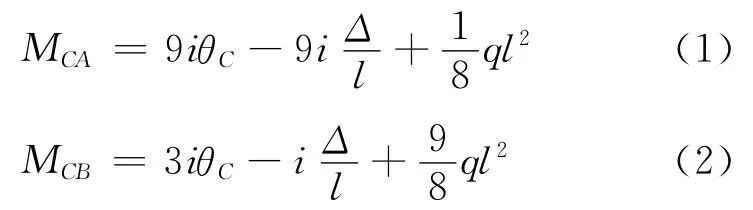
实际结构如图3（b）有

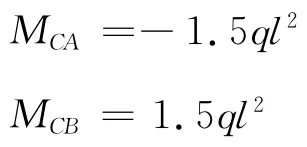
代入式（1）和式（2）中即可求出：

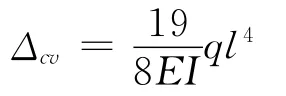
结论一致。

2 静定半刚架的弯矩及侧移计算

静定开敞的半刚架存在的固有特性，使得采用位移法可以很方便绘出弯矩图，并快速求得侧向位移。

算例3：作图6结构的弯矩图，并求ΔCH。

位移法解：

AC，CB杆端位移方程为：

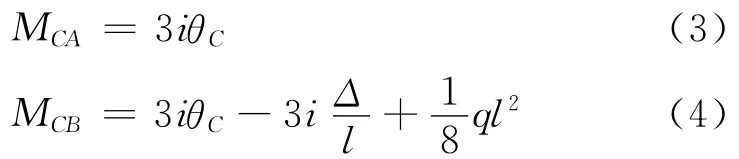
图6（b）有

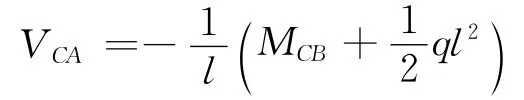
利用截面平衡

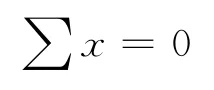
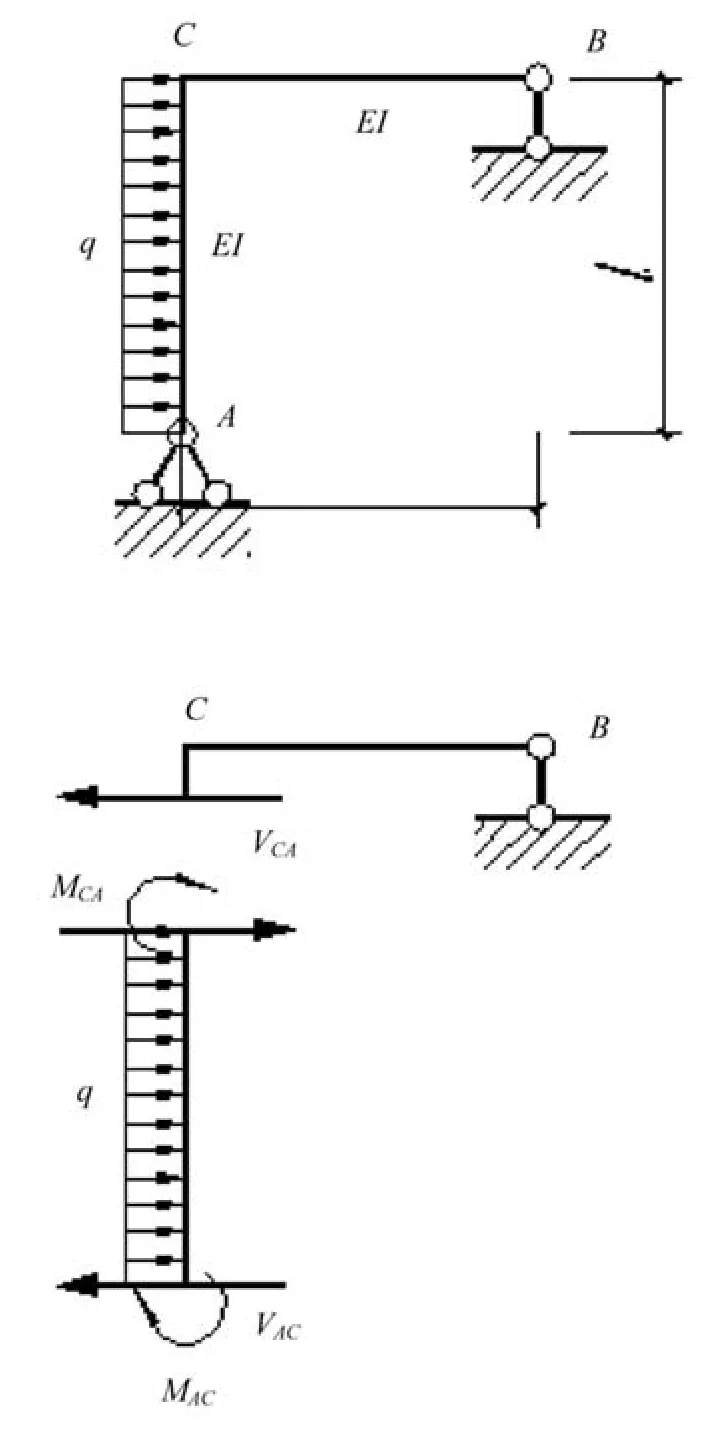
图6 算例3结构图

有：

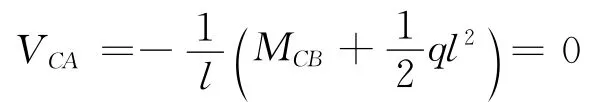
则

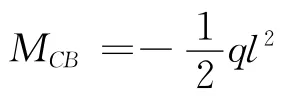
利用结点C力矩平衡

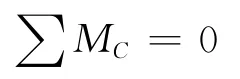
有：

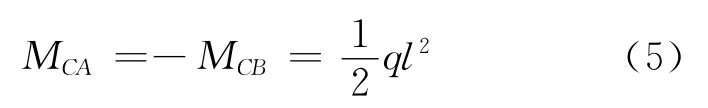
据此，即可运用叠加原理作出该结构的弯矩图。

同时将式（5）的结果代入式（3）和式（4）即可求得：

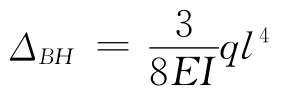
3 结 语

位移法的基本出发点是先考虑变形协调条件，然后根据平衡条件确定变形的唯一性。当熟悉了单跨超静定梁的形常数和载常数后，可以融会贯通，通过对静定结构的适当改造，是可以采用位移法很方便地进行位移计算。同时，对于某些特定的结构可以不必求解支座反力，即能作出弯矩图。

［1］包世华.结构力学（下册）［M］.武汉：武汉工业出版社，2000.

［2］杨天祥.结构力学［M］.北京：高等教育出版社，1997.

［3］孙晔清.试论支座的线位移对结点位移数的影响［J］.力学与实践，2005，27：123－126.

［4］徐鹏辉.位移法计算特征与算例分析［J］.知识经济，2013（5）：38－45.

［5］胡兴国，吴莹.结构力学［M］.2版.武汉：武汉理工大学出版社，2002.

［6］安松柏.建筑力学［M］.北京：中国环境科学出版社，2005.

［7］李永光.建筑力学与结构［M］.北京：机械工业出版社，2006.

［8］陈永龙.建筑力学（多学时）（上册）［M］.北京：高等教育出版社，2003.