基于电磁场模型的轨道电路钢轨阻抗研究

朱 冰，刘中田，周 果

(北京交通大学 电子信息工程学院，北京 100044)

基于电磁场模型的轨道电路钢轨阻抗研究

朱 冰，刘中田，周 果

(北京交通大学 电子信息工程学院，北京 100044)

轨道电路能够传递列车行车许可、检查轨道占用，有效地保证了列车安全高效的运行。轨道电路的钢轨阻抗决定了轨道电路的传输性能，研究钢轨阻抗变化具有重要意义。本文提出一种基于电磁场模型的钢轨阻抗研究方法。首先分析轨道电路中钢轨阻抗的分布原理，确定钢轨阻抗的计算方法；然后建立模型，计算比较有砟轨道和无砟轨道钢轨阻抗在不同环境和频率下的变化；最后仿真验证无砟轨道钢轨阻抗优化方法的正确性。结果表明电磁场模型可以很好的模拟轨道电路，分析不同环境下钢轨阻抗的变化规律，验证了加高距离和绝缘方法对于优化无砟轨道钢轨阻抗的正确性。

轨道电路；钢轨阻抗；电磁场模型；相对磁导率；频率

轨道电路是CTCS系统中不可缺少的部分，它实现列车占用检查，生成行车许可信息，在保证列车安全运行的基础上有效地提高了运行效率，保障列车安全高效的运行。我国现行的ZPW—2000A无绝缘轨道电路是在法国UM71型轨道电路基础上设计实现的，其使用钢轨作为传输媒介，利用钢轨自身特点实现钢轨的绝缘效果，保证了轨道电路信号的顺利传输。轨道电路在不同的环境下钢轨阻抗会发生变化，并且无砟轨道中轨道电流与钢筋网存在互感作用，改变了钢轨阻抗的大小，使得电阻变大，电感变小，传输距离变小，影响了轨道电路的传输，因此要研究钢轨阻抗的变化规律，并且寻找方法缓解或者解决无砟轨道对轨道电路的影响，保证轨道电路信号的顺利传输[1]。

赵会兵[2]提出基于边界条件分析法的轨道电路数字仿真方法，并结合了VXI总线技术运用于轨道电路参数的测试中；毛广智，解学书[3]提出了matlab和simulink下的轨道电路的仿真结果；李元，丁万虎，王实[4]等提出了在LabVIEW软件平台下，构建了一款基于专业声卡的轨道电路钢轨阻抗测量系统实时测量轨道电路大小；高仕斌，卢涛，侯震宇等[5]推导出钢轨和两层无砟轨道板的电阻、电感以及两两之间的互感，计算出了钢轨阻抗与传输长度；禹志阳， 杨奎芳，申凤鸣[6]通过在秦沈客运专线轨道电路参数实测的基础上分析比较无砟轨道对轨道电路产生的影响。由于钢轨与钢筋网络之间存在互感作用，轨道电路处在一个电磁场环境中，因此建立电磁场仿真模型非常有用，不但能从轨道各部分的材质、周围的环境进行考虑还真正从对轨道电路传输产生影响的本质上进行建模计算。这是以上研究所没有的。

本文借鉴已有的研究成果，对60 kg/m的钢轨进行轨道电路电磁场建模。（1）分析轨道电路钢轨阻抗的分布情况，通过有限元方法对钢轨阻抗计算方法进行推导。（2）使用电磁场仿真软件建立轨道电路模型，包括两根钢轨的模型、有砟轨道的模型和无砟轨道的模型。（3）对比两根钢轨模型近场磁场强度的变化与电磁场原理是否一致，验证模型的正确性，改变模型中的参数，仿真计算有砟轨道和无砟轨道钢轨阻抗随频率和环境变化的规律。（4）通过分析无砟轨道钢轨阻抗的变化，仿真优化无砟轨道钢轨阻抗，保证轨道电路信号的有效传输。

1 轨道电路钢轨阻抗分析

轨道电路钢轨阻抗包括钢轨自身的阻抗和两根钢轨之间的互阻抗，阻抗由电阻和电感串联组成。钢轨阻抗电路如图1所示：

图1 等效钢轨阻抗电路

在不考虑邻线干扰的情况下，两根钢轨电压和电流之间矩阵关系为：

其中V2、V2为钢轨两端电压，I1、I2为钢轨中电流，R11、R22分别为两根钢轨的自电阻，L11、L22分别为两根钢轨的自电感，R11、R22分别表示两根钢轨之间的互电阻和互电感。

从能量的角度出发，钢轨中耗散功率Wd和储能Es分别为：

对于钢轨模型，分别加入共模和异模两种电流激励进行计算，其中对于共模电流I1=Iz，对于异模电流I1=_Iz。在理想状态下钢轨自身的阻抗相等，所以

英国R.J.HiII[7]借助有限元的方法，即将钢轨分割成多个小的单元，对于每一个小单元进行求解，然后对各个单元的耗散功率和储能进行叠加，得到整个模型的耗散功率和储能，由于各个单元上电流都是相等的，根据公式（4）～（7）可以求出钢轨自阻抗和互阻抗的大小，相加即可得到钢轨阻抗的最终结果。

通过建立电磁场模型，将模型分割成小单元进行有限元计算，可以很好地模拟钢轨周围的电磁场环境，计算钢轨阻抗的大小。

2 模型建立与仿真

本文使用Ansoft maxwell电磁仿真软件进行仿真，仿真的步骤如下。

2.1 建立物理模型

按照实际情况完成模型各部分的绘制，根据实际情况设置各部分材料参数。仿真中使用60 kg/m的钢轨，其电导率为900 000 S/m，相对磁导率为8.575，为了保证模型在计算中的有效性和收敛性，钢轨模型长度为1 m。对于有砟轨道和无砟轨道，参照它们的整体结构和所处环境，建立轨道电路所处的环境模型。因此，在有砟轨道仿真中，在钢轨下依次建立胶垫、枕木、道碴和大地模型，具体模型参数见表1所示：

表1 有砟轨道模型参数

在无砟轨道仿真中，钢筋型号为HRB500型，其电导率为800 000 S/m，相对磁导率为2 000，对于钢筋网络，为了简化计算，钢筋使用六面体代替圆柱体，由于钢筋尺寸相对较小，并且对形成的网络形状影响不大，所以不会对最后结果产生大的影响。在无砟轨道仿真中，在钢轨下依次建立带钢筋网的道床、橡胶垫、底座和大地模型，具体参数见表2所示：

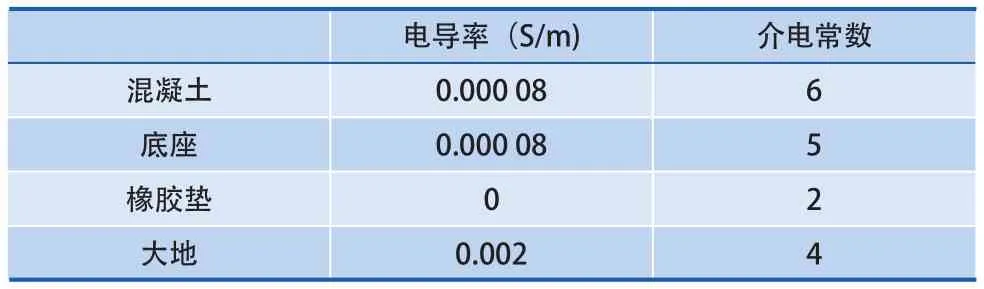
表2 无砟轨道模型参数

2.2 建立激励源模型

激励直接施加在钢轨截面上，沿钢轨分别进行共模和异模两次仿真进行计算。激励使用最大值为10 A正弦电流源，由于电流较小，保证钢轨和钢筋呈现未饱和状态，B-H曲线呈现线性分布。

2.3 仿真设置

对模型进行剖分，剖分网格大小会影响计算效率和准确性，要选择合适的网格大小；依据仿真需要设置正弦电源的频率参数。完成剖分和参数设置后即可进行仿真。

2.4 后处理

仿真完成后，可以查看钢轨近场处磁场强度的变化情况，验证模型是否正确，模型正确后即可使用仿真工具自带的计算器对需要求解的参量进行计算。

3 仿真结果分析

3.1 模型磁场强度分析

对于两根钢轨的模型在垂直于钢轨的截面上，在共模和异模激励下磁场强度分布如图2、3所示：

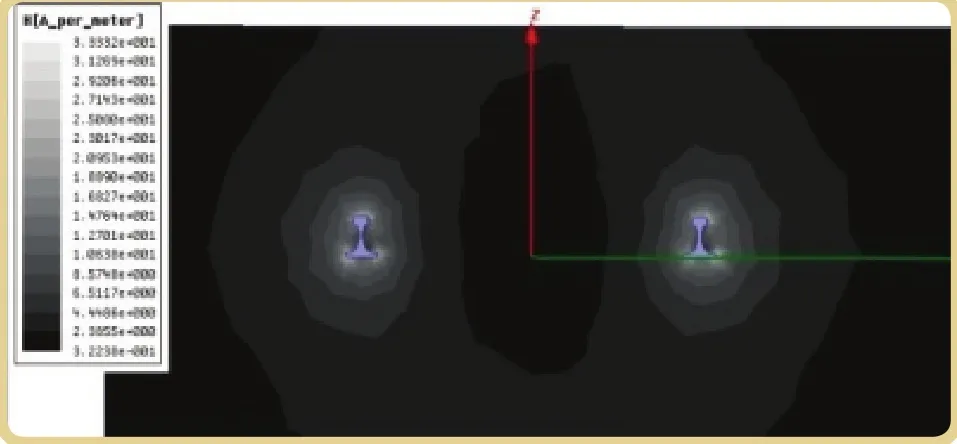
图2 共模激励下钢轨垂直截面上磁场强度

图3 异模激励下钢轨垂直截面上磁场强度

图2、3中，钢轨周围磁场强度最大，随着距离变大，近场磁场强度逐渐变小，围绕钢轨形成一个一个的环状。

在平行于钢轨传播方向，钢轨上方10 cm处即为TCR接收天线所在处，此处的磁场强度沿信号传播方向如图4所示：

图4 沿钢轨上方10 cm处磁场强度

图4中磁场强度呈现波动性，在长距离下具有正弦信号的状态。

通过分析两根钢轨模型在平行与垂直轨道上的磁场强度，仿真结果与理论上的结果一致，验证了模型的正确性。

3.2 钢轨阻抗分析

对于有砟轨道和无砟轨道模型，使用仿真软件自带的计算器对模型的欧姆损耗和储能进行体积分，使用公式（4）～（7）即可计算出钢轨阻抗的大小。

3.2.1 频率影响

当考虑频率对钢轨阻抗的影响时，在使用不同频率的正弦电源对模型进行仿真，计算结果如图5、6所示：

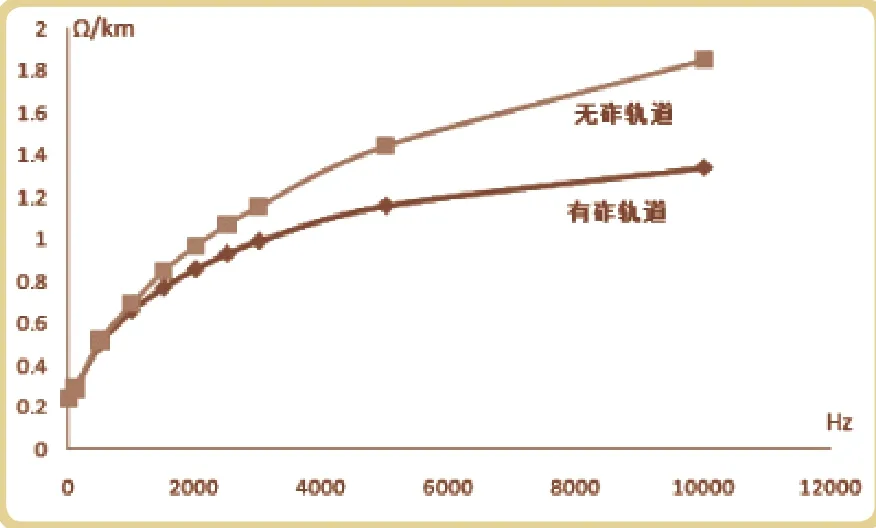
图5 钢轨电阻随频率变化

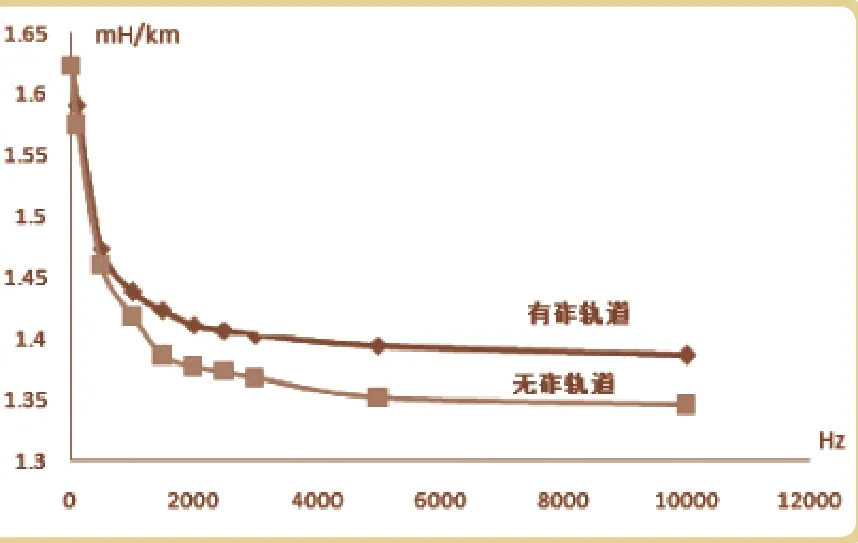
图6 钢轨电感随频率变化

由此可见，随着频率的增加，钢轨电阻逐渐增大，电感逐渐变小，在低频时变化比较明显，随着频率增大，变化越来越小。对比有砟轨道和无砟轨道钢轨阻抗结果发现当引入无砟轨道板时钢轨阻抗中的电阻增大了，电感变小了，在低频时差别较小，高频时差别较大。

3.2.2 大地磁导率影响

由于在不同的地质条件下大地磁导率会发生变化，不同土地成分会有不同的磁导率，所以要分析大地相对磁导率对钢轨阻抗的影响，计算结果如图7、8所示。

对比大地相对磁导率分别为0.8、1、1.2时钢轨阻抗变化可见，当大地的相对磁导率变大时，钢轨阻抗中电阻不变，电感逐渐变大了，在有砟轨道和无砟轨道中同样适用。

3.2.3 道砟磁导率影响

有砟轨道道砟在使用过程中会造成磨损，并

图7 大地相对磁导率分别为0.8、1、1.2时钢轨电阻随频率变化

图8 大地相对磁导率分别为0.8、1、1.2时钢轨电感随频率变化

且其干燥程度都会造成道砟磁导率的变化，在干燥环境和刚下过雨之后道砟磁导率会有很大的变化，所以要分析道砟相对磁导率对钢轨阻抗的影响，计算结果如图9、10所示。

由此可见，当道砟相对磁导率变大时，电阻在高频是会稍微变小，电感会变大，在相对磁导率在1以下变化比较明显，相对磁导率大于1时变化较小。

3.2.4 无砟轨道板影响

在无砟轨道中无砟轨道板的磁导率也会影响钢轨阻抗的大小，计算结果如图11、12所示。

由此可见，当无砟轨道轨道板相对磁导率变大时，电阻变大，电感也变大。

4 无砟轨道阻抗优化

图9 道砟相对磁导率分别为0.8、1、1.2时钢轨电阻随频率变化

图10 道砟相对磁导率分别为0.8、1、1.2时钢轨电感随频率变化

图11 轨道板相对磁导率分别为0.8、1、1.2时钢轨电阻随频率变化

图12 轨道板相对磁导率分别为0.8、1、1.2时钢轨电感随频率变化

对比有砟轨道和无砟轨道钢轨阻抗发现无砟轨道板的引入使得钢轨阻抗中的电阻增大了，电感变小了，这使得传输过程中损耗变大，仅仅依靠加入补偿电容的方法已经不能保证信号传输，所以要寻找合适的方法改变钢轨阻抗的大小，保证轨道电路信号的传输不受影响。由于无砟轨道中钢筋网络同钢轨中电流的互感作用引起钢轨电阻变大、电感变小，所以要采取措施减小它们之间的互感作用，在使用中我们采用增加钢轨与钢筋网距离、截断和绝缘的方法，由于仿真模型中钢筋网沿钢轨方向长度仅有1m，所以对于截断方法仿真不会有明显的效果。由于轨道电路载频频率为1 700 Hz ～2 600 Hz，使用其中的2 000 Hz对增高和绝缘的方法进行仿真。

加大钢轨和钢筋网之间的距离，可以减小两者之间的互感作用[8]，因此建立模型，将混凝土加高5 cm,而钢筋位置不变。实际中采用在横向和纵向钢筋交汇处进行绝缘处理，截断电流传播路径，在仿真中，为了仿真方便，我们采取让纵向钢筋网络上移5 mm的做法模拟交汇处的绝缘措施，仿真结果如表3所示：

表3 2 000 Hz钢轨阻抗计算结果

由仿真结果发现增大钢轨与钢筋网距离或者采取绝缘效果之后无砟钢轨钢轨电阻分量变小了，这减小了无砟轨道传输中的损耗。

当将这两种方法合在一起使用时，计算结果如表4所示：

表4 2 000 Hz无砟轨道加高绝缘后钢轨阻抗计算结果

通过对比有砟轨道和无砟轨道钢轨阻抗发现当同时使用这两种措施之后无砟轨道钢轨阻抗有了很大的变化，保证了轨道电路信号的顺利传输。

5 结束语

本文通过建立电磁场模型，分析比较了有砟轨道和无砟轨道在不同频率及环境条件下的钢轨阻抗变化规律，并仿真了无砟轨道轨道阻抗的优化措施，研究结果表明：

（1）钢轨阻抗随着频率增加，电阻增大了，电感变小了；随着大地磁导率增加，电阻不变，电感变大；

（2）对于有砟轨道，随着道砟磁导率增大，电阻在高频是会稍微变小，电感会变大；

（3）对于无砟轨道，随着轨道板磁导率增大，电阻变大，电感也变大。

本文获得了有砟轨道和无砟轨道钢轨阻抗的变化规律，并且验证了对无砟轨道钢轨阻抗进行优化的措施，以电磁场模型对轨道电路进行仿真，为进一步研究轨道电路的核心问题奠定了良好基础。

[1]李宜生，傅世善. 无碴轨道与信号轨道电路要互相适应[J]. 铁路通信信号工程技术， 2005， 24（2）：3-6.

[2]赵会兵. 高速铁路轨道电路数字仿真系统的研究[J]. 北方交通大学学报，1999，23（5）： 69-72.

[3] 毛广智，解学书. 轨道电路的建模与仿真[J]. 机车电传动，2004（1）：41-44.

[4] 李 元，丁万虎，王 实，王智新.基于LabVIEW的钢轨阻抗特性测量系统[J]. 测控技术，2012，31（7）：110-113.

[5] 高仕斌，卢 涛， 侯震宇，阮 阳. 无绝缘轨道电路对无砟轨道的适应性分析[C].电气化铁道 客运专线技术研讨会论文集，2006：248.

[6] 禹志阳，杨奎芳，申凤鸣. 轨道电路在无砟轨道条件下传输特性的研究[J]. 铁道学报，2007，29（5）：122-127.

[7] R.J.HiII. Railway track transmission line parameters from finite element field modelling: series impedance [J]. ElectricPower Applications, 1999,146(6): 647-66.

[8]霍宏艳，刘 刚，吴 晓.无砟轨道电磁特性仿真分析[J].铁道技术监督，2011，39（10）：44-50.

[9] 闻映红，周克生，等.电磁场与电磁兼容[M]. 北京：科学出版社，2010：108-110.

责任编辑 徐侃春

Study on track circuit impedance based on electromagnetic fi eld model

ZHU Bing, LIU Zhongtian, ZHOU Guo
( Electronic Information Engineering of Beijing Jiaotong University, Beijing 100044, China )

Track circuit could be used to transmit train movement authority(MA) and check the track occupancy, and it could effectively ensure the safety and efficiency of the train. The impedance of track circuit determined the transmission performance, so it was very meaningful to study on impedance of track circuit. This paper proposed the study method for track circuit based on electromagnetic fi eld model. First, the calculation of the rail impedance was determined. Secondly, the mode was established, the rail impedance was calculated in different environments and frequency. Finally, the correctness of the optimization non-ballasted track rail was certificated. The electromagnetic model of track circuit was proved to be a commendable simulation model of track circuit and the variation of the rail impedance in different environments was simulated. The correctness of the optimization non-ballasted track rail by heightening the distance or imposing insulation measures was certi fi cated.

track circuit; rail impedance; electromagnetic fi eld model; relative permeability; frequency

U284.2∶TP39

A

1005-8451（2014）05-0052-06

2013-11-29

中央高校基本科研业务费专项资金资助（2013JBM015）。

朱 冰，在读硕士研究生；刘中田，副教授。