Retrieval study of lake water depth by using multi-spectral remote sensing in Bangong Co Lake
Pu Zheng , ZhengDong Deng , Xin Ye
1. College of Defense Engineering, PLA University of Science & Technology, Nanjing, Jiangsu 210007, China
2. PLA 96528 Unit, Beijing 102202, China
1 Introduction
Water depth data is the basic data for water resources survey, water transport, water conservancy and marine research. Traditional water depth measurement methods use ground-based measurements such as a ruler or sonar,with a high degree of accuracy considering the heavy workload. Unfortunately the high cost of simultaneous water depth measurements cannot be used over a large area. The application of remote sensing data can retrieve water depth of large areas in a short period of time, circumventing the inefficiencies of traditional measurement methods, and has significant research value.
Water depth remote sensing technology is based on the propagation of electromagnetic waves in water,through a certain method to extract sediment reflectance spectra of the water contained in the remote sensing data,then retrieving water depth. Due to the limitation of electromagnetic wave penetration, the retrieval of water depth by remote sensing only can be used in clear and shallower water by multi-spectral remote sensing.
Water depth remote sensing studies began in the 1970s, with the development of satellite technology. The retrieval of water depth by remote sensing gradually developed from a qualitative analysis to quantitative analysis, and calculation algorithms also developed from empirical to semi-empirical model sand model algorithm based on the theory of radiative transfer (Lyzenga, 1978;Paredes and Spero, 1983; Spitzer and Dirks, 1987). The semi-empirical model of statistical correlation method was simple and easy to implement, being concerned by more people. Lyzenga (1977) further developed the multi-band method to extract water depth, and to some extent improved the accuracy of remote sensing detection.Philpot (1989) used a multi-band spectrum to extract water depth, along with irradiance single scattering as a cor-rection, thus further improving detection accuracy. The method of Panget al. (2004) took into account the influence of different water sediments by first partitioning the water sediment, and then retrieved the water depth, thus improving the accuracy of water depth.
The study area used in this article is Bangong Co Lake, using multi-spectral data and underwater terrain data, through pre-treated sample data to establish single-band, double-ratio-band, multi-band and BP network models for water depth retrieval. Stand-alone sample data is used to test those models, and then compare model performance quantitatively.
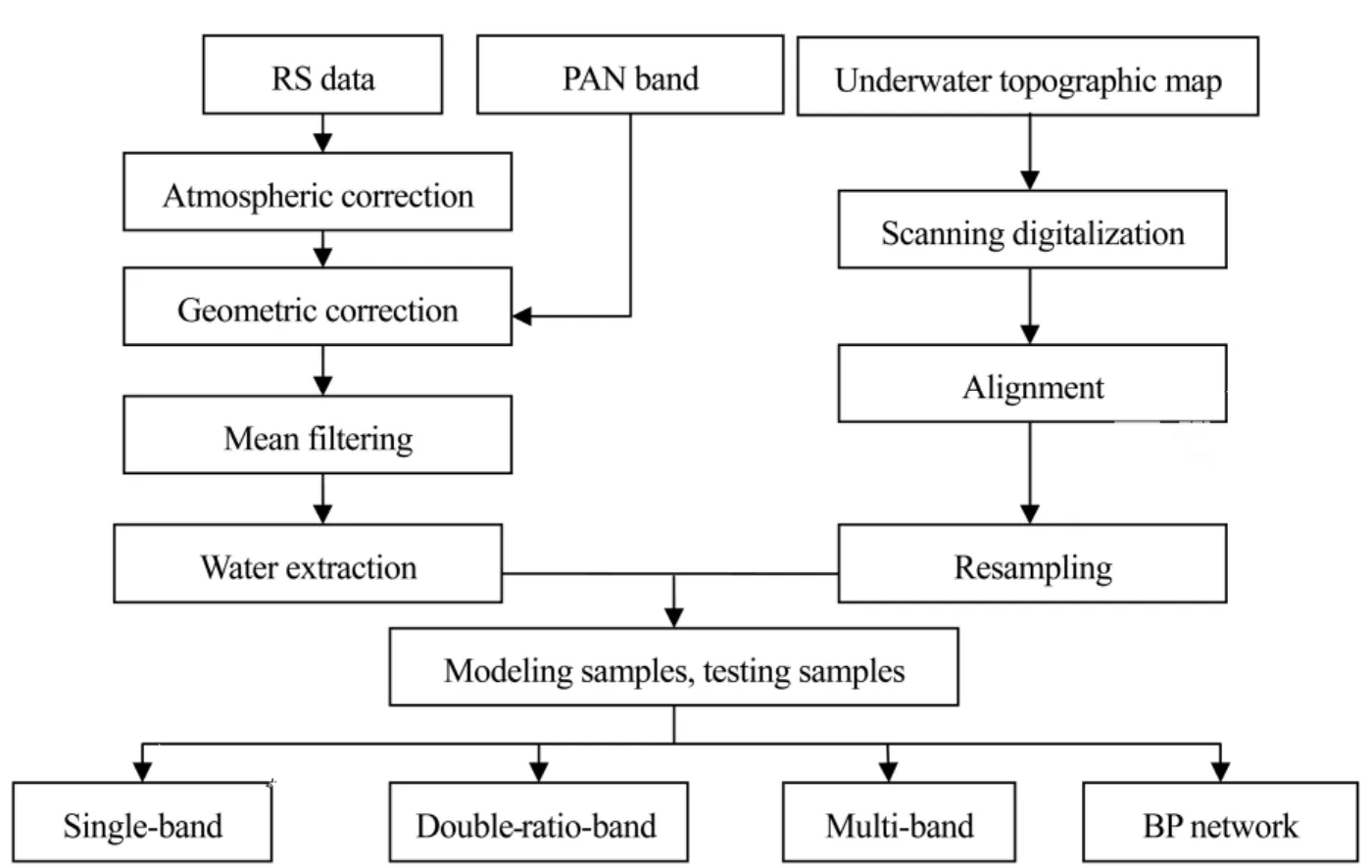
Figure 1 Research flow chart
2 The study area and data selection
2.1 Study area
Bangong Co Lake (33°25'N–33°39'N, 79°39'E–79°57'E), also known as Cuomuanglaren Bo, stretches across Rutog County, China’s Tibet Autonomous Region,and Indian Kashmir, within the deep fault structure of Bangong Co-Selin Co. The lake has a total area of 604 km2of which 413 km2resides in China, and measured maximum depth is 41.3 m. Lake District climate is dry and cold, and is one of the driest areas of the Qinghai-Tibet Plateau. Annual average temperature is -4 to-2 °C, average annual precipitation is 61.4 mm, evaporation is about 2,456.3 mm, and lake water replenishment is mainly from ground runoff. The study area includes all of Bangong Co Lake, which is divided into three regions,eastern, central and western, with the eastern region also called Anglarui Co (Figure 2).
2.2 Data selection
This study selected Landsat TM multi-spectral remote sensing data, with an imaging time of September 16,2002, solar elevation angle of 47.5°, and it was cloudless weather. Water depth data is derived from 1:100,000 underwater topographic maps which were measured from July to August, 2002. No major precipitation occurred during the study, and bottom lake erosion was minimal.Thus, remote sensing data and water depth data is synchronized, and can be used for further analysis. Because portions of the western region lack high precise topographic maps, this study relied on the PAN (panchromatic)band as the basis of geometric correction.
2.3 Lakewater depth measurement
Water depth was measured by use of a HD-27 digital single-frequency depth sounder with a GPS receiver (Haida Mapping Instrument Co., Ltd. Guangzhou, China). This sounder records instantaneous water depth (accuracy 0.01 m) and location (accuracy 0.01 s) with velocity set as 1,460 m/s. In fact, the speed of sound in water at different water depths are different, but because the Bangong Co Lake lacks information on the speed of sound at different depths and there is no sounder velocity correction, thus the same depth is used for sound velocity values. The underwater topographic maps were used, registered in Mapgis systems and vectorization, so that all isobaths equipped geographic coordinates, and can be modified.
By using the obtained vector, measurement data and modifying previous underwater topographic maps, we were able to produce a new underwater topographic map of Bangong Co Lake (Figure 3).
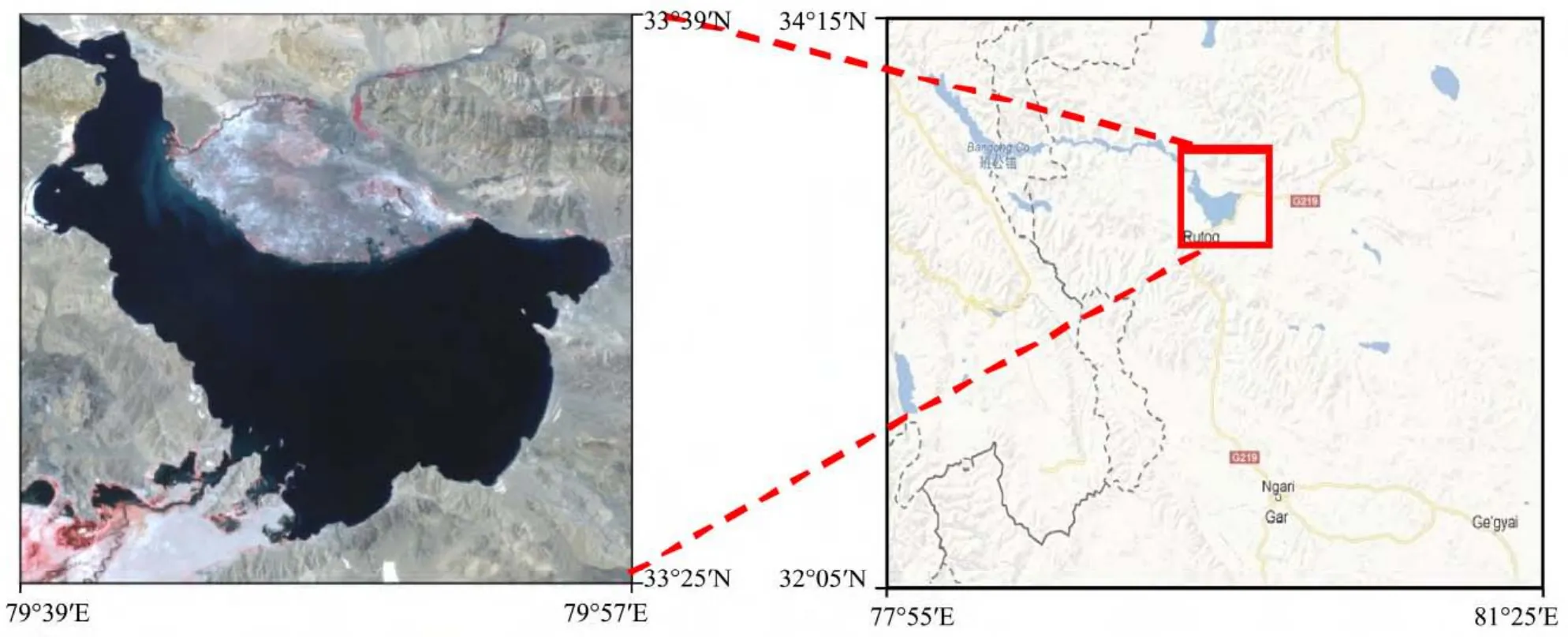
Figure 2 The study area
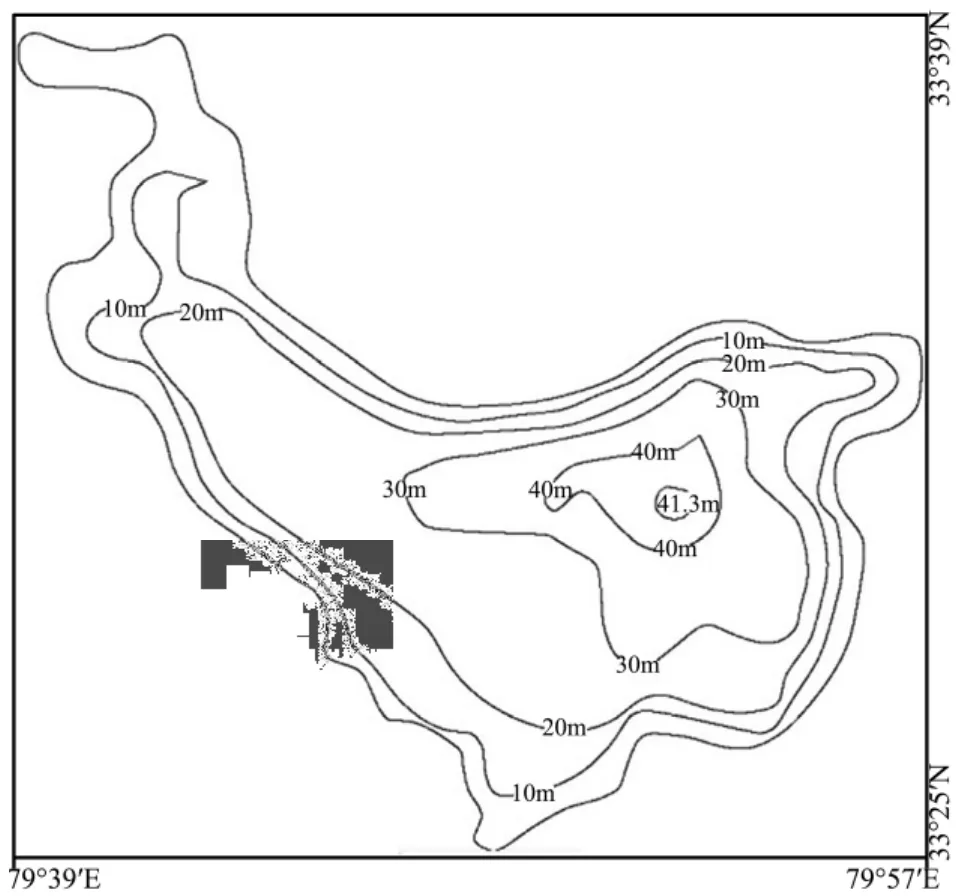
Figure 3 Underwater topographic map of the study area
2.4 Data preprocessing
2.4.1 Atmospheric correction
Dark pixel method is a classic method for atmospheric correction. Its fundamental principles are: assuming the existence of calibration dark pixels, Lambertian reflection of surface, and homogeneous atmospheric properties in remote sensing image. When ignoring the insignificant effects of atmospheric multiple scattering radiation and neighboring pixel diffuse emission, emission rate of dark pixels relatively increases due to atmospheric effects, which could also be attributed to the radiance produced by atmospheric effects. By subtracting these dark pixel values, we can reduce atmospheric scattering effects on the whole image, and obtain atmospheric correction. This paper uses dark subtract tool in ENVI software to acquire atmospheric correction.
2.4.2 Geometric correction
Due to influences of map projection method, change of exterior sensor elements, the uneven sensing medium,the Earth curvature, topography, and Earth’s rotation and so on, the remote sensing images exist certain geometric distortion compared with the target object. There is difference between the geometrical figures on image and projection, thus the image has distortion of geometric shape or position. To take advantage of a variety of remote sensing image analysis, we should first eliminate the distortion, therefore, geometric correction is an important part of remote sensing image processing. Geometric correction consists of three steps: first, selection of the control points; second, data space transformation based on the control point, which corrects geometric distortion error in the position; third, image resampling. This paper used PAN band as the baseline of Geometric Correction. The correct choice is a quadratic polynomial correction model, the control point for the 14 images is corrected by the geometry, geometric mean square (RMS Error) is less than 0.5 pixel, the overall error (total) is less than 1 pixel, and can be concluded that the selected ground control points meet the accuracy requirements.
2.4.3 Convolution enhancement
Image enhancement technique is the utilization of gray value of pixel operation in and around the pixel, to enhance the sharpness of the entire image. Convolution enhancement is the whole image block according to the average of pixel processing for changing the spatial frequency characteristics of the image. The key enhancement is the convolution operator, here we use the mean filter, also called low-pass filter, through which local noise has the maximum degree of reduction.
2.4.5 Water information extraction
Water indices are various in present studies. In this paper, We use the water extraction model of Yang and Xu(1998) as (TM2 + TM3)/(TM4 + TM5)>k.
As for different regions and different seasons, the threshold valuekis often not fixed, a specific test is needed to obtain images continuously, and the general value ofkis between 1 and 2. According to the water extraction model, using TM2–TM5 band data, spatial modeling in ENVI software modules for band computing,and the test obtains akvalue of 1.5 when the water extracts the best.
2.4.6 Alignment
The underwater topographic map is scan-digitized and alignment interpolated to the same resolution of remote sensing image. 368 points are selected and distributed on match point, 16 data outliers are removed, and the remaining 352 pairs of data are taken as sample data,of which 234 samples are used to establish the model of water depth, 118 samples are used as a stand-alone detection data. PAN band is then used to precise geometric correction of multi-spectral image; mean filtering is used to remove the multi-spectral image noise by the window of 3pixel×3pixel. Finally, the water index (TM2 +TM3)/(TM4 + TM5)>1.5 is determined for remote sensing image by the experiment.
3 Basic principle of water depth remote sensing
There are three types of multi-spectral retrieved depth models: firstly, physical analytical model, which has a definite physical meaning, but need more water parameters; secondly, statistical correlation method, through the establishment of water depth and value of statistical correlation to retrieve water depth; thirdly, semi-empirical semi-statistical model, which is a theoretical formula and can be simplified, and mainly includes single-band, double-ratio-band, and multi-band models.
3.1 Single-band model
Radiation propagation of light in the water is very complex, with numerous parameters that are difficult to measure, so the semi-theoretical and semi-empirical model was established, with a simplified formula of Wang and Gong (1983) as follows:
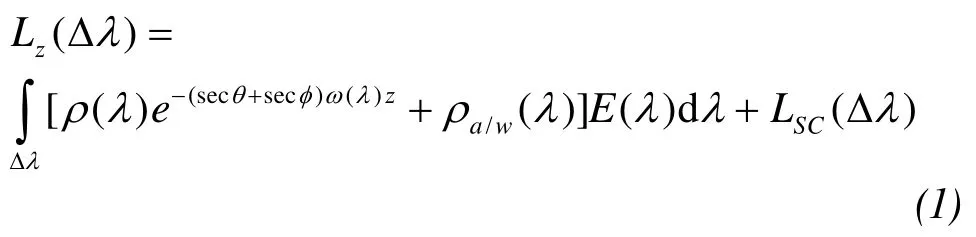
Lz(Δλ) is the spectral band Δλof radiation energy received from a sensor at depthZ;E(λ) is solar spectral radiation of water surface;ρa/w(λ) is water-air interface reflection rate;ρ(λ) is underwater reflection rate;LSC(Δλ)is the backscattering energy of water surface;ω(λ) is water attenuation coefficient;θis the zenith angle of observed sensor;φis solar zenith angle.
Because of the last two of formula(1), the calculation of water depth is imprecise, but this imprecision in deep water can be eliminated through remote sensing data. For any deep waters whenZ→ ∞ for the exponent ofein formula(1)should be zero, thus
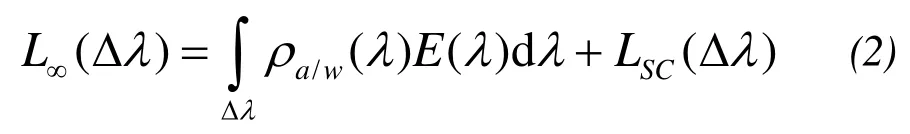
Subtracting formula(2)from formula(1):
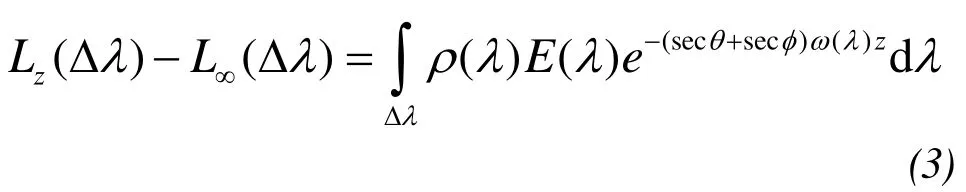
Assuming a narrow spectral band in satellite remote sensing, and satellite sensor output signal and incident energy are proportional, we obtain the following:
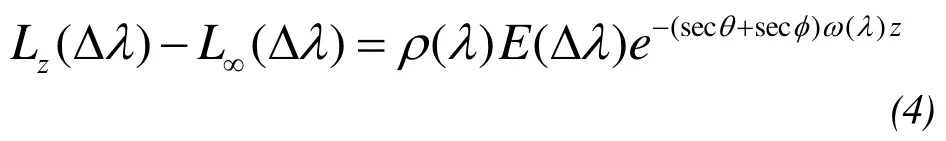
The model of single-band is:

where
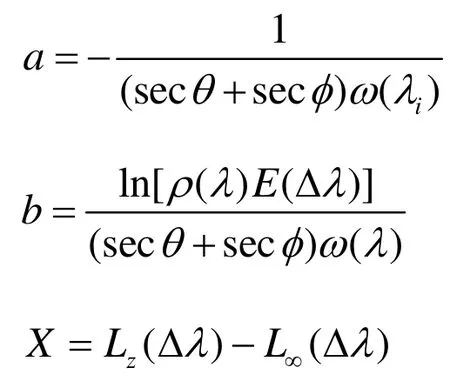
When water sediment type and water body optical properties have good similarity,ρ(λ) andω(λ) are constant,through regression analysis of the measured data, coefficientsaandbcan be obtained to retrieve water depth.
3.2 Double-ratio-band model
Numerous studies have demonstrated that underwater reflectance and water attenuation coefficient are very different in different sediment and water types. The underwater reflectance ratio of the two bands will not change without the influence of substrate types, and the attenuation coefficient of water is also more stable, so that the two band ratio can be used to retrieve water depth.
From formula(4), we can obtain:
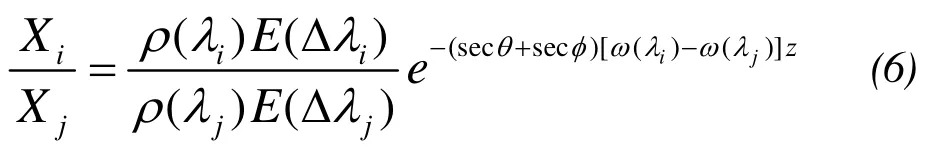
The double-ratio-band model is:
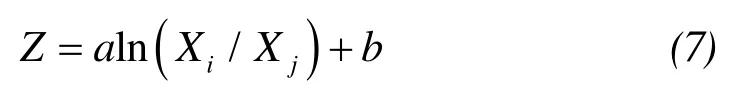
In formula(7), there are:
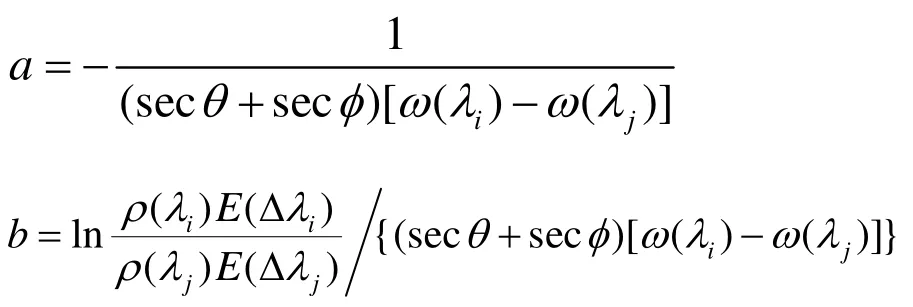
The double-ratio-band model can eliminate the impact factors of water depth retrieval to a certain extent,which is differences in water attenuation coefficients due to different water levels, and differences in lake bottom reflectance due to different sediment types. It can also weaken to a certain extent the influence of solar elevation angle, water fluctuation, satellite attitude and scan angle change to water depth retrieval.
3.3 Multi-band model
For practical applications, there is no homogeneous water and sediment, therefore, the application of simple attenuation model calculation would cause a large deviation with non-uniform sediment and great changes in water quality differences. Paredes and Spero (1983) developed a single-band model, and established a two-band model, assuming that the two bands are different in sediments A, B, ... on the reflectance ratio remains unchanged, for example:

Promotion(8)to:
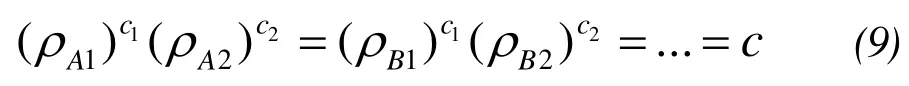
Logarithm on both sides
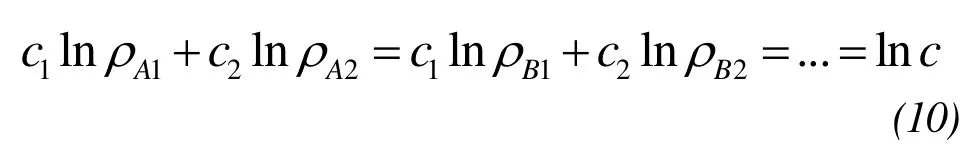
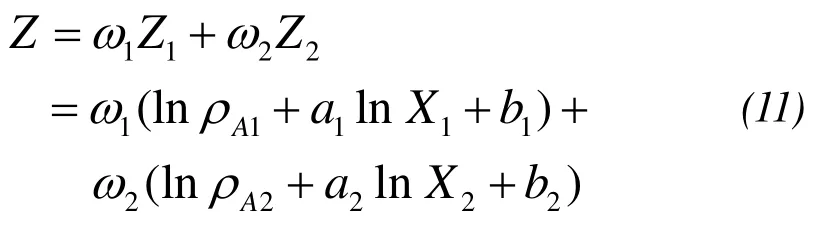
ω1,ω2are the weighting factors for the two bands and meetω1+ω2=1. Takeω1=c1/(c1+c2),ω2=c2/(c1+c2), substituted into the formula(11), plus(10)obtained:
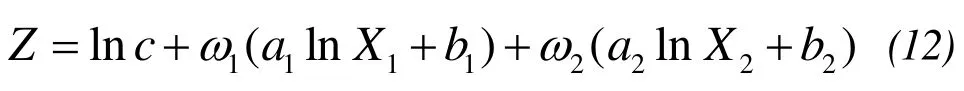
Simplified as:
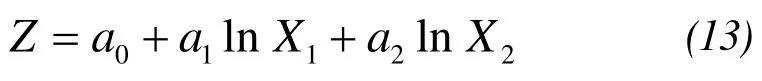
The dual-band model(11)is extended to the case ofndifferent band sand the numbernof different types of sediment, and ultimately can be obtained:
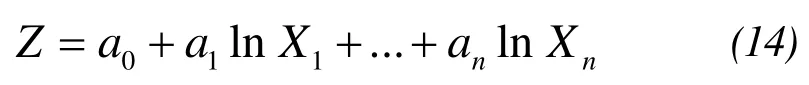
From the formula(14), due to introducedc1,c2, the sediment reflectance,ρA1,ρA2have been eliminated, it also means that water depth is regardless of sediment type.
3.4 Artificial neural network model
The artificial neural network has nonlinear characteristics, a large number of parallel distributed structure,learning and inductive capacity, and is widely used in many fields. Neural networks can provide a more effective solution for problems such as a lack of physical or statistical understanding, statistical variation in observed data, and the issue of data generated by nonlinear mechanisms.
Because the propagation of light in water is a very complex and non-linear process, it is difficult to use the laws of physics for analysis. Neural network is a kind of black-box model, it does not need to know the internal mechanism, it only requires a certain amount of band and bathymetric data to train and learn. The model also constantly adjusts the network connection weights by learning, and when the network output reaches a predetermined error range, it will stop training. A trained neural network for unknown areas will be able to predict water depth and the prediction accuracy and size of the effect depends on the good or bad of the training and generalization ability.
4 Water depth retrieval analysis results
Of the 352 samples obtained by the pretreatment data, two thirds of the samples are used for model construction, the remaining one third are used as an independent to detect the model. In order to quantitatively compare the model’s fitting effect, we select the following three statistical parameters to assess the model,the coefficient of determinationR2, mean absolute error(MAE) and root mean square error (RMS).
In these formulae,yiis measured water depths,is the model’s predicted water depth values,is average measured depth, andnis number of water depth samples.
4.1 Correlation analysis
Due to water absorption, light propagation in water decays exponentially, the larger the wavelength, the larger the penetration depth in the water. This study shows that the penetration depth of blue-green wavelength is the best, with TM1 band penetrating depth of more than 30 m, and TM2 band of more than 20 m. Because the deepest of Bangong Co Lake is 40 m, TM5–TM7 bands in the mid-infrared and thermal infrared wavelength range was basically completely absorbed by the water and thus lacked any water depth information. Here, we choose TM1–TM4 bands to retrieve water depth, and along with correlation analysis and results are presented in table 1.
In the single-band model, the correlation coefficient of TM3 with depth is 0.74, 0.60 for TM2, and 0.27 for TM1.The TM1 band is optimal for penetration and minimum attenuation in water, but reflectance spectra results of different water depths is not very different, coupled with lake wave noise provides minimal retrieval depth for the TM1 band. TM2 and TM3 band’s attenuation is larger than TM1 in water, but they reflect the difference of different water depths, and at the same time have the ability to penetrate the water, and therefore have a better correlation with water depth.
After band ratio, most of the correlation coefficients of the model with water depth increased, thus the band ratio method can effectively eliminate some factors to improve retrieval accuracy. TM3/TM1 correlation is 0.82,which has been greatly improved, compared with the single-band. Some tests show that TM4/TM2 and water depth have best correlation in clear water, but in this test the best is TM3/TM1, to the shortwave direction, the"blue shift". Bangong Co Lake water contains sediment,suspended solids and yellow substances which reduces the penetrating power of the spectral radiation in the water. Thus, TM4/TM3 correlation coefficient decreased,which stems from the two-band is long wave, and the retrieval error is larger in deep water regions. The correlation coefficient of multi-band model is 0.85, higher than the double-ratio-band model. Because the spread of light is influenced by many factors in water, multi-bands are introduced to reduce the influence of this interference.

Table 1 Single-band, double-ratio-band and multi-band inversion model correlation coefficients
4.2 The retrieval model of multi-band accuracy and evaluation
After correlation analysis, we selected TM3,TM3/TM1, and TM1–TM4 bands to establish the single-band, double-ratio-band and multi-band deep inversion models. 234 samples were used to establish a water depth regression equation, and then 118 independent samples were used for the regression equation test, with results presented in table 2.

Table 2 Single-band, double-ratio-band and multi-band retrieval model
4.3 The retrieval model of artificial neural network
The BP (Back Propagation) neural network is a local approximation network which can approximate any continuous function with very high precision. The networks basic idea of algorithm is that the learning process is of two processes, with forward propagation and error back-propagation of the signals. Forward propagation is descendant of the input samples from the input layer,treated by each hidden layer, passed to the output layer. If the actual output and the desired output layer do not match, it will transfer to the error back-propagation stage.Error back propagation output error in some form through the hidden layer to the input layer, layer-by-layer back propagation, and error apportioned to all the cells of the layers, then we can get the error signal of every cells in every layers, the error signal as a basis correction of every cells in the layer. The signal forward propagation weight and error back propagation layers adjustment process is repeated. Weights ongoing tuning process is the network’s learning and training process. This process continues until the network output error is reduced to an acceptable level, or until the preset number of learning.
TM1–TM4 bands are selected as input data, to build the BP model. The network structure has four input nodes and one output node, with 15 hidden nodes through testing. Here we choose the Sigmoid function. Momentum to the steepest descent method is selected to learn, with 25 training steps, training speed is 0.05, growth rate coefficient is 1.2, reduced factor of speed is 0.8, momentum factor is 0.9, number of training is 100, and training objectives is 0.1. After the BP structure is determined,TM1–TM4 bands are the input vector, the corresponding water depth data is the output vector, with 234 samples to train the network.
There are 118 samples used to test the neural network,with results presented in table 3. Compared with the multi-band model, the BP model performance is greatly enhanced, three quantitative indicators have improved significantly, and the neural network model to retrieve water depth has a great advantage.

Table 3 BP artificial neural network
5 Conclusion
According to the analysis and discussion of the aforementioned test results, the following conclusions can be drawn:
1) From the single-band model, double-ratio-band model to the multi-band model, the determination coefficient, the average absolute error and root mean square error is progressively smaller, which clearly reflect a trend that with the increase in the number of bands, the performance and effectiveness of the model improve sand the accuracy increases.
2) The BP model of remote sensing water depth retrieval is feasible. The MAE of BP model is 1.86 m,RMS is 1.98 m, and coefficient of determination is 0.87.Although this model cannot replace accurate depth measurement, it is an aid to wide range and rapid measurement in the same quality of water, provide strong support for ground measurements; it can also provide convenient for less precision survey.
3) The BP model is more precise than the traditional model effect at retrieving water depth by remote sensing.R2, MAE and RMS, three quantitative factors, indicate that the BP model’s performance is much better than the single-band, double-ratio-band and multi-band models,and should be widely applied to further research. Compared to the traditional model, there are shortcomings such as: the physical meaning is not clear, and requires too much training data on BP network model.
4) The retrieval model’s accuracy needs to be further improved. The propagation of electromagnetic waves in the atmosphere and water is a very complex process,with numerous influencing factors and noise from the mixture. If we want to extract precise water depth information, we need to: 1) pixel-accurate atmospheric correction, 2) study the impact of the solar spectrum radiation propagation by different water levels and sediment, which is the direction of future efforts.
This paper is supported by the projection of China Geographic Survey (12120113099800) and the projection of"863" (2012AA062601). The authors are very thankful to the PLA 68612 unit for providing water depth data.
Lyzenga DR, 1977. Reflectance of a flat ocean in the limit of zero water depth. Applied Optics, 16: 282–283.
Lyzenga DR, 1978. Passive remote sensing techniques for mapping water depth and bottom features. Applied Optics, 17: 379–383.
Pang L, Zhang MB, Zhang JX,et al., 2004. Shallow seawater depth retrieval based on bottom classification from remote sensing imagery. Chinese Geographical Science, 14(3): 258–262.
Paredes JM, Spero RE, 1983. Water depth mapping from passive remote sensing data under a generalized ratio assumption. Applied Optics, 22: 1134–1135.
Philpot WD, 1989. Bathymetry mapping with passive multispectral imagery. Applied Optics, 28(8): 1569–1578.
Spitzer D, Dirks RWJ, 1987. Bottom influence on the reflectance of the sea. International Journal of Remote Sensing, 8: 279–290.
Wang L, Gong JL, 1983. Remote Sensing—the development of remote sensing technology and its application. Canon Image Research Center. Science Press, Beijing.
Yang CJ, Xu M, 1998. Study on the water-body extraction methods of Remote Sensing information mechanism. Geographical Research,17(suppl.): 86–89.
 Sciences in Cold and Arid Regions2014年3期
Sciences in Cold and Arid Regions2014年3期
- Sciences in Cold and Arid Regions的其它文章
- Spatiotemporal variations of maximum seasonal freeze depth in 1950s–2007 over the Heihe River Basin,Northwest China
- Climate transformation to warm-humid and its effect on river runoff in the source region of the Yellow River
- Modeling tropical river runoff: A time dependent approach
- Water sources of plants and groundwater in typical ecosystems in the lower reaches of the Heihe River Basin
- Effects of fertilization on population density and productivity of herbaceous plants in desert steppe
- Effects of sand burial on dune plants: a review
