背景流中海洋内波垂向结构的计算和分析*
邓 冰,张 翔,张 铭
(1.北京应用气象研究所,北京 100029;2.海军海洋水文气象中心,北京 100079;3.解放军理工大学 气象海洋学院,江苏 南京211101)
海洋内波在海洋中非常常见,是发生在密度稳定层化海水中的一种波动,其最大振幅出现在海洋内部,是重要的海洋中尺度现象。海洋内波的存在,使得海水运动以及水文要素的分布与变化更加复杂。由于内波发生机制的复杂性以及时空特征的随机性,内波成为海洋学研究中的难点。鉴于海洋内波在海洋学和军事上的意义,目前已经成为研究的活跃领域。对海洋内波垂向结构的研究不但有重要的理论意义,而且有广泛的应用价值。
国内外许多学者对内波垂向结构问题作过分析与计算,如Fligel[1]利用Thompson-Haskell方法计算了内波的垂向结构;Haskell[2]利用分层计算对内波的垂向结构做过分析;Pereskokov[3]和 Leblond[4]等研究了不同海域内波的垂向结构。国内学者蔡树群等[5]采用Fligel的方法,求解了内波的垂向结构;近年来他们还发展了一个二维孤立内波的传播模式,系统研究了南海北部孤立内波的传播与演化规律[6];章克本等[7]借鉴俄罗斯学者的变换方法,得到了内波的垂向结构及色散关系。叶春生等[8]探讨了内波垂向结构的分段求解方法。在以往的海洋内波垂向结构的工作中,基本上是只针对波动本身的研究或对海洋内波垂向结构计算方法的讨论,很少涉及背景流对海洋内波垂向结构的影响。当海洋内波在水中传播时,往往会伴随有背景流的存在,所以把波和流放到一起进行研究是非常必要的。本文章提出了在垂直切变背景流中计算海洋内波垂直结构的方法,并给出了计算结果。
1 数学模型
研究海洋内波可采用以下无粘绝热的不可压方程组:

式中,z轴垂直向上,动力学变量u,v,w分别为水平和垂直速度的三个分量;热力学变量ρ,T,S,p分别为密度、温度、盐度和压力;ρ0,T0,S0分别为其标准值,取为常数;f是地转参数,对内波问题其可设为常数;微商算子
方程组满足以下边条件:
在海底:

在海面采用刚盖近似。
在海面:

式中,H为海洋水深,本研究不考虑海底地形,故H可设为常数。
在方程(1)中引入水平背景流U,并设该背景流的流向与x轴有一个常数夹角δ,而其流速U仅随高度z变化而流向不变,即有U=U(z),此时有u=Uzcosδ,v=U(z)sinδ,u,v则分别为该背景流U在x轴和y轴上的分量,且du/dz,dv/dz仅为z的函数。
引入此背景流后,则动力学变量有:u=u(z)+u′(x,y,z,t),v=v(z)+v′(x,y,z,t),w=w′(x,y,z,t)。这里u′,v′,w′为速度场对该背景流(基本流)的偏差,将其代入方程组(1)中,并将热力学变量分为背景场以及对该场的偏差,则可引入温度偏差T′、盐度偏差S′、密度偏差ρ′和压力偏差p′,此时有:T=T(x,y,z)+T′(x,y,z,t),S=S(x,y,z)+S′(x,y,z,t),ρ=ρ(x,y,z)+ρ′(x,y,z,t),p=p(x,y,z)+p′(x,y,z,t)。再考虑到背景场满足原方程,且因背景场不随时间改变,故背景流场在水平方向满足地转平衡,垂直方向满足静力平衡,热力学变量的背景场满足状态方程;这样就可得到以下关于偏差的状态方程:ρ′=ρ-ρ=ρ0·(-αT′+γS′)。在此ρ0为平均海水密度,设为常数。
本研究仅讨论准二维内波。设该内波沿x方向传播,即内波的波峰线与x轴垂直(此时该内波的传播方向与背景流的方向有夹角δ)。在波动振幅较小时,此时以上带“′”的物理量可看作小量,其二阶以上乘积则可略去。假设速度u′,v′,w′在y方向无变化,即∂u′/∂y=0,∂v′/∂y=0,∂w′/∂y=0;这样方程组(1)线性化后为:

在公式(4)中为书写方便以下已记 (u,v,w)≡ρ0(u′,v′,w′),p≡-gρ′,g为重力加速度,设为常数;在得到方程组(4)时还用到了“地转流”公式[9],求导后可得是层结参数;此时ρ(z)可认为是垂直方向上密度分布的典型值,其仅为z的函数。这样du/dz,dv/dz则均为z的函数。由(4)中最后一式可引入流函数Ψ,此时有u=∂Ψ/∂z,w=-∂Ψ/∂x,这样方程组(4)可写为:


对沿x方向传播的内波,可设方程组(5)的解即特征波动为:


此时,边条件可写为

这样方程组(8)与边界条件式(9)就构成一个变系数复常微分方程组的特征值问题。
2 数值计算方案
当背景流为非常数时,即背景流为z的函数时,解析求解上述特征值问题是非常困难的。数学上的困难阻碍了人们对内波物理本质的分析。随着计算机技术的迅速发展和应用,可通过数值方法求解上述特征值问题,具体方案如下所述。
将区间[0,H]等距分为M个子区间,即将其分为M层,并采用交错网格,将Ψ写在整数层网格点上,P、V写在半数层网格点上,如图1所示,此时微分方程组(8)可离散化为差分方程组。令X=(X1,X2,…,Xj,…,XM)T,其中则可将以上微分方程组的特征值问题离散化为复矩阵的广义特征值问题来数值求解,即有

这里,σ为特征值,X为特征函数(谱函数,也即特征波动的垂直结构);而A,B都是(3M-1)×(3M-1)阶的的矩阵,且B为复矩阵。

图1 垂直离散分层示意图Fig.1 Schematic diagram of vertical discrete layering
3 数值计算方案的验证
为验证以上数值计算方案的合理可行和编程的正确,本文章利用在特定条件下得到的解析解与计算解进行比较。当背景流和层结参数为常数时,则方程组(8)退化为常系数常微分方程组,与边界条件(9)所构成的特征值问题可得解析解。
3.1 背景流为常数海洋内波的垂向结构
当背景流为常数且取层结参数为常数时,此时易解析求解,并得到海洋内波σ的表达式,即频散关系为:

此时,以上数学模型中仅包含海洋内波(性质属重力惯性内波),这里m取值为自然数,为该海洋内波的模态数。这种情况下也易解析求得海洋内波的谱函数结构,即各物理变量特征波动的垂向分布:

式中,为任意常数。这时,随着模态数m的不同,特征值σ的数值也不同。因m是自然数,呈离散分布,故此时海洋内波各模态特征值σ的分布也是离散的,即该特征值问题仅有离散谱。由式(11)还可知,若层结参数>0(层结稳定),则σ为实数。此时,式(11)中仅包含有一对传播方向相反的海洋内波(重力惯性内波),其振荡频率为σ1和σ2,该频率的大小处于f和N0之间;且由公式(12)可知,流函数Ψ的振幅在海洋内部达到最大,在上、下边界则为0。
3.2 方案验证的结果
为比较海洋内波σ(特征值)的数值解和解析解之间的误差,这里设无背景流,即取=0=0;并取层结参数=1×10-5s-2,取地转参数f=8×10-5s-1;取海洋深度H=2 000m,取海洋内波水平波长L为20 km(此时k=2π/L)。采用以上数据,利用公式(12)求取解析解;利用以上数值方法求取数值解(取分层数M=40)。从而对解析解和数值解进行比较。
图2为前20个模态σ数值解对解析解的误差,即Ψ(z),此时其为实数。数值解与解析解的差值随海洋内波模态数m的分布。由图可见,前几个模态误差较小,随着模态数的增加,数值解的误差增大。但前20个模态的误差均小于6%,这表明数值解与解析解两者还是吻合得比较好的。
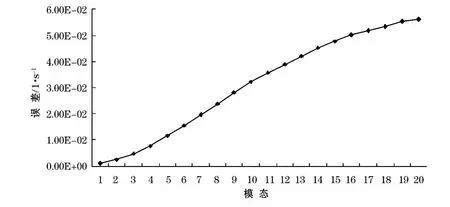
图2 计算解特征值误差Fig.2 The error of the computational solution eigenvalue
下面给出此时前5个模态数值计算得到的流函数振幅的垂直分布,即。流函数振幅第1模态为半个正弦波分布,仅有1个振幅最大值,出现在海洋中部;除边界外,无0点(图3a,以下所指的0点均为除边界外的海洋内部0点)。第2模态为一个正弦波分布,有2个极大值和1个0点(见图3b)。第3模态为1个半正弦波分布,有3个极大值和2个0点(图略)。第4模态为2个正弦波分布,有4个极大值和3个0点(见图3c)。第5模态为2个半正弦波分布,有5个极大值和4个0点(图略)。总之,Ψ的垂向分布为正弦波的形式,随着模态数的增加,该振幅极大值的数目增加,而0点数目也在增加;这表明,模态越高,其垂向结构就越复杂。以上的数值计算结果与解析解的表达式(12)完全一致。
该结果还表明,上述数值计算方案是合理可行的,在模态数不十分高的情况下,其精度也令人满意。

图3 无背景流场时不同模态流函数振幅的垂直结构Fig.3 The vertical structures of the stream function amplitudes of different modes without background current field
4 垂直切变背景流下内波的垂向结构
4.1 内波垂向结构的计算结果
现设内波传播方向与背景流的流向相同,均为x方向,即取夹角δ=0;此时有;再设基本流速在垂直方向呈线性变化,最大值在海面z=H处,为=0.2m/s,最小值在海底z=0处,为=0m/s。在这里的数值计算中,其他所用参数仍取上节中的值。在以上条件下,数值求解得到的V(z),P(z),Ψ(z)和Ψ则均为实数。

图4 线性变化背景流下不同模态流函数振幅的垂直结构Fig.4 The vertical structures of the stream function amplitudes of different modes with a linear background current
图4为在以上垂直线性变化背景流下,数值计算得到的流函数垂向结构Ψ的前20个模态的分布图。图中前9个模态的垂向分布与无背景流的流函数垂向结构Ψ各模态的分布相似,都具有光滑的波动特性,垂向结构无奇性,不存在Ψ的间断,这表明不存在临界层;此时由于该垂向结构受垂直线性切变背景流的调制,其不再呈标准的正弦波结构,而有所变形。从第10模态开始,流函数的垂向结构不再具有光滑的波状特性,而存在奇性,即有间断出现,而在该间断处出现了临界层。在该临界层(该间断)之上,其呈指数变化,在之下则呈波状变化;此时Ψ的最大值出现在临界层之下的近处。随着模态的增加,临界层的深度在加深。从计算得到的σ值看,均有σ>0,故其均为顺背景流传播的波动。

图5 线性变化背景流下不同模态速度函数振幅的垂直结构Fig.5 The vertical structures of the velocity function amplitudes of different modes with a linear background current
图5为V前20个模态中的部分模态的垂向结构分布图。图中前9个模态的垂向结构也无奇性,具有光滑的波状特性。第1模态最大值出现在上边界,第2模态则其出现在海洋中部,并有2个0点,随着模态的增加,0点增多。从第10个模态开始,V在Ψ临界层的深度处也出现了临界层,此时V的最大值也出现在该临界层之下的附近处。
4.2 讨 论
本文章因将一个常微分方程组的特征值问题离散化为复矩阵的广义特征值问题来进行数值求解,故其计算结果形式上都为离散谱。在以上数值计算中,在增加分层数M后,则可判断原常微分方程组的特征值究竟是离散谱还是连续谱[10,11]。原模态1~9在增加分层数M后谱点数无加密现象,故其确为离散谱;而模态11~20在分层数M增加后有谱点数加密(其特征值数目增多),故此时σ应为连续谱。这表明在原常微分方程组特征值问题中,其σ是连续分布的,而以上的数值计算则因离散化将其歪曲为离散谱。海洋内波的连续谱模态因存在间断,表面看来其似乎无物理意义(流函数应连续),不过该海洋内波连续谱所有模态的和是连续的(这里的和是指积分,在数值计算时可用求和来近似),并也满足方程组(8)和边界条件(9);而该积分则为海洋内波波包,在实际海洋中是有物理意义的。至于海洋内波波包在海洋动力学中扮演的角色和其作用,则目前这方面的工作尚不多见,值得深入研究。
当背景流存在垂直切变时,从以上数值计算的结果看,其传播频率既存在σ>0的顺背景流传播的海洋内波,也存在σ<0逆背景流传播的海洋内波。两个传播方向相反的海洋内波其形态大体相似(图略)。这里就不再给出计算结果和进行讨论。在方程(11)的解析解中也存在方向相反的两类波动,数值解也体现了这一性质。另外,本文章虽将地转参数f设为常数,但当存在垂直切变背景流时,因背景流有背景涡度存在,该涡度则会产生类似β效应的结果,故会有涡旋波出现。海洋内波(重力惯性内波)和海洋涡旋波是两类性质不同的波动,前者是非平衡的,后者是准平衡的。在本文所取参数下,这两类波动是完全可分的。本文为了突出讨论背景流对海洋内波垂向结构的影响,对海洋背景流和层结分布均做了简化,而实际海洋中背景流的垂直变化是复杂的。本研究结果仍可作为其一种定性近似。
5 结 语
了解某一海域海洋内波的垂向结构是海洋内波研究的一项基础性工作,在海水密度垂向层结状况分布较简单,且不考虑海水流动时,取地转参数为常数的情况下,则易通过解析解得到其垂向结构,此时该结构为标准简谐波;但对密度垂向分布较复杂,且存在背景流的情况下,解析求解几乎不可能。本文章利用线性、无摩擦、不可压情况下的旋转流体方程组,讨论水平方向运动呈一维状态的海洋内波。基于数值计算的方法,对背景流中海洋内波各个模态垂向结构做了分析,并在特定条件下,把数值解与解析解做了对比计算。结果表明,在无背景流时,数值解在不太高的模态下精度较高。海洋内波的垂向结构为简谐波的形式。模态数越高,在垂直方向的结构就越复杂,这时其模态均属海洋内波的离散谱。在有背景流垂直切变时,海洋内波的前几个模态仍与简谐波类似,只不过因受背景流的调制,其波形与标准简谐波有所变形,此时这些模态仍属海洋内波的离散谱;而在此之后的模态,其垂向结构不再光滑连续,而是出现了间断,即出现了奇性,该间断处即为临界层,此时的模态属海洋内波的连续谱(在本文数值计算中其被歪曲为计算离散谱),其解为广义解。而对该连续谱的垂直积分则可得到内波波包,其是有物理意义的。
(References):
[1] FLIGEL M,HUNKINS.Internal waves dispersion calculated using the Thompson-Haskell method[J].J.Phys.Oceanogr.,1975,5(3):541-548.
[2] HASKELL N.The dispersion of surface waves on multi-layered media[J].Bull.Seism.Soc Amer,1953,43(1):17-34.
[3] PERESKOKOV A.Density stratification and dispersion relation for internal waves in the North Atlantic[J].Oceanology,1984,24:566-569.
[4] LEBLOND P H,MYSAK L A.Waves in the ocean[M].Amsterdam:Elsevier Scientific Publishing Company,1978.
[5] Cai Shenqun,Gan Zijun.A numerical method of internal waves dispersion relation[J].Tropic oceanology,1995,14(1):22-29.蔡树群,甘子钧.内波频散关系的一种数值解法[J].热带海洋,1995,14(1):22-29.
[6] XIE J S,CAI S Q,HE Y H.A continuously stratified nonlinear model for internal solitary waves in the northern South China Sea[J].Chinese Journal of Oceanology and Limnology,2010,28(5):1040-1048.
[7] ZHANG K B,GAO H S.A numerical method for vertical structure of internal waves in ocean[J].Tropic oceanology,1997,16(4):62-67.章克本,高虎山.海洋内波垂向结构的一种数值解法[J].热带海洋,1997,16(4):62-67.
[8] YE C S,SHEN G G.A subsection solution to the vertical structure of internal waves[J].Journal of Tianjin University,2004,37(12):1041-1045.叶春生,沈国光.内波垂向结构的分段求解方法[J].天津大学学报,2004,37(12):1041-1045.
[9] BENOIT C R,BECKERS J M.Introduction to Geophysical Fluid Dynamics Physical and Numerical Aspects[M].New Hampshire:ACADEMIC PRESS,2009:37-57.
[10] ZENG Q C,LI R F,ZHANG M.Spectra and spectral functions in rotating two dimensional compressive motion part I:Distribution of spectra[J].Journal of Atmospheric Sciences,1990,14(2):129-142.曾庆存,李荣凤,张铭.旋转二维可压缩流动的谱和特征函数 -I:谱点分布[J].大气科学,1990,14(2):129-142.
[11] ZENG Q C,LI R F,ZHANG M.Spectra and spectral functions of rotating two dimensional compressive motion part(Ⅱ):Structure of spectral functions and further discussion on spectra[J].Journal of Atmospheric Sciences,1991,15(1):1-15.曾庆存,李荣凤,张铭.旋转二维可压缩流动的谱和特征函数II-谱和谱函数结构的分析[J].大气科学,1991,15(1):1-15.

