电动汽车充电站入网谐波分析

赵 伟 ，姜 飞 ，涂春鸣 ，肖 勇 ，孟金岭 ，肖 凡

（1.广东电网公司电力科学研究院，广东 广州 510080；2.湖南大学 电气与信息工程学院，湖南 长沙 410082）

0 引言

由于传统汽车尾气排放及石油危机等原因，各国对电动汽车的开发、普及势在必行［1-3］。然而，为满足电动汽车电池充电需求而投入的电动汽车充电站中的充电机，其工作时会产生大量的谐波，导致谐波污染［4］。分析电动汽车充电过程对配电网的影响已成为许多电力科研者关注的焦点。

采用电力电子技术的大功率充电机是一种高密度非线性用电设备，大量充电机（站）的投入将对电网提供的优质电能质量造成不利影响。而与普通谐波源相比，由于受充电站内充电机运行台数及不同电动汽车充电模式（慢速充电模式和快速充电模式）不断变化的影响［5］，充电站谐波输出特征更加复杂，且当城区内电动汽车充电站大量建设后，宽频域新类型谐波特征更加凸显，系统中高频谐波含量将不断升高［6-7］。

目前，针对电动汽车充电站的谐波研究主要集中在谐波抑制方法［8-11］，已有研究表明，获取谐波对电网影响最直接有效的方法是进行电网谐波潮流计算［12-15］。 此外，也可采用统计学知识［16］或建模理论［17］分析两者关系，例如文献［11］通过建立三相桥式不可控整流充电机、12脉波整流充电机、脉冲宽度调制（PWM）整流充电机的仿真模型，对其数据进行了详细的分析。文献［18］系统地总结了电动汽车充电应考虑的主要因素，并分析了电动汽车有序充电及与电网互动的研究现状和应用难点。同时，研究普遍认为配备谐波治理装置的电动汽车充电站对电网的影响应满足GB/T14549—1993《电能质量公用电网谐波》的要求［19］。但是，在进行谐波潮流计算过程中，考虑输电线路分布电容及变压器杂散电容的影响，谐波电流可能产生谐振放大现象。为避免此类情况发生，需对电动汽车充电站注入配电网的谐波电流大小进行严格监测与控制。可见，结合输电线路分布电容，深入分析电动汽车充电站谐波特点，明晰其对配电网各节点电压、电流的影响十分必要。

针对以上问题，本文建立了三相不可控整流充电机模型，分析了多组充电机谐波特征，并依据电力网络知识，针对电动汽车充电站中充电机所产生的谐波问题，结合线路的分布参数特性，利用双曲函数表示π型等值电路，定量描述了电动汽车充电站谐波注入对配电网电压、电流的影响。最后，以IEEE 14节点系统为例，验证了所提方法的科学性和有效性。

1 电动汽车充电站谐波分析

1.1 单台三相不可控整流充电机模型

电动汽车充电机是一种非线性设备，工作时产生的谐波电流很高。目前，使用最多的是由三相不可控整流电路与DC/DC功率变换器构成的充电机，其具有成本低、谐波含量高等特点［11］，典型结构见图1。其工作原理是三相不可控整流电路对三相交流电进行整流，经由电阻Rf、电感Lf和电容Cf组成的滤波电路后为高频DC/DC功率变换电路提供直流输入，经输出滤波电路后为电动汽车蓄电池提供电源［5］。

图1 高频充电机结构图Fig.1 Structure of high-frequency charger

虽然动力蓄电池的充电过程很长，但在一个微元ds中可以认为充电机的输出电流I0和输出电压U0是恒定的，即可用1个电阻R来近似模拟高频功率变换电路的等效输入阻抗［11，20］。

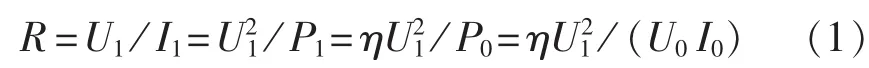
其中，U1、I1和P1分别为高频功率变换电路的输入电压、电流和功率；U0、I0和P0分别为高频功率变换电路的输出电压、电流和功率；η为功率变换模块效率。本文所取研究对象为充电过程中某一时刻，即直流侧电压U1为514.8 V、充电机电流I1为17 A、等效输入电阻R为32.63 Ω。

图2为单台不可控整流充电机交流侧电流波形，谐波电流畸变率达到了54.55%，奇次谐波电流较大，其中，5次谐波电流达到了8.17 A，7次谐波电流达到了4.44 A，11次谐波电流为1.4 A，13次谐波电流为1.15 A。可见，不可控充电机将产生较大的谐波电流，需进行治理。

图2 单台三相不可控整流充电机交流侧电流波形Fig.2 AC-side current waveform of uncontrollable three-phase rectifier charger

1.2 多台充电机谐波特征分析

现行的6脉冲不可控整流充电机产生的谐波次数主要为 6 k± 1（k=1，2，3，…），电网侧谐波总畸变率约为30%［8］。电动汽车充电站内往往含有多台充电桩，因此对于多台充电机的谐波特性研究十分必要。含有多台充电机及有源电力滤波器（APF）的充电站与电网连接示意图如图3所示。

图3 电动汽车充电站与电网连接示意图Fig.3 Schematic diagram of EV charging station connecting with power grid

当多台充电机同时工作时，配电网输入充电站的总电流为多台充电机输出总电流之和。由于各充电机在不同时刻工况不同，因此产生的谐波电流交互影响，或叠加或抵消。6台不可控整流充电机进行谐波治理前后的谐波电流大小如表1所示。由表1可知：谐波治理前，6台充电机并入电网后的电流畸变率为42.74%（低于单台充电机并入电网后的电流畸变率），其中，5次谐波电流达到了38.88 A，7次谐波电流达到了18.015 A，11次谐波电流为8.649 A，13次谐波电流为4.961 A；谐波治理后，各次谐波电流明显降低，谐波总畸变率为4.835%，符合电网谐波治理标准。但是，治理装置对不可控整流充电机产生的部分25次以上的高次谐波治理效果并不明显（由于治理装置接入的影响，其中部分高次谐波反而会增大）。若这部分谐波流入电网，与电网相互作用后可能出现新的特征，下文将进一步研究。

2 电网谐波潮流计算

由以上分析可知，电动汽车充电站多组充电机整流模块产生的谐波电流虽经变压器降压流入系统，但研究发现系统流动的谐波电流受线路分布电容影响后，可能引起放大现象。因此，对1.2节所述注入系统的高次谐波进行分析，有助于进一步了解电动汽车充电站接入电网后对系统各节点电压、电流处的精确描述。

表1 谐波治理前后，6台三相不可控整流充电机的谐波电流Table 1 Harmonic currents before and after harmonic suppression for six uncontrollable three-phase rectifier chargers

2.1 配电网谐波潮流模型

在谐波潮流计算中，谐波电压是由谐波源的该次谐波电流和其他节点上的谐波源的该次谐波电流共同作用于系统的谐波阻抗所产生。系统导纳矩阵中线路、发电机、变压器等谐波阻抗详见文献［21］，则第n次谐波电流为：

其中，In为节点注入的第n次谐波电流；Un为节点谐波电压；Yn为系统导纳矩阵。已知各谐波电源向系统注入的各次谐波电流，可根据式（2）求得节点电压Un。节点电压Un说明了谐波源节点注入电流所造成的系统节点的谐波电压大小，即产生的对系统其他节点电压的负面影响。

2.2 输电线路谐波阻抗模型

输电线路是具有均匀分布参数的元件，在潮流计算中，通常以集中参数π型等值电路来表示，如图4所示。在基波潮流计算时，等值电路参数为分布参数的简单集中。在高次谐波作用下，输电线路的分布参数特性影响更显著，在计算中采用双曲函数表示π型等值电路。参数计算可表示为［22］：

图4 输电线路谐波阻抗模型Fig.4 Harmonic impedance model of transmission line

其中，Zxn和γn分别为n次谐波下线路波阻抗和传播常数；Zln、Yln分别为π型线路等效模型的串联元件阻抗、并联元件导纳；Z0n和Y0n分别为n次谐波下输电线路的单位长度阻抗和导纳。

由图4可知，已知线路首端电流Is、电压 Us，线路采用精确模型可求得线路末端电流Im、电压Um。定义电动汽车充电站注入电网电流经过一段线路后，线路末端电流与首端电流的比值为某次谐波电流的放大倍数k，根据图4可得：

其中，Zh为输电线路第n次谐波阻抗；Yh为输电线路对地导纳；Zs为系统阻抗；ZT1、ZT2、YT分别为变压器一次阻抗、二次阻抗、励磁导纳。当考虑线路精确模型时，能够更加准确地说明电动汽车充电站产生的谐波电流对电网节点电压、线路电流的影响。

3 计算步骤

由以上分析可知，分析电动汽车充电站流入系统的谐波对电网影响的具体实施步骤如下：

a.进行初始化，建立含常规APF治理装置的电动汽车充电站模型；

b.计算各系统各节点基波电压值U1；

c.建立系统谐波导纳矩阵；

d.利用式（2）计算电动汽车站流入系统的谐波电流所产生的各节点谐波电压值；

e.获取线路谐波阻抗模型，求得谐波电流的放大倍数；

f.分析谐波源节点对系统各节点及输电线路电压、电流的影响情况。

4 算例分析

以IEEE 14节点系统为例说明电动汽车充电站所引起的各节点电压及谐波电流幅值变动情况。该系统由区域 1（13.8 kV）和区域 2（69 kV）构成，如图5所示。假设：只存在1个谐波源，该谐波源位于节点13，节点13通过Dyn降压变压器连接节点15（即电动汽车充电站节点）；电动汽车充电站连接有6组不可控整流充电机。

图5 IEEE 14节点系统Fig.5 IEEE 14-bus system

4.1 充电机对系统各节点电压的影响

6组6脉冲不可控整流充电机产生的谐波电流注入系统后，所引起的各节点谐波电压如表2所示。由表2可见：谐波电流注入节点13引起的基波电压有效值变化最为明显，达到了1.3123 kV，节点13的谐波电压有效值同样达到了最大值0.0428 kV；与节点13连接越紧密的节点，谐波电流引起的基波电压、谐波电压有效值变化越明显。此外，区域1和区域2所受到的影响显著不同，前者较为明显。

表2 系统各节点电压有效值变化情况Table 2 Variation of virtual values for different node voltages

图6为各节点各次谐波电压有效值的变化情况。电动汽车谐波电流引起的各节点谐波电压有效值变化相对较为明显的为节点 6、10、11、12、13、14，其中节点12、13、14最为显著。由图7可见，基波电流引起的各节点电压有效值变化所呈现的特征与谐波电压有效值相同，其中节点12、13、14最为显著。分析系统IEEE 14节点系统可知，由于电动汽车充电站接在节点13，在同一电压等级下，与节点13连接电气距离越近，则所引起的电压变化有效值越明显。而在区域2，电压有效值几乎未发生变化。可以得出，系统中接入谐波电源后，与谐波源电气距离最近的节点电压有效值所受冲击最大。

图7 基波电流引起的系统各节点电压有效值变化情况Fig.7 Variation of virtual value for different node voltages，induced by fundamental current

4.2 充电机对系统支路谐波电流放大倍数影响

取系统中一条13.8 kV输电线路为例进行分析。设该线路长度为20 km，单位长度电阻为0.46 Ω，单位长度电抗为0.413Ω，单位长度电纳为2.85×10-6S，电导忽略不计，利用式（3）、（4）和（7），结合 1.2 节计算结果，可求得电动汽车充电站注入系统谐波电流经输电线路后的放大值及放大倍数，如图8所示。由图8可见，虽然电动汽车充电站中不可控整流充电机所产生的谐波电流经常规APF治理后，能够满足国标中规定的注入公共连接点谐波允许值要求，并达到较好的治理效果（如表1所示，总畸变率为4.835%）［18］。但是，当考虑线路分布电容影响后，在线路末端谐波电流明显放大，放大倍数如表3所示，其总畸变率为18.22%，已不符合治理要求。由表3可见，55～75次谐波存在明显放大情况，其中71、73次谐波的放大倍数分别达到了31.633和40.237，较大的谐波电流在配电网中流动，再次经过多条线路后，可能对用户设备造成严重影响。为避免不良影响发生，需重点考虑特定次谐波或高次谐波的治理。

图8 电动汽车充电站的谐波电流注入系统前后的对比Fig.8 Harmonic currents of EV charging station，before and after flowing into power grid

表3 考虑线路分布电容影响的谐波电流值及谐波放大倍数Table 3 Harmonic current and magnification considering distributed capacitance of line

5 结论

本文研究了多组不可控整流充电机谐波大小，提出多台不可控整流充电机高次谐波监测和治理问题，并指出在考虑输电线路精确模型时，流入配电网系统的电动汽车充电站高次谐波存在谐波放大现象，给出了并网谐波电压转移程度描述方法。研究成果可为系统电流、电压准确监测提供理论基础，同时对于谐波源并网准入政策提供参考。