电力系统暂态稳定性闭环控制（四）——切机控制效果的要素分析

张保会，王怀远，杨松浩

（西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

电力系统暂态稳定性闭环控制既要充分发挥系统承受扰动的能力，又要在出现不能承受的扰动导致暂态不稳定时以最小的控制代价保持系统的稳定性，即解决闭环控制启动［1-4］的必要性和投入控制［5-9］后的有效性与经济性问题。文献［1-3］实测或预测系统运动轨迹判定大扰动后系统的暂态稳定性，对于要失去稳定的电力系统，需要施加适当的紧急控制［11］，阻止系统向不稳定发展，保持暂态稳定。

目前电力系统制定和投入紧急控制策略主要有2种方法。一种方法是大量离线计算大扰动场景，提取特征量，用特征量的组合反映暂态稳定性，对不稳定场景，通过反复试凑计算获得稳定控制方案，将其植入稳定控制系统，称为“稳控策略表”［10-11］。大扰动发生后，根据稳定控制系统实测的特征量组合，查询预植的策略表，判别是否需要执行紧急控制及选择何种控制方案，简称“离线预决策，实时匹配”。由于电力系统在逐季发展、电网方式不停变化，离线预决策需要考虑的样本量太大，且制定的控制策略难以保证在各种系统方式、运行状态下的有效性与经济性。为了适应系统的发展和减少样本的计算量，结合计算手段的进步，尝试采用另一种方法，即大量简化实际系统，根据当前的在线潮流，稳定控制中心根据给定的预想大扰动事故集，进行在线稳定性仿真计算，总结特征量及其组合的门限，制定控制启动决策表，而控制策略表难以自动详细计算匹配，可以离线计算给定几种策略，称为“在线预决策，实时匹配”［12-13］。这2种方法都是基于预想的大扰动事故集，稳定性的判别与制定的控制策略取决于实际的扰动与事故集的贴近度，并且依赖于系统模型及参数的仿真计算方法，而系统的模型（特别是负荷模型）和参数（特别是调节器响应参数）是难以精确获得的（系统在不断地发展），因此仿真结果存在可信性问题。

“响应决策，闭环控制”作为理想的紧急控制方式一直是电力研究工作者追求的目标。迄今为止，对于非线性时变电力系统的暂态稳定性离散控制，数学和控制论都没有给出有效的解决方法。基于响应的电力系统暂态稳定闭环控制，由于可使用的控制措施一般是离散、不连续的实时紧急切机、切负荷，保证控制的有效性是追求的主要目标，而控制的经济性是次要目标。文献［2-3］根据响应轨迹判别系统的稳定性，已经解决了控制启动的必要性问题，而要根据响应轨迹实时计算阻止系统不稳定所匹配的有效、经济的切机控制措施，就需要对影响控制效果的要素进行分析并加以解决，成为后续论文的内容。

本篇论文以单机无穷大系统为例，分析了切机（减出力）控制时间与控制效果之间的关系，讨论了最小切机控制的经济性与难以一次准确计算最小控制量的原因，以及在多机系统中，如何选择有效的控制地点。最后，在IEEE 39节点系统中，对控制时间、控制量大小和控制地点对阻止系统失稳的效果进行了仿真验证。

1 阻止失稳的控制措施投入越快效果越好

暂态稳定性闭环控制的目的是通过紧急控制阻止不控制就会失稳的系统向不稳定发展，而不是失稳后的再同步控制，因此其控制投入的时间一定在失去稳定之前，并且越快效果越好。为了便于理解概念，以图1的单机无穷大系统配合图2的功角特性曲线，以切机阻止系统失稳为例说明切机越快阻止失稳的效果越好。

图1 单机无穷大系统示意图Fig.1 Schematic diagram of SMIB system

图2 单机无穷大系统的等面积准则Fig.2 Equal-area criterion of SMIB system

系统的初始运行点为δ0，假定线路L2发生故障，故障切除时刻为Tc，对应的系统功角为δc；故障期间、故障切除后的电磁输出功率分别为和，稳定平衡点为δp；在故障切除时刻Tc，根据等面积定则，判出系统将要失稳，需要切机控制。

切机控制增加减速面积，在相同的控制量ΔPm1=Pm-ΔPm′下，显然在δec1（对应 Tec1时刻）切除相较于在δec2（对应Tec2时刻）切除增大了减速面积Adec2=（Pm-Pm′）（δec2-δec1），因此对于系统的稳定性而言，相同的控制量切机越早，增加的减速面积越大，阻止失稳的效果越显著。

如果追求以较小的控制代价保持系统的稳定性，则选择切机动作之后总的减速面积刚好等于加速面积。假设在Tec1时刻需要的切机量为ΔPm1=Pm-Pm′，而在Tec2时刻切机则需要增加切机量ΔPm2=Pm′-Pm″，使得 Adec3=Adec2。因此，控制时间越早，需要的控制代价就越小。

由此可以得到，相同的控制量，控制时间越早，控制效果越好；控制时间越早，所需要的控制量就越小。

对于实际的多机系统，尽管难以用等面积定则准确解释控制投入时间与控制效果的关系，按照文献［2］的等值系统［14］处理后，仍然可以用近似的等面积定则说明控制时间与控制效果的关系，并且大量的仿真结果表明，当两群失稳模式形成后，控制投入越早，阻止失稳的效果越显著。投入控制的时间与判别出系统失稳的时间和信息传输的时间有关，因此要想尽早地投入控制，离不开快速、可靠的不稳定检测、预测判据。

2 合适的控制量计算

当判别出系统失稳后，需要尽快地投入控制措施，然而所采取的控制量也必须和不稳定情景相匹配。若控制量不足，则无法通过一次控制阻止向不稳定发展，并且有可能失去最佳的控制时机；若控制量过大，会造成不必要的经济损失，甚至过控可能会引发新的稳定性问题。

根据等面积定则，当要阻止系统失去稳定时，系统的减速面积大于等于系统的加速面积，考虑经济性，取控制后的减速面积等于系统的加速面积，以此原则求得最小切机量。

加速面积可以通过故障后实时测量计算获得。而切机后的总减速面积的求取，则是一个“环锁”问题。尽管切机措施主要是切除了发电机的部分机械功率Pm和机组的惯量，但同时也使得等值发电机的暂态电抗X′d增大，导致发电机的电磁功率由下降为，如图3所示。

图3 切机前后系统功率-功角相平面图Fig.3 P-δphase planes，before and after generator shedding

切机带来发电机机械功率、电磁功率的减小，造成系统不稳定平衡点的改变，而切机后不稳定平衡点δ′u必须先要已知切机量才能准确求解，因此无法准确地求取切机后系统的总减速面积。一般而言，为了通过一次切机控制保证系统稳定，往往在假定切机后电磁功率曲线不变的前提下计算切机量，而实际执行的切机量大于计算的切机量。

对于简单系统而言，即使已知各种系统参数都难以准确计算最小切机量，只能为保证控制的有效性而略微牺牲经济性。由于实际电力系统复杂多变的性质，更难准确地计算最小控制量。但如果能够依据实测的动态响应特征，研究近似的最小控制量实时计算方法，以尽可能小的控制代价，阻止失稳，保持暂态稳定性，是具有理论和实际意义的。如果投入一次控制措施没能完全阻止失稳或后续又发生了其他扰动，系统表现出将要失稳，本系列论文所提闭环控制方案会再次启动后续控制，使得系统不会出现失稳，后续论文将对此展开详细讨论。

3 控制地点的选择

多机电力系统的失稳一般率先表现为两群失稳模式，通过切除超前群中的发电机使得超前机群与落后机群间保持稳定是本文讨论的出发点。而超前机群中包括主动超前机群和被动超前机群。主动超前机群是由受扰比较严重从而直接导致运动形态超前的发电机组成，而被动超前机群是指受主动超前机群的牵拉作用而被动超前的机群。

切除发电机一定在超前机群中选择，仿真计算表明，切除主动超前机群中的发电机可更有效阻止系统失稳，而切除被动超前机群中的发电机，不能高效阻止失稳，可能还会导致系统的稳定性恶化［15］；即使同为主动超前机群中的机组，相同的切机量切除不同的机组，产生的控制效果也不同。因此针对实时的不稳定模式，切机控制地点的选择对于保证控制效果极为重要。文献［2］基于发电机响应轨迹（功角、角速度等）已经实时辨别出超前机群和落后机群，而在超前机群中如何选择主动超前机组而非被动超前机组，避免切除某些具有切机控制负效应［8］的机组，是同时提高控制的有效性和经济性必须解决的另一个重要问题。

4 保证切机控制效果要素的验证

以IEEE 39节点系统为例进行仿真，系统接线图如图4所示。

图4 IEEE 39节点系统接线图Fig.4 Wiring diagram of IEEE 39-bus system

4.1 控制时间对控制效果的影响

故障设置为母线4和母线14之间线路在0 s时发生三相短路故障，0.21 s断开线路切除故障。功角摇摆曲线图如图5所示，超前失稳机组为发电机G31（与母线31相连发电机，其他类似）。假设切除G3180%的出力，切除时间分别为0.35 s、0.45 s和0.55 s，得到的切机后的功角摇摆曲线图如图6所示。

图5 线路4-14故障后不控制的功角曲线图Fig.5 Power angle curves when line 4-14 has uncontrolled fault

观察图 6（a）、（b）可以看出：相同的控制量，在0.35 s和0.45 s切除，系统能够保持稳定。但是在0.35 s切机后的系统最大功角差为159°，功角回摆的时刻为0.58 s，而在0.45 s切机后的系统最大功角差为168°，功角回摆的时刻为0.85 s。可以看出，相同的控制量，动作时间越早，得到的控制后摇摆角越小、回摆时间越早。

图 6（c）显示，在 0.55 s切机，因为切机太迟，切除G3180%的出力，不能阻止系统失稳。

表1列出了上述故障条件下，不同的切机时刻，保持稳定所需要切除G31的最小切机量。

从图6、表1可以看出，相同的切机量，控制时间越早，后续的角度摇摆越小；控制时间越早，保持稳定所需要的切机量就越少，当控制时间过晚时，无法阻止系统失稳。

图6 切机后的功角曲线图Fig.6 Power angle curves，with generator shedding

表1 不同切机时间对应的最小切机量Table 1 Minimum generator-shedding quantity for different shedding moments

4.2 控制量大小对控制效果的影响

故障设置为母线13和母线14之间线路0 s发生三相短路故障，0.2 s断开线路切除故障。系统的功角摇摆曲线图如图7所示，超前失稳机群为发电机 G31和 G32。

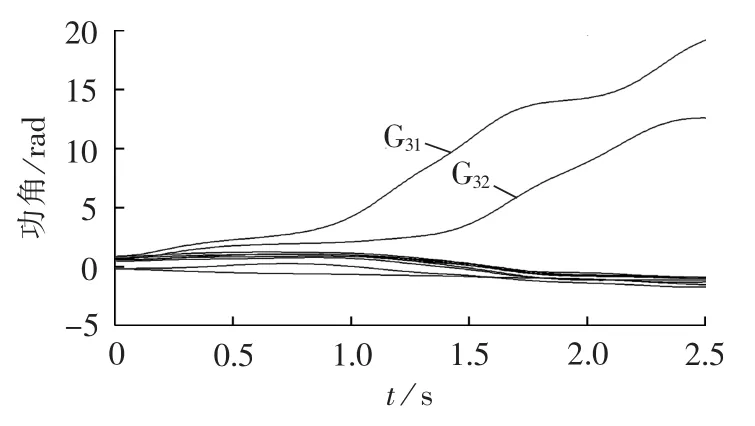
图7 线路13-14发生故障后的功角曲线图Fig.7 Power angle curves when line 13-14 has fault

假设0.45 s时切机，切机量为切除G31350 MW（40%）有功出力，摇摆曲线如图8所示，被动超前失稳机组G32已被拉入滞后群，但主动超前失稳机组G31由于切机量不足，仍然失稳。

图8 切除发电机G31350 MW的功角曲线图Fig.8 Power angle curves，with 350 MW of G31shed

假设0.45 s时切机，切机量为切除G31550 MW（60%）有功出力，摇摆曲线如图9所示，切机量合适，系统保持稳定。

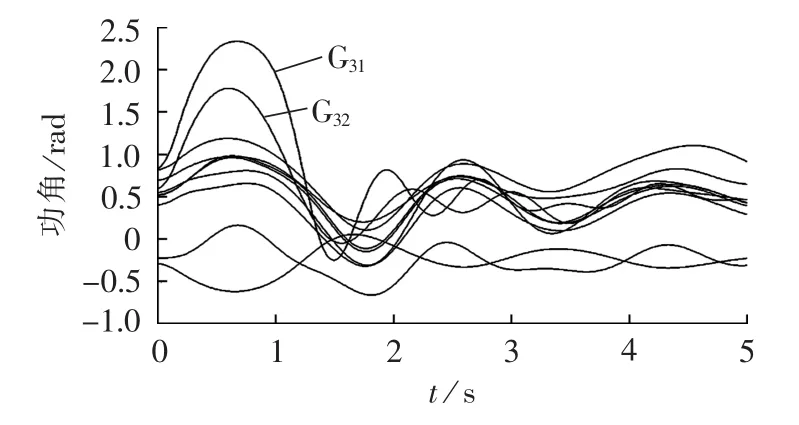
图9 切除发电机G31550 MW的功角曲线图Fig.9 Power angle curves，with 550 MW of G31shed

假设0.45 s的时候切机，切机量为切除发电机G31731 MW（80%）有功出力和发电机G32200 MW（30%）有功出力，总计931 MW有功出力。功角曲线图如图10所示，尽管系统维持稳定，但是系统因有功不足，频率持续下降，造成频率失稳，如图11所示。

图10 切除发电机G31和G32931 MW的功角曲线图Fig.10 Power angle curves，with 931 MW of G31and G32shed

图11 切除发电机G31和G32931 MW的系统频率变化图Fig.11 System frequency curve，with 931 MW of G31and G32shed

由以上仿真可以看出，控制量不足时，不能阻止系统失稳，而控制量过大时，将会引起其他的稳定性问题。

4.3 控制地点对控制效果的影响

故障设置与4.2节相同，假设0.45 s时切除被动超前失稳机组发电机G32550 MW（60%）有功出力，摇摆曲线如图12所示，主动超前失稳机组G31继续失稳，比较相同切机量、切机时刻切发电机G31后的摇摆曲线图9，说明不同的切机地点对阻止失稳的效果有极大的差别。

图12 切除发电机G32550 MW的功角曲线Fig.12 Power angle curves，with 550 MW of G32shed

故障设置与4.2节相同，假设0.45 s时切除发电机G31550 MW和发电机G32200 MW的有功出力，功角曲线如图13所示，系统仍然失稳。比较图9与图13的切机方案，尽管图13方案多切除了G32的发电量200 MW，反而将系统控制得不稳定了。可以看出，G31是有效的控制机组，而G32是具有控制负效应的机组，切机时应选择有效的控制机组，避免具有控制负效应的机组。

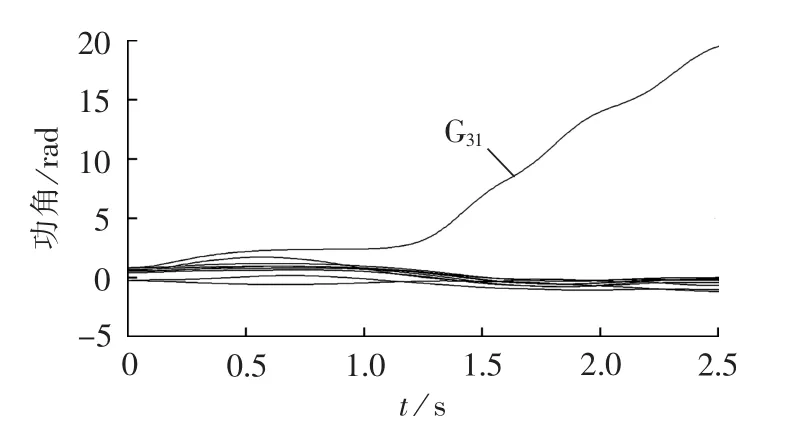
图13 切除发电机G31550 MW和发电机G32200 MW的功角曲线图Fig.13 Power angle curves，with 550 MW of G31and 200 MW of G32shed

5 结论

本文探讨了影响控制效果的3个要素：控制时间、控制量和控制地点。阻止系统失稳的紧急切机控制，切机时间越早，所需要的控制量就越小，因此需要判据能够快速准确地判别系统的稳定性；在实际的多机系统中，无法准确一次计算系统的最小控制量，需要研究依据轨迹响应的近似控制量估算方法；选择适量切除超前失稳机群中的主动失稳机组，避免切除具有控制负效应的机组。同时兼顾以上三要素，才能保证阻止系统失稳的紧急切机控制的有效性与经济性。