基于BoothCSD混合编码的模2n+1乘法器的设计

王 敏，徐祖强，邱陈辉

(江苏科技大学电子信息系，江苏镇江212003)

基于BoothCSD混合编码的模2n+1乘法器的设计

王 敏，徐祖强，邱陈辉

(江苏科技大学电子信息系，江苏镇江212003)

在余数系统的设计中，模加法器和模乘法器的设计处于核心地位，尤其是模乘法器的性能，是衡量余数系统系能的主要标志之一。文中先推导出Booth编码下的模2n+1乘法器设计的算法，然后针对Booth编码模乘法器设计中译码电路复杂的问题，提出了一种基于Booth/CSD混合编码的模乘法器设计方法，基于Booth/CSD编码的模乘法器部分积的位宽相对传统的Booth编码乘法器而言，减少了50%;经试验证明，与传统的基-Booth编码的模乘法器相比这种混合编码的模乘法器的速度提高了5%，面积减少24.7%。

电子电路设计;模2n+1乘法器;Booth/CSD编码;余数系统

近年来，随着大规模集成电路的发展，余数系统以其内在的并行特性越来越受到业内人士的重视;在图像处理、CDMA通信系统以及DSP处理器设计等领域余数系统都有较好的应用前景。在乘法器设计中，基于Booth编码的乘法器［1-3］在二进制系统中得到了广泛的应用，Booth编码的核心是通过减少乘法运算中的部分积个数来达到提高乘法器运算速度的目的，而CSD编码则是在乘数的二进制表示有较多连续的“1”时，通过某种转换，增加“0”的个数，减少“1”的个数。我们知道“0”在实际运算过程中和被乘数相乘结果为0，可看做不参加运算。文中将两种编码的优点有效结合起来，虽然CSD编码并不是每一次都能简化乘法运算，但在统计学的角度看，两者的结合可以有效的提高乘法运算速度。为表示方便，以下论文中凡出现右下角标，均表示对该值进行取模运算。

1 基于8-Booth编码的模2n+1乘法器

1.1 基8-Booth编码模2n+1乘法器结构

基8-Booth编码的模2n+1乘法器［4-6］结构图如图1所示，该结构主要包括Booth编码器、模部分积生成器、华莱士树压缩器［7］以及超前进位模2n+ 1加法器。其中华莱士树是由进位保留加法器构成，它能够对部分积进行压缩，将3个部分积压缩成2个，从而减少相加部分积的个数，其结构如图2所示。

图1 基8-Booth编码模2n+1乘法器结构

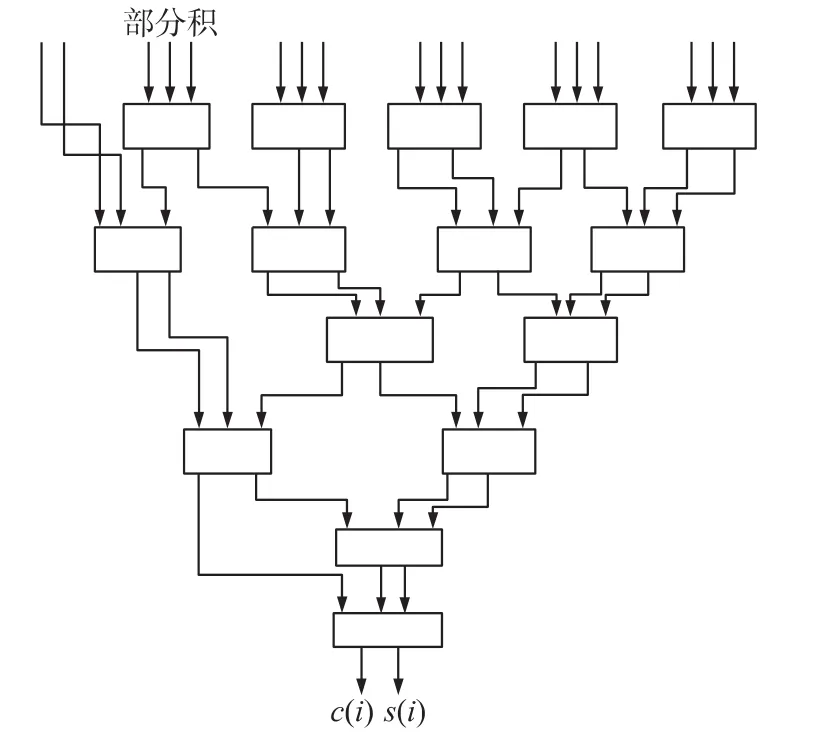
图2 华莱士树形结构

1.2 基8-Booth编码模2n+1乘法器设计算法推导

余数系统中设计模加法器和模乘法器的用意是，将乘法或加法运算的结果经过取模运算转换成较小的数，然后再用较小的数参加各类运算。比如，选定余数基为28-1，假定有两个数相乘，结果为远大于255的数，这类数参加各类算术运算时得到的结果一般也较大，但如果对其进行取模运算，取模后的结果在0～255之间，实际参加运算的操作数就小的多了，当然计算起来也更加简便。最后利用某些方法，比如中国剩余定理，将余数系统下的结果转换成人们易于接受的形式。模乘法器的设计过程中，可以先计算出乘法运算的结果，然后对该结果进行取模运算;也可以基于如下公式所提供的思路:〈x1+x2+…xk〉m=〈〈x1〉m+〈x2〉m+…，其中xi为乘法运算过程中产生的部分积，加上xi即在部分积累加前先对部分积进行一次取模运算，然后对累加的结果再次取模。由于基8-Booth运算中，每次对乘数取3位，因此首先对B进行位扩展，使其二进制表示的位宽为3的倍数，因此B可以表示成

所以对AB的乘积取模2n+1运算方法如下

为求出AB乘积取模的一般表达式，先假设一个中间变量PPi，并令

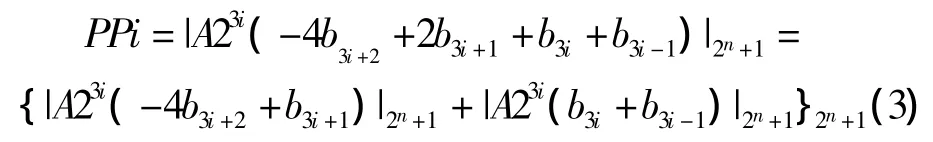
令Ei=-4b3i+2+2b3i+1，E'i=b3i+b3i-1，那么Ei的取值为{-4，-2，0，2}，E、i的取值为{0，1，2};假设Ei23i=，则

求出S1，S2，j，k的表达式如下

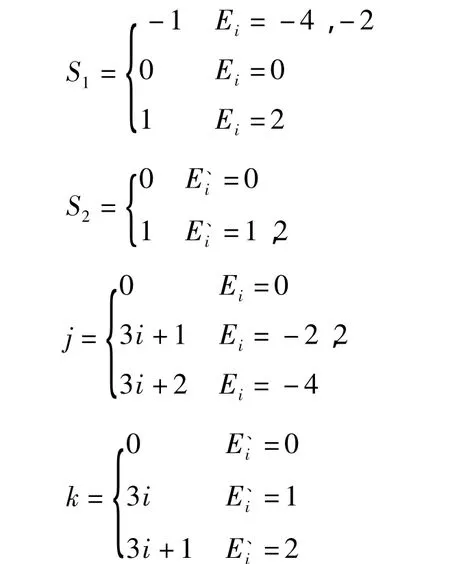
现求解|S1A2j|2n+1和|S2A2k|2n+1的值

由于

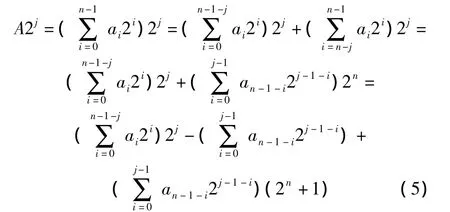
当 S1=1时，，对于无符号数m，有(m+¯m)=2j-1，¯m表示对m的二进制表示各位取反。所以-m =¯m-(2j-1)，最后得出:

当S1=0时

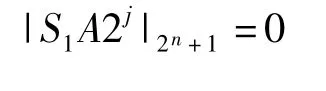
当S1=-1时

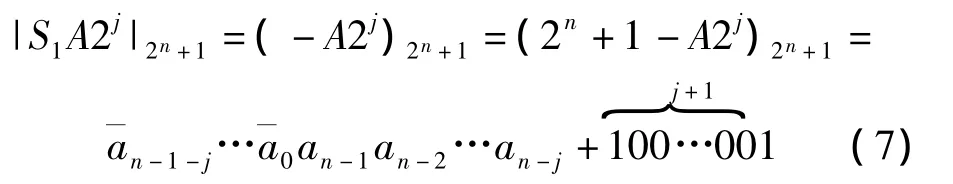
同理可求出|S2A2k|2n+1

当S2=0时

当S2=1时

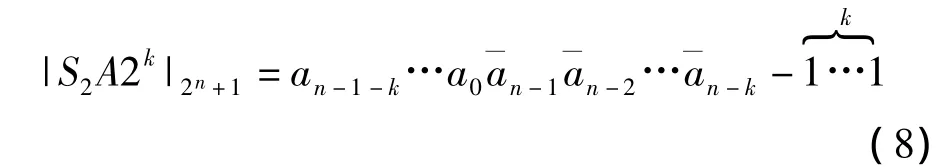
根据上面的运算结果给出基8-Booth编码的模2n+1乘法运算部分积如表1所示。

表1 基8Booth编码的模2n+1乘法运算部分积

1.3 Booth编码下模乘法器性能分析

2 基于CSD/Booth混合编码的模2n+1乘法器

2.1 CSD/Booth编码原理

采用CSD编码的优势在于:当乘数的二进制表示含有较多连续的“1”时，可以用较多的“0”代替，CSD编码［10］的内容是:从最低有效位开始，用10…取代所有的大于等于2的“1”序列.如11112= 1000CSD。基于 CSD/Booth混合编码同时结合了CSD编码可以减少乘数中“1”的个数和Booth编码可以减少部分积的特点，CSD/Booth编码的原理如下，(以8-Booth为例)假定一个数B，表示成b3k-1b3k-2…b0，将其分组，每3位为1组，即 b2b1b0，b5b4b3，…，b3k-1b3k-2b3k-3，然后将各组Booth码转换成CSD码，如111→100，011→10等，具体的CSD/Booth编码规则如表2所示。需要注意的是，在由Booth码转换成CSD码时，有时候会遇到位宽扩展的问题，如上111→100转换，就需要扩展一位，类似这种情况，采用修正的方法来得到最终的部分积和。

表2 CSD/Booth编码表

表2中之所以将3A写成4A-A，5A写成4A+ A是为了将乘法运算转换成简单的移位运算，基于CSD/Booth混合编码的模2n+1乘法器的流程图如图3所示。

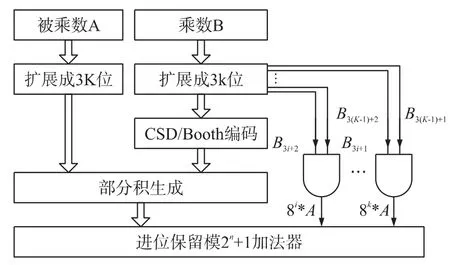
图3 模2n+1乘法器流程图

而最终对部分积之和取模运算，可以采取如下高效的方法:设A、B的二进制表示为n位，AB两数相乘的结果表示为:

其中K=(AB)/2n，U=(AB)mod 2n。

所以

而

令

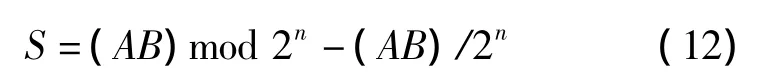
可得出

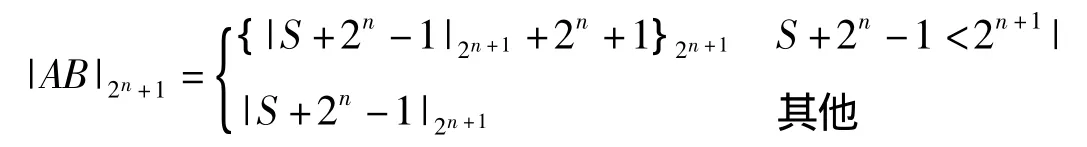
2.2 FPGA仿真验证结果及性能比较

本文以基28+1模乘法器为例验证，至于更高阶基的模乘法器的设计方法类似。采用上面的方法得到的仿真验证结果如图4，图中a、b为相乘的两个整数，result为乘积，modresult为对28+1取模运算的结果，本设计在quartus ii软件中，采用VHDL语言编写，并用ALTERA公司的cyclone ii系列FPGA芯片进行综合验证，实验表明，单纯采用基8-Booth编码的模28+1乘法器需要在更低的时钟频率下才能得到正确结果，因而在速度上，基于CSD/ Booth混合编码的模2n+1乘法器的效率要高。

图4 模28+1乘法器验证结果

两种编码方法的硬件消耗比较如表3所示。

表3 硬件资源消耗对比

3 结语

本文利用CSD/Booth混合编码的方法实现了一个模2n+1乘法器，该乘法器同时结合了CSD编码和Booth编码的优点，在取模运算的译码过程中，利用简单的截位运算替代查找表，有效的节省了硬件资源，并在一定程度上提高了模乘法器的运算速度，为更加高效的模乘法器的设计提供了良好的思路。

［1］ 汤晓慧，杨军，吴艳.基于Booth算法的32×32乘法器IP核设计［J］.电子器件，2005，28(1):231-233.

［2］ Deepal Chandel，Gagan Kumawat，Pranay Lahoty.Booth Multiplier: Ease of Multiplication［J］.International Journal of Emerging Technology and Advanced Engineering，2013，3(3):326-329.

［3］ Dina Younes，Pavel Steffan.Novel Modulo 2n+1 Subtractor and Mulitiplier［C］//The Sixth International Conference on Systems，2011:36-38.

［4］ Reto Zimmermann.Efficient VLSI Implementation of Modulo 2n±1 Addition and Multiplication［C］//Proceedings of the 14th Symposium on Computer Arithmetic，1999:51-54.

［5］ Yi-Jung C，Dyi-Rong D，Yunghsiang S H.Improved Modulo 2n+1 Multiplier for IDEA［J］.Journal of Information Science and Engineering，2007，23:907-919.

［6］ Soojin Kim，Kyeongsoon Cho.Design of High-Speed Modified Booth Multipliers Operation at GHz Ranges［R］.World Academy of Science，Engineering and Technology，2010:37-38.

［7］ 王定，余宁梅，张玉伦，等.改进型booth华莱士树的低功耗、高速并行乘法器的设计［J］.电子器件，2007，30(1):253-255.

［8］ 胡剑浩，马上.余数系统原理与在高速数字信号处理中的应用［M］.北京:科学出版社，2012:2-11.

［9］ 李磊，胡剑浩，敖思远.高速Booth编码模2n-1乘法器的设计［J］.微电子学与计算机，2011，28(11):191-193.

［10］Meyer-Baese U.数字信号处理的FPGA实现［M］.北京:清华大学出版社，2011:50-55.

［11］Marc Hunger，Daniel Marienfeld.New Self-Checking Booth Multiplier［J］.Math，Comput Sci，2008，18(3):319-328.

［12］刘东.采用Booth算法的16×16并行乘法器设计［J］.现代电子技术，2003(5):21-25.

［13］周蜿婷，李磊.基4BOOTH编码的高速32×32乘法器的设计与实现［J］.电子科技大学学报，2008，37:106-108.

王 敏(1974- )，女，汉族，重庆丰都人，江苏科技大学副教授，硕士，主要研究方向为信号与信息处理，wangmin94 @163.com。

The Design of Modulo 2n+1 Multiplier Based on Booth/CSD Hybrid Encoding

WANG Ming，XU Zuqiang，QIU Chenhui
(Department of Electronic and Information，Jiangsu University of Science and Technology，Zhenjiang Jiangsu 212003，China)

In the design of RNS system the designs of，the modulo multiplier and adder are in a core position，espically the performance of the modulo mulitipliers，which is the main mark of a successfully RNS system.In this paper，we deduce the arithmetic used in the design of the Booth-based modulo multiplier first，and then in order to solve the problem of complex decoding circuit in design，we put forward a new method，in which we bring the efficient CSD enconding technology and radix-booth encoding techniques together，the partial product of Booth/CSD encoding module multiplier has a decrease of fifty percent compared with traditional Booth based module multiplier;the test results demonstrate that，in comparision with the traditional Booth based module multiplier the speed which we take Booth/ CSD encoding method has an increase of five percent and the area has a decrease of twenty four point seven.

electronic circuit design;module 2n+1 multiplier;Booth/CSD encoding;RNS system

10.3969/j.issn.1005－9490.2014.02.044

TN710

A

1005－9490(2014)02－0373－05

2013-06-03修改日期:2013-07-16

EEACC:6120B