三相并网逆变器改进型直接功率预测控制

陈 强，任浩翰，杨志超，吕干云，章心因，叶曙光

（1.南京工程学院 电力工程学院，江苏 南京 211167；2.上海绿色环保能源有限公司，上海 200090；3.江苏金思源电力科技有限公司，江苏 南京 210018）

0 引言

随着新能源分布式发电的发展，实现新能源与电网功率转换的三相并网逆变器得到了广泛的应用与研究，其性能直接影响到并网电能质量。在众多控制方法中，直接功率控制DPC（Direct Power Control）具有控制算法简单、功率因数可调和良好的动态性能的优点[1-4]。DPC源于电机的直接转矩控制DTC（Direct Torque Control）[5]，DTC 不需要对电流进行控制，根据扇区和需求由开关表选择电压矢量，实现电机转矩和磁链的直接控制。根据同样的原理，将DPC应用到三相逆变器中，可实现三相并网逆变器有功和无功功率的瞬时功率控制[6-8]。

DPC是通过滞环控制实现功率控制，这导致运行过程中开关频率的变化，给功率电路和冷却系统设计带来很大困难，且宽频带不利于并网滤波器的设计，从而降低了并网逆变器的输出电能质量。针对以上问题，提出了采用固定开关频率DPC方案[9-10]。但传统定频直接功率控制CF-DPC（Constant Frequency DPC）通过闭环控制得到逆变器输出电压，这需要对闭环控制参数进行整定以获得良好的动静态性能，而且数字控制的延时也影响系统的性能[11-12]。针对数字控制延时、控制参数整定等难题，为进一步提高控制性能，预测控制技术被引入CF-DPC中，直接功率预测控制P-DPC（Predictive DPC）是基于数学模型实现并网功率的无差拍优化控制[10，13-14]。传统的预测控制是开环预测，针对一拍延时进行预测控制[15-16]，忽略了包括来不及更新占空比的当前采样控制周期和起作用的下个控制周期的延时[17]，很难精确预测下一拍输出量，进而影响控制精度。而且预测控制对并网电感参数比较敏感，精确实现对电感的在线辨识显得尤为重要[18-19]。

本文提出一种在同步旋转坐标系下实现的改进型P-DPC。根据控制系统实际延时两拍进行分析，首先结合电感在线辨识值对下一拍的输出功率和电流进行预估，然后得到两拍后达到目标功率所需要的输出。预测控制是基于电路参数的开环控制，预测精度和参数辨识对于控制性能至关重要，同时下一拍功率和电流预测计算复杂。为减少电感辨识误差对下一拍输出功率和电流预测精度的影响和简化预测计算，同时对电感在线辨识控制进行优化，进一步采用2倍于控制频率的采样频率，准确得到下一拍的输出功率和电流，同时采用邻域平均得到电感辨识值，提高了控制精度，然后计算得到下一个载波周期三相逆变电路的输出。利用MATLAB/Simulink构建三相并网逆变器的仿真模型进行仿真验证，并通过搭建样机进行实验研究，对控制方法进行实验验证。

1 三相并网逆变器数学模型

三相并网逆变器主功率电路拓扑如图1所示，图中，Udc为直流电源，C为直流母线电容，L为交流侧并网电感，R为线路电阻，ea、eb和ec为三相电网的相电压。

根据图1，假定三相电网对称，由基尔霍夫电压定律，在三相静止坐标系下的逆变器数学模型可表示为式（1）：

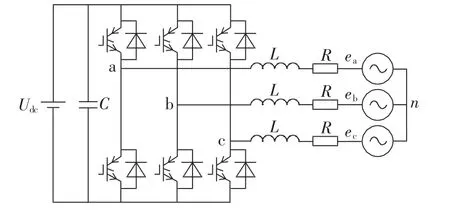
图1 三相并网逆变器电路拓扑Fig.1 Circuit topology of three-phase grid-connected inverter

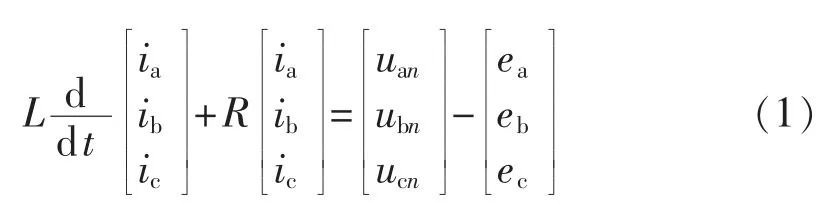
其中，uan、ubn、ucn为三相逆变器桥臂的输出端（a、b、c）相对电网中性点的输出电压；ia、ib、ic为三相并网电流。

在两相静止坐标系下进行P-DPC，电网电压αβ分量是变化的，进行预测控制时，如果不考虑这种变化将会影响系统性能，特别是在开关频率较小时。如果考虑电网电压αβ分量的变化，会增加控制算法的复杂度，而在同步旋转坐标系下，三相对称电网的d轴和q轴分量是近似不变的，所以本文的控制策略是在同步旋转坐标系下实现的。经过dq坐标变换，在两相同步旋转坐标系下的逆变器数学模型可表示为：

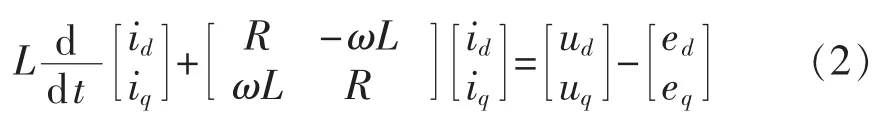
其中，id和iq为并网电流；ud和uq为逆变器桥输出电压；ed和eq为电网电压。

同步旋转坐标系和静止坐标系的夹角θ=θ1+2πf1t，f1为电网频率，θ1为起始角，θ1可以为任意值，仅需检测电网频率，这降低了控制难度。

为方便分析，通过式（3）进行耦合：

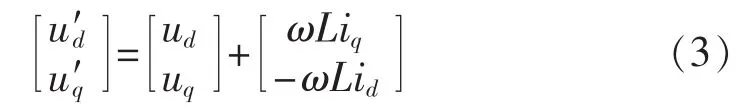
并忽略线路电阻R的影响，可得如下数学模型：

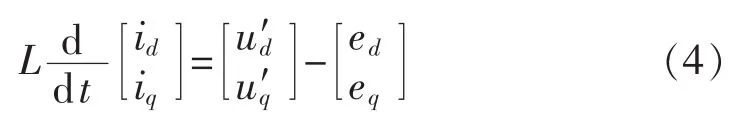
根据瞬时功率理论，在同步旋转坐标系中，三相并网逆变器输出的瞬时有功功率P和无功功率Q为：

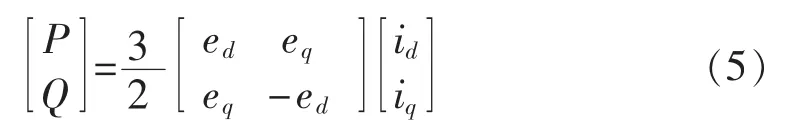
2 传统预测控制方法

本文首先分析传统预测控制方法。将式（4）离散化，可得到如下差分方程：

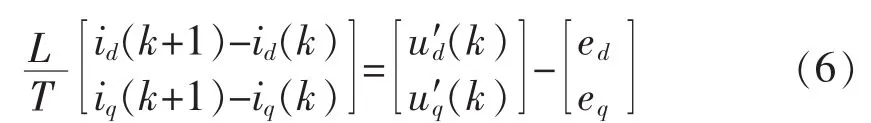
其中，id（k）、iq（k）由 kT 时刻的采样值计算得到；T 为控制周期，控制周期和三角载波周期同相同频；u′d（k）=ud（k）+ωLiq（k），u′q（k）=uq（k）-ωLid（k），ud（k）和 uq（k）为根据kT时刻采样值计算得到的控制输出量。

将式（5）离散化，并将式（6）代入，可得如下的差分方程：

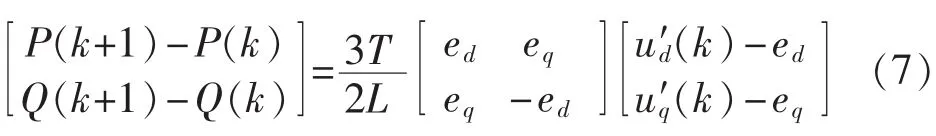
其中，P（k）、Q（k）分别为由 kT 时刻的采样值计算得到的有功和无功功率。

令 P（k+1）=Pref（k+1），Q（k+1） =Qref（k+1），Pref（k+1）为（k+1）T 时刻有功功率参考值，Qref（k+1）为（k+1）T 时刻无功功率参考值，由式（7）和式（3）可得三相逆变电路输出为：

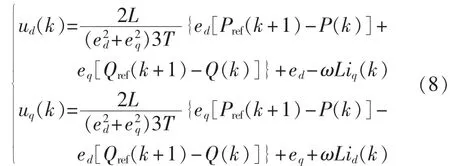
在数字控制中，需要足够的时间进行采样和控制输出量的计算，kT时刻采样并网电压和电流值，在kT~（k+1）T 时间段计算得到控制输出量，在（k+1）T~（k+2）T时间段输出。传统的预测控制显然不满足需求：ud（k）、uq（k）是对（k+1）T 时刻并网功率参考值的控制计算得到，但（k+1）T时刻并网功率其实是由ud（k-1）、uq（k-1）控制作用得到，因此（k+1）T 时刻并网功率将不能达到预期值，影响控制性能。这就需要在 kT~（k+1）T时间段预测（k+1）T时刻的并网功率和电流，实现对（k+2）T时刻并网功率的预测控制。

3 改进预测控制方法

3.1 同频采样改进预测控制方法

如图2所示，kT时刻根据采样值计算得到有功功率 P（k）和无功功率 Q（k），kT~（k+1）T 时间段的控制运算得到（k+1）T~（k+2）T 时间段三相桥输出ud（k+1）和 uq（k+1），系统的状态量在（k+2）T 时刻达到期望值，所以整个延迟时间是2T。预测控制系统如图3所示。

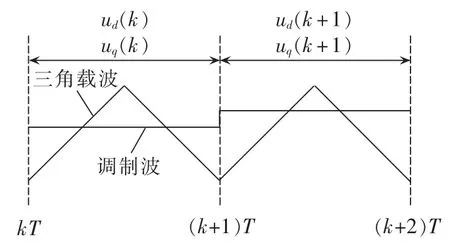
图2 三角载波和调制波关系图Fig.2 Relationship between triangular carrier wave and modulation wave

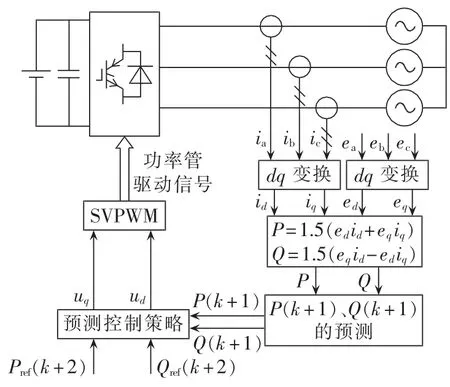
图3 三相并网逆变器P-DPC系统Fig.3 P-DPC system of three-phase grid-connected inverter

将式（4）离散化得：

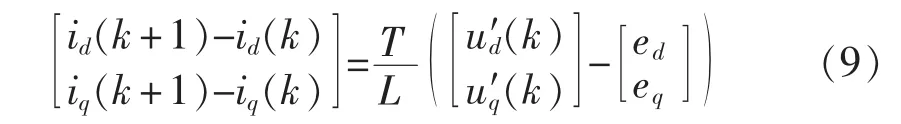
将式（5）离散化，并将式（9）代入得：

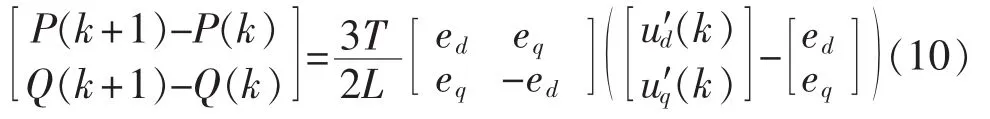
为提高对（k+1）T时刻并网功率和并网电流的预测精度，首先对电感进行辨识，由式（9）可得：

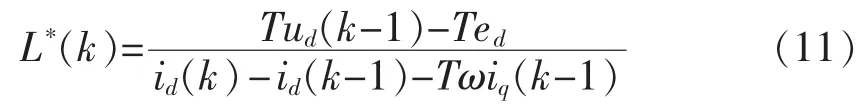
从式（11）可以看出，如单独采用d轴或q轴分量进行电感辨识，容易出现分量过小导致辨识公式中分母趋向于零而影响辨识结果的情况，故本文电感辨识采用d轴和q轴分量合成向量的模，结合式（9）和式（2）可得：

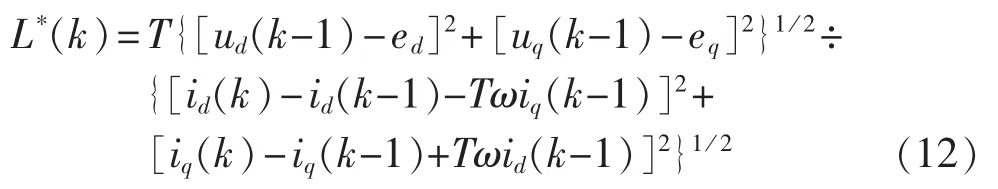
由式（10）和式（9），可得（k+1）T 时刻并网功率和并网电流预测方程为：

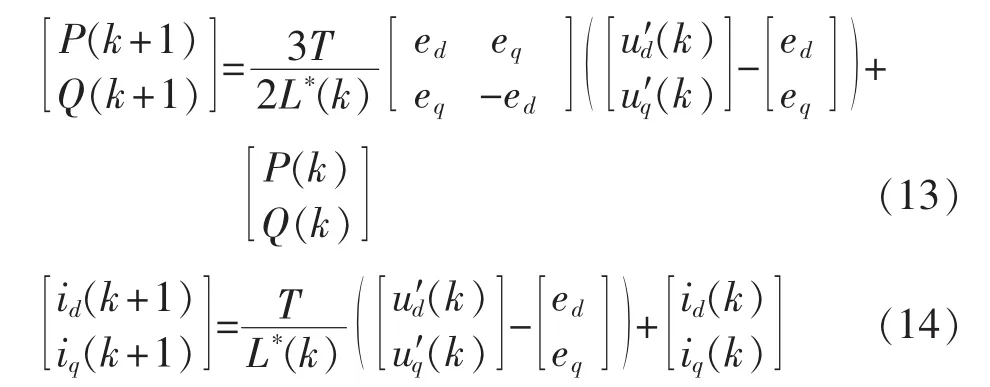
令 Pref（k+2）=P（k+2），Qref（k+2）=Q（k+2），由式（13）和式（3）可得：

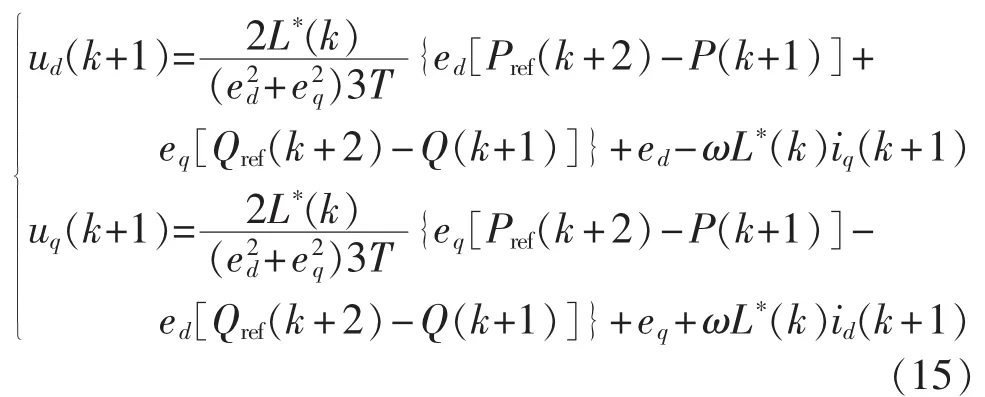
由式（13）和式（14）对（k+1）T 时刻并网功率和电流预测计算，结合式（15）可得到三相逆变电路在（k+1）T～（k+2）T 时间段输出 ud（k+1）和 uq（k+1）。

3.2 倍频采样改进预测控制方法

从以上可知，（k+1）T时刻逆变器输出电压的计算均涉及到电感辨识值 L*（k），且（k+1）T 时刻并网功率和电流预测计算复杂。为进一步提高功率的预测精度和L*（k）的辨识精度，简化预测计算，本文采用2倍于载波频率的采样频率，如图4所示，（k-1）T、（k-1/2）T、kT、（k+1/2）T、（k+1）T、（k+3/2）T 以及（k+2）T 均为采样点。

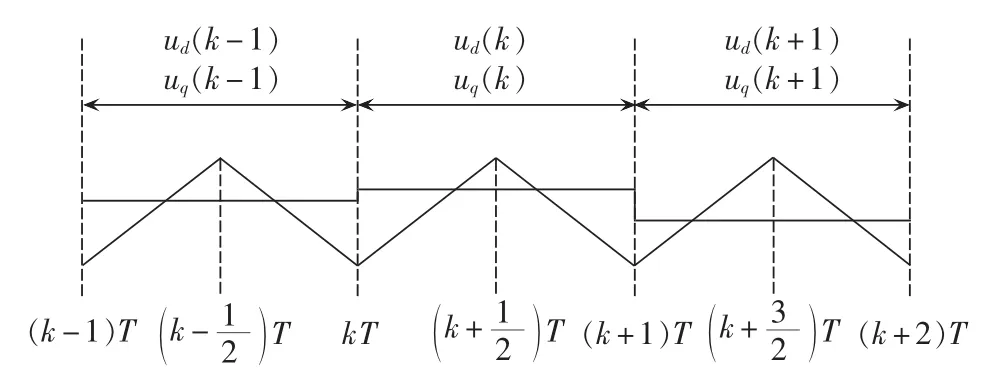
图4 采样倍频下三角载波和调制波关系图Fig.4 Relationship between triangular carrier wave and modulation wave when sampling frequency is twice control frequency

由于PWM中的三角载波为等腰三角形，因此kT～（k+1/2）T 时间段和（k+1/2）T~（k+1）T 时间段三相逆变输出电压均为 ud（k）和 uq（k）。 （k+1/2）T 时刻的有功功率 Pmid（k）和无功功率 Qmid（k）可由式（5）根据（k+1/2）T 时刻采样值计算得到。 根据式（10）可得kT~（k+1/2）T时间段的有功功率和无功功率增量与（k+1/2）T~（k+1）T 时间段的有功功率和无功功率增量相同，因此 P（k+1）和 Q（k+1）的预测公式：

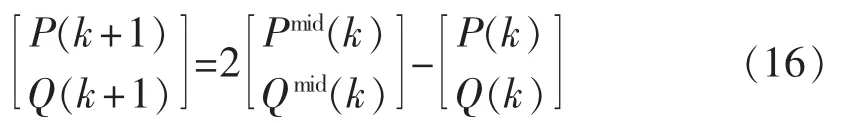
同理可得 id（k+1）和 iq（k+1）的预测公式：

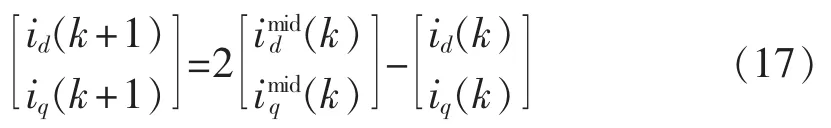
其中，idmid（k）和 iqmid（k）为（k+1/2）T 时刻的并网电流。

由式（16）和式（17）可以看出，（k+1）T 时刻的功率值和电流值可以由kT时刻和（k+1/2）T时刻的采样值准确计算得到，避免由于电感辨识值的误差影响预测精度，也极大简化了计算。

由式（12），根据（k-1/2）T~kT 时间段的逆变器输出电压和输出电流得到电感辨识值：

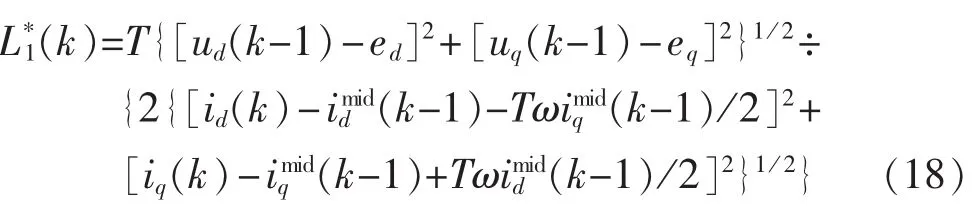
同理，根据 kT～（k+1/2）T 时间段的逆变器输出电压和输出电流得到电感辨识值：

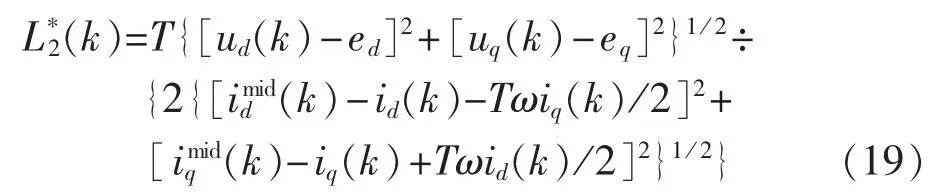
采用邻域平均得到电感辨识值：

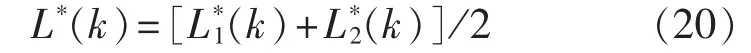
令 Pref（k+2）=P（k+2），Qref（k+2）=Q（k+2），由式（3）、式（13）、式（16）和式（17）可得三相逆变电路输出为：

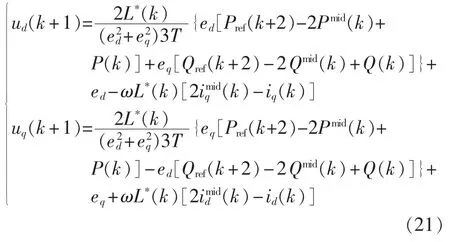
4 仿真和实验验证

利用MATLAB/Simulink搭建三相并网逆变器主电路和控制器的仿真模型对倍频采样改进预测控制方法进行验证，仿真参数为：udc=600 V，L=0.4 mH，380 V AC/50 Hz三相电网，载波频率为6 kHz。

图5为Pref=70 kW、Qref=70 kvar时，并网电流和电感辨识的仿真波形，由于电网三相对称，故选取A相的电压和电流波形。从图中可以看出，采用倍频采样改进预测控制方法的并网电流正弦度高且平稳，辨识电感值波动较小且很稳定，达到预期的控制目标。

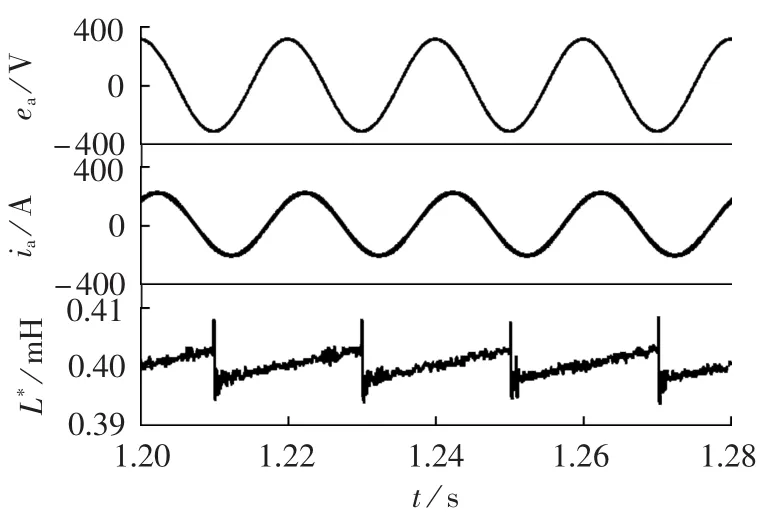
图5 并网电流和电感辨识仿真波形Fig.5 Simulative waveforms of grid-connecting current and inductance identification

图6为给定功率突变下并网电流仿真波形，有功和无功功率启动参考值分别为20 kW和50 kvar，然后有功功率跳变到70 kW，无功功率不变。从图中可以看出跳变几乎瞬间完成，并网电流平稳跳变，通过仿真可以看出功率突变下动态性能良好。

在仿真的基础上，搭建了100 kW实验样机进行实验验证倍频采样改进预测控制方法，采用英飞凌半桥模块FF600R12ME4搭建三相逆变电路，控制系统由TMS320F28335和CPLD组成，直流母线电压为550 V，变压器变比为270∶400，滤波电感为0.4 mH，开关频率为6 kHz。

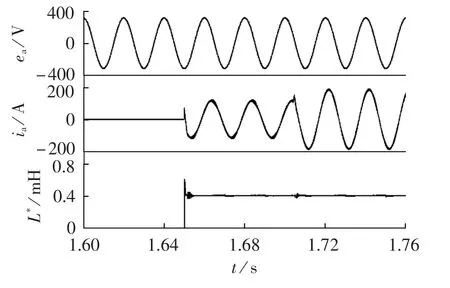
图6 给定并网功率突变下并网电流仿真波形Fig.6 Simulative waveforms of grid-connecting current for sudden change of grid-connecting power reference

图7为有功和无功功率参考值分别为70 kW和70 kvar时的并网波形。利用功率分析仪得到有功和无功功率检测值分别为69.9 kW和70.5 kvar。可以看出，实验结果验证了仿真结果，进一步验证了本文所提控制策略良好的静态性能。

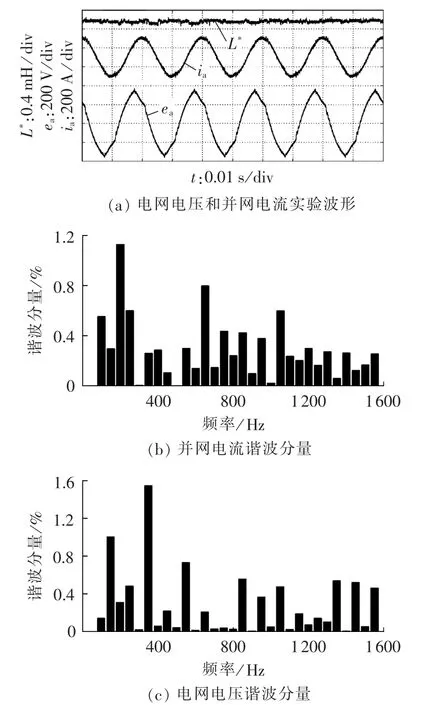
图7 有功功率和无功功率参考值分别为70 kW 和70 kvar时的实验波形Fig.7 Experimental waveforms when active power reference is 70 kW and reactive power reference is 70 kvar

图8为启动的并网电流波形，启动时有功功率和无功功率参考值分别为20 kW和50 kvar。图9为有功功率从20 kW跳变到70 kW、无功功率为50 kvar不变时的并网电流波形。从图8和图9可以看出，功率的跳变几乎是瞬间完成，过程平稳，验证了仿真结果，证明了本文所提控制策略的优良动态性能。

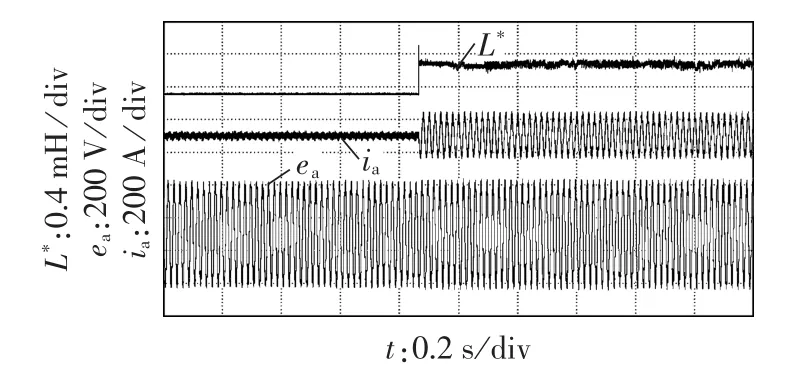
图8 启动的实验波形Fig.8 Experimental waveforms of grid-connecting current during startup

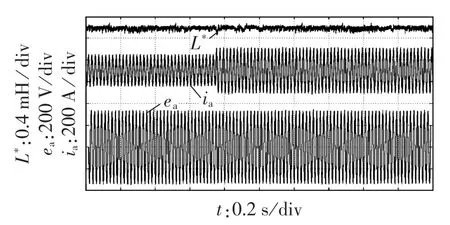
图9 有功功率从20 kW跳变到70 kW、无功功率为50 kvar不变时的实验波形Fig.9 Experimental waveforms when active power changes suddenly from 20 kW to 70 kW and reactive power keeps 50 kvar

5 结论

本文对三相并网逆变器的P-DPC进行了分析和改进，提出了一种改进型P-DPC，在同步旋转坐标系下实现。提出了采用2倍于载波频率的采样频率，不需要复杂计算，就能准确计算得到下一拍的并网功率和电流值，同时采用领域平均得到较好的电感辨识结果，并将预测值和辨识值应用于无差拍并网功率预测控制。利用MATLAB/Simulink搭建仿真模型进行验证，用样机进了实验验证，仿真和实验结果显示本文所提方法具有良好的动静态性能。