无线传感器网络中多Sink节点位置部署研究*
韩凯州, 马福昌
(1.太原理工大学 新型传感器与智能控制教育部重点实验室,山西 太原 030024;2.太原理工大学 测控技术研究所,山西 太原 030024)
0 引 言
无线传感器网络(WSNs),即通过WiFi,Zig Bee等无线方式[1],使大量的传感器节点相互联系、处理、传输信息的网络。在实际应用中,无线传感器网络中可能包含一些异构节点,与普通的同构节点相比,这些异构节点除了处理能力更强,计算能力、存储空间更具优势以外,也消耗更多的能量。然而在整个网络中安排适量的异构节点又可以提高整体网络的数据传输能力,从这个角度分析可以延长网络寿命。因此,异构节点在网络中对整个网络的能量消耗和网络寿命有很大的影响,亦即网络寿命取决于关键节点的寿命。
在许多文献中都有对异构节点位置部署的研究,这些研究针对不同的模型,提出了例如:Global算法[2]、lhop迭代算法、GEP-MSN算法等[3]。本文将针对非均匀分布的无线传感器网络,就异构节点的位置部署问题进行研究分析,利用区域密度优先(RDF)算法进行分析,提出一种方便高效的异构节点位置部署的算法[4,5]。
1 网络能耗与节点密度的分析
1.1 非均匀分布的节点分布与能耗的关系
在非均匀分布的无线传感器网络中,由于传感器节点随机的分布,呈不均匀状态,每个节点所消耗的能量也是不均匀的[6]。Perillo等人根据节点传输数据的方式提出2种情况:一种是传感器节点采用多跳方式向Sink节点传输数据,此时离Sink节点较近的节点除需要传送自己的数据外,还需要转发其他节点的数据给Sink节点,因此,会消耗更多能量而先于其他节点死亡;另一种是传感器节点采用单跳方式向Sink节点传送数据,此时每个节点都只负责发送自己的数据给Sink节点,因此,离Sink节点远的节点会消耗更多能量而先于其他节点死亡。因此,给定一个非均匀分布的无线传感器网络,且该网络采用的发送方式是多跳,很显然,在此网络中部署Sink节点时,应当把Sink节点部署在传感器节点密度大的地方(图1)。
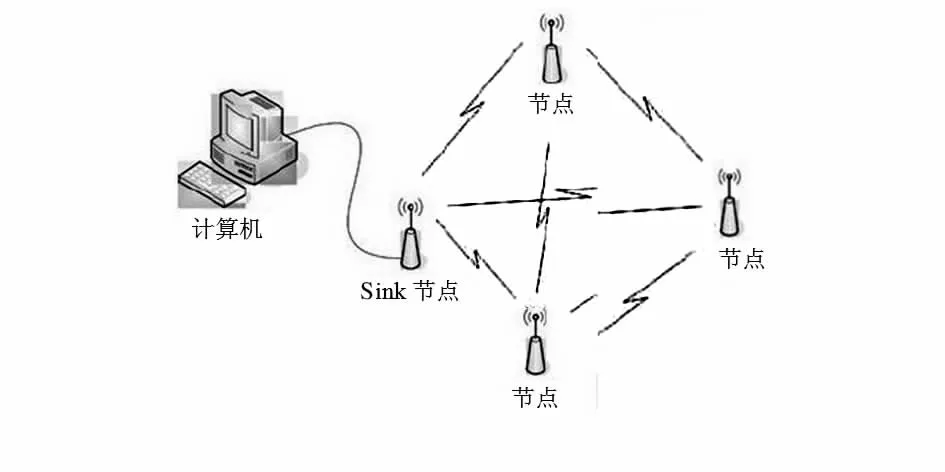
图1 无线传感器网络模型
1.2 均匀分布的网络中节点的能耗
根据文献知道,传感器节点最主要的能耗分为感知数据、发送数据和接收数据所消耗的能量三部分,即
(1)
其中,f为单个传感器节点的数据产生速率;β1,β2分别为发射电路和放大电路的能耗;r为2个节点之间传输距离;n为路径损耗系数(r小于阈值时,n=2;r大于阈值时,n=4)。
在节点均匀分布的无线传感器网络中,所有的节点都均匀分布在该网络里。假定这样一种情况,网络分布在半径为R的圆形区域,Sink节点在圆心,传感器节点密度为ρ1,传输半径为rc,每个周期传输的数据量为f,可得出每个节点能量负载如下:
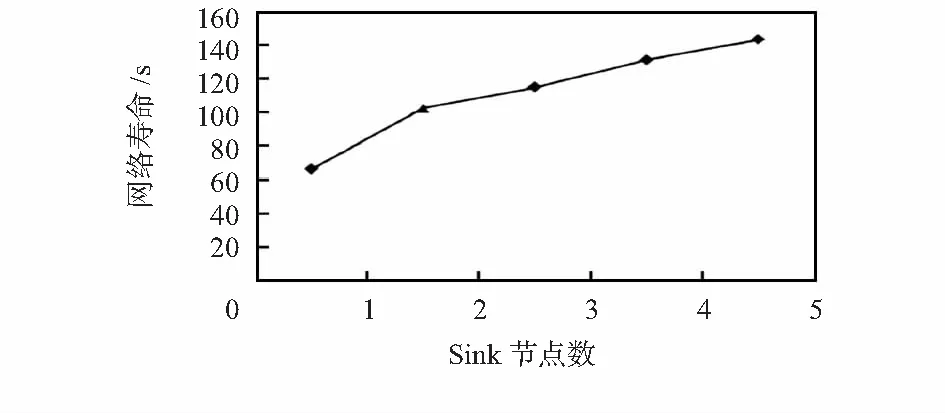
1)当rc (2) 2)当rc≥d0,n=4时,能量消耗为 (3) 在节点非均匀分布的无线传感器网络中,先考虑一种简单情况。假设该网络中Sink节点数为1,在距离该Sink节点lm的范围内,普通节点的密度为ρ,且每个传感器节点的能量消耗是均衡的,那么,该网络应满足如下公式 (4) 假设在非均匀分布的网络区域中,区域为x=R的圆形区域,传感器密度为ρ1,结合式(2)、式(3),有如下结论: 1)rc (5) 2)rc≥d0时,得式(6) (6) 由以上公式可以得出如下结论:当x(传感器节点到Sink节点的距离)越大时,节点的密度ρ就越小,换句话说,如果每个节点的能耗是相同的,那么,在离Sink节点越远的地方传感器节点的分布就越不密集。 大部分关于无线传感器网络中异构节点部署的算法[7],比如递归算法等,它们的基本思路都是把Sink节点放置于传感器节点分布集中的地方,但这些算法大都较为复杂,不利于实现。这里提出的RDF算法,依然沿用上述思路,但相对较为便捷,更利于实现。 如图2所示,假设传感器非均匀的分布在一个矩形区域里,将这个区域用直角坐标系将其划分为4个象限,并用小栅格对每个区域进行划分,用n1表示栅格的数目。与此同时,每个Sink节点的传输范围用半径为r的圆盘表示。此外假设每个象限中Sink节点的数量为n2,每个Sink节点传输范围里面的节点数量为n3。 图2 传感器网络象限栅格分割图 RDF算法具体可以描述为: 1)所有的栅格都是未标记的; 2)对每一个栅格按顺序扫描,把Sink节点依次部署于每一个栅格的中心,记录每一次落入Sink节点覆盖范围中传感器节点的数量; 3)扫描结束后,如果其中一个栅格的节点数量大于其他所有栅格中的节点数量,那么,此栅格为最优栅格; 4)如果有多个栅格的节点数量相同且大于其他所有栅格中的节点数量,那么,考虑2种情况: a.这些栅格处于同一象限,则其中任一栅格为最优栅格; b.这些栅格处于不同象限,则部署最少Sink节点的那个象限所对应的栅格就是最优栅格。 从前面的叙述中知道,关键节点的寿命决定无线传感器网络的寿命,关键节点就是落在Sink节点通信范围内的传感器节点[8]。当网络里存在多个Sink节点时,要求这些关键节点可以平均地承担普通节点的数据传送功能。由2.1节的结论可以知道,RDF算法通过选取最优栅格,较好地解决了这个问题。 由文献知道,一个确定异构节点位置的无线传感器网络的寿命可以表示为 (7) 给上式中的参数选取一定的数值,图3显示的就是当网络中部署了1~5个Sink节点时网络寿命的时间。 图3 网络寿命 为了综合分析和验证本文本文中描述的RDF算法,对RDF算法、递归算法以及随机分布3种情况的网络寿命和报文的递交概率在Matlab上进行了多次仿真,证明了RDF算法在这两方面都更具优势。 假设100个传感器节点随机分布在1 000 m×1 000 m的矩形区域里面,Ei=100 J,εt=0.015 J,εr=0.015 J,εt=0.5 J。Sink节点数量为1~9。 3.2.1 不同部署算法网络寿命的比较 如图4所示,RDF算法和递归算法下部署的Sink节点的网络,其寿命基本接近,随机分布的寿命则小于二者,说明RDF算法在延长网络寿命方面作用明显,且比递归算法更简单方便利于实现。 图4 不同部署策略下网络寿命 3.2.2 不同部署算法报文的递交概率的比较 报文递交概率是对网络寿命检测的一项主要指标,如图5所示,RDF算法和递归算法的保温递交概率更高于随机分布的情况,而RDF算法相对更简单便捷利于实现。 图5 不同部署策略下报文递交概率的比较 本文在分析了随机分布的无线传感器网络能耗和节点密度的关系,在此基础上提出了RDF算法,该算法以优化传感器网络中的Sink节点的部署来达到降低能耗的目标。通过仿真实验证明:RDF算法在重新恢复连通度时比递归算法的连通度高且异构节点放置位置优越。虽然在网络寿命上RDF算法和递归算法相接近,但是,RDF算法更适合实际应用。因此,RDF算法是一种简便可行的算法。 参考文献: [1] 王永杰,杨小平.基于无线传感器网络的智能小区监控系统设计[J].制造业自动化,2011,33(1):68-70. [2] Dai S,Tang C,Qiao S,et al.Optimal multiple sink nodes deployment in wireless sensor networks based on gene expression programming[C]∥The Second International Conference on Communication Software and Networks,ICCSN’10:IEEE,2010:355-359. [3] Vincze Z,Vida R,Vidacs A.Deploying multiple sinks in multi-hop wireless sensor networks[C]∥IEEE International Conference on Pervasive Services,IEEE,2007:55-63. [4] Gu Y,Wu Q,Cai X,et al.On efficient deployment of high-end sensors in large-scale heterogeneous WSNs[C]∥ IEEE 6th International Conference on Mobile Ad Hoc and Sensor Systems,MASS’09,IEEE,2009:912-917. [5] Friedmann L,Boukhatem L.Efficient multi-sink relocation in wireless sensor networks[C]∥Third IEEE International Confe-rence on Networking and Services(ICNS),2007:90. [6] 张萃玲,陈志刚,刘安丰,等.非均匀部署 WSN 的能量空洞避免策略[J].计算机工程,2010,36(2):83-86. [7] Wang Q,Xu K,Takahara G,et al.Device placement for heterogeneous wireless sensor networks:Minimum cost with lifetime constraints[J].IEEE Transactions on Wireless Communications,2007,6(7):2444-2453. [8] Xu K,Wang Q,Hassanein H,et al.Optimal wireless sensor networks (WSNs) deployment:Minimum cost with lifetime constraint[C]∥IEEE International Conference on Wireless and Mobile Computing,Networking and Communications,(WiMob’2005),2005:454-461.1.3 非均匀分布的节点的能耗
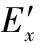
2 RDF算法的原理和应用
2.1 RDF算法的提出和原理

2.2 RDF算法分析
3 算法仿真
3.1 场景设计
3.2 仿真结果


4 结束语

