基于最小误差平方和的无线传感器网络多边定位算法
周海洋, 余 剑, 张卫涛
(1.电子工程学院 电子线路教研室,安徽 合肥 230037;2.解放军 63758部队,福建 厦门 361021)
0 引 言
在无线传感器网络的各研究分支中,节点定位是无线传感器网络中的重要技术。 目前无线传感器网络节点定位方法主要分为两类:基于测距的(range-based)方法和非基于测距的(range-free)方法[1],基于测距的方法需要测量节点间的距离或者角度信息,然后使用三边测量、三角测量或者多边定位算法[2]实现节点间的定位。目前常见的测距技术包括:接收信号强度指示(received signal strength indication,RSSI)法[3]、到达角(angle of arrival,AOA)法[4]、到达时间(time of arrival,TOA)法[5]和到达时间差(time difference of arrival,TDOA)法[6]。
本文主要研究的是基于RSSI的定位算法。这种方法是通过测出接收信号的场强值和已知的信道衰落模型及发射信号的场强值估算出收发信机节点之间的距离,根据多个距离值即能估计出目标的位置。一般情况下,如果同时有3个参考发信机节点,就可以确定收信机节点的位置了。基于RSSI的定位方法克服了TOA,TDOA和AOA方法需要额外的硬件设备的缺点,实现起来比较简单。它首先需要确定待测环境下的信号传播模型的各个参数,然后便可根据定位目标接收到的来自参考点的接收信号强度计算出定位目标与参考点之间的距离,进而利用几何法计算出定位目标的位置。多边定位算法是几何法中比较常用的一种算法,通过多个参考节点与定位节点之间的距离构建方程,通过最小二乘法求解,具有较高的定位精度,但是多边法也存在不足之处,构建方程过程中参考节点序号的选取会对定位精度产生一定影响。本文通过对测距误差平方和的分析,选取合适的参考节点序号,有效地提高了定位精度。
1 基于RSSI的多边定位算法原理
如图1所示,已知参考节点A1,A2,A3,A4…的坐标为(x1,y1),(x2,y2),(x3,y3),(x4,y4) …。设位置未知节点(盲节点)A0坐标为(x0,y0),参考节点与盲节点之间的测距距离为d1,d2,d3,d4…。设盲节点的位置估计值为(x,y),参考节点到估计位置的距离与测距之间的差异用式(1)表示
i=1,2,3,…n.
(1)
误差平方和记为
(2)
目前的常用的方法是通过最小二乘法来获取最优的位置估计[7],具体过程如下:
首先对公式(2)处理得
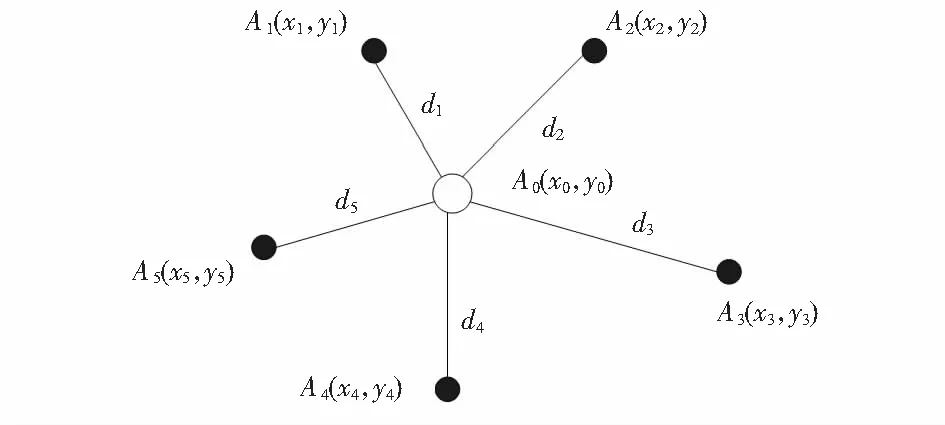
图1 多边定位算法原理图

(3)
然后将第1个至第n-1个方程分别减去第n个方程(此处选取的是第n个方程作为消元中的被减方程),整理后可得
(4)
写成线性方程的形式AX=B,
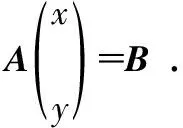
(5)
其中
可得出最小二乘解
(6)
2 多边定位算法分析
文献[8]指出了多边定位算法的一个不足:当某盲节点的参考节点数n>3时,基于式(6)得到估计位置会受到参考节点标号的影响,即对固定的n个邻近节点,参考节点不同的标号使得消元过程中被减的参考方程不同,导致估计结果不同。
文献[8]对这一现象进行了分析,认为原因是利用消元法由式(1)得到了式(5),解式(6)是式(5)最小二乘解,但一般不是最小化估计均方误差平方和(式(2))的最优估计值。这一现象对最后的定位精度也会有影响。
3 算法的提出

4 实验结果与分析
本文研究的是以RSSI测距为基础的多边定位算法,实验使用TI公司的无线收发芯片CC2430完成固定节点和待定节点间的通信以及RSSI的采集。CC2430有一个内置的RSSI,其数字值为8位有符号的二进制补码,可以从寄存器位RSSIL.RSSI_VAL读出。
在基于RSSI测距实验中,信号衰减模型一般简化为
RSSI=-(10nlgd+A),
(7)
式中n为信号衰减因子,范围一般为2-5;d为定位节点与参考节点之间的距离,单位为m;A为定位节点与参考节点之间的距离,d为1 m时测得的信号功率。实验中,测得n为3.5,A为40 dBm。
实验场景是选择在学校操场的空旷区域,区域大小为15 m×15 m,4个参考节点放置在正方形区域的4个角落。如图2所示。
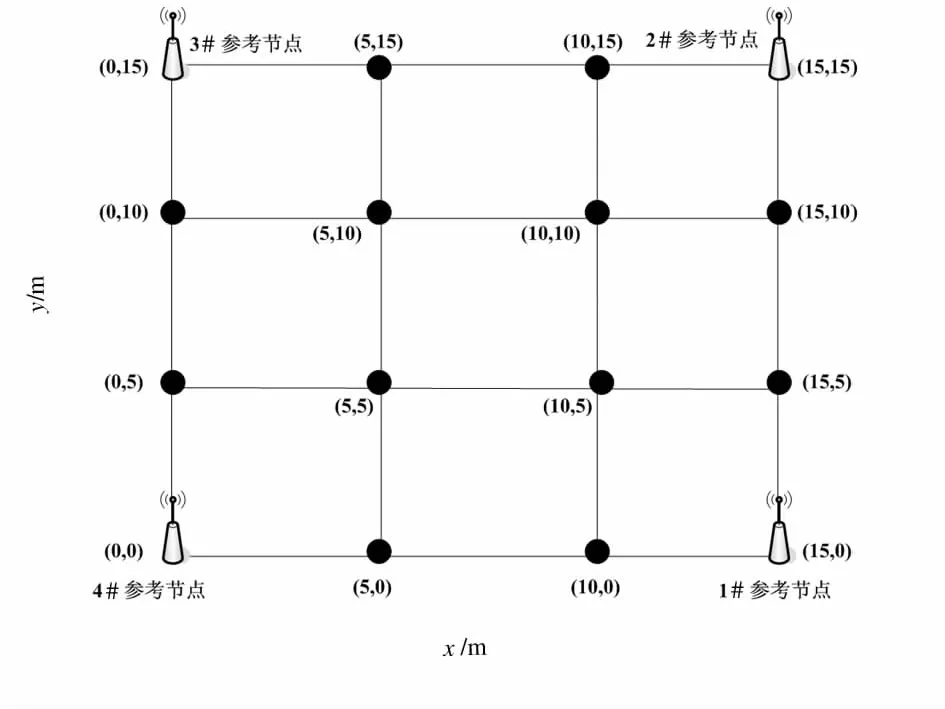
图2 实验场景(15 m×15 m)
实验结果以(5,5)m,(5,10)m,(10,5)m,(10,10)m为例,分别分析了4个参考节点分别作为消元对象时所产生的误差平方和值和定位精度,本文选取测试坐标和实际坐标之间的欧氏距离作为定位精度量值。以盲节点实际位置为(5,5)m为例,从图3可以看到当4#参考节点作为消元过程对象时,误差平方和最小,此时对应定位精度也最高。图4、图5、图6同样显示了误差平方和最小的对应的参考节点作为消元对象时,定位精度是最高的。
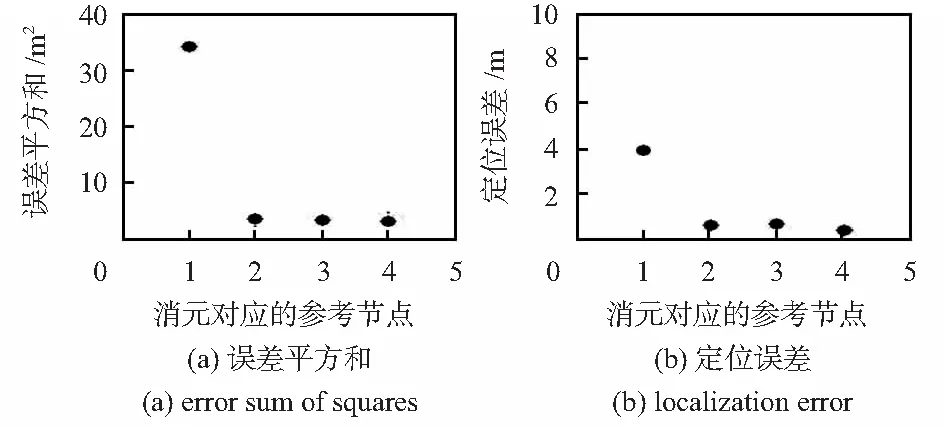
图3 盲节点位于(5,5)m误差平方和和定位误差

图4 盲节点位于(5,10)m误差平方和和定位误差

图5 盲节点位于(10,5)m误差平方和和定位误差

图6 盲节点位于(10,10)m误差平方和和定位误差
如表1,不同的参考节点作为消元对象会产生不同的定位误差。最大的定位误差3~4 m左右,而最小误差平方和对应的参考节点作为消元对象所产生的的定位精度明显提高,以本文实验的4个定位位置为例,最大定位精度可达到3.6 m。

表1 定位精度对比表
5 结 论
本文在结合文献分析多边定位算法基础上,提出了基于最小误差平方和的多边对位算法,根据不同参考节点作为消元对象产生的误差平方和,选取合适的参考节点作为消元对象,这种方法对于提高定位精度有较好的效果。以实验中的参考位置为例,定位精度最大可提高3.6 m。但是该方法性能的提高是以牺牲计算复杂度为代价实现的,因此,这种更适合对于计算复杂度要求不高的定位场景。
参考文献:
[1] Mao Guoqiang,Fidan B,Anderson B D O.Wireless sensor networks localization techniques[J].Computer Networks,2007,51(10):2529-2553.
[2] 王 琦.基于无线传感器网络的室内定位技术研究与实现[D].西安:西安电子科技大学,2012:11-15.
[3] 章坚武,张 璐.基于Zig Bee的RSSI测距研究[J].传感技术学报,2009,22(2):285-288.
[4] Patwari N,Hero A O,Perkins M,et a1.Relative location estimation in wireless sensor networks[J].IEEE Tansactions on Signal Processing,2003,51(8):2137-2148.
[5] Priyanath N B,Chakraborty A,Balakrishna H.The cricket location support system[C]∥Proceeding of Mobile Computing and Networking,Boston,ACM,2000:32-43.
[6] Niculescu D,Nath B.Ad Hoc positioning system(APS)using AOA[C]∥Proceeding of the IEEE/INFOCOM’2003:IEEE Computer Society,2003:1734-1743.
[7] Savvides A,Han C C,Srivastava M.Dynamic fine-grained localization in Ad Hoc networks of sensors[C]∥Proceedings of Mobile Computing and Networking,Rome:ACM,2001:166-179.
[8] 罗 旭,柴 利,杨 军.无线传感器网络SL-n迭代定位算法[J].通信学报,2011,32(5):130-138.

