适用于带并联电抗器输电线路的电流模型识别纵联保护新原理

申全宇，宋国兵，索南加乐，马 超

（西安交通大学 电气工程学院，陕西 西安 710049）

0 引言

分布电容一直是制约超高压保护可靠性和灵敏性的主要因素[1-2]，随着我国特高压电网的发展和远距离大容量输电线路的出现，该问题更加突出。针对这个问题，继电保护工作者提出了许多解决方案，主要分为电容电流补偿法和不受分布电容影响的保护新原理2类，它们在实际中都存在一定缺陷[3]。

目前由于电压信号易受干扰，而电流信号不太容易受到干扰，同时为了使超高压保护能够快速动作，需要准确地提取暂态故障信息。因此研究基于暂态故障电流的新型保护原理成为一种可行的方法。该原理的关键技术在于故障电流信号频谱的分析算法。

最小二乘矩阵束算法[4-9]是一种性能优越的现代信号处理方法，它以衰减指数和作为信号模型，可以精确快速地计算出故障电流的特征信息，包括频率分布、幅值、衰减因子和初相角等信息。矩阵束算法优良的频谱分析能力使得基于暂态信息保护新原理的实现成为可能。

文献[3]利用双端故障电流的暂态信息，很好地解决了超高压线路分布电容对保护的影响，但其没有考虑并联电抗器。并联电抗器可以有效地防止过电压，补偿分布电容电流，消除单相重合闸潜供电流的影响，在超高压及以上电压等级线路中广泛使用。因此，研究适用于带并联电抗器的电流模型识别保护新原理，对电流模型识别原理在实际中的应用具有重大意义。

本文针对两端带并联电抗器的输电线路，提出了一种基于电流模型识别的纵联保护新原理。首先在复频域故障附加网络下分析两端带并联电抗器输电线路的故障特征，建立相应的故障特征模型，接着构造模型误差函数描述实际故障数据与特征模型的符合程度，提出基于模型识别的保护判据。该保护新原理考虑输电线路带并联电抗器的情况，无需补偿电容电流，从根本上消除了分布电容的影响；充分利用故障电流信息，不引入电压量；采用10 ms的短数据窗，动作灵敏快速。以ATP仿真和动模仿真验证新原理的有效性。

1 矩阵束算法简介

设故障电流可以表示成如下M个指数函数的线性组合，采样后的离散表达式为：

其中，yk为实际观测到的电流信号第k个采样值；Rj为第j个谐波信号的复幅值；αj和ωj分别为第j个谐波信号的衰减因子和振荡角频率；SN（k）为噪声；为采样时间间隔；k=0，1，…，N-1，且N为最大采样点数。

其中，L为矩阵束参数，恰当地选择L可以抑制噪声的影响。通常，L在N/3～N/2之间取值。

由矩阵束原理可知，zj恰好就是Y2-λY1的广义特征值，也即矩阵G=Y1+Y2的特征值，其中，Y1+为Y1的Moore-Penrose伪逆矩阵。

求解出矩阵G的特征值zj，即可给出信号的特征频率和衰减因子：

由式（5）所示的线性方程组，利用最小二乘法给出 Rj（j=1，2，…，M）的值。

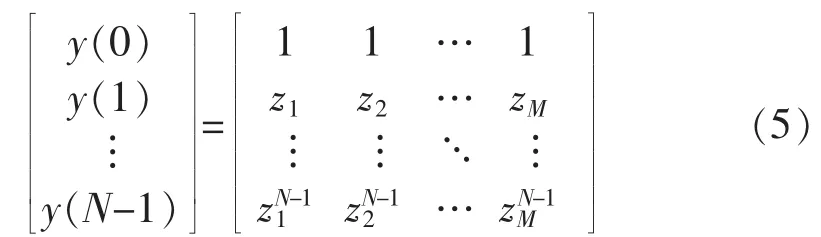
在已知zj和Rj后，故障电流各频点角频率ωj、衰减因子 αj、幅值 Aj、初相位 θj可由式（6）给出。

其中，j=1，2，…，M。

2 两端带并联电抗器的线路故障特征分析

以单相电路为例，在故障附加网络下，由复频域分别推导出区外故障和区内故障时，线路两端母线侧故障电流和差比值的理论表达式。

2.1 n侧区外故障特征模型

n侧区外故障时，考虑过渡电阻的故障附加网络如图1所示。

图1 n侧区外故障附加网络图Fig.1 Fault component network of out-zone fault at n side

超、特高压线路的电阻和电导均较小，可以近似忽略不计，线路两端母线电压以及线路上故障电流应满足线路分布参数方程[10]：

其中，Zc0为线路波阻抗，为线路单位长度的电感值和电容值；，为传播系数；d为线路长度；s为故障电流各个频点的复频率。

此外，m 侧故障电压、电流满足式（8）、（9）：

n侧故障电流满足等式：

其中，Zm为m侧系统阻抗；l1为m侧并联电抗器的电感值；l2为n侧并联电抗器的电感值。联立式（7）—（10），可以得到：

进一步可以得到线路两端互感器电流故障分量和差比值表达式为：

当已知线路参数l0、c0、d和两端并联电抗器电感值 l1、l2时，两端互感器故障电流和差比值 Hn（s）只与故障电流各个频点复频率以及m侧系统阻抗Zm有关，而与过渡电阻等其他因素无关，该表达式反映了n侧区外故障特征，可以作为n侧区外故障的特征模型。

2.2 m侧区外故障特征模型

m侧区外故障时，线路两端母线侧故障电流和差比值理论表达式推导过程与n侧区外故障时相类似，推导结果为：

其中，Zn为n侧系统阻抗。

同样，当已知输电线路参数和两端并联电抗器参数时，两端母线侧故障电流和差比值只与故障电流各频点复频率以及n侧系统阻抗有关，与过渡电阻等其他因素无关。该表达式反映了m侧区外故障特征，可以作为m侧区外故障特征模型。

2.3 区内故障特征模型

发生区内故障时，考虑故障点过渡电阻的故障附加网络如图2所示。

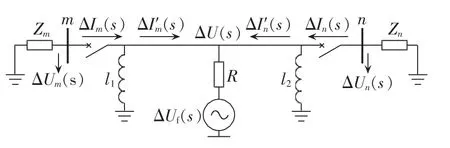
图2 区内故障附加网络图Fig.2 Fault component network of in-zone fault

对输电线路，采用与区外故障相似的推导方法，可以得到：

其中，p为故障点到m侧母线距离与输电线路全长的比值，0＜p＜1。

进一步可以得到两端母线侧故障电流和差比的理论表达式为：

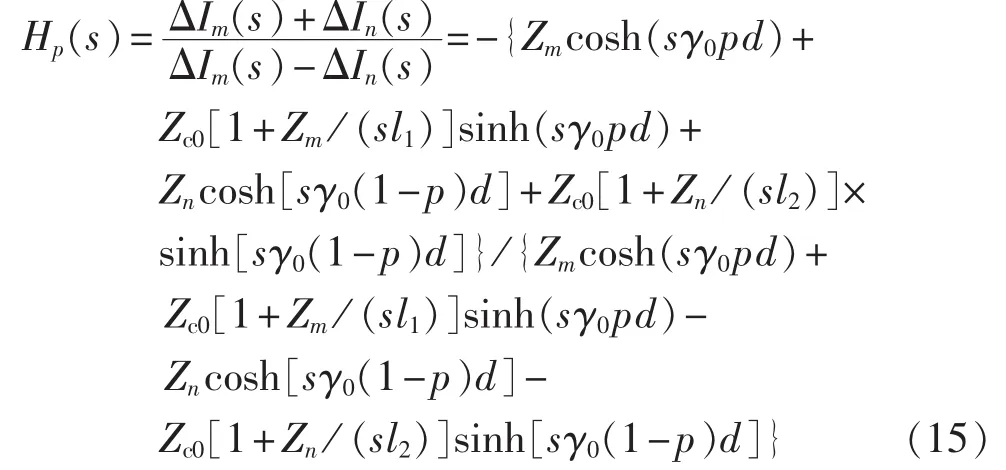
可以看出，当已知线路参数和两端并联电抗器参数时，两端母线侧故障电流和差比值与电流各个频点复频率以及两侧系统阻抗和故障位置均有关系。

3 基于模型识别的保护原理研究

上文分别推导出了区外和区内故障时的故障特征模型，当线路不同位置发生故障时，均应符合相应的特征模型。模型识别的基本思想是：构造一个模型误差函数，用于量化故障数据与模型的符合程度，通过计算比较模型误差函数值来识别出故障符合的特征模型，进而判断故障发生的位置。

例如，已知m侧区外故障特征模型为Hm（s），假设由故障数据计算得到的电流和差比值为h（s），m侧区外故障模型误差函数可以定义为：

当发生m侧区外故障时，故障数据符合m侧区外特征模型，此时Em=0；当发生m侧区内故障或者n侧区外故障时，故障数据不符合m侧区外特征模型，则Em≠0。据此，可以判断出是否发生m侧区外故障。同理，可以构造m侧区内以及n侧区外故障模型误差函数，来进行故障位置的判断。

本文区内故障特征模型待定参数较多，求解比较复杂，因此只采用两侧区外故障特征模型。区外故障特征模型与两侧系统阻抗有关，只有给定两侧系统阻抗，Hm（s）和 Hn（s）才能确定下来。 而两侧系统阻抗受系统运行方式影响不断变化，不能离线给定，只能在线实时计算，本文给出一种利用故障电流工频量求解系统阻抗的方法，然后构造两侧区外故障模型误差函数，最后给出保护判据。

3.1 系统阻抗求解

对于n侧区外故障，将工频频点和差电流比值h（s0）代入式（12），可反解出m侧系统阻抗的表达式：

其中，γ0、d、l1、l2为已知；s0=j ω0，ω0为同步角频率；h（s0）= [ΔIm（s0）+ΔIn（s0）]/[ΔIm（s0）-ΔIn（s0）]可由矩阵束计算得到。

同理，可以推导出n侧系统阻抗的计算表达式为：

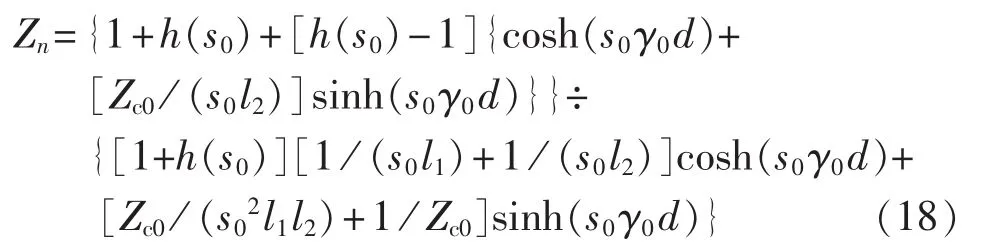
两侧系统阻抗求出后，可确定两侧区外故障特征模型的形式，即得电流模型识别保护的基准模型。

3.2 保护判据的形成

电流模型识别保护基准模型确定以后，需要进一步构造模型误差函数识别出基准模型，从而判断出故障发生的位置。式（16）给出了一种模型误差函数构造方法，本文在其基础上，给出一种利用不平衡电流描述故障数据与基准模型符合程度的模型误差函数构造方法。以m侧区外故障为例，特征模型误差函数具体求解步骤如下。

a.求解模型在每个频点的不平衡电流ΔIN（si）。由式（16）可以得到：

其中，h（si）为由矩阵束计算得到的m侧区外故障实际模型值；Hm（si）为m侧区外故障模型在第i个频点处的理论值。 令 ΔI+（si）=ΔIm（si）+ΔIn（si），ΔI-（si）=ΔIm（si）-ΔIn（si），则有：

定义m侧区外模型在第i个频点处不平衡电流：

b.求解各个频点模型总不平衡电流。

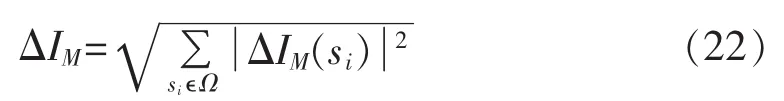
其中，Ω为各次谐波的集合。

c.构造模型误差函数Em。将m侧故障模型总不平衡电流与暂态总电流之比作为m侧区外故障的模型误差函数。故障暂态总电流为：

所以得到m侧区外故障模型误差函数为：

同理，可以得到n侧区外故障模型误差函数为：

理论上，当发生区外故障时，故障电流应该满足该侧区外故障特征模型，与其对应的模型误差函数应该为0，其不满足另一侧区外故障特征模型，所以另一侧故障模型误差函数不为0。当发生区内故障时，两侧区外故障模型均不满足，所以两侧区外故障模型误差函数均不为0。据此，给出适用于带并联电抗器输电线路的模型识别保护的判据如下。

区内故障：En＞ξ，且 Em＞ξ。

区外故障：En＜ξ，或 Em＜ξ。

ξ为判据动作门槛，按照躲过区外故障时，模型误差最大不平衡量整定。

4 仿真验证

分别采用ATP仿真软件和动模数据验证保护新原理的性能。

4.1 ATP仿真验证

利用ATP软件搭建400 km、750 kV单相输电线路模型见图3，两端并联电抗器补偿度均为0.7，线路采用分布参数模型，具体参数为：Em=750∠0°kV，Zm=102.94 Ω；r=0.01958 Ω /km，l=0.8192 mH /km，c=0.0135 μF /km；r0=0.1828 Ω /km，l0=2.74 mH /km，c0=0.0092 μF/km；En=750∠-30°kV，Zn=72.06 Ω；系统运行功角为30°，故障电流采样频率为10kHz，数据窗长为10 ms，采用最小二乘矩阵束算法提取故障电流暂态分量特征量，保护判据门槛值ξ=0.3。模型设置了5个故障点，分别为m侧区外故障点F1、n侧区外故障点F2、线路始端故障点F3、线路中点故障点F4、线路末端故障点F5。具体仿真结果如图4—8所示。

图3 ATP仿真系统模型图Fig.3 Model of ATP simulation system

图4为m侧区外故障时模型误差计算波形，m侧区外特征模型误差函数值Em均在动作门槛值ξ以下，而n侧区外模型误差函数值En均在动作门槛值以上，说明故障数据符合m侧区外故障模型，不符合n侧区外故障模型，可以准确地判断出故障发生在m侧区外，保护不会动作。图5为n侧区外故障时模型误差计算波形，同理可以准确判断出故障发生在n侧区外，保护仍然不会误动。

图4 m侧区外F1处故障时模型误差计算波形Fig.4 Calculation error of model when out-zone fault occurs at F1，m side

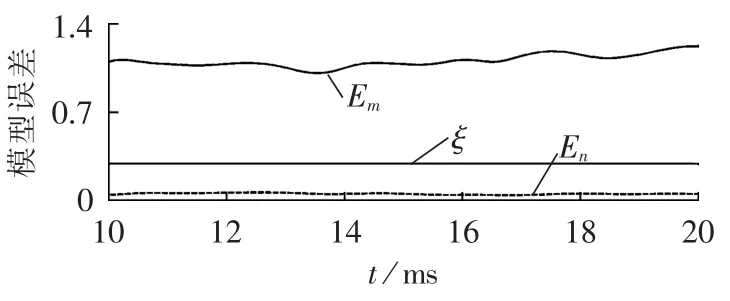
图5 n侧区外F2处故障时模型误差计算波形Fig.5 Calculation error of model when out-zone fault occurs at F2，n side

图6 线路始端F3处故障时模型误差计算波形Fig.6 Calculation error of model when fault occurs at F3，start point of line

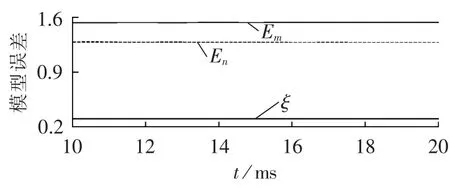
图7 线路中点F4处故障时模型误差计算波形Fig.7 Calculation error of model when fault occurs at F4，middle point of line

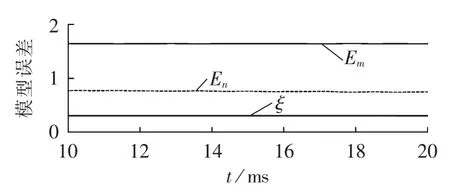
图8 线路末端F5处故障时模型误差计算波形Fig.8 Calculation error of model when fault occurs at F5，end point of line

图6为线路始端故障时模型误差计算波形，两侧区外故障模型误差函数值Em和En均大于动作门槛值ξ，说明故障均不符合两侧区外故障模型，可以准确判断出故障发生在区内，保护可靠动作。图7和图8分别为线路中间和末端故障时模型误差计算波形，与始端故障类似，Em和En均大于动作门槛ξ，可以准确判断出故障发生在区内。

4.2 动模仿真验证

采用中国电科院兰州东至咸阳750 kV线路动模实验数据，系统接线图与图3类似，m侧对应兰州东变电站，n侧对应咸阳变电站。线路长度为497 km，电流互感器变比为2000 A/1A。具体测试结果如图9—13所示。

对于m侧区外发生BC两相金属性接地故障，利用BC线模量计算出的模型误差波形如图9所示，m侧区外模型误差Em均小于动作门槛ξ，n侧区外模型误差En均大于动作门槛ξ，可以判定出故障发生在m侧区外。

图9 m侧区外BC两相金属性接地故障模型误差计算波形Fig.9 Calculation error of model when out-zone grounding fault of both phase B and phase C occurs at m side

图10 m侧区外BC两相相间故障模型误差计算波形Fig.10 Calculation error of model when out-zone interphase fault of phase B and C occurs at m side

图11 线路始端A相接地故障模型误差计算波形Fig.11 Calculation error of model when phase-A grounding fault occurs at start point of line

图12 线路1/4处三相故障模型误差计算波形Fig.12 Calculation error of model when three-phase fault occurs at 1/4 point of line

图13 线路3/4处B相经400 Ω过渡电阻接地时模型误差计算波形Fig.13 Calculation error of model when phase-B grounding fault via 400 Ω transition resistance occurs at 3/4 point of line

对于m侧区外BC相间金属性故障，利用BC线模量计算得到的模型误差波形如图10所示，与图9类似，可以判定故障发生在m侧区外。

对于线路始端A相金属性接地故障，利用AB线模量计算得到的模型误差波形如图11所示，两侧区外模型误差Em和En均在动作门槛值以上，说明故障均不符合两侧区外特征模型，判定出故障发生在区内，保护可靠动作。同理，对于图12线路1/4处三相故障以及图13线路3/4处经高阻接地故障，均可以准确判定故障发生在区内。

以上ATP软件和动模仿真结果表明，考虑并联电抗器的电流模型识别保护具有优良的性能，能够准确判断出故障发生在区内还是区外。

5 结论

本文针对两端带并联电抗器的输电线路提出了一种基于电流模型识别的保护新原理，通过理论分析和仿真验证可以得到以下结论：

a.电流模型识别保护新原理适用于带并联电抗器的输电线路，能够准确地判断出故障发生在区内还是区外，动作可靠；

b.该新原理不受线路分布电容的影响，无需补偿电容电流，具有一定的抗过渡电阻能力。

c.只采用双端电流量，不引入电压量，可靠性高；

d.采用10 ms的短数据窗，动作迅速。