并网型级联H桥变换器直流电压平衡和功率均衡控制策略

孙毅超，赵剑锋，季振东

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

近年来，随着智能电网中柔性交流输电技术应用的不断推进，电力电子装置在高压大功率场合获得了越来越普遍的应用；同时，由于IGBT等器件耐压水平的制约，多电平技术[1]已成为电力电子装置应用于高压大功率场合的核心技术。

级联型H桥变换器源于多电平技术，与箝位二极管和箝位电容式拓扑结构相比，它具有结构简单、易于模块化实现、可冗余运行等多种优点，因此，级联型结构成为高压大功率电力电子装置中的主流[2-5]，广泛应用于静止同步补偿器、光伏并网逆变器、电力电子变压器等实用场合。

各个H桥直流侧电压的建立需要网侧提供一定的有功功率，且该有功功率大小受到其自身损耗的影响，另外，在光伏并网逆变器、电力电子变压器等工况中，各H桥直流侧都能够向网侧提供或者从网侧获得一定的有功功率。因此，各H桥流经的有功功率不可能完全一致，甚至差别较大，而在传统控制下，有功功率差异正是引起各个H桥直流侧电压不平衡的根本原因。文献[6-9]针对链式静止同步补偿器工况提出了相应的直流侧电压平衡算法，文献[10-11]针对级联型电力电子变压器工况提出了相应的电压平衡控制算法。

目前，国内外学者主要侧重于对并网型级联型H桥变换器直流侧电压平衡的研究，并提出了若干种可行的控制策略[6-16]。这些方法的基本思想是通过增加一个电压平衡环节来实现各个H桥直流侧电压的平衡。然而，这些控制方法仅以直流侧电压为控制目标，必然会引起各个H桥无功功率的分配不均，在负载不平衡度大以及无功补偿任务重等情况下可能无法正常工作。

针对级联型H桥的功率平衡，研究主要集中在逆变器情况下调制方法的改进或是通过后级电路进行控制[10，17]，文献[18]以功率平衡为目标提出相应控制算法，但并不能保证各个H桥直流侧电压平衡，只能在特定场合下使用。

本文提出了一种基于调制波矢量重构技术的级联型H桥变换器电压平衡以及功率均衡的控制策略，在保证各个H桥直流侧电压平衡的基础上，使得有功功率按需分配、无功功率等量分配，同时分析讨论了该控制算法的约束条件，并通过仿真验证了算法的正确性与有效性，与已有方法相比适用于更大负载不平衡度工况。

1 数学模型

1.1 拓扑结构及矢量分析

级联型H桥变换器的拓扑结构如图1所示，忽略交流电感L内阻，用R等效各个H桥的自身损耗以及传输的有功功率。

系统稳态运行时网侧矢量图如图2所示，该工况下，变换器从电网吸收有功功率，向电网提供感性无功功率。文中采用粗体表示变量的矢量形式，非粗体表示其标量形式，由图可得如下数学模型：

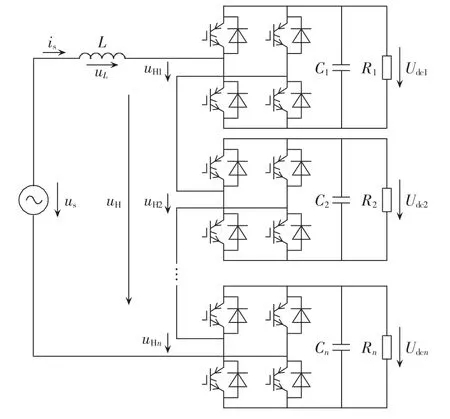
图1 级联型H桥变换器拓扑结构Fig.1 Topological structure of cascaded H-bridge converters

其中，UHd和UHq分别为变换器交流侧电压UH在网侧电流Is轴及其垂直轴上的投影，也可称为UH的有功分量和无功分量。

图2 网侧稳态运行矢量图Fig.2 Steady-state vector diagram of AC side

电网提供的视在功率为：

其中，负号表示无功功率由变换器向电网提供，下同。

各个H桥输入的视在功率为：

忽略H桥的自身损耗，则各个H桥输出的视在功率为：

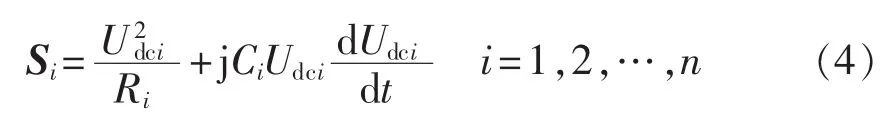
1.2 直流电压及功率不平衡机理

根据 H 桥线性调制理论[8，19]可得：

其中，Di为第i个H桥的调制波矢量。

由式（3）—（5）可得：

其中，Did为第i个H桥的调制波矢量在网侧电流轴上的有功分量。

由式（6）可知，若采用传统的双闭环控制策略，即D保持不变，此时D1d=D2d=…=Dnd，则：

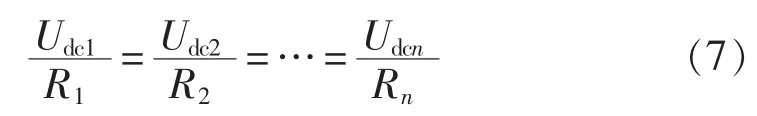
由式（7）可知，在R不完全相等时，各H桥直流侧电压无法保持平衡，且功率不能均衡，如图3所示，R越大，Udc越大，P和Q越大。图3中，电流矢量Is用标幺值I*s表示，则电流轴与其垂直轴分别可以表示有功和无功功率。

图3 仅双闭环控制下稳态矢量图Fig.3 Steady-state vector diagram under double closed loop control

若采用直接修改调制比的方法[9-13]，即Udc保持不变，此时 Udc1=Udc2=…=Udcn，则：

其中，mi为各个H桥调制比的修正系数，并且m1+m2+…+mn=0，即保证总功率守恒。

由式（8）可知，通过各个H桥的调制比修正系数mi匹配它们之间的负载差异，直流侧电压能达到平衡，但功率仍然不能均衡，如图4所示，R越大，mi越小，Udc不变，P和Q越小。

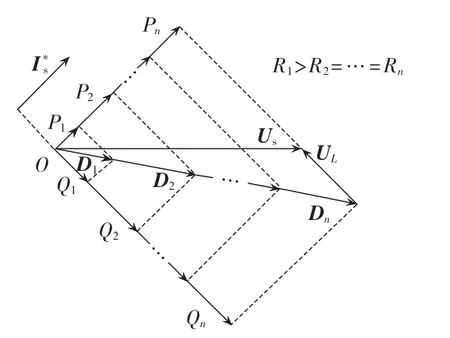
图4 电压平衡控制下稳态矢量图Fig.4 Steady-state vector diagram under DC voltage balance control

2 调制波矢量重构机理

2.1 直流电压平衡及功率均衡方法

本文在电压平衡控制的基础上，为使各个H桥无功功率均衡分配，引入了调制波矢量误差分量，将其叠加到原调制波矢量中，得到改进后的调制信号，如图5所示。

图5 电压平衡及功率均衡控制下稳态矢量图Fig.5 Steady-state vector diagram under DC voltage balance and power equilibrium control

图5 中，ΔDi（i=1，2，…，n）为调制波矢量误差分量，与电流矢量Is垂直；D′i为重构后的调制波矢量，则：

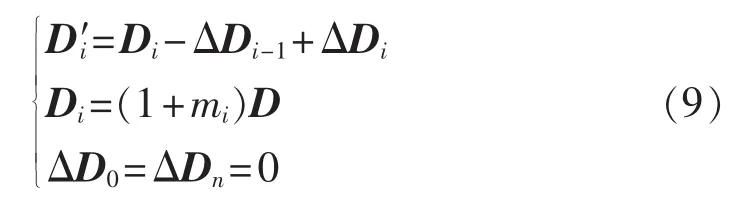
由递推公式（9）可求得各个H桥的重构调制波矢量，其中误差分量的计算如图6所示。

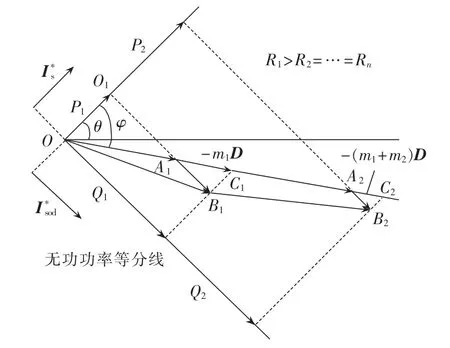
图6 均衡控制稳态矢量图局部放大图Fig.6 Partial enlarged steady-state vector diagram under equilibrium control

图6中△OO1A1与△C1B1A1、△C2B2A2互为相似三角形，因此∠A1C1B1=∠A2C2B2=φ，则：

其中，i=1，2，…，n；dm为未加平衡控制算法时的调制比，即D的幅值。

由式（8）—（10）可得各个H桥的重构调制波矢量计算公式为：

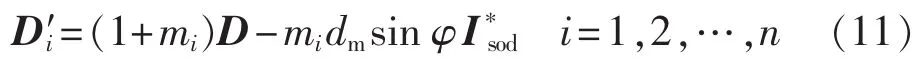
其中，I*sod为滞后I*s90°的单位矢量。

2.2 约束条件

根据线性调制理论[19]，可得计算式（11）的约束条件为，代入式（11）可得：

根据式（12）可作出其函数图如图7所示。

图7 重构调制比-修正系数函数图Fig.7 Reconstruction of modulation ratio-correction factor function

由式（12）可解得：

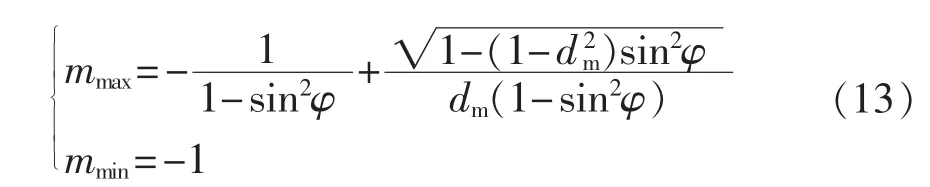
结合式（8）和（13）可得：

若设R1为基准负载，则R1/Ri可以表示为各个H桥的负载比，ηi可以表示为第i个H桥的负载不平衡度，ε2表示约束范围，因此式（14）具体反映了各个H桥之间负载差异的约束条件。

采用直接修改调制比方式的电压平衡控制方法时，根据式（8）可得该方式下的约束范围ε1=mmax+1=1/dm，其与本文提出的功率均衡控制方法的对比如图8所示，在功率均衡控制下，负载不平衡度的约束范围更宽，适用于更大负载差异的应用场合。

图8 2种控制方法约束范围对比图Fig.8 Comparison of restraint areas between two control schemes

3 控制策略

基于计算式（11），本文描述的级联型H桥变换器控制策略主要由双闭环控制、电压平衡控制以及功率均衡控制3个部分组成，如图9所示。

图9 级联型H桥电压平衡及功率均衡控制策略Fig.9 Control scheme of DC voltage balance and power equilibrium for cascaded H-bridge converters

双闭环控制由传统的双PI控制构成，电压外环稳定H桥直流侧电压均值，并形成有功电流指令，无功电流指令为外部给定；电流环采用电压前馈式控制，有效提高了系统的动态响应。

电压平衡控制为直接修改调制比方式，任意一个H桥直流侧电压受到各个H桥直流电压的影响[8]，因此每个H桥直流侧电压与直流侧电压均值比较后经过独立的PI作用后形成调制比修正系数mi，通过mi消除各个H桥直流侧电压之间的差异。

功率均衡控制在以上控制的基础上，通过式（11）计算各个H桥的调制波矢量误差分量，分别得到重构调制波矢量。其中，sin（ωt+θ）由Is经锁相环后得到；sin φ由Is与d亦经锁相环后得到。

4 仿真研究

为验证所提电压平衡和功率均衡控制策略的有效性，在MATLAB/Simulink中搭建了3个单元级联型变换器及其控制系统，仿真系统主要参数为：输入电压峰值Usm=1500 V，直流电压Udci=1000V，基准负载R1=50 Ω，无功功率Q=-100 kvar，直流电容Ci=3000 μF，滤波电感 L=2 mH，开关频率 f=1 kHz。

本文调制环节采用载波移相调制策略，能够利用较低的开关频率实现较高的等效开关频率，下文将分三部分分别验证本文所述的控制策略。

4.1 级联H桥直流电压平衡

基于式（8），通过直接修改各H桥调制比的方法使直流侧电压平衡，仿真时间为3 s，1 s时加入平衡控制，仿真结果如图10所示。如图10（a）所示，平衡后的直流侧电压波动各不相同，负载越重，纹波越大；各H桥的传输功率如图10（b）和10（c）所示，负载越重，有功及无功功率越大，与理论分析结果一致；3个H桥调制波仅调制比不同，如图10（d）所示。

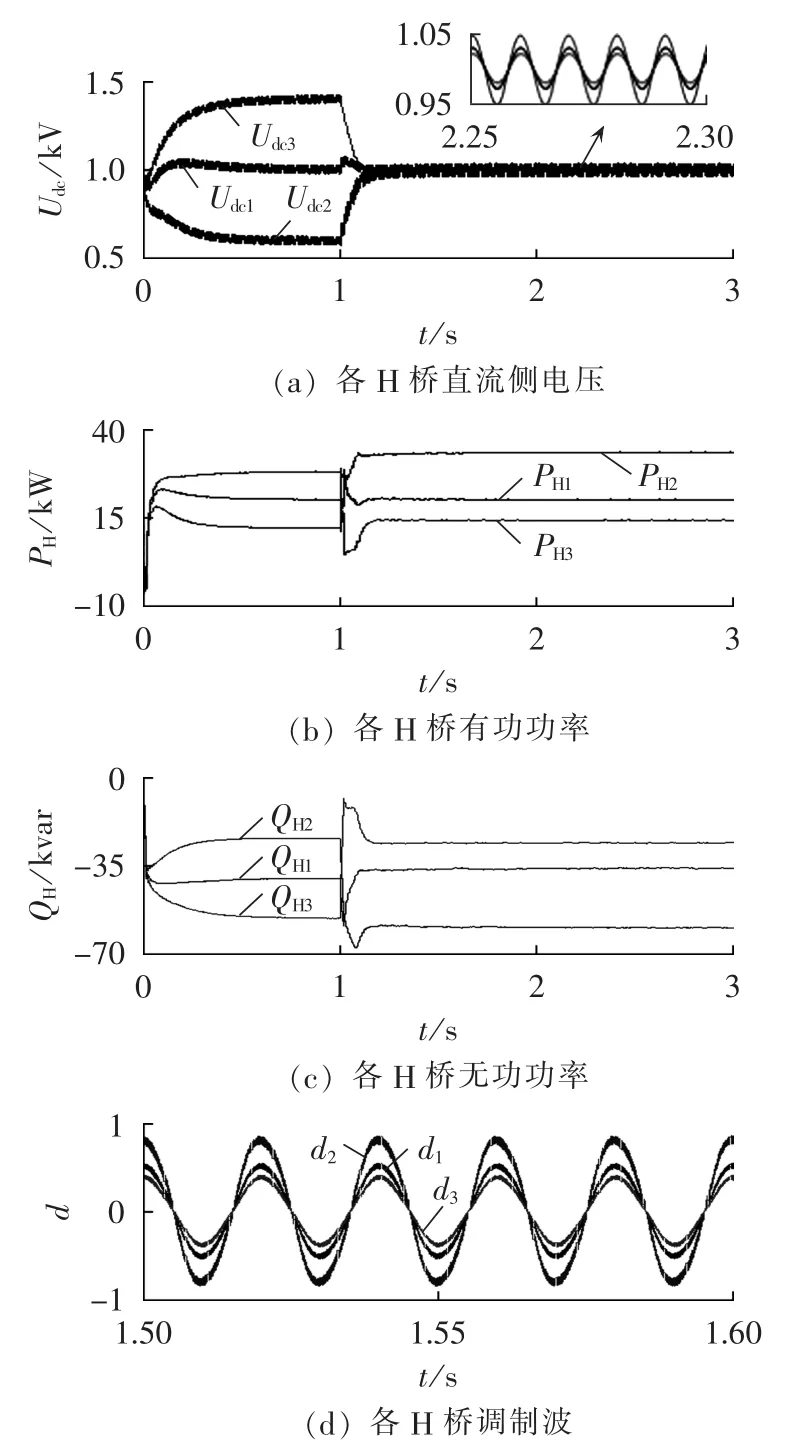
图10 电压平衡控制时波形Fig.10 Waveforms of DC voltage balance control

4.2 级联H桥功率均衡

基于本文提出的控制算法，仿真波形如图11所示，仿真时间为3 s，1 s时加入均衡控制。由图11（a）可知，各H桥直流侧电压纹波基本保持一致，与负载轻重无关；各H桥有功功率与图10（b）相同，按需分配，而无功功率趋于一致，各H桥平均分配网侧需要的无功，与负载轻重无关，如图 11（b）和11（c）所示；3个H桥调制波幅值与相位均不同，与理论分析一致，如图 11（d）所示。

4.3 负载不平衡的约束比较

取不平衡负载 R2=20 Ω、R3=180 Ω，由式（14）可计算负载的最大不平衡度ηmax=1.985，在本文仿真工况下，可计算出初始调制比dm=0.56，sin φ=0.85，根据图8可知，该负载不平衡度满足功率均衡下的约束条件，而不满足仅电压平衡时的约束条件。

仿真时间为3 s，1 s时加入电压平衡控制，2 s时加入功率均衡控制，如图12所示。

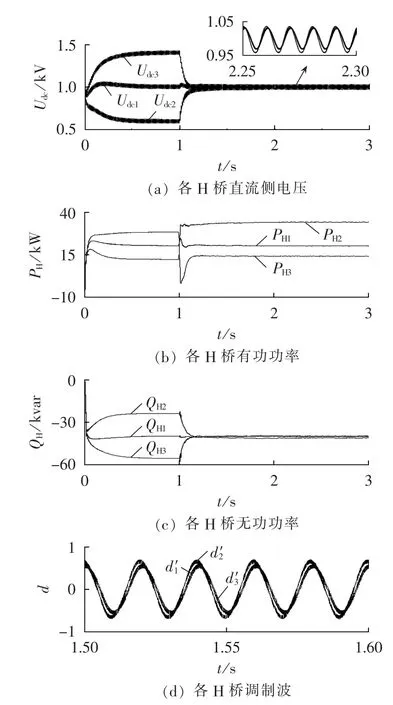
图11 电压平衡及功率均衡控制时波形Fig.11 Waveforms of DC voltage balance and power equilibrium control

由图12（a）可知，由于负载不平衡度超过了其约束条件，故仅电压平衡控制无法使直流侧电压仍然保持平衡，且各直流侧电压波动差别大；2 s加入功率均衡控制后，由于约束范围的扩大，使得负载不平衡度重新回到约束范围内，故直流侧电压仍然能保持平衡状态。

图12（b）和图 12（c）为功率变化图，同理，由于超出了电压平衡控制的约束范围，各H桥有功和无功功率均不满足与负载呈线性关系；2 s加入功率均衡控制后，有功功率重新按需分配，无功功率均衡分配。

图12（d）为加入功率均衡控制前后各H桥调制波波形，控制前d2明显超出了线性调制区的范围，且各调制波均已出现畸变；而均衡控制后，d2重新回到约束范围以内，保证了控制的有效性。

图12 大负载不平衡度下2种控制方法对比图Fig.12 Comparison of waveforms between two control schemes for large load unbalance

5 结论

本文提出了一种新的基于调制波矢量重构技术的级联型H桥变换器电压平衡及功率均衡控制方法，与直接修改调制比的电压平衡方法相比，该方法具有如下优点：

a.直流侧平衡电压纹波基本一致；

b.各H桥流经有功功率按需分配；

c.各H桥流经无功功率等量分配；

d.负载不平衡度的约束范围更宽，即线性调制范围更大，适用场合更广。